Методика быстрого счета в уме как называется: Устный счёт — Википедия – 5 методов для быстрого счёта в уме / TeachMePlease

Системы устного счета и их создатели

Уметь считать правильно и быстро – замечательная способность человеческого ума. Но далеко не все умеют ею пользоваться. Вместе с тем, счет в уме дает огромные преимущества. Нет, это не гонорар от выступлений на эстраде. Это уверенность во многих житейских ситуациях, не только связанных непосредственно с вычислениями, что само по себе очень полезно, но и психологическая уверенность.

Быстрый счет часто означает не интеллектуальную способность мозга, а умение применять на практике методики счета в уме, разработанные и описанные учеными — математиками. Для их освоения вовсе необязательно иметь выдающиеся математические способности, достаточно изучить эти методики по их книгам и активно применить в жизни.

В статье мы выделим гениальные книги – системы устного счета и их выдающихся создателей.

Яков Исидорович Перельман и его тридцать простых приемов устного счета

Надо отметить, что Яков Перельман (1882-1942) был выдающейся личностью. Наше поколение благодарно ему за то, что именно Перельман стал родоначальником жанра научно — занимательной литературы. Это сегодня принято обо всем рассказывать популярно, весело и доходчиво. А во времена Перельмана научная литература сильно отличалась от популярной.

Перельман написал более ста книг, которые и сегодня любимы взрослыми и детьми. Эти книги содержат по-настоящему ценные знания в разных областях, они способствуют развитию творческого подхода к точным наукам и раскрывают прекрасный мир математики, физики, астрономии. Это великолепные книги «Занимательная астрономия», «Занимательная алгебра», «Занимательная геометрия», «Занимательная физика» и другие.

Книги переведены на двадцать четыре языка. На обратной стороне Луны в честь этого удивительного человека назван кратер.

Книга Я. Перельмана «Быстрый счет. Тридцать простых приемов устного счета» содержит полезные и эффективные способы быстрого счета в уме. Они рассчитаны на способности обычного человека. Но если вы успешно освоите эти методы, вряд ли вас будут продолжать считать обычным человеком.

Яков Трахтенберг и его система быстрого счета

Хотите с удивительной скоростью не только складывать и умножать числа, но и извлекать корни и возводить в квадрат? Тогда вам нужно освоить систему замечательного цюрихского профессора, уроженца Одессы Якова Трахтенберга (1888-1953).

Яков Трахтенберг окончил Петербургский горный институт. С 1919 года Яков проживал в Германии, позже переехал в Австрию.

В послевоенные годы Трахтенберг создал в Цюрихе математический институт и возглавил его.

Кроме математической деятельности Яков Трахтенберг известен как автор уникального авторского метода изучения иностранных языков.

Система Я. Трахтенберга направлена на тренировку скорости вычислений. Если вы сможете уделить системе значительное количество времени для выполнения упражнений, то скорость счета возрастет во много раз! Это удивительный метод, в корне отличающийся от стандартного изучения устного счета в школе.

Методика счета в уме Якова Трахтенберга описана в книге Энн Катлер и Рудольфа Мак-Шейна «Система быстрого счета по Трахтенбергу».

Сергей Александрович Рачинский  и его 1001 задача для умственных вычислений

Профессор ботаники МГУ С.А. Рачинский (1833-1902) предпочел должность сельского учителя в Смоленской губернии. За время своей педагогической деятельности, Рачинский накопил огромный опыт, нашедший отражение в труде «1001 задача для умственных вычислений». Это задачник по математическим вычислениям, впервые увидевший свет в Санкт- Петербурге в 1891 году.

Учеником Сергея Рачинского был художник Н.П. Богданов-Бельский, увековечивший память об учителе известным полотном «Устный счет», находящимся сегодня в Третьяковской галерее. О картине подробнее вы можете прочитать здесь.

Прочитать о жизни С. А. Рачинского, о его системе счета подробнее можно в книге «Сельский учитель С.А. Рачинский и его задачи для умственных вычислений» И.И. Баврина.

 

Отложите калькулятор. Возможно, пришло время считать по-настоящему, используя свой ум, то есть по-человечески!

Владеете ли вы навыками устного счета? Какие книги по устному счету вам знакомы? Были ли ситуации, когда умение считать в уме вам очень помогло? Или неумение считать вас подводило? Поделитесь с нами!

Автор: Светлана Каминская (пользователь Камлана)

Методика «быстрого» счета

Отработка вычислительных навыков обучающихся на уроках математики с помощью приемов «быстрого» счета.

Кудинова И.К., учитель математики

МКОУ Лимановской СОШ

Панинского муниципального района

Воронежской области

«Приходилось ли тебе наблюдать, как люди с природными способностями к счёту бывают восприимчивы, можно сказать, ко всем наукам? Даже все те, кто туго соображает, если они обучаются этому и упражняются, то хотя бы они не извлекали из этого для себя никакой пользы, всё же становятся более восприимчивы, чем были раньше»

Платон

Важнейшей задачей образования является формирование универсальных учебных действий, обеспечивающих школьникам умение учиться, способность к саморазвитию и самосовершенствованию. Качество усвоения знаний определяется многообразием и характером видов универсальных действий. Формирование способности и готовности учащихся реализовывать универсальные учебные действия позволяет повысить эффективность процесса обучения. Все виды универсальных учебных действий рассматриваются в контексте содержания конкретных учебных предметов.

Важную роль в формировании универсальных учебных действий играет обучение школьников навыкам рациональных вычислений. Ни у кого не вызывает сомнения, что, развитие умения рациональных вычислений и преобразований, а также развитие навыков решения простейших задач «в уме» — важнейший элемент математической подготовки учащихся. Важность и необходимость таких упражнений доказывать не приходиться. Значение их велико в формировании вычислительных навыков, и совершенствовании знаний по нумерации, и в развитии личностных качеств ребенка. Создание определенной системы закрепления и повторения изученного материала дает учащимся возможность усвоения знаний на уровне автоматического навыка.

Знание упрощенных приемов устных вычислений остается необходимым даже при полной механизации всех наиболее трудоемких вычислительных процессов. Устные вычисления дают возможность не только быстро производить расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки. Кроме того, освоение вычислительных навыков развивает память и помогает школьникам полноценно усваивать предметы физико-математического цикла.

Очевидно, что приемы рационального счета  являются  необходимым элементом  вычислительной  культуры  в жизни каждого человека,  прежде всего силу своей практической значимости, а обучающимся она необходима практически на каждом уроке.

Вычислительная культура является фундаментом изучения математики и других учебных дисциплин, т. к. кроме того, что вычисления активизируют память, внимание, помогают рационально организовать деятельность и существенно влияют на развитие человека.

В повседневной жизни, на учебных занятиях, когда ценится каждая минута, очень важно  быстро и рационально провести устные и письменные вычисления, не допустив при этом ошибок и не используя при этом никаких дополнительных вычислительных средств.

Анализ результатов экзаменов в 9-х и 11-х классах показывает, что наибольшее количество ошибок учащиеся допускают при выполнении заданий на вычисления. Нередко даже высокомотивированные учащиеся к выходу на итоговую аттестацию утрачивают навыки устного счета. Они плохо и нерационально считают, все чаще прибегая к помощи технических средств-калькуляторов. Главная задача учителя – не только сохранить вычислительные навыки, но и научить применять нестандартные приемы устного счета, которые позволили бы значительно сократить время работы над заданием.

Рассмотрим конкретные примеры различных приемов быстрых рациональных вычислений.

РАЗЛИЧНЫЕ СПОСОБЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ

СЛОЖЕНИЕ

Основное правило для выполнения сложения в уме звучит так:

Чтобы прибавить к числу 9, прибавьте к нему 10 и отнимите 1;чтобы прибавить 8, прибавьте 10 и отнимите 2; чтобы прибавить 7, прибавьте10 и отнимите 3 и т.д. Например:

56+8=56+10-2=64;

65+9=65+10-1=74.

СЛОЖЕНИЕ В УМЕ ДВУЗНАЧНЫХ ЧИСЕЛ

Если цифра единиц в прибавляемом числе больше5, то число необходимо округлить в сторону увеличения, а затем вычесть ошибку округления из полученной суммы. Если же цифра единиц меньше, то прибавляем сначала десятки, а потом единицы. Например:

34+48=34+50-2=82;

27+31=27+30+1=58.

СЛОЖЕНИЕ ТРЕХЗНАЧНЫХ ЧИСЕЛ

Складываем слева на право, то есть сначала сотни, потом десятки, а затем единицы. Например:

359+523= 300+500+50+20+9+3=882;

456+298=400+200+50+90+6+8=754.

ВЫЧИТАНИЕ

Чтобы вычесть два числа в уме, нужно округлить вычитаемое, а затем подкорректируйте полученный ответ.

56-9=56-10+1=47;

436-87=436-100+13=349.

Умножение многозначных чисел на 9

1. Число десятков увеличим на 1 и вычтем из множимого

2. К результату приписываем дополнение цифры единиц множимого до 10

Пример:

576 · 9 = 5184 379 · 9 = 3411

576 – (57 + 1) = 576 – 58 = 518 . 379 – (37 + 1) = 341 .

4 1

Умножение на 99

1. Из числа вычитаем число его сотен, увеличенное на 1

2. Находим дополнение числа, образованного двумя последними цифрами до 100

3. Приписываем дополнение к предшествующему результату

Пример:

27 · 99 = 2673 (сотен – 0) 134 · 99 = 13266

27 – 1 = 26 134 – 2 = 132 (сотня – 1 + 1)

100 – 27 = 73 66

Умножение на 999 любого числа

1. Из умножаемого вычитаем число тысяч, увеличенное на 1

2. Находим дополнение до 1000

23 · 999 = 22977 ( тысяч – 0 + 1 = 1)

23 – 1 = 22

1000 – 23 = 977

124 · 999 = 123876 ( тысяч – 0 + 1 = 1)

124 – 1 = 123

1000 – 124 = 876

1324 · 999 = 1322676 (тысяча – 1 + 1 = 2)

1324 – 2 = 1322

1000 – 324 = 676

Умножение на 11, 22, 33, …99

Чтобы двузначное число, сумма цифр которого не превышает 10, умножить на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр:

72 ×11= 7 (7+2) 2 = 792;

35 ×11 = 3 (3+5) 5 = 385.

Чтобы умножить 11 на двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения:

94 ×11 = 9 (9+4) 4 = 9 (13) 4 = (9+1) 34 = 1034;

59×11 = 5 (5+9) 9 = 5 (14) 9 = (5+1) 49 = 649.

Чтобы двузначное число умножить на 22, 33. …99, надо последнее число представить в виде произведения однозначного числа (от 1 до 9) на 11, т.е.

44= 4 × 11; 55 = 5×11 и т. д.

Затем произведение первых чисел умножить на 11.

48 × 22 =48 × 2 × (22 : 2) = 96 × 11 =1056;

24 × 22 = 24 × 2 × 11 = 48 × 11 = 528;

23 ×33 = 23 × 3× 11 = 69 × 11 = 759;

18 × 44 = 18 × 4 × 11 = 72 × 11 = 792;

16 × 55 = 16 × 5 × 11 = 80 × 11 = 880;

16 × 66 = 16 × 6 × 11 = 96 × 11 = 1056;

14 × 77 = 14 × 7 × 11 = 98 × 11 = 1078;

12 × 88 = 12 × 8 × 11 = 96 × 11 = 1056;

8 × 99 = 8 × 9 × 11 = 72 × 11 = 792.

Кроме того, можно применить закон об одновременном увеличении в равное число раз одного сомножителя и уменьшении другого.

Умножение на число, оканчивающееся на 5

Чтобы четное двузначное число умножить на число, оканчивающееся на 5, следует применить правило: если один из сомножителей увеличить в несколько раз, а другой – уменьшить во столько же раз, произведение не изменится.

44 × 5 = (44 : 2) × 5 × 2 = 22 × 10 = 220;

28 × 15 = (28 : 2) × 15 × 2 = 14 × 30 = 420;

32 × 25 = (32 : 2) × 25 × 2 = 16 × 50 = 800;

26 × 35 = (26 : 2) × 35 × 2 = 13 × 70 = 910;

36 × 45 = (36 : 2) × 45 × 2 = 18 × 90 = 1625;

34 × 55 = (34 : 2) × 55 × 2 = 17 × 110 = 1870;

18 × 65 = (18 : 2) × 65 × 2 = 9 × 130 = 1170;

12 × 75 = (12 : 2) × 75 × 2 = 6 × 150 = 900;

14 × 85 = (14 : 2) × 85 × 2 = 7 × 170 = 1190;

12 × 95 = (12 : 2) × 95 × 2 = 6 × 190 = 1140.

При умножении на 65, 75, 85, 95 числа следует брать небольшие, в пределах второго десятка. В противном случае вычисления усложнятся.

Умножение и деление на 25, 50, 75, 125, 250, 500

Для того, чтобы устно научиться умножать и делить на 25 и 75, надо хорошо знать признак делимости и таблицу умножения на 4.

На 4 делятся те, и только те числа, у которых две последние цифры числа выражают число, делящееся на 4.

Например:

124 делится на 4, так как 24 делится на 4;

1716 делится на 4, так как 16 делится на 4;

1800 делится на 4, так как 00 делится на 4

Правило. Чтобы число умножить на 25, надо это число разделить на 4 и умножить на 100.

Примеры:

484 × 25 = (484 : 4) × 25 × 4 = 121 × 100 = 12100

124 × 25 = 124 : 4 × 100 = 3100

Правило. Чтобы число разделить на 25, надо это число разделить на 100 и умножить на 4.

Примеры:

12100 : 25 = 12100 : 100 × 4 = 484

31100 : 25 = 31100 :100 × 4 = 1244

Правило. Чтобы число умножить на 75, надо это число разделить на 4 и умножить на 300.

Примеры:

32 × 75 = (32 :4) × 75 × 4 = 8 × 300 = 2400

48 × 75 = 48 : 4 × 300 = 3600

Правило. Чтобы число разделить на 75, надо это число разделить на 300 и умножить на 4.

Примеры:

2400 : 75 = 2400 : 300 × 4 = 32

3600 : 75 = 3600 : 300 × 4 = 48

Правило. Чтобы число умножить на 50, надо это число разделить на 2 и умножить на 100.

Примеры:

432× 50 = 432 :2 × 50 × 2 = 216 × 100 = 21600

848 × 50 = 848 : 2 × 100 = 42400

Правило. Чтобы число разделить на 50, надо это число разделить на 100 и умножить на 2.

Примеры:

21600 : 50 = 21600 : 100 × 2 = 432

42400 : 50 = 42400 : 100 × 2 = 848

Правило. Чтобы число умножить на 500, надо это число разделить на 2 и умножить на 1000.

Примеры:

428 × 500 = (428 :2) × 500 × 2 = 214 × 1000 = 214000

2436 × 500 = 2436 : 2 × 1000 = 1218000

Правило. Чтобы число разделить на 500, надо это число разделить на 1000 и умножить на 2.

Примеры:

214000 : 500 = 214000 : 1000 × 2 = 428

1218000 : 500 = 1218000 : 1000 × 2 = 2436

Прежде чем научиться умножать и делить на 125, надо хорошо знать таблицу умножения на 8 и признак делимости на 8.

Признак. На 8 делятся те и только те числа, у которых три последние цифры выражают число, делящееся на 8.

Примеры:

3168 делится на 8, так как 168 делится на 8;

5248 делится на 8, так как 248 делится на 8;

12328 делится на 8, так как 324 делится на 8.

Чтобы узнать, делится ли трехзначное число, оканчивающееся цифрами 2, 4, 6. 8. на 8, нужно к числу десятков прибавить половину цифр единиц. Если полученный результат будет делиться на 8, то исходное число делится на 8.

Примеры:

632 : 8, так как т.е. 64 : 8;

712 : 8, так как т.е. 72 : 8;

304 : 8, так как т.е. 32 : 8;

376 : 8, так как т.е. 40 : 8;

208 : 8, так как т.е. 24 : 8.

Правило. Чтобы число умножить на 125, надо это число разделить на 8 и умножить на 1000. Чтобы число разделить на 125, надо это число разделить на 1000 и умножить

на 8.

Примеры:

32 × 125 = (32 : 8) × 125 × 8 = 4 × 1000 = 4000;

72 × 125 = 72 : 8 × 1000 = 9000;

4000 : 125 = 4000 : 1000 × 8 = 32;

9000 : 125 = 9000 : 1000 × 8 = 72.

Правило. Чтобы число умножить на 250, надо это число разделить на 4 и умножить на 1000.

Примеры:

36 × 250 = (36 : 4) × 250 × 4 = 9 × 1000 = 9000;

44 × 250 = 44 : 4 × 1000 = 11000.

Правило. Чтобы число разделить на 250, надо это число разделить на 1000 и умножить на 4.

Примеры:

9000 : 250 = 9000 : 1000 ×4 = 36;

11000 : 250 = 11000 : 1000 ×4 = 44

Умножение и деление на 37

Прежде чем научиться устно умножать и делить на 37, надо хорошо знать таблицу умножения на три и признак делимости на три, который изучается в школьном курсе.

Правило. Чтобы умножить число на 37, надо это число разделить на 3 и умножить на 111.

Примеры:

24 × 37 = (24 : 3) × 37 × 3 = 8 × 111 = 888;

27 × 37 = (27 : 3) × 111 = 999.

Правило. Чтобы число разделить на 37, надо это число разделить на 111 и умножить на 3

Примеры:

999 : 37 = 999 :111 × 3 = 27;

888 : 37 = 888 :111 × 3 = 24.

Умножение на 111

Научившись умножать на 11, легко умножить на 111, 1111. и т. д. число, сумма цифр которого меньше 10.

Примеры:

24 × 111 = 2 (2+4) (2+4) 4 = 2664;

36 ×111 = 3 (3+6) (3+6) 6 = 3996;

17 × 1111 = 1 (1+7) (1+7) (1+7) 7 = 18887.

Вывод. Чтобы число умножить на 11, 111. и т. д., надо мысленно цифры этого числа раздвинуть на два, три и т. д. шагов, сложить цифры и записать между раздвинутыми цифрами.

Умножение двух рядом стоящих чисел

Примеры:

1) 12 ×13 = ? 1 × 1 = 1 1 × (2+3) = 5 2 × 3 = 6 156 2) 23 × 24 = ? 2 × 2 = 4 2 × (3+4) = 14 3 × 4 = 12 552 3) 32 × 33 = ? 3 × 3 = 9 3 × (2+3) = 15 2 × 3 = 6 1056 4) 75 × 76 = ? 7 × 7 = 49 7 × (5+6) = 77 5 × 6 = 30 5700

Проверка: ×12 13 36 12_ 156 Проверка: × 23 24 92 46_ 552 Проверка: × 32 33 96 96_ 1056 Проверка: × 75 76 450 525_ 5700

Вывод. При умножении двух рядом стоящих чисел надо сначала перемножить цифры десятков, затем цифру десятков умножить на сумму цифр единиц и, наконец, надо перемножить цифры единиц. Получим ответ (см. примеры)

Умножение пары чисел, у которых цифры десятков одинаковые, а сумма цифр единиц составляет 10

Пример:

24 × 26 = (24 – 4) × (26 + 4) + 4 × 6 = 20 × 30 + 24 = 624.

Числа 24 и 26 округляем до десятков, чтобы получить число сотен, и к числу сотен прибавляем произведение единиц.

18 × 12 = 2 × 1 сот. + 8 × 2 = 200 + 16 = 216;

16 × 14 = 2 × 1 × 100 + 6 × 4 = 200 + 24 = 224;

23 × 27 = 2 × 3 × 100 + 3 × 7 = 621;

34 × 36 = 3 × 4 сот. + 4 × 6 = 1224;

71 × 79 = 7 × 8 сот. + 1 × 9 = 5609;

82 × 88 = 8 × 9 сот. + 2 × 8 = 7216.

Можно решать устно и более сложные примеры:

108 × 102 = 10 × 11 сот. + 8 × 2 = 11016;

204 × 206 = 20 × 21 сот. +4 × 6 = 42024;

802 × 808 = 80 × 81 сот. +2 × 8 = 648016.

Проверка:

× 802

808

6416

6416__

648016

Умножение двузначных чисел, у которых сумма цифр десятков равна 10, а цифры единиц одинаковые.

Правило. При умножении двузначных чисел. у которых сумма цифр десятков равна 10, а цифры единиц одинаковые, надо перемножить цифры десятков. и прибавить цифру единиц, получим число сотен и к числу сотен прибавим произведение единиц.

Примеры:

72 × 32 = (7 × 3 + 2)сот. + 2 × 2 = 2304;

64 × 44 = (6 × 4 + 4) × 100 + 4 × 4 = 2816;

53 × 53 = (5 × 5 +3) × 100 + 3 × 3 = 2809;

18 × 98 = (1 × 9 + 8) × 100 + 8 × 8 = 1764;

24 × 84 = (2 × 8 + 4) ×100+ 4 × 4 = 2016;

63 × 43 = (6 × 4 +3) × 100 +3 × 3 = 2709;

35 × 75 = (3 × 7 + 5) × 100 +5 × 5 = 2625.

Умножение чисел, оканчивающихся на 1

Правило. При умножении чисел, оканчивающихся на 1, надо сначала перемножить цифры десятков и правее полученного произведения записать под этим числом сумму цифр десятков, а затем перемножить 1 на 1 и записать еще правее. Сложив столбиком, получим ответ.

Примеры:

1) 81 × 31 = ? 8 × 3 = 24 8 + 3 = 11 1 × 1 = 1 2511 81 × 31 = 2511

2) 21 × 31 = ? 2 × 3 = 6 2 +3 = 5 1 × 1 = 1 651 21 × 31 = 651

3) 91 × 71 = ? 9 × 7 = 63 9 + 7 = 16 1 × 1 = 1 6461 91 × 71 = 6461

Умножение двузначных чисел на 101, трехзначных – на 1001

Правило. Чтобы двузначное число умножить на 101, надо к этому числу приписать справа это же число.

Примеры: 32 × 101 = 3232

Проверка: × 32 101 32 32__ 3232

48 × 101 = 4848;

56 × 101 = 5656.

Правило. Чтобы трехзначное число умножить на 1001, надо к этому числу справа приписать это же число.

Примеры:

324 1001 = 324324

Проверка: 324 1001 324 324___ 324324

648 1001 = 648648;

999 1001 = 999999.

Приемы устных рациональных вычислений, используемые на уроках математики, способствуют повышению общего уровня математического развития;  развивают у учеников навык быстро выделять из известных им законов, формул, теорем те, которые следует применить для решения предложенных задач, расчетов и вычислений; содействуют развитию памяти, развивают способность зрительного восприятия математических фактов, совершенствуют пространственное воображение. 

Помимо этого, рациональный счет на уроках математики играет немаловажную роль в повышении у детей познавательного интереса к урокам математики, как одного из важнейших мотивов учебно-познавательной деятельности, развития личностных качеств ребенка. Формируя навыки устных рациональных вычислений, учитель тем самым воспитывает у учащихся навыки сознательного усвоения изучаемого материала, приучает ценить и экономить время, развивает желание поиска рациональных путей решения задачи. Иными словами формируются познавательные, включая логические, познавательные и знаково-символические универсальные учебные действия.

Цели и задачи школы кардинально меняются, осуществляется переход от знаниевой парадигмы к лично-ориентированному обучению. Потому важно не просто учить решать задачи по математике, а показывать действие основных математических законов в жизни, объяснять, как может учащийся применить полученные знания. И тогда у детей появится главное: желание и смысл учиться.

Список литературы

Минских Е.М. «От игры к знаниям», М., «Просвещение» 1982.

Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986.

Совайленко ВК. Система обучения математике в 5-6 классах. Из опыта работы.- М.:Просвещение, 1991.

Катлер Э. Мак-Шейн Р. «Система быстрого счёта по Трахтенбергу» — М. Просвещение, 1967.

Хэндли Билл «Считать в уме как калькулятор» — Минск, Попурри, 2006.

Минаева С.С. «Вычисления на уроках и внеклассных занятиях по математике.» — М.: Просвещение, 1983. 

Сорокин А.С. «Техника счета (методы рациональных вычислений)», М, Знани», 1976

http://razvivajka.ru/ Тренировка устного счета

http://gzomrepus.ru/exercises/production/ Упражнения на продуктивность и быстрый устный счет

Быстрый счёт (Перельман) — Викитека

[2]От составителя

В настоящее время в продаже нет
 руководств, содержащих наставления к
 быстрому выполнению счетных операций
 в уме. Мы сочли поэтому полезным собрать в краткой брошюре наиболее простые и легко усваиваемые приемы быстрого устного счета. Они рассчитаны на
 средние способности и имеют в виду не
 публичные выступления на эстраде, а
 потребности повседневной жизни. Пользующиеся книжечкой должны помнить, что успешное овладение ее указаниями
 предполагает не механическое, а вполне
 сознательное распоряжение приемами
 и, кроме того, более или менее продолжительную тренировку. Зато, усвоив
 рекомендуемые приемы, можно выполнять быстрые расчеты в уме с безошибочностью письменных вычислений.

Отв. редактор В. А. Камский. Техн. ред. А. Я. Барвиш

---

М 18609

1/4 печ. листа. Тираж 5 000.

4-я тип. Лениздата им. Григорьева 4021 [3]Умножение на однозначное число

§ 1. Чтобы устно умножить число на
 однозначный множитель (например, 27 × 8),
 выполняют действие, начиная с умножения
 не единиц, как при письменном умножении, а иначе: умножают сначала десятки множимого (20 × 8 = 160), затем единицы
 (7 × 8 = 56) и оба результата складывают.

Еще примеры:

34 × 7 = 30 × 7 + 4 × 7 = 210 + 28 = 238

47 × 6 = 40 × 6 + 7 × 6 = 240 + 42 = 282


§ 2. Полезно знать на память таблицу
 умножения до 19 × 9:

	2	3	4	5	6	7	8	9
11	22	33	44	55	66	77	88	99
12	24	36	48	60	72	84	96	108
13	26	39	52	65	78	91	104	117
14	28	42	56	70	84	98	112	126
15	30	45	60	75	90	105	120	135
16	32	48	64	80	96	112	128	144
17	34	51	68	85	102	119	136	153
18	36	54	72	90	108	126	144	162
19	38	57	76	95	114	133	152	171

Зная эту таблицу, можно умножение
 например, 147 × 8 выполнить в уме так:


147 × 8 = 140 × 8 + 7 × 8 = 1120 + 56 = 1176


§ 3. Когда одно из умножаемых чисел
 разлагается на однозначные множители,
 удобно бывает последовательно умножать
 на эти множители. Например:

225 × 6 = 225 × 2 × 3 = 450 × 3 = 1350 [4]Умножение на двузначное число

§ 4. Умножение на двузначное число
 стараются облегчить для устного выполнения, приводя это действие к более привычному умножению на однозначное число.

Когда множимое однозначное, мысленно переставляют множители и выполняют
 действие, как указано в § 1. Например:

6 × 28 = 28 × 6 = 120 + 48 = 168

§ 5. Если оба множителя двузначные,
 мысленно разбивают один из них на десятки и единицы. Например:

29 × 12 = 29 × 10 + 29 × 2 = 290 + 58 = 348 41 × 16 = 41 × 10 + 41 × 6 = 410 + 246 = 656 (или 41 × 16 = 16 × 41 = 16 × 40 + 16 =
 640 + 16 = 656)

Разбивать на десятки и единицы выгоднее тот множитель, в котором они выражены меньшими числами.

§ 6. Если множимое или множитель
 легко разложить в уме на однозначные
 числа (напр., 14 = 2 × 7), то пользуются
 этим, чтобы уменьшить один из множителей, увеличив другой во столько же раз
 (ср. § 3). Например:

45 × 14 = 90 × 7 = 630 [5]Умножение на 4 и на 8

§ 7. Чтобы устно умножить число на
 4, его дважды удваивают. Например:

112 × 4 = 224 × 2 = 448
 335 × 4 = 670 × 2 = 1340

§ 8. Чтобы устно умножить число на
 8, его трижды удваивают. Например:

217 × 8 = 434 × 4 = 868 × 2 = 1736

(Еще удобнее: 217 × 8 = 200 × 8 +
 17 × 8 = 1600 × 13 = 1736).

Деление на 4 и на 8

§ 9. Чтобы устно разделить число на
 4, его дважды делят пополам. Например:

76 : 4 = 38 : 2 = 19
 236 : 4 = 118 : 2 = 59

§ 10. Чтобы устно разделить число на
 8, его трижды делят пополам. Например:

464 : 8 = 232 : 4 = 116 : 2 = 58
 516 : 8 = 258 : 4 = 129 : 2 = 64¹/₂ [6]Умножение на 5 и на 25

§ 11. Чтобы устно умножить число на
 5, умножают его на 10/2, т. е. приписывают к числу ноль и делят пополам. Например:

74 × 5 = 740 : 2 = 370
 243 × 5 = 2430 : 2 = 1215

При умножении на 5 числа четного
 удобнее сначала делить пополам и к полученному приписать ноль. Например:

74 × 5 = 74/2 × 10 = 370

§ 12. Чтобы устно умножить число на 25, умножают его на 100/4, т. е. — если число кратно 4-х — делят на 4 и к частному приписывают два ноля. Например:

72 × 25 = 72/4 × 100 = 1800

Если же число при делении на 4 дает
 остаток, то

при	приписывают
остатке:	к частному
1	25
2	50
3	75

Основание приема ясно из того, что


100 : 4 = 25; 200 : 4 = 50; 300 : 4 = 75 [7]Умножение на 1¹/₂, на 1¹/₄, на 2¹/₂, на ³/₄

§ 13. Чтобы устно умножить число на
 1¹/₂ прибавляют к множимому его половину. Например:

34 × 1¹/₂ = 34 + 17 = 51
 23 × 1¹/₂ = 23 + 11¹/₂ = 34¹/₂ (или 34,5)

§ 14. Чтобы устно умножить число на
 1¹/₄, прибавляют к множимому его четверть. Например:

48 × 1¹/₄ = 48 + 12 = 60
 58 × 1¹/₄ = 58 + 14¹/₂ = 72¹/₂ или (72,5)

§ 15. Чтобы устно умножить число на
 2¹/₂, к удвоенному числу прибавляют половину множимого. Например:

18 × 2¹/₂ = 36 + 9 = 45
 39 × 2¹/₂ = 78 + 19¹/₂ = 97¹/₂ (или 97,5)


Другой способ состоит в умножении
 на 5 и делении пополам:

18 × 2¹/₂ = 90 : 2 = 45

§ 16. Чтобы устно умножить число на
 ³/₄ (т. е. чтобы найти ³/₄ этого числа),
 умножают число на 1¹/₂ и делят пополам.
 Например:

30 × ³/₄ = 30 + 15/2 = 22¹/₂ (или 22,5) Видоизменение способа состоит в том, что
 от множимого отнимают его четверть или
 к половине множимого прибавляют половину этой половины. [8]Умножение на 15, на 125, на 75

§ 17. Умножение на 15 заменяют умножением на 10 и на 1¹/₂ (потому что
 10 × 1¹/₂ = 15). Например:

18 × 15 = 18 × 1¹/₂ × 10 = 270
 45 × 15 = 450 + 225 = 675

§ 18. Умножение на 125 заменяют умножением на 100 и на 1¹/₄ (потому что
 100 × 1¹/₄ = 125). Например:

26 × 125 = 26 × 100 × 1¹/₄ = 2600 + 650 = 3250 47 × 125 = 47 × 100 × 1¹/₄ = 4700 + 4700/4 = 4700 + 1175 = 5875

§ 19. Умножение на 75 заменяют умножением на 100 и на ³/₄ (потому что
 100 × ³/₄ = 75). Например:

18 × 75 = 18 × 100 × ³/₄ = 1800 × ³/₄ = 1800 + 900/2 = 1350

‎Примечание. Некоторые из
 приведенных примеров удобно выполняются также приемом § 6:

18 × 15 = 90 × 3 = 270
 26 × 125 = 130 × 25 = 3250 [9]Умножение на 9 и на 11

§ 20. Чтобы устно умножить число на
 9, приписывают к нему ноль и отнимают
 множимое. Например:

62 × 9 = 620 — 62 = 600 — 42 = 558
 73 × 9 = 730 — 73 = 700 — 43 = 657

§ 21. Чтобы устно умножить число на
 11, приписывают к нему ноль и прибавляют множимое. Например:

87 × 11 = 870 + 87 = 957 Деление на 5, на 1¹/₂, на 15

§ 22. Чтобы устно разделить число на
 5, отделяют запятой в удвоенном числе последнюю цифру. Например:

68 : 5 = 136/10 = 13,6
 237 : 5 = 474/10 = 47,4

§ 23. Чтобы устно разделить число на
 1¹/₂, делят удвоенное число на 3. Например:


36 : 1¹/₂ = 72 : 3 = 24
 53 : 1¹/₂ = 106 : 3 = 35¹/₃

§ 24. Чтобы устно разделить число на
 15, делят удвоенное число на 30. Например:


240 : 15 = 480 : 30 = 48 : 3 = 16
 462 : 15 = 924 : 30 = 3024/30 = 30⁴/₅ = 30,8
 (или 924 : 30 = 308 : 10 = 30,8) [10]Возвышение в квадрат

§ 25. Чтобы возвысить в квадрат число, оканчивающееся цифрой 5 (например
 85), умножают число десятков (8) на него
 же плюс единица (8 × 9 = 72) и приписывают 25 (в нашем примере получается 7225).
 Еще примеры:

25²; 2 × 3 = 6; 625

 45²; 4 × 5 = 20; 2025

 145²; 14 × 15 = 210; 21025


Прием этот вытекает из формулы


(10x + 5)² = 100x² + 100x + 25 = 100x (x + 1) + 25


§ 26. Сейчас указанный прием приложим и к десятичным дробям, оканчивающимся цифрой 5:

8,5² = 72,25 14,5² = 210,25

 0,35² = 0,1225, и т. п.

§27. Так как 0,5 = ¹/₂, а 0,25 = ¹/₄, то
 приемом §25 можно пользоваться также и
 для возвышения в квадрат чисел, оканчивающихся дробью ¹/₂:

(8¹/₂)² = 72¹/₄ (14¹/₂)² = 210¹/₄ и т. п.

§ 28. При устном возвышении в квадрат часто удобно бывает пользоваться формулой (а ± b)² = а² + b² ± 2аb. Например:


41² = 40² + 1 + 2 × 40 = 1601 + 80 = 1681
 69² = 70² + 1 — 2 × 70 = 4901 — 140 = 4761
 36² = (35 + 1)² = 1225 + 1 + 2 × 35 = 1296
 Прием удобен для чисел, оканчивающихся на 1, 4, 6 и 9.
[11]Вычисления по формуле (а + b) (а — b) = а² — b²

§ 29. Пусть требуется выполнить устно умножение

52 × 48

‎Мысленно представляем эти множители в
 виде (50 + 2) × (50 — 2) и применяем приведенную в заголовке
 формулу:

(50 + 2) × (50 — 2) = 50² — 2² = 2496

‎Подобным же образом поступают во всех
 вообще случаях, когда один множитель
 удобно представить в виде суммы двух
 чисел, другой — в виде разности тех же
 чисел:

69 × 71 = (70 — 1) × (70 + 1) = 4899
 33 × 27 = (30 + 3) × (30 — 3) = 891
 53 × 57 = (55 — 2) × (55 + 2) = 3021
 84 × 86 = (85 — 1) × (85 + 1) = 7224

§ 30. Указанным сейчас приемом удобно
 пользоваться и для вычислений следующего
 рода:

7¹/₂ × 6¹/₂ = (7 + ¹/₂) × (7 — ¹/₂) = 48³/₄ 11³/₄ × 12¹/₄ = (12 — ¹/₄) × (12 + ¹/₄) = 14315/16 [12]Полезно запомнить:


Запомнив это, легко выполнять устно
 умножение числа 37 на 6, 9, 12 и т. п.

37 × 6 = 37 × 3 × 2 = 222
 37 × 9 = 37 × 3 × 3 = 333
 37 × 12 = 37 × 3 × 4 = 444
 37 × 15 = 37 × 3 × 5 = 555 и т. д.

‎Запомнив это, легко выполнять устно умножения следующего рода:

77 × 13 = 1001	91 × 11 = 1001
77 × 26 = 2002	91 × 22 = 2002
77 × 39 = 3003	91 × 33 = 3003
и т. д.	и т. д.

143 × 7 = 1001
 143 × 14 = 2002
 143 × 21 = 3003
 и т. д.

---

---

В нашей книжечке указаны только
 простейшие, наиболее удобоприменимые
 способы устного выполнения действий
 умножения, деления и возвышения в квадрат. Практикуясь в сознательном пользовании ими, вдумчивый читатель выработает для себя ряд еще и других приемов,
 облегчающих вычислительную работу.
[13]УКАЗАТЕЛЬ Умножение

на однозначное число  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§§  1— 3

на двузначное число  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§§  4— 6

разности на сумму  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§§ 29—30

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 16—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 14—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 13—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 15—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§  7—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 11—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§  8—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 20—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 21—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 17—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 12—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 19—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 18—00

Деление

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 23—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§  9—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 22—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 10—00

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§ 24—00

Возвышение в квадрат  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

§§ 25—28

---

Как научиться быстро считать в уме ℹ️ техника быстрого счета любых чисел в уме, приемы и способы для взрослых и детей, правила и примеры

Нюансы, которые следует учитывать

Чтобы научиться умножать двузначные числа или складывать дроби, придется потратить достаточно много времени. Однако для более быстрого обучения важно концентрировать внимание на трех основных моментах, без которых время будет потрачено впустую:

1. Концентрация внимания. Процесс обучения будет куда более эффективным, если математик научится фокусировать свое внимание на той задаче, которую выполняет, ведь очень часто приходится отвлекаться на различные внешние факторы, которые не позволяют быстро посчитать или сложить в уме сложные числа. Чтобы такого не происходило, важно научиться концентрироваться на выполнении лишь одной задачи за один раз. Для этого стоит найти для место, где никто не будет мешать, а также постараться отбросить все мысли о работе, личной жизни, планах на будущее и прочем.
2. Формулы. Чтобы производить вычисление даже сложных математических уравнений в уме, придется запомнить основные формулы и теоремы, по которым это можно сделать. Само собой, чтобы найти неизвестную переменную, иногда можно использовать и банальный метод подбора, однако такой способ является гораздо более сложным. Поэтому важно выучить всю теоретическую информацию, которую можно будет использовать: формулу дискриминанта, теорему Виета и прочие математические хитрости, с помощью которых процесс счета упрощается в несколько раз.
3. Практика. Как бы это парадоксально ни звучало, но чтобы освоить технику быстрого счета в уме, необходимо для начала научиться выполнять те же задачи на листке бумаги. Ведь записывая выполнение того или иного упражнения, можно всегда посмотреть, где именно была совершена ошибка в процессе тренировки и сделать кое-какие выводы. Как только арифметик научится легко решать сложные примеры в тетради, самое время переходить на устный счет.

Как только все правила и теоремы будут запомнены, а человек научится не только решать сложные задачи на листке бумаги, но и концентрировать свое внимание, можно приступать к процессу обучения устному счету. Под каждое математическое действие существует свой особый прием и даже несколько тренажеров, позволяющих освоить технику гораздо быстрее.

Вот и польза от интернета

Чтобы научить ребенка считать в уме, можно скачать ему на телефон специальное приложение, в котором есть огромное количество различных примеров, на решение которых дается от 2 до 5 секунд. Само собой, можно попытаться составить уравнения и задачи самому, однако практика показывает, что в большинстве случаев они получаются крайне однообразными и не несут большой пользы. Также существуют специальные сайты, которые позволяют своим посетителям решать уравнение и сложные задачки в режиме онлайн. Используя такие платформы, самое главное — подобрать под себя правильный уровень сложности.

Чтобы система обучения приносила как можно большую пользу, важно понять, что вовсе не обязательно часами сидеть за примерами или пытаться решить сложные задачи сразу в уме. Ментальный счет — это долгий и кропотливый процесс, который не терпит спешки, и чтобы учиться правильно, достаточно уделять примерам от 5 до 10 минут в день. В противном случае голова будет напрягаться, а ученик начнет совершать глупейшие ошибки. Со временем даже такое «микрообучение» приведет к потрясающим результатам. Нужно лишь набраться терпения и практиковаться согласно рекомендациям математиков.

Сложение двузначных и трехзначных чисел

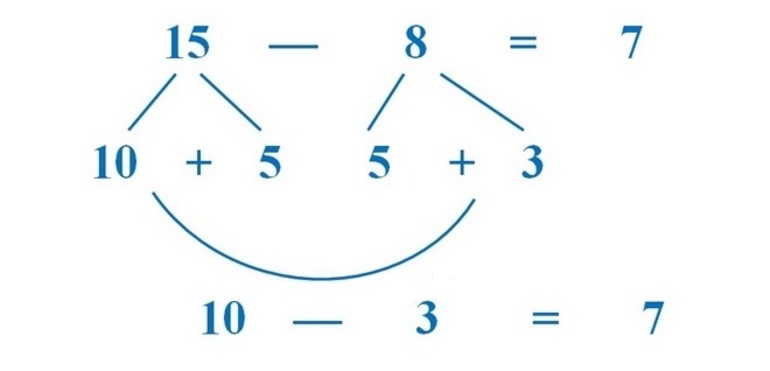
Как в первом классе детей учили быстро складывать и вычитать в уме однозначные числа? Правильно, позволяли для этого использовать пальцы. Ну а умножение и деление были освоены благодаря специальной таблице. Однако большинство взрослых, решивших научиться быстро считать в уме любые числа, как правило, умеют проводить эти действия не только с однозначными, но и с двузначными числами. В этом случае практиковаться будет значительно легче.

Однако если подросток не может сложить два двузначных числа, то сначала придется освоить именно эту методику, ведь от нее все и отталкивается. Как это сделать? Достаточно просто разбить двузначное число на десятки и единицы. То есть если перед учеником стоит пример 65+18, то необходимо каждое число сначала разложить: 65=60+5, 18=10+8. После этого складываем в уме десятки, а уже потом единицы: 60+10=70, 5+18=13. Если в процессе получается еще одно двузначное число, которое будет всегда состоять из одного десятка, то достаточно лишь прибавить сначала его, а уже потом — все имеющиеся единицы: 70+10=80, 80+3=83. Все довольно просто.

Однако когда речь заходит о трехзначных числах, то большинство людей почему-то сразу же входят в ступор, хотя методика здесь практически ничем не отличается от той, которая уже известна. Для начала необходимо разбить основное число на сотни, десятки и единицы, после чего начать складывать их между собой. Вот небольшой пример: 528+376. Действовать нужно по тому же алгоритму, что и ранее:

• Разбить числа: 528=500+20+8, 376=300+70+6.
• Сложить сотни: 500+300=800.
• Сложить десятки: 20+70=90.
• Сложить единицы 6+8=14.
• Сплюсовать все, что есть: 800+90+10+4=800+100+4=900+4=904.

Иногда, складывая десятки, также может получаться число больше сотни. Пугаться в этом случае не стоит. Достаточно будет просто прибавить одну сотню к уже имеющимся, после чего проводить арифметические действия с оставшимися десятками. Самое главное — не ошибиться в процессе.

Особенности вычитания

В математике существует всего два «полноправных» действия — сложение и умножение. Вычитание и деление являются обратными от этих двух. Кроме того, их всегда можно заменить умножением, подставив число «x», или сложением, подставив знак минус к неизвестному слагаемому. Именно поэтому, чтобы научиться вычитанию, сперва необходимо научиться складывать числа. Ведь в любой момент можно просто поменять в уме переменные и проверить правильность решения с помощью «x». Методика вычитания трехзначных чисел практически ничем не отличается от сложения. Вот небольшой пример: 553−192, а также подробный разбор:

• Разбить имеющиеся числа на сотни, десятки и единицы: 500=500+50+3, 192=100+90+2.
• Провести вычитание с сотнями: 500−100=400.
• Вычесть десятки, заняв одну сотню: 150−90=60.
• Вычесть единицы: 3−2=1.
• Сложить остатки, не забыв о заемных сотнях или десятках: «300+60+1=361».

То есть даже в вычитании будет обязательно присутствовать сложение. Основная сложность расчета таких примеров заключается в постоянной необходимости занимать десятки. Однако если проводить такую тренировку ежедневно, то со временем считать трехзначные числа будет ненамного сложнее, чем двухзначные. Самое главное — верить в себя и собственные силы.

Секреты умножения

Вот человеку нужно посчитать, находясь возле кассы, сколько же будет стоить 4 килограмма клубники по 183 рубля. Для этого он вытаскивает из кармана телефон и долго ищет в меню калькулятор. Однако куда быстрее будет посчитать все в уме. Самое главное — знать методику, которая позволяет это делать максимально правильно, а также как можно больше практиковаться. Алгоритм действий выглядит следующим образом.

• Разложить основное число, как и в случае с умножением: 183=100+80+3.
• Умножить число 4 на каждое имеющееся слагаемое: 100*4=400, 80*4=8*4*10=32*10=320, 3*4=12.
• Сложить все имеющиеся числа: 400+320+12=700+32=732.

Ничего сложного в этом нет, не говоря уже о том, что в умножении существует довольно много приемов, позволяющих провести операцию гораздо быстрее. К примеру, если человеку необходимо умножить какое-то число на 25, то достаточно просто разделить его на 4, после чего умножить на 100. Вот небольшой пример: 400*25=400/4*100=100*100=10000. Почему именно 4 и 100? Просто число 25 было замещено десятичной дробью ¼, ведь 25 — это 1 часть из 4 у сотни. Так что подобным приемом можно пользоваться, если необходимо быстро умножить что-то на «четвертак».

Сложности деления

Деление — самое сложное арифметическое действие, которое крайне трудно совершать в уме. Однако существует одна методика, которая является практически беспроигрышной. Как уже говорилось ранее, деление не является самостоятельным действием, поскольку оно обратное от умножения. Ведь что такое 32:8? Правильно: «x*8=32». Ну а по таблице умножения всем хорошо известно, что вместо переменной необходимо поставить число 4. Таким приемом можно пользоваться и для того, чтобы научиться быстро считать в уме.

Взрослому человеку это не составит большого труда, а вот ребенку придется сперва познакомиться с тем, что такое неизвестные переменные и как их искать.

Если человек научился проводить умножение с трехзначными числами в уме, то ему не составит особого труда для того, чтобы разделить эти числа. Вот небольшой пример: 795:3. Казалось бы, что посчитать его крайне трудно, но, чтобы упростить задачу, можно разбить его на множители, а также ввести переменные:

• Разбить число 795 на слагаемые, с которыми легко провести деление: «795=600+195».
• Поделить число 600 на 3 и держим в уме ответ: 200.
• Разделить число 195 на 3, но здесь необходимо также разделить его на слагаемые: 195=150+45.
• Поделить крупное число на 3: 150:3=50 и прибавляем ответ к имеющемуся: 200+50=250.
• Не зная таблицы деления, ввести переменную «x» для оставшегося числа 45=x*3. Получается, что x=15.
• Сложить остатки и проверить ответ умножением: 250+15=265, 265*3=200*3+60*3+5*3=795″ — все сходится.

Таким образом, чтобы облегчить процесс деления, можно воспользоваться не только методом разложения числа на слагаемые, но и вводя новую переменную. Особенно полезным этот навык окажется для того, кто проводит математические действия с более интересным и сложными примерами. Несколько месяцев практики обязательно принесут плоды, но следует взять себе за привычку проверять решение не с помощью калькулятора, а умножения.

Высчитывание процентов

Многие люди впадают в ступор, когда их просят найди 6 процентов от 253. Однако если знать основные математические правила, то в этом нет абсолютно ничего сложного. Причем, чтобы научиться проводить все действия в уме, не потребуется нескольких лет практики. Достаточно лишь следовать определенному алгоритму действий:

• Найти 1% от имеющегося числа. Для этого его необходимо разделить на 100: «253:100=2,53».
• Разложить получившиеся число на слагаемые, которые будет легко умножить на 6: 2,53=2+0,5+0,03.
• Провести умножение: 2*6=12, 0,5*6=½*6=3, 0,03*6=0,18.
• Сложить получившиеся значения: 12+3+0,18=15+0,18=15,18.

Чтобы научиться считать числа в уме, вовсе не обязательно быть вундеркиндом или потратить годы практики. Достаточно просто знать основные правила и формулы, которые позволяют упростить те или иные действия, а также уметь грамотно заменить некоторые переменные. Ну и, пожалуй, важнее всего — концентрироваться на выполнении определенной задачи. Если решать такие примеры каждый день, то со временем от калькулятора можно будет отказаться вовсе, что очень удобно, ведь даже в век информационных технологий полностью положиться на машины нельзя.