что это, упражнения и задачи
Ментальная арифметика сегодня на пике популярности. В каждом городе появляются новые развивающие центры, в уже существующих создаются специальные курсы. Родители, которых интересует этот вопрос, уже наверняка видели детей, производящих в уме без калькулятора сложные математические действия. Однако всем ли подходит эта методика обучения и в чем ее особенности, знают единицы.
Что такое ментальная арифметика?
Ментальная арифметика – это методика, которая учит быстрому счету. По сути, это набор упражнений для тренировки и развития мозга в процессе мысленной визуализации арифметических действий на специальных счетах. Чтобы научиться пользоваться этими счетами в уме, необходимо запомнить расположение косточек на спицах, а также выучить все ключевые манипуляции с ними. Счеты абакус представляют собой рамку с перекладинами и шестью спицами, на каждой из которых по пять костяшек.
Интересно!
Корни ментальной арифметики уходят в Древний Китай, но сама новаторская методика была изобретена в Турции. Она призвана дать человеку понимание пространственности и состава числа, что является отличной базой для дальнейшего изучения математики.
Кому подходит эта методика обучения?
Обучиться ментальной арифметике могут все желающие, но лучше всего эта программа усваивается детьми от 4 до 12 лет, поскольку именно в этом возрасте развитие мозга происходит максимально интенсивно, а многие навыки, полученные в этот период, сохраняются на всю жизнь.
Не стоит думать, что дети, которые не имеют направленности на точные науки, не смогут освоить данную методику.
Занимаясь ментальной арифметикой, они смогут совершенствовать свои творческие способности, а также забыть про свою нелюбовь к цифрам. Гиперактивные дети научатся обуздывать свои порывы и станут более спокойными.
Справка!
Обучиться ментальной арифметике могут не только дети, но и взрослые.
Зачем?
В реальной жизни ментальная арифметика поможет:
- Направлять внимание на главное. Если послушать интервью успешных людей, можно понять, что прийти к заветной цели им помогли вера в свои силы, настойчивость и умение концентрироваться на одной задаче. Ментальная арифметика научит сосредотачивать внимание на одной задаче и за счет этого справляться с ней максимально быстро.
- Быстро принимать решения. Ежедневные тренировки прививают умение оперативно находить решение, поэтому тот, кто владеет методикой ментальной арифметики, в любой кризисной ситуации выберет то, что важно.
- Быть уверенным в себе. Когда домашние задания перестают быть тягостными и невыполнимыми, ребенок чувствует себя гораздо увереннее, у него закрепляется установка «я победитель», следовательно, он сможет справиться с любыми сложными задачами в своей жизни.
- Творчески подходить к решению вопросов. Во время занятий ментальной арифметикой развивается воображение, поэтому появляется навык нешаблонного мышления.
- Легко общаться. Так как ментальная арифметика развивает оба полушария мозга, центры, которые отвечают за общение и эмоции, тоже активизируются. Это способствует более легкому общению, умению сопереживать и делиться.
Основные подходы
Как уже понятно из названия методики, ее принцип основывается на развитии способности считать в уме.
Начальные занятия проводятся в легкой игровой форме, поэтому у ребенка не будет создаваться впечатление о сложности этой программы и развиваться неуверенность в собственных силах.
Методика заключается в преодолении 10 этапов, каждый из которых рассчитан в среднем на 3–4 месяца при занятиях не реже 2 раз в неделю.
Важно! Положительные изменения можно заметить уже через 2–3 месяца регулярных занятий.
Сначала примеры будут простыми, но в дальнейшем их сложность увеличивается. На первых этапах обучения дети будут использовать счеты, что способствует одновременному развитию обоих полушарий головного мозга.
Далее наступает этап обучения счету без специальных приспособлений.
Это помогает не только развитию воображения и умению обращаться с цифрами в уме, но способнос
что это, упражнения и задачи
Ментальная арифметика сегодня на пике популярности. В каждом городе появляются новые развивающие центры, в уже существующих создаются специальные курсы. Родители, которых интересует этот вопрос, уже наверняка видели детей, производящих в уме без калькулятора сложные математические действия. Однако всем ли подходит эта методика обучения и в чем ее особенности, знают единицы.
Что такое ментальная арифметика?
Ментальная арифметика – это методика, которая учит быстрому счету. По сути, это набор упражнений для тренировки и развития мозга в процессе мысленной визуализации арифметических действий на специальных счетах. Чтобы научиться пользоваться этими счетами в уме, необходимо запомнить расположение косточек на спицах, а также выучить все ключевые манипуляции с ними. Счеты абакус представляют собой рамку с перекладинами и шестью спицами, на каждой из которых по пять костяшек.
Интересно!
Корни ментальной арифметики уходят в Древний Китай, но сама новаторская методика была изобретена в Турции. Она призвана дать человеку понимание пространственности и состава числа, что является отличной базой для дальнейшего изучения математики.
Кому подходит эта методика обучения?
Обучиться ментальной арифметике могут все желающие, но лучше всего эта программа усваивается детьми от 4 до 12 лет, поскольку именно в этом возрасте развитие мозга происходит максимально интенсивно, а многие навыки, полученные в этот период, сохраняются на всю жизнь.
Не стоит думать, что дети, которые не имеют направленности на точные науки, не смогут освоить данную методику.
Занимаясь ментальной арифметикой, они смогут совершенствовать свои творческие способности, а также забыть про свою нелюбовь к цифрам. Гиперактивные дети научатся обуздывать свои порывы и станут более спокойными.
Справка!
Обучиться ментальной арифметике могут не только дети, но и взрослые.
Зачем?
В реальной жизни ментальная арифметика поможет:
- Направлять внимание на главное. Если послушать интервью успешных людей, можно понять, что прийти к заветной цели им помогли вера в свои силы, настойчивость и умение концентрироваться на одной задаче. Ментальная арифметика научит сосредотачивать внимание на одной задаче и за счет этого справляться с ней максимально быстро.
- Быстро принимать решения. Ежедневные тренировки прививают умение оперативно находить решение, поэтому тот, кто владеет методикой ментальной арифметики, в любой кризисной ситуации выберет то, что важно.
- Быть уверенным в себе. Когда домашние задания перестают быть тягостными и невыполнимыми, ребенок чувствует себя гораздо увереннее, у него закрепляется установка «я победитель», следовательно, он сможет справиться с любыми сложными задачами в своей жизни.
- Творчески подходить к решению вопросов. Во время занятий ментальной арифметикой развивается воображение, поэтому появляется навык нешаблонного мышления.
- Легко общаться. Так как ментальная арифметика развивает оба полушария мозга, центры, которые отвечают за общение и эмоции, тоже активизируются. Это способствует более легкому общению, умению сопереживать и делиться.
Основные подходы
Как уже понятно из названия методики, ее принцип основывается на развитии способности считать в уме.
Начальные занятия проводятся в легкой игровой форме, поэтому у ребенка не будет создаваться впечатление о сложности этой программы и развиваться неуверенность в собственных силах.
Методика заключается в преодолении 10 этапов, каждый из которых рассчитан в среднем на 3–4 месяца при занятиях не реже 2 раз в неделю.
Важно! Положительные изменения можно заметить уже через 2–3 месяца регулярных занятий.
Сначала примеры будут простыми, но в дальнейшем их сложность увеличивается. На первых этапах обучения дети будут использовать счеты, что способствует одновременному развитию обоих полушарий головного мозга.
Далее наступает этап обучения счету без специальных приспособлений.
Это помогает не только
Как считать на счетах | Блог 4brain

В данной статье вы прочитаете, как научиться правильно считать на русских счетах. Вероятно, многие молодые люди ни разу не видели живьем такой арифметический инструмент, как счеты. А кто и видел, скорее всего, не знает, что с помощью этого инструмента можно научиться быстро складывать, вычитать и даже умножать и делить достаточно большие числа. Конечно, сегодня это не так актуально. Но в рамках раздела, посвященного устному счету, думаю, многим будет интересно прочитать о таком популярном приспособлении, облегчающем устный счет, но не исключающим его полностью.
Описание
Знаменитые деревянные счеты, изображенные на рисунке ниже, повсеместно использовались в СССР первые две трети двадцатого века в основном для операций сложения и вычитания. Как же кассиры и бухгалтера пользовались этими русскими счетами? Давайте разберемся. Если же вы умеете пользоваться счетами, то можете перейти сразу к описанию более сложных операций.
В исходном положении в «обнуленных» счетах все костяшки выровнены по правому краю (как показано на рисунке). Каждый ряд костяшек представляет собой разряд числа, единицы находятся над четырьмя костяшками. Выше единиц – десятки, сотни и т.д., ниже – четверти, десятые и сотые. С таким раскладом удобно считать деньги, где в ходу есть четвертаки (например, 25 копеек). Черным цветом выделены центральные костяшки (для удобства).

Набор числа. Если мы хотим установить какое-нибудь число на счетах (для совершения с ним в дальнейшем арифметических действий), то необходимо просто передвинуть нужные костяшки налево. Например, для набора числа «3 251,5» передвигаем 2 четвертака (или 5 десятых), 1 единицу, 5 десяток, 2 сотни и 3 тысячи.

Но набор числа, это только начало. По-настоящему пользоваться деревянными счетами, значит совершать арифметические операции.
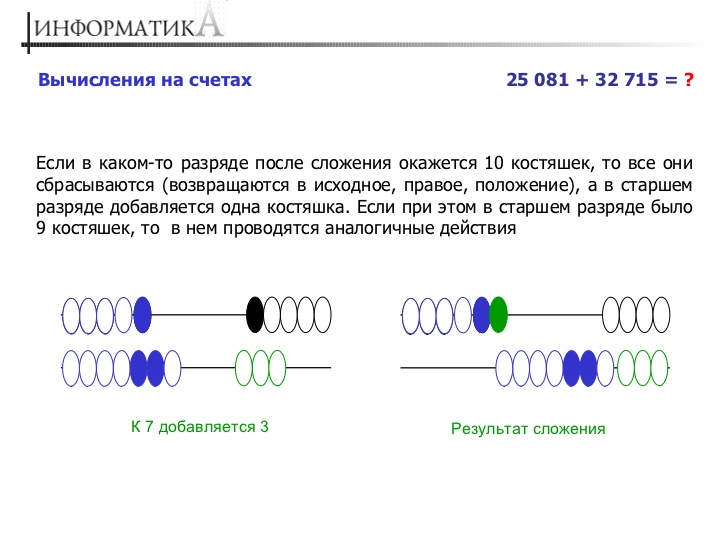
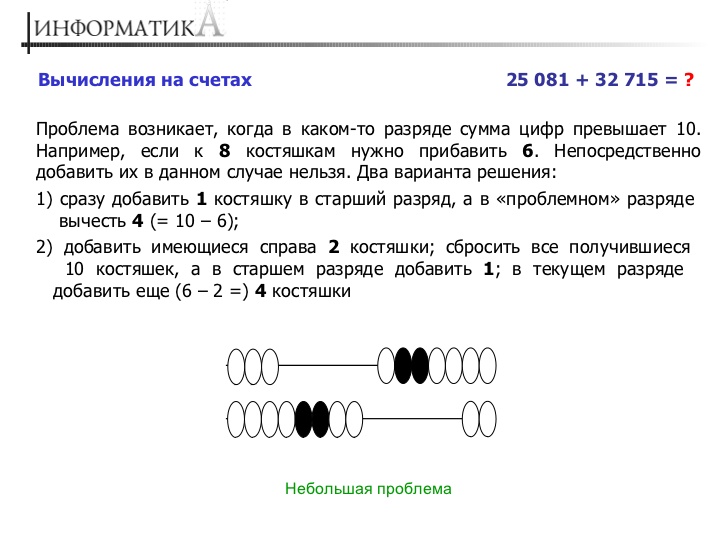
Сложение
Чтобы сложить на счетах два числа, нужно просто набрать костяшками одно число, а затем перенести налево каждый разряд второго числа, начиная с нижних рядов (именно с нижних!). Если вдруг выясняется, что костяшек в каком-то ряду не хватает, то в этом ряду нужно оставить столько костяшек, сколько не хватает, а на уровне выше перекинуть влево еще 1 костяшку. Чтобы лучше разобраться, как правильно складывать числа на счетах, смотрите пример ниже (987 + 134 = 1 121):

Вычитание
Вычитание на счетах производится точно таким же образом, как сложение, – сверху вниз. Только если костяшек в ряду не хватает, в этом ряду нужно оставить (10-x) костяшек, где x-число нехвативших костяшек, а в ряду выше нужно убрать одну костяшку (сдвинуть ее вправо). Ниже смотрите пример, как правильно считать разность на русских счетах (121 – 98 = 23):

Умножение
Умножение на счетах является не самым быстрым и простым. В некоторых случаях, гораздо проще воспользоваться навыками быстрого умножения в уме. Однако в рамках данной статьи приведены некоторые методики умножения на деревянных счетах. Для того, чтобы умножить число на 2 или на 3, нужно просто сложить данное число с собой (при умножении на 2), и повторить эту процедуру при умножении на 3. Умножение на 4 производится как умножение на 2 с последующим умножением на 2 полученного результата. Что касается умножения на 5, как вы можете убедиться из этого урока, оно равносильно делению на 2 и последующему умножению на 10. В этом случае, после деления на 2 вы просто переносите разряды (костяшки) на уровень выше. Умножение на большие числа осуществляется при помощи комбинации описанных методов.
Деление
Деление на русских счетах является достаточно сложной процедурой. Использовать для этого счеты иногда просто иррационально. Если пример удобный, допустим, необходимо разделить 280 на 2, тогда действительно, нужно просто из каждого ряда отодвинуть направо половину костяшек и тогда получится 140. Но иные примеры в большинстве своем требуют сложных алгоритмов и хорошего развития внимания и краткосрочной памяти.
Учебный проект по математике «Русские счёты» (5 класс)
Учебный проект
Русские счёты
Авторы: Ли Яна, Угрюмова Виктория, ученицы 5 «Б» класса
Руководитель: Плотникова Е.А.
Школа-интернат №15 ОАО «РЖД» г. Челябинска
В современном мире практически каждый день появляются новые гаджеты, приборы облегчающие жизнь и деятельность человека. Одним из таких приборов, прочно вошедших в жизнь человека ещё до нашего появления на свет, стал микрокалькулятор. О возможностях калькулятора знает каждый школьник и свободно с ним управляется. Калькулятор способен мгновенно произвести любые арифметические действия.
Возникает естественный вопрос: А какой прибор использовали до появления калькулятора? Как и когда он появился? Может ли он быть использован нами для выполнения различных вычислений? Интересно, а способствует ли он формированию навыка устных вычислений?
Ведь всем известно, что несмотря на скорость, точность и иные достоинства, калькулятор/компьютер разрушают навык устного счета.
У нас возник вопрос: действительно ли, русские счёты являются предшественниками микрокалькулятора в России и какова сфера их применения?
Приступая к работе над проектом, мы сформулировали цели и задачи предстоящей работы.
Цель исследования:
изучить историю появления, совершенствования русских счётов,
показать значимость их применения для упрощения вычислений,
научиться выполнять вычисления на счётах,
найти возможности для применения русских счётов в обучении математике
Задачи исследования:
исследовать, применяют ли школьники приемы быстрого счета;
изучение источников, в которых встречаются приёмы вычислений на русских счётах;
систематизировать изученный материал, выбрать самые интересные и доступные приемы вычислений на счётах;
изучить возможности русских счётов для формирования у школьников десятичного состава числа, его разрядов, для формирования вычислительных навыков.
Для начала мы изучили историю счёта и приборов для счёта.
Как вы думаете что люди использовали на заре человечества при необходимости считать предметы?
Самым первым прибором для счёта были пальцы, камешки, узелки на верёвках, зарубки на костях и палочках.
Затем, примерно в четвёртом веке до нашей эры учёный Абакус придумал первое счётное устройство, состоящее из глиняной пластинки с желобами, в которых раскладывались камни, представляющие числа. Один желобок изображал единицы, другой – десятки. Этот прибор назвали в честь его создателя – АБАК.
В средние века это устройство крестоносцы привезли из Азии в Европу, и учёные стали применять его для простейших математических операций. Вскоре с появлением бухгалтерской науки стало неудобным и несолидным носить глиняные пластинки и для счёта стали использовать разлинованные таблицы.
В странах Востока распространены китайский аналог абака — суаньпань и японский — соробан. Конструкции принципиально аналогичны, используют десятичную систему счисления, хотя японский вариант несколько экономичнее (в китайском, как и в русских счётах, используются «лишние» с точки зрения математики косточки). Для китайского и японского абака существует скрупулёзно разработанный набор алгоритмов, позволяющих механически (то есть не занимаясь дополнительными вычислениями в уме или на бумаге) выполнять все четыре арифметических действия и даже извлекать квадратные и кубические корни.
Японский соробан по сей день активно применяется, несмотря на повсеместное распространение электронных калькуляторов. В Японии использование соробана является элементом школьной программы обучения счёту в младших классах. Также в Японии и странах, имеющих значительную японскую диаспору, счёт на соробане популярен как вид развлечения или своеобразный спорт.
Долгое время считалось, что русские счеты ведут свое происхождение от китайского суаньпаня, и лишь в начале 50-х годов ленинградский ученый И.Г. Спасский убедительно показал оригинальное русское происхождение этого счетного прибора — у него, во-первых, горизонтальное расположение спиц с косточками и, во-вторых, для представления чисел использована десятичная (а не пятеричная) система счисления.
Десятичный строй счетов — довольно веское основание для того, чтобы признать временем возникновения этого прибора XVI век, когда десятичный принцип счисления был впервые применен в денежном деле России.
В 30-е годы XVI века московское правительство, возглавляемое Еленой Глинской, матерью малолетнего Ивана Грозного, провело денежную реформу, объединив московскую и новгородскую денежные системы. Московская деньга, составлявшая в то время 1/200 московского рубля, и ее половина — полушка — стали половиной и четвертью новой основной монетной единицы, которая получила название «копейки». Благодаря введению копейки рубль стал делиться на 100 основных единиц.
Счеты являются первым простейшим приспособлением для вычислений счета. Они прошли длительный путь эволюции, в котором можно выделить четыре стадии.
Русские счеты широко использовались при начальном обучении арифметике в качестве учебного пособия. Благодаря известному французскому математику Ж. Пон-селе, который познакомился со счетами, будучи военнопленным офицером наполеоновской армии в Саратове, аналогичный прибор под названием булье появился во французских школах, а затем и в некоторых других странах Европы.
Между тем Запад почти не знает счетов — вы не найдете их ни в одном магазине Европы, и только в начальных школах имеются огромные счеты — наглядное классное пособие при обучении нумерации.
Правда, на русских счетах нельзя производить всех тех действий, которые выполняются машинами. Нынешние счетные машины, конечно, оставляют далеко позади наши счеты. Но во многом — например, в сложении и вычитании — счеты могут соперничать со сложными приборами. Впрочем, в искусных руках умножение и деление также значительно ускоряются на счетах, если знать приемы выполнения этих действий.
Познакомимся с некоторыми из них.




Сами счеты появились в глубокой древности. И с тех пор принципиально не изменились. Только называются везде по-разному. Международное название «Абак». В Китае «суаньпань», в Японии «соробан», а в России русские счеты. Между собой они отличаются только количеством спиц и косточек на них. Сам же принцип работы одинаков.
Русские счеты, аналог римских, появились в начале XVI столетия. Их использовали и в коммерции, и в школе для обучения арифметике. Но в 60-х годах XX века русские счеты, из системы школьного образования исключили. Как устаревший метод.
Хорошо забытая старая система счета, как новая заработала в 1993 году в Азии. А сегодня более 5 тысяч таких школ по всему миру. Исключая Россию.
Выводы:
Навыки устного счета необходимы каждому человеку.
Приёмы «быстрого» устного счёта применяют 12% учащихся 5 – 9 классов нашей школы (по данным нашего опроса)
Мы овладели приёмами сложения и вычитания многозначных чисел на счётах, при этом автоматически улучшили навыки устных вычислений.
Рекомендуем использовать русские счёты для формирования навыков устных вычислений.
Преимущества счётов для формирования вычислительных навыков (против счётных палочек):
Дешевизна,
Надёжность: уронишь не сломаются,
В отличие от счётных палочек, не теряются косточки, т.к. нанизаны на спицы
Простота.
Безопасность в виде отсутствия электромагнитных излучений и поражений током.
Визуализация приёмов вычислений.
Развитие памяти.
Введение в математику. Определение счёта, единицы и числа
Математика – это совокупность наук, изучающих величины, количественные отношения, а также пространственные формы. Изучение математики начинается с раздела арифметики.
Арифметика – это наука о числах. В арифметике изучаются простейшие свойства чисел и различные способы вычислительных операций над ними.
Основополагающими понятиями в арифметике являются счёт, единица и число.
Определение счёта, единицы и числа
Чтобы узнать количество объектов (например, карандашей) или действий (например, приседаний), их нужно сосчитать. Счёт – это определение количества чего-либо.
Каждый отдельный объект или каждое отдельное действие при счёте называется единицей. Результат счёта, то есть количество посчитанных единиц, выражается числом. Число – это определённое (посчитанное) количество единиц.
Число позволяет дать ответ на вопрос сколько?
(например: сколько яблок на тарелке?).
Числа можно выражать двумя способами: устно и письменно, с помощью специальных символов. Способ выражать числа устно называется устной нумерацией. Способ выражать числа письменными знаками (символами) называется письменной нумерацией.
Множества
В математике любую группу объектов можно назвать множеством. Каждый объект из группы называется элементом множества.

На картинке изображено два множества: множество цифр и множество геометрических фигур. Цифра 5 – элемент множества цифр, а квадрат — элемент множества геометрических фигур.
Множество – это группа объектов, объединённых по какому-то общему признаку.
Если множества состоят из одних и тех же объектов, то они равны, а если из разных объектов, то не равны:

