Как называется методика быстрого счета: Как научиться быстро считать в уме любые числа: техники устного счета — Школа №12 — Научно-образовательный центр школы №12 г. Челябинска

Содержание

Методика быстрого счета без калькулятора

Цифры окружают нас с детства. Еще до школы или в первом классе человек учится складывать и вычитать, решать простые примеры и задачи. Позже он осваивает таблицу умножения, переходя к более сложной части математических упражнений. Большинство людей может производить в уме только простые вычисления. А вот умножение и деление больших значений приходится выполнять на бумаге или с помощью калькулятора. Но можно ли как-то научиться хорошо считать без использования подручных средств?

Быстрый счет без калькулятора

Жизнь любого современного человека неотрывно связана с числами. Без умения считать невозможно выполнять самые простые повседневные задачи. Конечно, сегодня у людей появились умные помощники – калькуляторы, смартфоны, компьютеры, но даже они могут иногда подвести – сломаться или не вовремя разрядиться. Да и не всегда можно полагаться на гаджеты, ведь на экзаменах в школе или в ВУЗе они не помогут. Именно поэтому многие люди стремятся научиться хорошо считать без помощи подручных средств. Особенно это актуально для школьников, ведь если с детства освоить техники быстрого устного счета, то и учеба в школе, и различные задачи во взрослой жизни будут даваться легче.

Есть еще одна серьезная причина для того, чтобы начать тренироваться хорошо считать в уме. Устный счет развивает человеческий мозг и способствует росту уровня интеллекта. Поэтому даже те студенты, которые обучаются на гуманитарных специальностях, все равно изучают такие точные науки, как высшая математика и математический анализ. Упражнения, направленные на устный счет больших чисел, являются отличной зарядкой для ума. Так развитие интеллекта и удобство в быту – это две самые главные причины научиться хорошо считать без калькулятора.

Человечество еще с древности стремилось найти такие способы быстрого счета. И речь не только о простых вычислениях, таких как сложение и вычитание, но и о более сложных – об умножении и делении. Пусть это и занимает много времени, но складывать и вычитать большие значения все же можно без предварительной подготовки, а вот такие действия, как умножение двузначных чисел, недоступны большинству людей.

Но, благодаря труду математиков со всего земного шара, сегодня появились некоторые математические хитрости, позволяющие считать в уме не только однозначные, но и двузначные числа. Чтобы понять принцип их работы, лучше рассмотреть каждый из этих приемов отдельно.

Как научить ребенка считать в уме

Ментальная арифметика – это далеко не новая система быстрого счета, ведь она зародилась еще в древности, около пяти тысяч лет назад. С тех пор данная методика не претерпела серьезных изменений и дошла до нас в практически первозданном виде. В ее основе лежат вычисления на абакусе – специальных счётах. Сначала человек учится решать простейшие примеры на них, а затем постепенно переходит к более сложному этапу обучения – учится представлять абакус в уме и производить вычисления на нем в своем воображении.

Лучше всего ментальная арифметика подходит именно детям. Нет, взрослые также могут ее освоить, но для этого им придется абстрагироваться от привычных методов операций с числами, а ребенок справляется с этим намного легче. Для него ментальная арифметика является не только помощником на уроках математики, но и способом развить свои интеллектуальные способности до очень высокого уровня.

Весь секрет этой методики в том, что она подразумевает разностороннее развитие человека. За логику и анализ отвечает правое полушарие мозга, именно оно задействуется на обычных уроках математики, когда мы решаем примеры или задачи. Правое полушарие, отвечающее за креативное мышление и фантазию, в этом случае к работе почти не подключается, а значит и не развивается должным образом. А ведь все области человеческого интеллекта необходимо тренировать.

Так как ментальная арифметика задействует и аналитическое мышление, и воображение, она является даже не столько способом быстро решать математические задачи, сколько средством для всестороннего развития. Другие методики чаще всего направлены на тренировку какой-то одной способности, а данная техника работает комплексно. Именно это выделяет ее среди прочих и делает одной из самых популярных систем развития интеллекта ребенка.

Обучение ментальной арифметике занимает достаточно много времени, но те преимущества, которые она дает, оправдывают затраченные усилия. Когда речь идет об обучении ребенка по данной методике, важно подобрать правильную программу тренировок. Ключевым фактором успеха является соблюдение плана занятий и контроль их регулярности. Несмотря на то, что в открытых источниках в интернете можно найти много информации по этому запросу, не всегда удается самостоятельно освоить ментальную арифметику. Поэтому большинство родителей предпочитают обучать ребенка этой технике в детских центрах дополнительного образования.

Как выбрать эффективную методику

Сегодня многие учебные заведения предлагают пройти курсы ментальной арифметики. Но детское образование – это очень сложный и многогранный процесс, поэтому родители должны походить к нему внимательно, и выбирать такие занятия, которые точно принесут пользу.

Выбирая школу ментальной арифметики, обращайте внимание на то, чтобы обучение велось по проверенной методике и учитывало возрастные особенности каждого ребенка. Нельзя, чтобы в одной группе обучались дети из начальной школы и старшеклассники, ведь в каждом возрасте своя скорость освоения, запоминания и закрепления материала.

К тому же, маленьким детям лучше всего преподавать любой предмет в игровой форме. Так они не будут уставать учиться и смогут сохранять концентрацию в течение всего урока. Внедрение игры в образовательный процесс способствует повышению интереса ребенка к математике.

Очень важно, чтобы тренер успевал уделить внимание каждому ученику в процессе занятия, но это возможно только в небольших группах. Поэтому стоит отдавать предпочтение тем детским центрам, где педагог обучает не более десяти детей единовременно. Только тогда удастся заниматься с максимальной продуктивностью.

Если учебный план организован правильно, то ребенку удастся приобрести полезные навыки, благодаря которым математика станет для него интересным и любимым предметом. Все это положительно скажется на успеваемости в школе, ведь, когда учеба дается легко, заниматься намного веселее.

Все это делает обучение ментальной арифметике самым продуктивным способом освоения быстрого устного счета.Ребенку больше не придется прибегать к различным математическим хитростям, чтобы легко справляться с задачами и примерами. Ученик приобретает навыки, которые сохраняются на всю жизнь, а значит они пригодятся ему не только в учебе, но и в карьерной деятельности. Все это делает обучение данной технике отличным вкладом в будущее своего ребенка.

Ментальная арифметика: что это такое за методика

СОДЕРЖАНИЕ

В современном мире дети с легкостью справляются с гаджетами, компьютерными программами, но при этом не могут похвастаться хорошей успеваемостью в школе. Психологи отмечают, что у некоторых детей присутствует недостаток концентрации, внимания и мотивации к обучению. Из-за чего родителям сложно заинтересовать ребенка в изучении какого-либо предмета и распознать его склонность к каким-либо наукам. Как ни удивительно, но базовую проблему внимания и любознательности решают занятия по ментальной арифметике, которая развивает умственные и творческие способности ребенка, заставляет запоминать, учить, разбираться. Польза от занятий ментальной арифметикой уже была доказана многими зарубежными исследованиями. Теперь с этим предметом знакомятся и дети в России.

Что такое ментальная арифметика

Ментальная арифметика — это методика гармоничного развития интеллекта, при которой используется азиатская технология вычислений при помощи разновидности счетов — абакус (соробан). Программу занятий составляют механические упражнения пальцами на счетах, счет в уме и упражнения на концентрацию, внимание и логику. Помогает значительно увеличить скорость мышления и способность к творческим дисциплинам. Подходит детям и взрослым.

Результатом занятий является способность быстро вычислять в уме многозначные цифры без использования калькулятора. Часто занятия по ментальной арифметике называет ментальной математикой.

Когда лучше изучать

Наибольший результат дает изучение ментальной арифметикой в возрасте от 4 до 16 лет. Это обусловлено биологическими возможностями организма воспринимать новую информацию. Но изучение ментальной арифметике в старшем возрасте дает еще больший эффект! За счет упражнений восстанавливается моторика рук и повышается нейропластичность мозга.

Как происходит обучение

Программа занятий включает в себя несколько этапов:

Работа со счетами абакус. При тренировочных упражнениях на счетах развивается мелкая моторика, стимулируется развитие межполушарных связей. Благодаря техническим упражнениям на абакусе увеличивается скорость мышления, усидчивость, развивается концентрация. На первом этапе обучения ребенок учится правильной технике выполнения счета на абакусе и осваивает все операции первоначально на абакусе.
Вычисления в уме или ментальный счет. Это результат работы системы упражнений на абакусе, когда ребенок уже готов к образному вычислению. Основой ментального счета считается визуализация ментальной карты в уме и операции бусинами без представления цифр.

После правильного выполнения упражнений видимым результатом станет поразительно быстрое вычисление примеров. Хотя развитие интеллекта благодаря занятиям ментальной арифметикой происходит гораздо глубже и эффективнее. Нейронные связи, сформированные благодаря упражнениям на занятиях, остаются с ребенком на всю жизнь. А это значит, что ребенок научился быстро концентрироваться, визуализировать информацию и быстро оперировать данными.

См. также Ментальная арифметика для детей онлайн

Польза ментальной математики для детей

Развивает творческие способности
В школе предметы преимущественно заточены на развитие левого полушария мозга и, практически исключают развитие правого полушария, которое в общем отвечает за реализацию творческого потенциала. Благодаря занятиям ментальной арифметикой мозг ребенка включает программу гармоничного развития — работают аналитические способности левого полушария и визуально-пространственные способности правого, что способствует более быстрому развитию всего интеллекта.
Улучшает понимание математики
Ментальная арифметика помогает подружить ребенка с цифрами. Вместо того, чтобы зубрить скучные правила, ребенок начинает играть. Настольные игры, логические упражнения и элементы квеста на занятиях делают обучение полноценным. Благодаря разработанным возрастным программам обучения в Абакус центре дети с радостью приходят на занятия.
Убирает рассеянность и невнимательность
Ментальный счет требует высокой степени концентрации. Сначала дети развивают усидчивость и концентрацию на счетах абакус, при помощи флеш-карт, а затем при выполнении операций в уме. Освоив технику один раз, дети используют ее не только при решении математических заданий, но и в других школьных предметах.
Развивает визуально-пространственного мышление
Когда ребенок вычисляет ментально, ему приходится держать в голове не только определенные образы, а также правила вычислений. За счет упрощенного вида — образа абакуса — эти вычисления не являются громоздкими и тяжелыми, а наоборот, помогают ребенку играть воображением и, таким образом развивать визуально-пространственное мышление, например, такое необходимое для решения геометрических задач.
Кроме того, вычисления в уме не становятся для ребенка проблемой. Особенно это если ребенок не справлялся со школьными математическими диктантами и испытывал постоянный стресс.
Тренирует память (в том числе и зрительную)
В процессе обучения ребенок постоянно работает с образами, запоминает много картинок и действий и, при чем это делает в совершенно непринужденной обстановке. Когда родители жалуются, что у его ребенка «в одно ухо влетело, в другое вылетело» — это проблема запоминаемости (зрительной и краткосрочной, оперативной памяти). Эту проблема перестает существовать у тех, кто постоянно тренируется на занятиях.
Умение быстро ориентироваться
Выполняя упражнения, ребенок учится быстро ориентироваться и выполнять несколько действий одновременно, сохраняя при этом концентрацию и внимание. Такая согласованность действий поможет на контрольных и экзаменах, где часто ребенок теряется из-за стрессового состояния.
Развивает нематематические навыки
Хотя предмет ментальной арифметики и основные упражнения в своей основе содержат арифметику, тем не менее, занятия развивают очень полезные социальные навыки — умение достигать результата и побеждать, доводить начатое до конца, общению среди сверстников, выдавать готовый результат и многое другое. Дети становятся увереннее в своих достижениях, снимают психологическое напряжение.
С помощью этой методики ребенок сможет одинаково успешно считать, рисовать, изучать иностранные языки и осваивать точные науки. Родители откроют в своем ребенке не только способности «технаря», но и «гуманитария» и наоборот — те, кто ранее сомневался в своих математических способностях, смогут показать лучшие результаты. Более того, ребенок легче сможет переключаться между предметами в течение всего дня и не испытывать усталости.
Доказывает, что учеба может быть веселой
Сама методика построена таким образом, что делает весь процесс обучения интересным, в отличие от стандартного процесса получения знаний, который вызывает у детей скуку и раздражение. Кроме необычных заданий существуют множество занимательных упражнений, которые ребенок выполняет с радостью. Самое главное, что вся программа построена в интересах ребенка, сохраняя при этом педагогические принципы развития личности. Дети не просто становятся увереннее в своих знаниях, они приобретают привычку быть успешными, что позволит в будущем добиться высоких результатов!

Плюсы и минусы ментальной арифметики для детей

А теперь подытожим всё, о чем было рассказано и выделим основные достоинства и нюансы методики.

Плюсы ментальной арифметики

Развитие памяти, внимания, концентрации.
Потенциал ко многим наукам и гибкость мышления.
Раскрытие талантов ребенка.
Легкое обучение счету, действиям с числами.
Тренировка образного мышления.
Усидчивость и собранность.
Интерес к учебе и новым знаниям.
Открытие творческих способностей.
Уверенность в себе.
Развитие способности не пасовать перед сложными задачами, а разбираться в них.
Желание учиться.

Минусы методики

«Не так, как в школе».
Да, методика ментальной арифметики имеет гораздо более широкую направленность и не совпадает со российской школьной программой по математике. Но данная методика подтверждена исследованиями психологов и преподавателей детей, где программа реализуется в начальных классах — Китае, Сингапуре, Японии и др.
Главное дать возможность ребенку раскрыть свой потенциал, привить любовь к процессу обучения, усидчивость, разработать мышление, укрепить его память и убрать страх перед любыми уроками и познанием нового!
Поспешность и ошибки.
Некоторые дети и их родители слишком спешат с выполнением заданий и допускают ошибки. Этого можно избежать, если процесс обучения будет под руководством опытного педагога. Кроме того, ошибок становится гораздо меньше с повышением уровня знаний ребенка.
Перегрузка и обратный эффект.
Когда детям интересно, они хотят заниматься этим постоянно. Но родители должны понимать, что ментальная математика — это все-таки наука и кропотливое дело, которое должно прерываться отдыхом, досугом, прогулками ребенка. Не надо стараться выполнить «пятилетку за 3 года», не допускайте перегрузок и усталости иначе грозит обратный эффект — абсолютное неприятие предмета. Для формирования ментального счета требуется время, будете терпеливы.

Занятия ментальной арифметикой — это уникальная возможность подарить ребенку будущее, к которому он будет подготовлен.

Эффективные способы быстрого счета в уме

На чтение 11 мин. Просмотров 336 Опубликовано 27.09.2018

Многие спрашивают, как научиться быстро считать в уме, чтобы это выглядело незаметно и неглупо. Ведь современные технологии позволяют меньше пользоваться своей памятью и умственными способностями. Но иногда нет под рукой данных технологий и порой легче и быстрее посчитать что-то в уме. Многие люди начали считать на калькуляторе или телефоне даже элементарные вещи, что также не очень хорошо. Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него. Возможность обходиться без специальных девайсов и в нужный момент оперативно решить поставленную арифметическую задачу – это не единственное применение данного навыка. Помимо утилитарного назначения, приемы устного счета позволят научиться организовывать себя в различных жизненных ситуациях. Кроме того, умение считать в уме, несомненно, положительно скажется на имидже ваших интеллектуальных способностей и выделит вас среди окружающих «гуманитариев».

Способы быстрого счета

Существует определенный набор простейших арифметических правил и закономерностей, которые не только нужно знать для устного счета, но и постоянно держать в голове, чтобы в нужный момент оперативно применить самый эффективный алгоритм. Для этого необходимо довести их использование до автоматизма, закрепить в машинальной памяти, чтобы от решения самых простых примеров успешно перейти к более сложным арифметическим действиям. Вот основные алгоритмы, которые нужно знать, помнить и применять мгновенно, автоматически:

Вычитание 7, 8, 9

Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам нужно привыкнуть к этому новому способу.

Умножение на 9

Быстро умножить любое число на 9 можно при помощи пальцев рук.

Деление и умножение на 4 и 8

Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно.

Например, 46*4=46*2*2 =92*2= 184.

Умножение на 5

Умножать на 5 очень просто. Умножение на 5, и деление на 2 – это практически одно и то же. Так 88*5=440, а 88/2=44, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10.

Умножение на 25

Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120*25 = 120/4*100=30*100=3000.

Умножение на однозначные числа

Чтобы быстро считать в уме, полезно уметь умножать двузначные и трехзначные числа на однозначные. Для этого нужно умножать двух- или трехзначное число поразрядно.

Например, умножим 83*7.

Для этого сначала умножим 8 на 7 (и допишем ноль, так как 8 — разряд десятков), и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7 +3*7= 560+21=581.

Возьмем более сложный пример: 236*3.

Итак, умножаем сложное число на 3 по разрядно: 200*3+30*3+6*3=600+90+18=708.

Определение диапазонов

Чтобы не запутаться в алгоритмах и по ошибке не выдать совсем неверный ответ, важно уметь строить примерный диапазон ответов. Так умножение однозначных чисел друг на друга может дать результат не более 90 (9*9=81), двузначных — не более 10 000 (99*99=9801), трехзначных не более — 1 000 000 (999*999=998001).

Раскладка на десятки и единицы

Способ заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

Например:

63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 +3*5=4800+300+240+15=5355

Проще такие примеры решаются в 3 действия:

1. Сначала умножаются десятки друг на друга.
2. Потом складываются 2 произведения единиц на десятки.
3. Затем прибавляется произведение единиц.

Схематично это можно описать так:

— Первое действие: 60*80 = 4800 — запоминаем
— Второе действие: 60*5+3*80 = 540 – запоминаем
— Третье действие: (4800+540)+3*5= 5355 – ответ

Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.

Мысленная визуализация умножения в столбик

56*67 – посчитаем в столбик. Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа.

Но его можно упростить:
Первое действие: 56*7 = 350+42=392
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752

Частные методики умножения двузначных чисел до 30

Преимуществом трех способов умножения двузначных для устного счета состоит в том, что они универсальны для любых чисел и при хорошем навыке устного счета, они могут позволить вам достаточно быстро прийти к правильному ответу. Однако эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов.

Умножение на 11

Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры.

Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.

Если сумма чисел в центре дает результат больше 10, тогда добавляем единицу к первой цифре, а вместо второй цифры пишем сумму цифр умножаемого числа минус 10.

Например: 29*11 = 2 (2+9) 9 = 2 (11) 9 = 319.
Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа.

Например: 324 * 11=3(3+2)(2+4)4=3564

Квадрат суммы, квадрат разности

Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:

23²= (20+3)2 = 202 + 2*3*20 + 32 = 400+120+9 = 529

69² = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761

Возведение в квадрат чисел, заканчивающихся на 5.Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.

25² = (2*(2+1)) 25 = 625

85² = (8*(8+1)) 25 = 7 225

Это верно и для более сложных примеров:

155² = (15*(15+1)) 25 = (15*16)25 = 24 025

Методика умножения чисел до 20 очень проста:

16*18 = (16+8)*10+6*8 = 288

Доказать правильность этого метода просто: 16*18 = (10+6)*(10+8) = 10*10+10*6+10*8+6*8 = 10*(10+6+8) +6*8. Последнее выражение и является демонстрацией описанного выше метода. По сути, этот метод является частным способом использования опорных чисел . В данном случае опорным числом является 10. В последнем выражении доказательства видно, что именно на 10 мы умножаем скобку. Но в качестве опорного числа можно использовать и любые другие числа, из которых наиболее удобными являются 20, 25, 50, 100…

Опорное число

Посмотрите на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8.

Для того, чтобы узнать их произведение, нужно совершить следующие операции:

15*18

1. К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.
2. Затем 23 умножаем на опорное число, то есть на 10. Ответ: 230
3. К 230 прибавляем произведение 5*8. Ответ: 270.

Опорное число при умножении чисел до 100.Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа
Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100.
Методика использования опорного числа зависит от того, являются ли множители больше или меньше опорного числа. Тут возможны три случая. Покажем, все 3 методики на примерах.
Оба числа меньше опорного (под опорным). Допустим, мы хотим умножить 48 на 47.
Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа.
Чтобы умножить 48 на 47, используя опорное число 50, нужно:

47*48

1. Из 47 вычесть столько, сколько не хватает 48 до 50, то есть 2. Получается 45 (или
из 48 вычесть 3 – это всегда одно и то же)
2. Дальше 45 умножаем на 50 = 2250
3. Затем прибавляем 2*3 к этому результату – 2 256

50 (опорное число)

47 48

3(50-47) 2(50-48)

(47-2)*50+2*3=2250+6=2256

Если числа меньше опорного, то из первого множителя вычитаем разность между опорным числом и вторым множителем. Если числа больше опорного, то к первому множителю прибавляем разность опорного числа и второго множителя .

50(опорное число)

51 63

1 13

(51+13)*50+(13*1)=3200+13=3213

Одно число под опорным, а другое над.Третий случай использования опорного числа – когда одно число больше опорного, а другое меньше. Такие примеры решаются не сложнее, чем предыдущие. Меньший множитель увеличиваем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей. Или больший множитель уменьшаем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей.

50(опорное число)

45 52

5(50-45) 2(52-50)

(52-5)*50-5*2=47*50-10=2340 или (45+2)*50-5*2=47*50-10=2340

При умножении двузначных чисел из разных десятков в качестве опорного числа удобнее
брать круглое число , которое больше большего множителя.

27*89

90(опорное число)

27 89

63 (90-27) 1 (90-89)

(89-63)*90+63*1=2340+63=2403

Таким образом, с помощью использования одного опорного числа можно умножать большую комбинацию двузначных чисел. Описанные выше методики можно разделить на универсальные (подходящие для любых чисел) и частные (удобные для конкретных случаев).

В крайнем случае, можно воспользоваться «крестьянским» счетом. Чтобы умножить одно число на другое, допустим 21*75, нам нужно записать числа в две колонки. Первое число левой колонки 21, первое число правого столбика 75. Затем числа стоящие в левой колонке делить на 2 и отбрасывать остаток, пока не получим единицу, а числа в правой колонке умножаем на 2. Все строчки, имеющие четные числа в левой колонке вычеркиваем, а оставшиеся числа в правой колонке складываем, у нас получается точный результат.

21*75

21 75

10 150

5 300

2 600

1 1200

Чтобы научиться быстро считать в уме, нужна практика, нет волшебных методик, чтобы с первого раза начать быстро считать в голове, необходимо постоянно тренировать свой мозг и заставлять его быстро работать и считать.

Заключение

Как и все способы вычислений, данные методы быстрого счета имеют свои достоинства и недостатки:

ПЛЮСЫ:

1.С помощью различных методов быстрых вычислений даже самый малообразованный человек может считать.
2. Способы быстрого счета могут помочь избавиться от сложного действия, путем замены его на несколько более простых.
3.Способы быстрого счета полезны в ситуациях, когда нельзя воспользоваться умножением в столбик.
4.Способы быстрого счета позволяют сократить время вычислений.
5.Устный счет развивает умственную деятельность, что помогает быстрее ориентироваться в сложных жизненных ситуациях.
6. Техника устного счета делает процесс вычислений более увлекательным и интересным.

МИНУСЫ:

1.Зачастую, решать пример, пользуясь способами быстрого счета, оказывается дольше, чем просто перемножать в столбик, так как приходится выполнять большее количество действий, каждое из которых проще первоначального.
2.Бывают ситуации, когда человек от волнения или еще чего-то забывает способы быстрого счета или вовсе — путается в них; в таких случаях ответ получается неправильным, а способы являются фактически бесполезными.
3.Не для всех случаев разработаны способы быстрого счета .
4.Вычисляя с использованием техники быстрого счета, нужно держать множество ответов в голове, в чем можно запутаться и прийти к ошибочному результату.

Несомненно, практика играет важнейшую роль в развитии любых способностей. Но навык устного счета не опирается на один лишь опыт. Это доказывают люди, которые способны считать в уме сложные примеры. Например, такие люди могут умножать и делить трехзначные числа, совершать арифметические операции, которые не каждый человек и в столбик сможет посчитать. Что же необходимо знать и уметь обычному человеку, чтобы овладеть такой феноменальной способностью? На сегодняшний день существуют различные методики, помогающие научиться быстро считать в уме.

Изучив многие подходы к обучению навыку считать устно, можно выделить 3 основных составляющих данного навыка:

1. Способности. Способность концентрировать внимание и умение удерживать в краткосрочной памяти несколько вещей одновременно. Предрасположенность к математике и логическому мышлению.

2. Алгоритмы. Знание специальных алгоритмов и умение оперативно подобрать нужный, максимально эффективный алгоритм в каждой конкретной ситуации.

3. Тренировка и опыт, значение которых для любого навыка никто не отменял. Постоянные тренировки и постепенное усложнение решаемых задач и упражнения позволят вам улучшить скорость и качество устного счета. Нужно отметить, что третий фактор имеет ключевое значение. Не обладая необходимым опытом, вы не сможете удивить окружающих быстрым счетом, даже если вы знаете самый удобный алгоритм. Однако не стоит недооценивать важность первых двух составляющих, поскольку имея в своем арсенале способности и набор нужных алгоритмов, вы сможете удивить даже самого опытного «счетовода», при условии, что вы тренировались одинаковое время.

Эффективный счёт в уме или разминка для мозга / Хабр Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:

Используем круглые числа

Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:

Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:

31 x 29 = (30 + 1) x (30 - 1) = 30 x 30 - 1 x 1 = 900 - 1 = 899.

Упростим умножение делением

При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):

68 x 50 = (68 x 100) : 2 = 6800 : 2 = 3400;
3400 : 50 = (3400 x 2) : 100 = 6800 : 100 = 68.

Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,

600 : 25  = (600 : 100) x 4 = 6 x 4 = 24;
24 x 25 = (24 x 100) : 4 = 2400 : 4 = 600.

Теперь не кажется невозможным умножить в уме 625 на 53:

625 x 53 = 625 x 50 + 625 x 3 = (625 x 100) : 2 + 600 x 3 + 25 x 3 = (625 x 100) : 2 + 1800 + (20 + 5) x 3 = 
= (60000 + 2500) : 2 + 1800 + 60 + 15 = 30000 + 1250 + 1800 + 50 + 25 = 33000 + 50 + 50 + 25 = 33125.

Возведение в квадрат двузначного числа

Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:

Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,

37^2 = 12 x 100 + 13^2 = 1200 + 169 = 1369; 
84^2 = 59 x 100 + 34^2 = 5900 + 9 x 100 + 16^2 = 6800 + 256 = 7056;

В общем случае (M — двузначное число):

Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:

195^2 = (100 + 95)^2 =  10000 + 2 x 100 x 95 + 95^2 = 10000 + 9500 x 2 + 70 x 100 + 45^2 = 10000 + (90+5) x 2 x 100 + 
+ 7000 + 20 x 100 + 5^2 = 17000 + 19000 + 2000 + 25 = 38025.

Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.

Умножение двузначных чисел

Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:

M = 10m + n, K = 10a + 10 - n.

Составив их произведение, получим:

Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:

13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 = 800 + 201 = 1001.

У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,

48 x 42 = 2016.

99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,

99 x 91 = 9009.

Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:

95 x 95 = 9025.

Тогда предыдущий пример можно вычислить немного проще:

195^2 = (100 + 95)^2 =  10000 + 2 x 100 x 95 + 95^2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 = 
= 10000 + 19000 + 1000 +  8000  + 25 = 38025.

Вместо заключения

Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.

Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».

Как считать на древних счетах: тренируем мозги

Счёты это вещь, которую уже мало кто помнит. Теперь мир заполонили калькуляторы, ноутбуки и мобильные телефоны. Однако такой давно забытый предмет как счёты очень удобны и нужны людям, о чем сейчас мало кто знает.

История древних счёт

Давным-давно, около 5000 лет назад, в Месопотамии и Древней Греции появилась счетная доска для арифметических вычислении. Она состояла из:

Рамки
Поперечной перекладины (планки)
Спиц, проходящих сквозь перекладину
Косточек, нанизанных на спицы

На каждой спице было нанизано по пять косточек. Одна косточка находилась над перекладиной(планкой), а четыре под ней.

Такие счеты назывались Абак. Со временем они были усовершенствованы в Китае и Японии и стали назваться Суаньпань и Соробан. Спустя какое-то время Абак стали называть Абакусом. Вместе с Ментальной арифметикой, для которой Абакус является основным инструментом, Абакус пришел в Россию.

Учимся считать на счётах

Ментальная арифметика это уникальный курс для развития умственных способностей и творческого потенциала за счёт вычисления на абакусе. Во время обучения у детей гармонично развиваются оба полушария головного мозга, благодаря чему все школьные предметы даются ребёнку с лёгкостью. Она учит ребенка, как считать на счетах.

Научится считать на счётах абакус не очень сложно. Главное ; это тренироваться каждый день, выполнять домашнее задание и верить в себя. Несмотря на доказанные результаты, некоторые родители сомневаются, стоит ли отдавать ребёнка на ментальную арифметику. Ведь у него большая нагрузка в школе, репетиторы, плюс он ходит на легкую атлетику. Будет ли малыш всё успевать? Прелесть этой методики в том, что она поможет ребёнку быстрее делать домашнее задание, правильно распределять время, сформировать уверенность в себе.

Смысл данной программы ; тренировка головного мозга для максимальной скорости восприятия и обработки информации. На занятиях по ментальной арифметике дети сначала учатся, как считать на счётах абакус, механически перебирая косточки. Потом ученики представляют счёты в уме и пытаются считать на ментальных счётах.

Учим ребёнка считать на счётах абакус

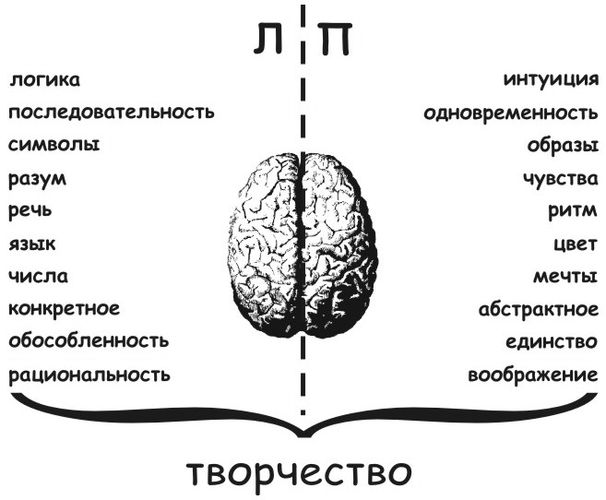
В школе у ребят развивают в большинстве своём левое полушарие мозга, которое отвечает за логику, речь, мелкую моторику и аналитические операции. Занимаясь же ментальной арифметикой, у ребёнка вместе с левым полушарием одновременно развивается и правое. Последнее ответственно за воображение, образное мышление, фантазию.

Оптимальный возраст для обучения от 5 лет. Существуют курсы и для подростков 13-16 лет. Но лучше начать ходить на занятия, когда ребёнок находится ещё в дошкольном возрасте. Потому что тогда у него мозг очень пластичный и занятия проходят более успешно.

На занятиях по ментальной арифметике мы учим ребенка считать на счётах. Благодаря этой методике у ребёнка развивается воображение. От этого появляется любовь к чтению. Научившись быстро считать, малыш завоюет авторитет в детском саду и школе, что поднимет его в глазах одноклассников и сформирует лидерские качества.

Преимущества ментальной арифметики для детей

Формирование мелкой моторики рук за счёт перебирания косточек на абакусе.
Гармоничное развитие левого и правого полушарий головного мозга за счёт работы на абакусе обоих рук.
Тренировка зрительной памяти, потому что ребенок проводит в уме сложные арифметические операции.
Получение такого навыка как быстрый устный счёт. Ребенок сможет решать примеры с многозначными числами быстрее калькулятора.
Подход к решению любых задач двумя способами: аналитическим и творческим.
Развитие сосредоточенности, концентрации внимания, образного мышления, воображения, наблюдательности.
Умение быстро принимать решения и повышение уровня ответственности.

Положительное влияние ментальной арифметики

С помощью абакуса малыш через год-два сможет умножить и делить многозначные числа в уме. Некоторые родители волнуются, а не будет ли мозг их ребенка излишне загружен? Будет ли в нём место для другой полезной информации?

Бояться не стоит. Ментальная арифметика входит в официальную школьную программу почти во всех учебных заведениях Азии. И как отмечает история, у детей складывается только положительная динамика:

Усиление зрительной и слуховой памяти;
Увеличение концентрации внимания;
Активизация смекалки и интуиции;
Возникновение самостоятельности и уверенности;
Формирование нестандартного мышления;
Получение хорошего высшего образования и престижной работы;
Изучение иностранных языков;
Развитие творческих способностей.

Глядя на этот список, становится не совсем ясно, как математика влияет на всё выше перечисленное. Но в этом и есть особенность этой уникальной методики. Вычисления на абакусе помогают сформировать связь между двумя полушариями мозга.

Правое отвечает за:

интуицию
образное мышление
воображение
способность к творчеству
понимание подтекста
ориентацию в пространстве
музыкальный слух
обработку материала из нескольких источников сразу

Левое отвечает за:

речь
чтение
письмо
память
логику
рациональное мышление
числа и символы
последовательность событий

А совместная деятельность обоих полушария и даёт такой впечатляющий эффект.

Что такое счетчик времени с одним фотоном?

О нас
Новости
События
Наш блог
Карьера

Английский (Великобритания)
- английский (США)
- Français
- Deutsch
- английский (IN)
- 한국어

ПРОДУКТЫ
ТЕХНОЛОГИИ
- Стационарная флуоресценция
- Временная флуоресценция
- Время жизни фосфоресценции
- Рамановская спектроскопия
- Ультра-видимая спектроскопия
- Ресурсы
- Ресурсы
- Ресурсы
- Ресурсы
- Ресурсы
- Ресурсы
- Ресурсы
- Ресурсы
- Ресурсы Видео / Учебники
ПРИЛОЖЕНИЯ
ПОДДЕРЖКА
КОНТАКТЫ

Поиск:

Флуоресцентный спектрометр

FLS1000 Фотолюминесцентный спектрометр
FS5 Спектрофлуориметр
Lifeespec II Пожизненный спектрометр
Программное обеспечение Mini-tau Lifetime

Программное обеспечение

9000 9000 9000 Программное обеспечение

Программное обеспечение

Программное обеспечение для управления

Программное обеспечение

Программное обеспечение для управления

Программное обеспечение

Программное обеспечение для управления

Рамановский контроль и анализ

Ramacle Software

Управление переходным поглощением и анализ

Программное обеспечение L900
Расширенное программное обеспечение FLASH

Рамановские микроскопы

светодиоды и микроскопы RM5

Пикосекундные импульсные диодные источники
- Импульсные диодные лазеры — VIS / NIR
- Импульсные светодиоды — UV / Vis
CO / CO2 Газовые лазеры
- CO Laser (5.2 — 6,0 мкм)
- CO2-лазеры (9,1 мкм-10,9 мкм)
- MTL-5 Мини-TEA CO2-лазер
Дальний инфракрасный / терагерцовый лазер
- 295 — Однополостный ИК-лазер
- 395 — Twin Cain FIR Laser
- FIRL-100 FIR Лазер (7,5 ТГц — 0,25 ТГц)
Laser Services
- Laser Services

Обновления

Обновления флуоресцентных спектрометров
- Обновления FLS1000
- Обновления FLS1000
- Обновления
- FS5 Модернизация системы
- LifeSpec II Обновление
- Мини-тау Обновления
Transient Поглощение спектрометры Обновление
- LP980 Обновление
- LP920 Обновление
Raman Микроскоп Обновление
- RM5 Обновление

УФ- Vis Спектрофотометр

DS5 Двухлучевой UV-Vis Спектрофотометр

Переходный Поглощение

LP980 пролетных абсорбционный спектрометр

Настройка и Ex Demo

Настроенных оборудование Опция
- Персонализации
Ex-Demo оборудование
- Ex Demo оборудование

Просмотреть все продукты

ПРОДУКТОВ
- Флуоресцентных Спектрометры
  - FLS1000 Фотолюминесцентный спектрометр
  - FS5 Спектрофлуориметр
  - Lifeespec II Lifetime Spectrometer
  - Mini-tau Lifetime Спектрометр
- Программное обеспечение
  - Photoluminescence
  - Программное обеспечение
  - Программное обеспечение
  - Программное обеспечение
  - Программное обеспечение для управления
  - Раман-контроль и анализ
    - Ramacle Software
  - Управление и анализ переходного поглощения
    - L900 Программное обеспечение
    - Advanced FLASH Software
- Rama n Микроскопы
  - Рамановский микроскоп RM5
- Лазеры и светодиоды
  - Пикосекундные импульсные диодные источники
    - Импульсные диодные лазеры — VIS / NIR
    - Импульсные светодиоды — Ультрафиолетовый / видимый излучатели
    - CO 2 CO. (5.2–6,0 мкм)
    - CO2-лазеры (9,1–10,9 мкм)
    - MTL-5 Mini-TEA CO2-лазер
  - Дальний инфракрасный / терагерцовый лазер
    - 295 — Однополостный FIR-лазер
    - 395 — Twin Cain FIR Laser
    - FIRL-100 FIR Laser (7,5 ТГц — 0,25 ТГц)
  - Laser Services
    - Laser Services
- Обновления
  - Флуоресцентные спектрометры Обновления
    - Обновления FLS1000
    - Обновления FLS1000
    - Обновления FLS1000
    - Обновления FLS1000
    - Обновления FLS1000
    - Обновления FLS1000
    - Обновления FLS1000
    - Обновления FLS1000
    - Обновление FLS1000
    - Обновления системы FS5
    - Обновления LifeSpec II

Как быстро заснуть за 10, 60 или 120 секунд

Тратить больше времени на попытки уснуть, а не спать? Ты не один.

Само по себе усилие изо всех сил может вызвать (или продолжить) цикл тревожной, нервной энергии, которая не дает спать нашему уму.

И если ваш разум не может уснуть, вашему телу действительно трудно следовать за ним. Но есть научные приемы, которые вы можете попробовать щелкнуть выключателем и привести свой организм в безопасный режим выключения.

Мы расскажем о некоторых научных приемах, которые помогут вам быстрее заснуть.

Обычно требуется быстрое волшебное заклинание, чтобы заснуть, это быстро и по сигналу, но точно так же, как заклинания, с практикой вы можете в конечном итоге добраться до сладкого 10-секундного места.

Примечание: Для выполнения описанного ниже способа требуется 120 секунд, но, как говорят, последние 10 секунд — это действительно все, что нужно, чтобы наконец отложить сон.

Военный метод

Популярный военный метод, о котором впервые сообщила Шарон Акерман, взят из книги под названием «Расслабься и выиграй: производительность чемпионата.

По словам Акермана, в предполетной школе ВМС США была разработана программа, которая помогает пилотам заснуть за 2 минуты или меньше. Пилотам потребовалось около 6 недель практики, но это сработало — даже после того, как он выпил кофе и слышал выстрелы на заднем плане.

Говорят, что эта практика работает даже для людей, которым нужно спать сидя!

Военный метод

Расслабьте все лицо, включая мышцы рта.
Опустите плечи, чтобы снять напряжение и опустите руки на бок.
Выдохните, расслабив грудь.
Расслабьте ноги, бедра и икры.
Очистите свой разум на 10 секунд, представив себе расслабляющую сцену.
Если это не сработает, попробуйте повторять слова «не думайте» снова и снова в течение 10 секунд.
В течение 10 секунд вы должны заснуть!

Если это не сработает для вас, вам, возможно, придется поработать над основами военного метода: дыханием и расслаблением мышц, которые имеют некоторые научные доказательства того, что они работают.Кроме того, некоторые условия, такие как СДВГ или беспокойство, могут повлиять на эффективность этого метода.

Продолжайте читать, чтобы узнать о методах, на которых основан этот военный метод, и о том, как эффективно их применять.

Эти два метода, которые фокусируются на вашем дыхании или мышцах, помогают вам отвлечься от темы и вернуться в постель.

Если вы новичок, пробующий эти взломы, эти методы могут занять до 2 минут.

4-7-8 метод дыхания

Сочетая силы медитации и визуализации, этот метод дыхания становится более эффективным с практикой.Если у вас есть респираторное заболевание, такое как астма или ХОБЛ, рассмотрите возможность проконсультироваться с врачом перед началом, так как это может ухудшить ваши симптомы.

Чтобы подготовиться, прижмите кончик языка к верхней части рта, за двумя передними зубами. Держи язык там все время и поджав губы, если нужно.

Как сделать один цикл из 4-7-8 дыханий:

Позвольте вашим губам слегка раздвинуться и издайте свистящий звук при выдохе через рот.
Потом закрой губы и тихо вдохни через нос. Считай до 4 в твоей голове.
Затем задержите дыхание на 7 секунд.
После этого выдох (со свистом) в течение 8 секунд.
Не будьте слишком внимательны в конце каждого цикла. Попробуйте практиковать это бездумно.
Завершите этот цикл для четырех полных вдохов. Позвольте вашему телу спать, если вы чувствуете, что расслабление наступает раньше, чем ожидалось.

Прогрессивная мышечная релаксация (PMR)

Прогрессивная мышечная релаксация, также известная как глубокая мышечная релаксация, помогает вам расслабиться.

Идея состоит в том, чтобы напрячь, но не напрягать, мышцы и расслабиться, чтобы снять напряжение. Это движение способствует спокойствию во всем теле. Это трюк, рекомендуемый, чтобы помочь с бессонницей.

Прежде чем начать, попробуйте применить метод 4-7-8, представляя, как напряжение покидает ваше тело при выдохе.

Релаксационный сценарий

Поднимите брови как можно выше на 5 секунд. Это подтянет мышцы лба.
Немедленно расслабьте мышцы и почувствуйте падение напряжения.Подождите 10 секунд.
Широко улыбайтесь, чтобы создать напряжение в ваших щеках. Задержитесь на 5 секунд. Расслабьтесь.
Пауза 10 секунд.
Squint с закрытыми глазами. Держи 5 секунд. Расслабьтесь.
Пауза 10 секунд.
Наклоните голову немного назад, чтобы вы с комфортом смотрели в потолок. Держи 5 секунд. Расслабьтесь, когда ваша шея снова опустится в подушку.
Пауза 10 секунд.
Продолжайте двигаться вниз по остальной части тела, от трицепса до груди, от бедер до ног.
Позвольте себе уснуть, даже если вы не закончите напрягаться и расслаблять остальную часть своего тела.

Делая это, сосредоточьтесь на том, насколько расслабленным и тяжелым чувствует себя ваше тело, когда оно расслаблено и находится в комфортном состоянии.

Если предыдущие методы по-прежнему не работали, возможно, существует скрытая блокировка, которую необходимо устранить. Попробуйте эти методы!

Скажите себе бодрствовать

Также называемое парадоксальным намерением, побудить себя бодрствовать может быть хорошим способом быстрее заснуть.

Для людей — особенно людей с бессонницей — попытки заснуть могут увеличить беспокойство производительности.

Исследования показали, что люди, которые практиковали парадоксальное намерение, засыпали быстрее, чем те, кто этого не делал. Если вы часто испытываете стресс, пытаясь заснуть, этот метод может быть более эффективным, чем традиционные, намеренные дыхательные практики.

Визуализируйте спокойное место

Если счет слишком активирует ваш разум, попробуйте задействовать свое воображение.

Некоторые говорят, что визуализация чего-то может сделать это реальностью, и возможно, что это работает и со сном.

В исследовании, проведенном в 2002 году в Оксфордском университете, исследователи обнаружили, что люди, которые занимались «отвлечением изображений», засыпали быстрее, чем те, кто отвлекался вообще или не получал никаких инструкций.

Отвлечение изображения

Вместо того, чтобы считать овец, попытайтесь представить безмятежную обстановку и все чувства, которые с ней связаны. Например, вы можете представить себе водопад, звуки эха, стремительный поток воды и запах влажного мха.Ключ должен позволить этому образу занимать место в вашем мозгу, чтобы предотвратить повторное засыпание «мыслями, заботами и заботами» перед сном.

Акупрессура для сна

Недостаточно исследований, чтобы уверенно определить, действительно ли точечный массаж работает. Тем не менее, доступное исследование является многообещающим.

Один из методов — нацеливать области, которые вы знаете и чувствуете себя особенно напряженными, например, верхнюю часть переносицы или виски.

Тем не менее, в акупрессуре есть также определенные моменты, которые помогают при бессоннице.Вот три, которые вы можете сделать, не вставая:

1. Духовые врата

Техника

Почувствуйте небольшое полое пространство под вашей ладонью на мизинце.
Осторожно приложите давление круговыми движениями вверх или вниз в течение 2-3 минут.
Слегка надавите левой стороной точки (лицом к ладони) на несколько секунд, а затем удерживайте правую сторону (лицом назад).
Повторите на той же области вашего другого запястья.

2. Внутренние пограничные ворота

Техника

На одной ладони вверх посчитайте три пальца вниз от складки запястья.
Большим пальцем приложите равномерное давление вниз между двумя сухожилиями.
Вы можете делать массаж круговыми движениями вверх-вниз, пока не почувствуете расслабление мышц.

3. Бассейн с ветром

Техника

Сложите пальцы вместе (пальцы касаются друг друга и ладони соприкасаются) и раскройте ладони, чтобы создать форму чашки своими руками.
Положите большие пальцы у основания черепа так, чтобы пальцы касались места соединения шеи и головы.
Приложите глубокое и устойчивое давление, используя круговые или восходящие движения для массажа этой области.
Дышите глубоко и обращайте внимание на то, как ваше тело расслабляется при выдохе.

Если вы опробовали эти методы и все еще не можете заснуть в течение 2 минут или меньше, посмотрите, есть ли другие советы, которые помогут вам сделать вашу спальню более удобной для сна.

Вы пробовали…

скрывая свои часы
принимая теплый душ перед сном
открывая окно, чтобы сохранить прохладу в своей комнате
надевая носки
нежная 15-минутная процедура йоги
помещая телефон далеко со своей кровати
ароматерапия (лаванда, ромашка или шалфей)
прием пищи раньше, чтобы избежать переваривания желудка или стимуляции перед сном

Если вы находите атмосферу в своей комнате вредной для сна, есть инструменты, которые вы можете использовать использовать, чтобы заблокировать шум.Буквально.

Попробуйте инвестировать в плотные шторы, машины с белым шумом (или слушать музыку с помощью таймера автостопа) и беруши, которые вы можете купить онлайн.

С другой стороны, гигиена сна, или чистый сон, реальна и эффективна.

Прежде чем вы по-настоящему освоите военный метод или дыхание 4-7-8, посмотрите, что вы можете оптимизировать для своей спальни для беззвучного сна.

7 популярных соглашений по именованию модульных тестов

В статье представлен скомпилированный список стратегии именования модульных тестов, которой можно следовать, называя их модульные тесты. Статья предназначена для быстрого ознакомления, а не для просмотра нескольких замечательных страниц, таких как следующие. Тем не менее, чтобы узнать больше деталей, пожалуйста, не стесняйтесь получить доступ к одной из этих страниц, перечисленных ниже, и знайте сами.

Ниже приведены 7 популярных соглашений о наименовании модульных тестов, которые были найдены большинством разработчиков и скомпилированы из приведенных выше страниц:

MethodName_StateUnderTest_ExpectedBehavior : Существуют аргументы против этой стратегии, что если имена методов изменяются как часть рефакторинга кода, то также должно меняться имя теста, подобное этому, или становится трудным для понимания на более позднем этапе.Ниже приведены некоторые примеры:
- isAdult_AgeLessThan18_False
- снимать деньги_НеправильноАккаунт_ExceptionThrown
- admitStudent_MissingMandatoryFields_FailToAdmit
MethodName_ExpectedBehavior_StateUnderTest : Немного изменено сверху, но часть разработчиков также рекомендует использовать эту технику именования. Эта методика также имеет недостаток, заключающийся в том, что, если имена методов меняются, становится сложным для понимания на более позднем этапе.Ниже показано, как будут выглядеть тесты в первом примере, если их назвать с использованием этой техники:
- isAdult_False_AgeLessThan18
- снимать деньги_Броски исключений_IfAccountIsInvalid
- admitStudent_FailToAdmit_IfMandatoryFieldsAreMissing
тест [Проверяемая функция] : Эта функция облегчает чтение теста, поскольку проверяемая функция написана как часть названия теста. Хотя есть аргументы, что префикс «test» является избыточным.Однако некоторые разделы разработчика любят использовать эту технику. Ниже показано, как вышеприведенные тесты выглядят так, как если бы они назывались с использованием этой техники:
- testIsNotAnAdultIfAgeLessThan18
- testFailToWithdrawMoneyIfAccountIsInvalid
- testStudentIsNotAdmittedIfMandatoryFieldsAreMissing
Проверяемая функция : Многие полагают, что лучше просто написать проверяемую функцию, потому что в любом случае используются аннотации для определения метода как метода тестирования.Рекомендуется также по той причине, что он выполняет модульные тесты как альтернативную форму документации и избегает запахов кода. Ниже показано, как будут выглядеть тесты в первом примере, если их назвать с использованием этой техники:
- IsNotAnAdultIfAgeLessThan18
- FailToWithdrawMoneyIfAccountIsInvalid
- СтудентНе ДопущенИндикатор Обязательных ПолейAreMissing
Should_ExpectedBehavior_When_StateUnderTest : Этот метод также используется многими, поскольку он облегчает чтение тестов.Ниже показано, как будут выглядеть тесты в первом примере, если их назвать с использованием этой техники:
- Should_ThrowException_When_AgeLessThan18
- Should_FailToWithdrawMoney_ForInvalidAccount
- Should_FailToAdmit_IfMandatoryFieldsAreMissing
When_StateUnderTest_Expect_ExpectedBehavior : Ниже показано, как будут выглядеть тесты в первом примере, если они названы с использованием этой техники:
- When_AgeLessThan18_Expect_isAdultAsFalse
- When_InvalidAccount_Expect_WithdrawMoneyToFail
- When_MandatoryFieldsAreMissing_Expect_StudentAdmissionToFail
Given_Preconditions_When_StateUnderTest_Then_ExpectedBehavior : Этот подход основан на соглашении об именовании, разработанном в рамках разработки на основе поведения (BDD).Идея состоит в том, чтобы разбить тесты на три части, чтобы можно было получить предварительные условия, тестируемое состояние и ожидаемое поведение, которое будет записано в вышеуказанном формате. Ниже показано, как будут выглядеть тесты в первом примере, если их назвать с использованием этой техники:
- Given_UserIsAuthenticated_When_InvalidAccountNumberIsUsedToWithdrawMoney_Then_TransactionsWillFail

Мой личный фаворит — это именные юнит-тесты, основанные на особенностях написания тестируемого класса.Это помогает мне удостовериться, что класс следует за единственной ответственностью. Это также очень помогает в рефакторинге кода.

коллекций. Типы контейнеров. Документация Python 3.8.5.

Исходный код: Lib / collection / __ init__.py

Этот модуль реализует специализированные типы данных контейнеров, предоставляя альтернативы Встроенные контейнеры Python общего назначения, dict , list , набор и кортеж .

`namedtuple ()`	Фабричная функция для создания подклассов кортежей с именованными полями
`deque`	контейнер в виде списка с быстрым добавлением и вставкой на обоих концах
`ChainMap`	dict-подобный класс для создания единого представления нескольких сопоставлений
`Счетчик`	подкласс dict для подсчета хеш-объектов
`OrderedDict`	dict подкласс, который помнит записи заказа были добавлены
`defaultdict`	подкласс dict, который вызывает фабричную функцию для предоставления пропущенных значений
`UserDict`	Оболочка вокруг объектов словаря для упрощенного подкласса dict
`UserList`	Оболочка вокруг объектов списка для упрощения подклассов списка
`UserString`	Оболочка вокруг строковых объектов для упрощения подклассов строк

Класс ChainMap предназначен для быстрой связи нескольких отображений. поэтому их можно рассматривать как единое целое.Это часто намного быстрее, чем создание новый словарь и запуск нескольких вызовов update () .

Класс может использоваться для имитации вложенных областей и полезен при создании шаблонов.

класс коллекций. ChainMap ( * карты )

ChainMap группирует несколько диктовок или других сопоставлений в создать единый обновляемый вид. Если не указаны карты , то один пустой словарь предоставляется таким образом, чтобы в новой цепочке всегда было хотя бы одно отображение.

Соответствующие отображения хранятся в списке. Этот список является общедоступным и может быть доступным или обновленным с использованием атрибута maps . Там нет другого государства.

Поиск выполняет последовательный поиск соответствующих отображений, пока не будет найден ключ. В Контраст, записи, обновления и удаления работают только при первом сопоставлении.

ChainMap включает базовые сопоставления посредством ссылки. Так что если обновляется одно из базовых сопоставлений, эти изменения будут отражены в ChainMap .

Поддерживаются все обычные словарные методы. Кроме того, есть отображает атрибут , способ создания новых подконтекстов и свойство для доступ ко всем, кроме первого сопоставления:

карт: Обновляемый пользователем список сопоставлений. Список упорядочен из первый поиск до последнего поиска. Это единственное сохраненное состояние и может быть изменен, чтобы изменить, какие отображения ищутся. Список должен всегда содержать хотя бы одно отображение.

new_child ( m = нет )

Возвращает новую ChainMap , содержащую новую карту, за которой следует все карты в текущем экземпляре. Если указано м, , она становится новой картой в начале списка отображений; если не указан, используется пустой dict, так что вызов d.new_child () эквивалентно: ChainMap ({}, * d.maps) . Этот метод используется для создание подконтекстов, которые могут быть обновлены без изменения значений в любом родительских отображений.

Изменено в версии 3.4: добавлен необязательный параметр м .

родителей: Свойство, возвращающее новую ChainMap , содержащую все карты в текущий экземпляр кроме первого. Это полезно для пропуска первая карта в поиске. Варианты использования аналогичны нелокальное ключевое слово , используемое во вложенных областях. Варианты использования также параллельны для встроенного супер () функция.Ссылка на d.parents эквивалентна: ChainMap (* d.maps [1:]) .

Обратите внимание, что порядок итераций ChainMap () определяется сканирование отображений с последнего на первое:

 >>> baseline = {'music': 'bach', 'art': 'rembrandt'}
>>> регулировки = {'art': 'van gogh', 'opera': 'carmen'}
>>> список (ChainMap (корректировки, базовый уровень))
['музыка', 'искусство', 'опера']

Это дает тот же порядок, что и серия dict.обновление () звонков начиная с последнего сопоставления:

 >>> комбинированный = baseline.copy ()
>>> комбинированный. обновление (корректировки)
>>> список (комбинированный)
['музыка', 'искусство', 'опера']

См. Также

Класс MultiContext в пакете Enthought CodeTools есть варианты поддержки запись в любое отображение в цепочке.
Класс Django Context для шаблонов это цепочка отображений только для чтения. Это также показывает подталкивание и выталкивание контекстов, аналогичных new_child () метод и родителей собственности.
Рецепт Nested Contexts имеет опции для управления применяются ли записи и другие мутации только к первому отображению или к любое отображение в цепочке.
A

Методика быстрого счета без калькулятора

Быстрый счет без калькулятора

Популярная система быстрого счета

Как научить ребенка считать в уме

Как выбрать эффективную методику

Ментальная арифметика: что это такое за методика

Что такое ментальная арифметика

Когда лучше изучать

Как происходит обучение

Польза ментальной математики для детей

Плюсы и минусы ментальной арифметики для детей

Плюсы ментальной арифметики

Минусы методики

Эффективные способы быстрого счета в уме

Способы быстрого счета

Вычитание 7, 8, 9

Умножение на 9

Деление и умножение на 4 и 8

Умножение на 5

Умножение на 25

Умножение на однозначные числа

Определение диапазонов

Раскладка на десятки и единицы

Мысленная визуализация умножения в столбик

Частные методики умножения двузначных чисел до 30

Умножение на 11

Квадрат суммы, квадрат разности

Опорное число

Заключение

Используем круглые числа

Упростим умножение делением

Возведение в квадрат двузначного числа

Умножение двузначных чисел

Вместо заключения

Как считать на древних счетах: тренируем мозги

История древних счёт

Учимся считать на счётах

Учим ребёнка считать на счётах абакус

Преимущества ментальной арифметики для детей

Положительное влияние ментальной арифметики

Что такое счетчик времени с одним фотоном?

Флуоресцентный спектрометр

Программное обеспечение

Рамановские микроскопы

Обновления

УФ- Vis Спектрофотометр

Переходный Поглощение

Настройка и Ex Demo

Военный метод

Военный метод

4-7-8 метод дыхания

Как сделать один цикл из 4-7-8 дыханий:

Прогрессивная мышечная релаксация (PMR)

Релаксационный сценарий

Скажите себе бодрствовать

Визуализируйте спокойное место

Отвлечение изображения

Акупрессура для сна

Техника

Техника

Техника

Вы пробовали…

Добавить комментарий Отменить ответ