Почему китайские школьники так хорошо знают математику
Оказывается, индивидуальные задания — не всегда лучшее решение
Китайские методы обучения в последние годы стали предметом всеобщего интереса: согласно результатам теста PISA, китайские школьники серьёзно превосходят своих ровесников из других стран в умении читать и считать. Учёные из британского Саутгемптонского университета провели исследование, чтобы узнать, как им это удаётся. О своих выводах они рассказали в колонке для журнала Conversation.
Привет, учитель! Рассылка
Для тех, кто работает в школе и очень любит свою профессию
Интерактивное обучение, в котором участвует сразу весь класс, более эффективно, чем самостоятельная индивидуальная или групповая работа. Чтобы прийти к таким выводам, мы протестировали 563 школьников из английского Саутгемптона и китайского Нанкина — эти два города мы выбрали, поскольку они имеют примерно одинаковый социально-экономический статус. Мы использовали задачи из теста TIMSS, который позволяет сравнить уровень и качество математического школьного образования в разных странах мира. В первом из двух тестов китайские ученики в среднем набрали 83%, в то время как среди английских детей результат был всего 56%. Во втором тесте, который ученики проходили 10 неделями позже, английские ученики улучшили свой результат до 66%, по-прежнему оставаясь далеко позади китайцев, набравших 87%.
Затем с помощью видео мы проанализировали, как проходят уроки в школах обеих стран. Мы обнаружили, что в китайских классах 72% времени занимают интерактивные упражнения для всего класса. В Англии на них отводилось только 24% учебных часов. При этом 47%, то есть почти половину всего времени, английские школьники проводят за индивидуальной или групповой самостоятельной работой. В Китае на выполнение упражнений уходит 28% урока.
Большой процент интерактивного обучения связан с более высокими результатами тестов, в то время как за обилием самостоятельной работы на уроках следуют низкие баллы
Наши результаты подтверждаются десятилетиями проведенных исследований, которые говорят о пользе интерактивных занятий. Когда весь класс активно работает на уроках, а учитель задаёт вопросы и приводит наглядные демонстрации, — это гораздо более эффективно с точки зрения результатов, чем когда ученики заняты самостоятельной работой.
20 советов, как сделать обучение нескучным и эффективным
Важность интерактивных методов обучения особенно заметна в математике из-за иерархичной природы предмета. Когда дети работают сами, они могут застревать на каких-то моментах, им приходится подолгу ждать, прежде чем учитель объяснит эту тему. Это затрудняет процесс обучения и делает его малоэффективным.
В Китае учителя работают со всем классом сразу. К примеру, они просят всех учеников поднять карточки с ответом на вопрос или задачу. Так они могут сразу определить, когда ученики нуждаются в помощи. Непонятные моменты разбирают сразу всем классом, и работа идёт быстро, без задержек и простаивания.
Мы далеко не первые, кто говорит о пользе интерактивных занятий, но во многих школах выполнение индивидуальных заданий остаётся основной формой работы. В Англии половину уроков математики школьники делают упражнения.
Как устроено образование Великобритании
Мы можем только предполагать, какие причины побуждают учителей выбирать проигрышные стратегии. Возможно, учителям начальных школ не хватает опыта преподаваня и уверенности в себе. Если так, совсем неудивительно, что они предпочитают передать бремя обучения в руки учеников, чем нести его самим. А может быть, дело в том, что в европейской традиции принято превозносить индивидуальный подход, поэтому учителя привыкли концентрироваться на каждом ученике в отдельности, а не на классе в целом.
ЧИТАЙТЕ ТАКЖЕ:
Математика в школе: 9 вещей, которые бесят
Что мы знаем об американской школе из мультиков
Как математика спасла мир (и чуть не уничтожила)
Задачка на логику для китайских второклассников поставила в тупик весь мир
Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Однажды на уроке математики ученики 2-х классов в китайских школах получили необычное задание. Решить головоломку оказалось трудно не только детям, но и их учителям. Хотя, чтобы найти правильный ответ, требуются вовсе не особые знания в математике, а лишь способность выходить за рамки привычной действительности.
Редакция AdMe.ru предлагает и вам проверить свое логическое мышление.
Итак, приступим
Некоторые родители, не сумев решить головоломку, пришли к неутешительному выводу, что автор сам является пришельцем с далекой планеты.
В ходе журналистского эксперимента Xinhua задачу предложили 11 школьным преподавателям математики. Из них верный ответ нашли лишь 5. Остальные сошлись во мнении, что задача неразрешима.
Ответ на задачу
Почему?
При кажущейся непохожести у всех инопланетян в первом ряду есть 2 общих признака:
- 3 антеннки с круглыми «помпонами» снаружи
- 1 треугольник внутри
Никто из второго ряда не отвечает этим 2 условиям и не является инопланетянином.
В третьем же ряду такое существо всего одно. Оно и есть инопланетянин.
А вы согласны с таким решением? Если считаете, что инопланетянином может быть кто-то другой, пишите его признаки в комментариях.
Иллюстратор Oleg Guta специально для AdMe.ru
Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
2 китайские задачки для школьников
В интернете активно обсуждают задачку по математике, которую задали школьникам в китайской провинции Сычуань.
Её условие таково: необходимо определить возраст капитана судна, если на борту находятся 26 овец и 10 козлов.
Китайские СМИ утверждают, что дети проявили неординарное мышление при решении задачи.
«Капитану минимум 18 лет, потому что в противном случае у него не было прав управлять кораблём», — заметил один из пятиклассников.
Другой посчитал, что капитан чересчур самовлюблён и взял на корабль число животных, равное его возрасту.
Взрослые, наткнувшиеся на эту задачу в интернете, тоже подошли к решению нетривиально. Так, один пользователь китайских соцсетей предложил свой вариант:
«Общий вес всех животных на борту составит 7700 кг, исходя из среднего веса каждого животного. В Китае для управления кораблём с грузом более 5 тонн необходимо обладать лицензией на протяжении пяти лет, а выдают их только с 23.
Значит, капитану минимум 28 лет».
Однако это спровоцировало новую дискуссию между пользователями. Некоторые обратили внимание на неточность в расчётах:
«Каким образом могут 26 овец и 10 коз весить 7700 кг?? Получается, коза или овца весит более 200 кг!!!»
В китайском Министерстве образования объяснили, что главной целью задания было заставить детей избавиться от шаблонного мышления, а точного ответа на вопрос не существует.
Впрочем, большинство людей возмущены не столько самой задачей, сколько тем, что её задали на уроке математики.
А вот еще одна задачка:
Подсказка: Обратите внимание: мишка в шапочке и без шапочки, автобус с мишкой и без мишки.
Правильный ответ: 9.
Поделитесь статьей с друзьями!
Оксана
Математика в Древнем Китае — Википедия
- Данная статья — часть обзора История математики
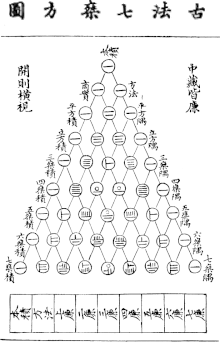
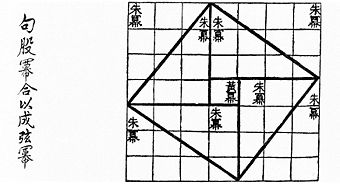Китайская версия пифагоровой тройки:3 × 4 × 5
Первые дошедшие до нас китайские письменные памятники относятся к эпохе Шан (XVIII—XII вв. до н. э.). И уже на гадальных костях XIV века до н. э., найденных в Хэнани, сохранились обозначения цифр.
Развитие науки продолжилось после того, как в XI веке до н. э. династию Шан сменила династия Чжоу. В эти годы возникают китайская математика и астрономия. Появились первые точные календари и учебники математики. «Истребление книг» императором Цинь Ши Хуаном (Ши Хуанди) не позволило ранним книгам дойти до нас, однако они, скорее всего, легли в основу последующих трудов.
С воцарением династии Хань (208 г. до н. э. — 220 г. н. э.) древние знания стали восстанавливать и развивать. Во II веке до н. э. опубликованы наиболее древние из дошедших до нас сочинений — математико-астрономический «Трактат об измерительном шесте» и фундаментальный труд «Математика в девяти книгах» ( Цзю чжан суань шу 《九章算术》). Толкование этого трактата было облегчено благодаря открытию текста «Суань шу шу[en]» 筭數書 в 1983-84 годах (Чжанцзяшань, провинция Хубэй), относящегося примерно к этому же периоду.
Математика в девяти книгах (начало)«Математика в девяти книгах» — наиболее содержательное математическое сочинение древнего Китая. Это слабо согласованная компиляция более старых трудов разных авторов. Книга была окончательно отредактирована финансовым чиновником Чжан Цаном (умер в 150 году до н. э.) и предназначена для землемеров, инженеров, чиновников и торговцев. В ней собраны 246 задач, изложенных в традиционном восточном духе, то есть рецептурно: формулируется задача, сообщается готовый ответ и (очень кратко и не всегда) указывается способ решения.
Цифры обозначались специальными иероглифами, которые появились во II тысячелетии до н. э., и начертание их окончательно установилось к III в. до н. э. Эти иероглифы применяются и в настоящее время. Китайский способ записи чисел изначально был мультипликативным. Например, запись числа 1946, используя вместо иероглифов римские цифры, можно условно представить как 1М9С4Х6. Однако на практике расчёты выполнялись на счётной доске суаньпань, где запись чисел была иной — позиционной, как в Индии, и, в отличие от вавилонян, десятичной[1].
Китайские (вверху) и японские счётыКитайская счётная доска по своей конструкции аналогична русским счётам. Нуль сначала обозначался пустым местом, специальный иероглиф появился около XII века н. э. Для запоминания таблицы умножения существовала специальная песня, которую ученики заучивали наизусть.
Приближение дробями числа π{\displaystyle \pi } Вписанный круг Ли Е в треугольник: Схема круглого города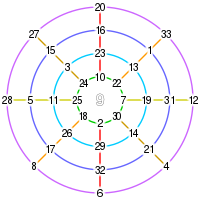
Престиж математики в Китае был высок. Каждый чиновник, чтобы получить назначение на пост, сдавал, помимо прочих, и экзамен по математике, где обязан был показать умение решать задачи из классических сборников.
В I—V вв. н. э. китайцы уточняют число π{\displaystyle \pi } — сначала как 10{\displaystyle {\sqrt {10}}}, потом как 142/45 = 3,155…, а позже (V век) как 3,1415926, причём открывают для него известное рациональное приближение: 355/113.
В это время китайцам уже было известно многое, в том числе:
Был даже разработан метод фан-чэн (方程) для решения систем произвольного числа линейных уравнений — аналог классического европейского метода Гаусса.
В области геометрии им были известны точные формулы для определения площади и объёма основных фигур и тел, теорема Пифагора и алгоритм подбора пифагоровых троек.
В III веке н. э., под давлением традиционной десятичной системы мер, появляются и десятичные дроби. Выходит «Математический трактат» Сунь-Цзы. В нём, помимо прочего, впервые появляется задача, которой позднее в Европе занимались крупнейшие математики, от Фибоначчи до Эйлера и Гаусса: найти число, которое при делении на 3, 5 и 7 даёт соответственно остатки 2, 3 и 2. Задачи такого типа нередки в теории календаря.
Другие темы исследования китайских математиков: алгоритмы интерполирования, суммирование рядов, триангуляция.
- История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Березкина Э. И. Математика древнего Китая. М., 1980.
- Березкина Э. И. Древнекитайская математика. М., 1987.
- Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.
- Депман И. Я. История арифметики. Пособие для учителей. — Изд. второе. — М.: Просвещение, 1965. — 416 с.
- Кобзев А. И. Учение о символах и числах в китайской классической философии. М., 1994.
- Рыбников К. А. История математики. М., 1994.
- Хрестоматия по истории математики. Арифметика и алгебра. Теория чисел. Геометрия / Под ред. А. П. Юшкевича. М., 1976.
- Волков А. К. О доказательстве в древнекитайской математике (тезисы)// XV научная конференция «Общество и государство в Китае». М.,1984.Ч.1. С.101-104.
- Волков А. К. Доказательство в древнекитайской математике //Методологические проблемы развития и применения математики. М., 1985.С.200-206.
- Волков А. К. Вычисление площадей в Древнем Китае.// Историко-математические исследования. Вып.29. М.,1985. С.28-43.
- Волков А. К. О геометрическом происхождении древнекитайского метода извлечения квадратных и кубических корней. // История и культура Восточной и Юго-Восточной Азии. М., 1986.
- Володарский А. И. Математические связи Индии и Китая в древности и в средние века // Годичная научная конференция Института истории естествознания и техники РАН, 1995. М., 1996.
- Глебкин В. В. Наука в контексте культуры («Начала» Евклида и «Цзю чжан суань шу»)М.,1994.192 с.
- Жаров В. К. О «Введении» к трактату Чжу Шицзе «Суань сюе ци мэн» // Историко-математические исследования. Вторая серия. Выпуск 6(41).М., 2001. С.347-353.
- Т. Хуан О древнекитайском трактате «Математика в девяти книгах» в русском переводе, УМН, 1958, 13:5(83), 235—237.
- Mikami Y. The development of mathematics in China and Japan. Leipzig, 1913.
- Needham, Joseph Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd. 1986.
- Lam Lay Yong, Ang Tian Se. Fleeting Footsteps.Tracing the concept of the arithmetic and algebra in ancient China. Singapore,1992.
Математическое образование в Шанхае: трудолюбие и отвага / Newtonew: новости сетевого образования
А вот Россия наоборот, каждые три года опускается в рейтинге PISA всё ниже.
Результаты PISA 2012. Инфографика: Финбар Шии. Источник: theguardian.com
В России качеством математического образования озабочены уже несколько лет, и совсем недавно этот вопрос снова поднимался в комитете Государственной думы по вопросам образования.PISA, международная программа оценки знаний, последний раз была проведена в 2012 году — то самое время, когда большинство из 65 стран-участниц переживало последствия экономического кризиса и ясно осознавало необходимость получения молодёжью новых навыков. Но на результатах восточно-азиатских стран кризис не сказался совсем.
Лидеры по результатам PISA 2012. Инфографика: Финбар Шии. Источник: theguardian.com
Эти результаты привлекли пристальное внимание мировой общественности и экспертов в образовании. Так, например, бывший заместитель премьер-министра Канады Джон Мэнли тогда назвал проблему обучения математике «общенациональной проблемой»; а Великобритания с лёгкой руки министра образования Элизабет Трасс готовится принять в свои школы десятки китайских учителей в попытке улучшить качество математического образования в своей стране.
Но вычислить все компоненты успеха Китая в математическом образовании практически невозможно, ведь полученный результат зависит не только от методологии образования, но и от культурной среды.
Некоторые считают, что ошеломительный успех Шанхая в результатах PISA связан с распространённой в стране практике агрессивной зубрёжки и механического запоминания.
Но есть неоспоримое опровержение этому мнению: шанхайские студенты показали наиболее впечатляющие результаты не в тех заданиях, в которых требовалось лишь воспроизведение своих знаний, а в тех, которые были нацелены на более широкое и творческое применение навыков. Концептуализация, генерализация и творческий подход — это наивысшие показатели, требуемые системой PISA.
Другие объясняли успех Шанхая исключением из результатов сравнения угнетённых слоёв внутренних мигрантов. Однако внутренние мигранты всегда были участниками тестов PISA в Шанхае, и многие образовательные системы Восточной Азии превосходят западные как раз благодаря своей способности поднять академический потенциал молодёжи из угнетённых слоёв населения.
В Восточной Азии самые талантливые учителя работают не с самыми талантливыми детьми, а с самими сложными. В то время как американская мечта о социальном лифте становится всё более расплывчатой, в азиатском обществе она становится реальностью.
Если говорить о системе образования как о системе принципов и опыта, которые можно перенять, стоит отметить, что невозможно просто скопировать успешную систему и ждать результатов — социокультурную, историческую и экономическую разницу необходимо принимать во внимание. Однако результаты PISA обнажили некоторое количество отличительных черт самых успешных образовательных систем в мире, о которых стоит поговорить. Например, лидеры мнений в Восточной Азии смогли убедить своих граждан делать выбор в сторону получения знаний, а не материальной выгоды. И это — лишь одна из переменных сложного уравнения под названием «работающая образовательная система».
Встреча Востока и Запада. Художник: Шиба Кокан. Источник: Википедия
Головокружительная свобода в школах и большие надежды родителей
Ресурс Theglobeandmail побывал на нескольких уроках математики в одной из шанхайских школ и поговорил с опытными шанхайскими профессорами и педагогами.
Лао Кайшэн, профессор Университета Кэпитал Нормал в Пекине, говорит:
Китайские работники образования сейчас стремятся перенять элементы западного образования, чтобы поднимать дух учеников и помогать им расти в дружелюбной и счастливой обстановке.
В отличие от большинства китайских образовательных учреждений, в Шанхае разрешается пользоваться калькуляторами на вступительных экзаменах.
И действительно, в шанхайских школьных кабинетах — по крайней мере, в тех, которые с удовольствием показывают западным гостям, математика ощущается как крайне увлекательная наука.
Вот ведёт урок в начальной школе тихого спального района миссис Ни. Она спрашивает своих восьми- и девятилетних подопечных:
— Вы любите шашки?
— Да-а-а-а!
На экране появляется интерактивное изображение доски с шашками. Учительница с помощью всего класса выигрывает партию белыми.
После этого с помощью проектора миссис Ни показывает детям карту Китая от National Geographic с обозначенным звёздочкой Пекином. Здесь их дом. Но это не просто точка на карте, объясняет учительница, это отметка в системе координат: 31,2° северной широты, 121,4° восточной долготы. Здесь действуют такие же пары чисел, как и при совершении ходов в шашках, и именно так учёные изобрели GPS, которым вы пользуетесь на своих телефонах.
Учителя стараются снизить нагрузку на учеников. В начальной школе, в которой преподаёт миссис Ни, ученики пятого класса вполне могут в качестве домашнего задания программировать, играть на пианино или ударных. Родители довольны:
Современные дети не будут зубрить. Когда мы были детьми, нас заставляли учиться родители. У сегодняшних детей свой взгляд. Вообще мне кажется, что китайские семьи стараются воспитать в своих детях прежде всего чувство прекрасного.
Один из примеров успеха такого подхода — юный Гу Чао, золотой медалист международной математической олимпиады 2013 года. Он посещал школу с языковым уклоном, а его мама признаётся, что математикой Гу Чао всегда занимался сам.
При этом нагрузка на детей со стороны родителей остаётся велика, возможно, именно поэтому в китайских школах продвигается концепция дружелюбной атмосферы и снижение объёма домашней работы. В китайской культуре ребёнок — это предмет гордости и славы для родителей и их поддержка в старости. В математических олимпиадах китайские дети начинают участвовать уже с младших классов. Всё благодаря социальному лифту — именно образование остаётся в Китае основным способом подняться по социальной лестнице.
Гу Хун-да, преподаватель математики с 50-летним стажем, говорит:
Математика крайне тесно связана с жизнью, наукой, технологией и экономикой, а также с тем, как мы используем инструменты для решения проблем во всех этих сферах… Шанхай как развитый китайский город стал идеальным мостом между математикой и реальной жизнью.
Мистер Гу начинал простым учителем математики, затем работал директором школы, затем возглавлял отдел образовательных исследований, а потом стал президентом местного педагогического колледжа. Сам он был студентом ещё до коммунистической революции, и всю жизнь проработал в образовательной системе.
Среди его учебных материалов — фотографии мостов и небоскрёбов, упражнения по тригонометрии, которые помогают отрисовать логотип МакДоналдса или рассчитать высоту известной шанхайской «Восточной жемчужины».
Источник: pixabay.com
Трудолюбие как залог таланта
Ещё одной гранью успеха эффективности азиатской образовательной системы является вера в способности абсолютно всех детей. В Японии, к примеру, студенты не только верят в то, что они являются хозяевами своей судьбы, но и готовы принимать на себя ответственность за свои действия: 84% японских студентов говорят, что их не отпугивают сложные проблемы; в США такую же степень ответственности готовы на себя взять только 50% опрошенных.
Тот факт, что азиатские студенты верят в то, что достигнуть значимых результатов возможно только посредством тяжёлого труда, а не врождённых способностей, косвенно свидетельствует о том, что образовательная система и социальная среда весьма способствуют внедрению представления о ценности стараний.
Время, когда всех студентов учили одинаково, прошло. Шанхай реализует дифференцированный подход к обучению; шанхайские учителя многое ожидают от каждого ученика и признают, что самые обычные учащиеся обладают необычными способностями.
Особую роль играет прозрачность системы: все участники системы знают все требования, которым необходимо соответствовать для получения нужного уровня квалификации.
Пионерка на еженедельной церемонии поднятия флага в Восточной экспериментальной школе Шанхая, 5 ноября 2012 г. Источник: time.com
Учителя как краеугольный камень системы
Не существует такой образовательной системы, качество которой не зависело бы от педагогического таланта и подготовки своих учителей.
Восточно-азиатские системы школьного образования тщательно следят за отбором и обучением своих педагогических ресурсов. Когда решается вопрос о распределении бюджета и инвестиций, приоритет отдаётся не расширению классных площадей, а повышению качества подготовки учителей. Не последнюю роль в процессе играет и предоставление многочисленных возможностей для повышения педагогической квалификации.
Лучшие представители педагогической отрасли в азиатских странах стремятся отойти от бюрократического контроля и отчётности, заменив их более совершенными формами организации работы. Учительское дело ценится прежде всего за инновационный подход, повышение личной эффективности и собственное профессиональное развитие и оказанную помощь коллегам.
Опыт Шанхая: в городе регулярно проводятся общегородские семинары с лучшими учителями города; в каждой школе еженедельно проходят и внутренние семинары, где опытные учителя математики делятся своими наработками с более молодыми коллегами. Процесс повышения квалификации учителей жёстко регламентирован: учителя средней категории каждые 5 лет должны проходить 240 часов курса повышения квалификации; учителя высшей категории — 540 часов (включая 300 часов научно-исследовательской работы). Если квалификация учителя не дотягивает до определённого уровня, он теряет работу.
Проблемы остаются
Среди проблем, которые называют китайские эксперты в области образования, остаются всё те же, знакомые и западным странам: экзаменационная система и снижение интереса к математике в высшей школе.
Экзаменационная политика в Китае проверяет ограниченный набор критериев — уровень запоминания и восприятия; коммуникативные и творческие навыки остаются за бортом.
Ранняя мотивация к математическим наукам порой оборачивается другой стороной медали: дети, блестяще сдающие тесты в младшей/средней школе и на вступительных экзаменах, теряют интерес к математике на протяжении институтского курса. Математическое образование оказывается в тисках демотивированности.
Ценностями образования прошлого были стандартизация и соответствие этим стандартам; сейчас на первый план выходит изобретательность. В прошлом внимание уделялось самому факту предоставления образования; в лучших образовательных системах мира акцент ставится на результатах образования, на выходе за рамки бюрократии, на построение крепких связей с коллегами, другими школами, на построении профессиональной сети. Это очень заметно в образовательных системах Финляндии и Японии.
Успешную образовательную систему от неуспешной отличает её способность предоставить высокое качество на всех уровнях системы. Действующая политика образования и наиболее эффективные практики распространяются на все аспекты системы. Это — образовательный подход Сингапура.
Современный мир перестаёт быть жёстко скованным традициями, старается отойти от привычного и немилосерден к устаревшему. Успех приходит к тем, кто легко адаптируется, не жалуется на тяжёлую работу и открыт к переменам — будь то отдельный человек, компания или целая страна.
По материалам cnn.com, theglobeandmail.com
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.
Китай: математика для дошкольников: malyshi — LiveJournal
- who_stole_tarts (who_stole_tarts) wrote in malyshi,
Расскажу немного о детсадовских прописях и покажу, сколько занимательных примеров можно придумать из цифр от 0 до 9 только с помощью бумаги и ручки для ребенка, который совсем не умеет писать.
Ну во-первых, у китайцев есть свои письменные (знаками) и устные (на пальцах) обозначения цифр. Но прописей по математике это не касается, там все цифры арабские.
Во-вторых, в китайской иероглифике нет окружностей, да и просто круглых линий не много.
В-третьих, многие пары китайских иероглифов отличаются друг от друга всего лишь тем, доходит одна из линий до пересечения с другой, или нет. Это смыслоразличительная особенность: не заметив этого нюанса, можно перепутать слова с совершенно разным смыслом. Поэтому даже очень неаккуратные китайцы с неразборчивым почерком:) критично оценивают пересечения линий в символах.
Ну так вот. Сначала разберу по особенностям наиболее показательную работу.
1) Задача была оценить, насколько кружочков меньше, чем треугольников, и насколько квадратиков больше, чем треугольников. Мамин мехмат ситуацию не спас, иероглифы вовремя не раскодировали и ответ посчитали неверно:)
2) В связи с особенностью пересечений линий все китайцы пишут 4, отрывая руку — с обязательным перечеркиванием вертикальной линии. Нашу 4 они воспринимают как 9 (даже не замкнутую сверху), поэтому учитель зачеркивает мой ответ 4 и пишет сверху 4. Потом, видимо, понимает — и ставит знак «правильно».
3) Еще особенности написания цифр. 6 и 9 — почти без круглого хвостика, 7 не перечеркнута, единичка одной палочкой. Цифра 8 им вообще дается довольно сложно с учетом округлых форм.
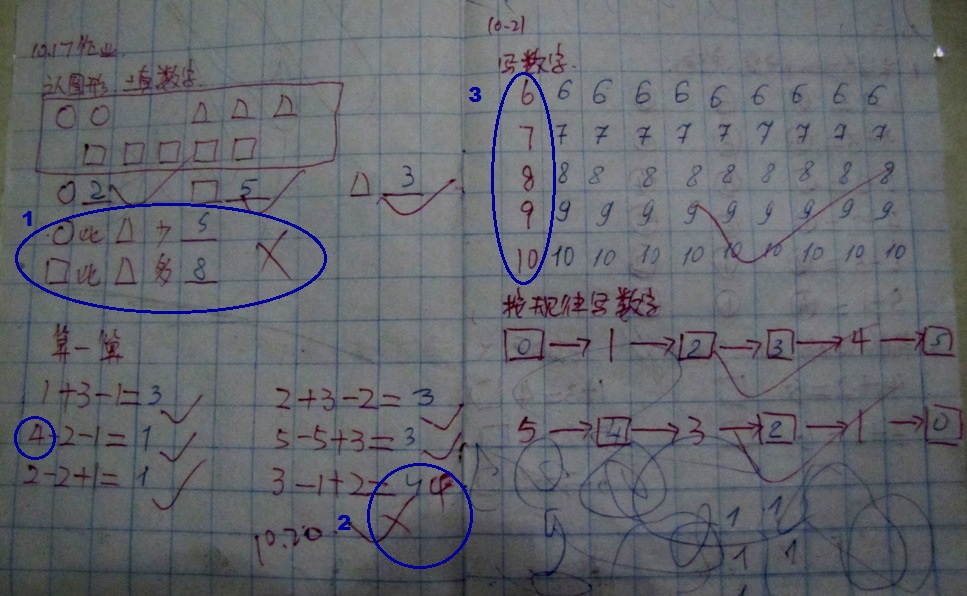
А дальше просто набор задач. Воспитатель самого обыкновенного районного садика каждый раз придумывает разные записи примера специально для нашего 2-летнего ребенка, который еще не умеет писать (в отличие от пятилеток-одноклассников). Предлагаю заинтересовавшимся родителям попробовать на малышах дошкольниках отрабатывать навыки счета подобными способами. Мы все примеры сначала отрабатываем на машинках-карандашах, а потом уже прорисовываем ответ (цифры, естественно, за ребенка пишет мама).
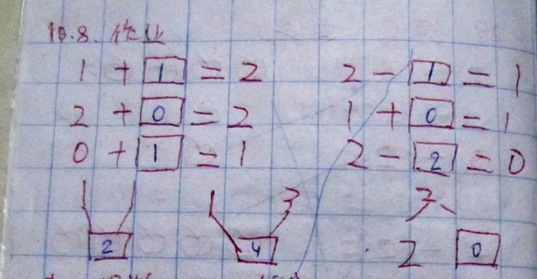
Photo
Hint http://pics.livejournal.com/igrick/pic/000r1edq
Про китайские счеты и китайскую математику
Счет на китайских счетах в конце прошлого года внесен в список ЮНЕСКО. Как нематериальное культурное наследие. Прикиньте, какой это был прорыв в свое время — счеты. А я вот, к примеру, в раннем детстве использовала счеты как коляску для своих кукол…
Можете не верить: способ вычислений с помощью китайских счет — в том же ряду, что и изобретение ими компаса, бумаги, пороха и т.п.
На каком-то этапе китайцы включили этот математический способ в почетный список на национальном уровне.
Потом дело дошло до ЮНЕСКО.
Я еще, кстати, захватила то время, когда наши магазинные продавцы-кассиры ловко гоняли костяшки на счетах.
Хотя, вроде, их счеты и китайские несколько отличались.
Но тем не менее: судя по всему, счеты пошли именно оттуда.
Как и вообще само понятие СЧЕТ.
Если источники ничего не путают, первые обнаруженные обозначения цифр относятся к Китаю периода 14 века аж до н.э.
Найдены они были в провинции Хэнань.
В 11 веке — опять же ДО н.э., — при династии Чжоу появилась математика и астрономия.
А так же учебники математики.
Были впервые опубликованы самые древние сочинения, что дошли до нас — математико-астрономический «Трактат об измерительном шесте» и фундаментальный труд «Математика в девяти книгах».
Математика в 9 книгах…
Это, по большому счету, сборник старых работ разных авторов.
Причем, не слишком связанных между собой.
Окончательная редакция приписывается финансовому чиновнику Чжан Цану, который покинул сей бренный мир еще в 150 году до н.э.
В редакцию вошли 246 задач в восточном стиле: т.е. сформулирована сама задача, ответ и способ решения.
Причем, кратко, да и то не во всех случаях.
Задачи предназначались для торговцев, чиновников, землемеров и инженеров.
Иероглифы, которые обозначали цифры, появились во 2 веке до н.э.
Окончательно утвердились в 3 веке до н.э.
Судя по всему, те самые, что действуют и сегодня.
Кто ездит в Китай — очень полезно знать.
Как минимум, чтобы разобраться в китайских ценниках.
Говорят, китайские счеты очень похожи на наши, русские.
Те самые, которыми и пользовались еще недавно наши бухгалтера и кассиры.
Математика в древнем Китае
Еще с древних времен она высоко ценилась в этой стране.
Каждый чиновник, чтобы получить заветное кресло, обязан был в числе прочих экзаменов сдавать и экзамен по математике.
Уже во времена нашей эры — 1-5 веках, — китайцы открывают, что такое пропорции, а так же математические действия с дробями.
Квадратные уравнения и математические действия с отрицательными числами.
К слову, эти самые числа подразумевались как долги.
…Я вот порылась в разных источниках.
Честно признаюсь — сама с математикой не очень дружила в школе и профессия у меня, нисколько не математическая.
Хотя математику уважаю, а сейчас (т.е. когда порылась) многие вещи звучат завораживающе.
Например, в том же периоде начала нашей эры появился метод (фан-чэн), который позволял решать системы произвольного числа линейных уравнений.
Позднее в Европе появился известный сегодня метод Гаусса.
Насколько позднее — я пока не нашла.
А еще в Китае, если опять же, верить истории, решение уравнений любой степени методом тянь-юань (天元术) очень напоминает сегодняшний метод Руффини-Горнера для нахождения корней многочлена.
…Еще с древней древности китайцы знали каким-то странным образом формулы площади и объема главных фигур и тел.
А еще теорему Пифагора и алгоритм подбора пифагоровых троек.
…Примерно в 3 веке НАШЕЙ эры в Китае становится известны десятичные дроби.
Вскоре появляется Математический трактат Сунь-Цзы — китайского математика и астронома.
Его время жизни точно не известно — называется период с 3 по 5 века н.э.
В трактате появляется задача, над которой гораздо позже бились крупнейшие математики Европы:
найти число, которое при делении на 3, 5 и 7 даёт соответственно остатки 2, 3 и 2
Для тех, кто в этом мало что понимает (вроде меня), добавлю: подобные задачи нередко применяются в теории календаря.