Арифметика что это такое: Арифметика — это… Что такое Арифметика? – Арифметика — Википедия. Что такое Арифметика

Изучаем арифметику онлайн, математические игры и упрощенные приемы

Что такое арифметика? Арифметика – раздел математики, работающий с числами и вычислениями (действиями с числами).

Арифметику начинают изучать в начальной школе, потому что это основа математики, там изучаются основные операции с числами: сложение, вычитание, умножение, деление.

Арифметика – самый основной, базовый раздел математики. Возникновению она обязана потребностям людей в счете.

Ментальная арифметика

Что называется ментальной арифметикой? Ментальная арифметика – это метод обучения быстрому счету, пришедший из древности.

В настоящее время, в отличии от предыдущего, преподаватели стараются не только обучить детей скорости счета, но и стараются развить мышление.

Сам процесс обучения строится на использовании и развитии обоих полушарий мозга. Главное – уметь их использовать вместе, потому что они дополняют друг друга.

Действительно, левое полушарие отвечает за логику, речь и рациональность, а правое – за воображение.

В программу обучения входит обучение работы и использование такого инструмента, как абакус.

Абакус – главный инструмент в изучении ментальной арифметики, потому что ученики учатся работать с ними, перебирать костяшки и осознавать суть счета. Со временем абакус стает вашим воображением, а обучаемые представляют их, опираются на эти знания и решают примеры.

Отзывы о данных методах обучения весьма положительные. Есть один минус – обучение платное, а его позволить могут не все. Поэтому путь гения зависит от материального положения.

---

Математика и арифметика

Математика и арифметика тесно связанные понятия, а вернее арифметика – раздел математики, работающий с числами и вычислениями (действиями с числами).

Арифметика – основной раздел, а значит и основа математики. Основа математики – важнейшие понятия и операции, составляющие базу, на которой строятся все последующие знания. В число главных операций входят: сложение, вычитание, умножение, деление.

Арифметика, как правило, изучается в школе с самого начала обучения, то есть. с первого класса. Дети осваивают базу математики.

Сложение – это арифметическое действие, в процессе которого складываются два числа, а их результатом будет новое – третье.

Формула сложения выражается так: a + b = c.

Вычитание – это арифметическое действие, в процессе которого из первого числа вычитается второе число, а итогом будет третье.

Формула сложения выражается так: a — b = c.

Умножение – это действие, в итоге которого находится сумма одинаковых слагаемых.

Формула такого действия имеет вид: a1+a2+…+an=n*a.

Деление– это разбивание на равные части какого-либо числа или переменной.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

---

Обучение арифметике

Обучение арифметике производится в стенах школы. С первого класса дети начинают изучение базового и главного раздела математики – арифметики.

Сложение чисел

Сложение – это сумма двух или нескольких чисел. Например, 2 + 3 = 5, и графически это можно представить так:

Большие число делиться на части, возьмем число 1234, а в нем: 4-единицы, 3-десятки, 2-сотни, 1-тысячи. Итак, если мы прибавляем 4 к 7, то 4+7=10+1, то есть 1 десяток и 1 единица. Если складывая числа в одном разряде (единицах, например) у вас число больше 10, но меньше 20, то в десяток вы добавляете единицу, а остальное оставляете на месте единиц.

Еще один пример: 8+9, получаем 10+7, значит в десятки мы добавляем 1, а на место единиц записываем 7, получаем 17.

Вычитание чисел

Вычитание – обратная операция сложению. Например, из 6 нужно вычесть 5. 6-5=1, 6 больше числа 5 на единицу, значит, и ответ будет единицей. Можно для проверки произвести сложение 1+5=6.

Большое число делится на части, возьмем число 1234, а в нем: 4-единицы, 3-десятки, 2-сотни, 1-тысячи. Если вычитать единицы, то все легко и просто. Но допустим пример: 14 — 7. В числе 14: 1 – десяток, а 4 – единицы. Один десяток – 10 единиц. Тогда получаем 10 + 4 — 7, сделаем так: 10 — 7 + 4, 10 — 7 = 3, а 3 + 4 = 7. Ответ найден верно!

Рассмотрим пример 23 — 16. Первое число 2 десятка и 3 единицы, а второе 1 десяток и 6 единиц. Представим число 23 как 10 + 10 + 3, а 16 как 10 + 6, тогда представим 23 — 16 как 10 + 10 + 3 — 10 — 6. Тогда 10 — 10 = 0, останется 10 + 3 — 6, 10 — 6 = 4, тогда 4 + 3 = 7. Ответ найден!

Аналогично делается с сотнями и тысячами/

Умножение чисел

Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.

Пример 2*5. Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.

Пример 4*3. Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.

Пример 5*3. Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.

Деление чисел

Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение. 3*3=9. Верно? Абсолютно.

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Ускоряем устный счет, НЕ ментальная арифметика

Научитесь быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

---

Правила арифметики

Порядок выполнения операций в выражении – очень важен!

Если пример имеет вид 2+3-4, то порядок в нем может быть каким угодно. Потому что операции сложения и вычитания имеют одинаковый приоритет. Если выполним сначала сложение, то получим: 5-4=1, а если сначала вычитание, то: 2-1=1. Как видите результат одинаковый.

Аналогично с выражением умножения и деления. Операции умножения и деления имеют одинаковый приоритет. Например, 28:4. Выполним сначала умножение: 16:4=4, а если деление: 22=4.

Порядок имеет смысл, когда в выражении смешиваются операции сложения или вычитания, с операциями умножения или деления. Например:

2+22. Первым действием выполняются ВСЕ операции умножения и деления, а только потом сложения и вычитания. То есть выражение 2+22 = 2+4=6.

Но в выражениях присутствуют скобки. Скобки имеют свойство менять порядок операций. Рассмотрим предыдущий пример, только со скобками: (2+2)*2. В таком случае сначала выполняются операции в скобках, а затем вне скобок в порядке: 1. Умножение и деление 2. Сложение и вычитание.

Так, (2+2)2=42=8.

Как вы могли убедиться на примерах, скобки имеют роль. И порядок операций так же.

Уроки арифметики

Уроки арифметики – школьные уроки, вплоть до шестого класса. Дальше математика открывает свои разделы: геометрия и алгебра, а позже и тригонометрия.

Подробно об операциях вы можете прочитать в наших статьях:

1. сложение

2. вычитание

3. умножение

4. деление

Арифметика 5 класс

В пятом классе школьник начинают изучение таких тем как: дробные числа, смешанные числа. Информацию про операции с этими числами вы можете найти в наших статьях по соответствующим операциям.

Дробное число – это отношение двух чисел друг к другу или же числителя к знаменателю. Дробное число можно заменить операцией деления. Например, ¼ = 1:4.

Смешанное число – это дробное число, только с выделенной целой частью. Целая часть выделяется при условии, что числитель больше знаменателя. Например, была дробь: 5/4, ее можно преобразовать, путем выделения целой части: 1целая и ¼.

Примеры для тренировки:

Задание №1:

Задание №2:

Арифметика 6 класс

В 6ом классе появляется тема преобразования дробей в строчную запись. Что это значит? Например, дана дробь ½, она будет равна 0,5. ¼ = 0.25.

Примеры могут составляться в таком стиле: 0.25+0.73+12/31.

Примеры для тренировки:

Задание №1:

Задание №2:

Игры для развития устного счета и скорости счета

Существуют прекрасные игры, способствующие развитию счета, помогающие развивать математические способности и математическое мышление, устный счет и скорость счета! Можно играть и развиваться! Вам интересно? Прочтите краткие статьи об играх и обязательно попробуйте себя.

Игра «Быстрый счет»

Игра «быстрый счет» поможет вам ускорить устный счет. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ да или нет на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Играть сейчас

Игра «Математические сравнения»

Игра «Математические сравнения» потребует от вас сравнения двух чисел на время. То есть вам предстоит выбрать как можно быстрее одно из двух чисел. Помните, что время ограничено, а чем больше вы ответите верно, тем лучше будут развиваться ваши математические способности! Попробуем?

Играть сейчас

Игра «Быстрое сложение»

Игра «Быстрое сложение» — отличный тренажер быстрого счета. Суть игры: дано поле 4×4, то есть. 16 чисел, а над полем семнадцатое число. Ваша цель: при помощи шестнадцати чисел составить 17, пользуясь операцией сложения. Например, над полем у вас написано число 28, то в поле вам надо найти 2 таких числа, которые в сумме дадут число 28. Вы готовы попробовать свои силы? Тогда вперед, тренироваться!

Играть сейчас

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

---

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

---

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.

После прохождения курса ребенок сможет:

1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова
2. Научится запоминать на более длительный срок
3. Увеличится скорость воспоминания нужной информации

---

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

---

Как улучшить память и развить внимание

Бесплатное практическое занятие от advance.

---

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Определение арифметика общее значение и понятие. Что это такое арифметика

Прежде чем полностью перейти к разъяснению значения термина арифметика, мы проанализируем его этимологическое происхождение. В частности, можно сказать, что это слово происходит от латинского существительного arithmetica. Тем не менее, это, в свою очередь, происходит от греческого, а именно «aritmetikos», который является результатом суммы двух разных частей:
-Имя «арифмос», которое можно перевести как «число».
Суффикс «-tikos», который используется для обозначения «по отношению к».

Арифметика — это область математики, сосредоточенная на числах и операциях, которые выполняются с ними. Следует помнить, что числа являются знаками, которые позволяют выразить количество.

Формальное появление арифметики имело место в Древней Греции из-за увеличения строгости математики и развития демонстраций. Таким образом, были установлены четыре элементарных операции этой ветви:

сложение, вычитание, умножение и деление .

Продвигаясь по сложности арифметики, можно переходить от элементарных операций к другим, таким как извлечение корней и вычисление мощности . Также возможно включить буквы рядом с числами, чтобы достигнуть представления различных переменных.

Среди наиболее важных фигур в арифметике в Древней Греции мы можем выделить такие, как следующие:
Евклид (325 г. до н.э. — 265 г. до н.э.), который считается отцом геометрии. Он сделал многочисленные работы, которые стали столпами вышеупомянутой арифметики, как в случае с «Элементами».
-Нормамак Герасы, который указан как математик neopitagórico. Одной из его наиболее важных и признанных работ была «Введение в арифметику», где, помимо прочего, выходит на стол и хорошо объясняется теория чисел. Настолько важной была та работа, которая стала ручной в платоновских школах.

Арифметические расчеты могут развиваться по-разному. Если это простые операции, их можно сделать мысленно или с помощью пальцев руки. В древние времена также использовалась абака, устройство с маленькими шариками, которые перемещаются, чтобы делать вычисления. В настоящее время арифметические операции обычно выполняются с помощью калькулятора, физического или виртуального.

Хотя верно, что счеты являются одним из самых известных инструментов, которые использовались для выполнения вычислений в рамках арифметики, в истории они существовали, и есть много других с той же целью. Мы имеем в виду счетные палочки, вавилонскую табличку, счеты инков, сумматор …

Это известно как высокая арифметика для изучения свойств и функций чисел. В этом контексте мы можем говорить о двоичной арифметике (которая обращается к нулю и единице для представления значений ), модульной арифметике

(которая работает с модулями) и порядковой арифметике (ориентированной на порядковые числа) и других.

Арифметика второго порядка, с другой стороны, состоит из различных аксиоматических систем, которые допускают формализацию натуральных чисел и образованных ими подмножеств.

Определение арифметика общее значение и понятие. Что это такое арифметика

Прежде чем полностью перейти к разъяснению значения термина арифметика, мы проанализируем его этимологическое происхождение. В частности, можно сказать, что это слово происходит от латинского существительного arithmetica. Тем не менее, это, в свою очередь, происходит от греческого, а именно «aritmetikos», который является результатом суммы двух разных частей:
-Имя «арифмос», которое можно перевести как «число».
Суффикс «-tikos», который используется для обозначения «по отношению к».

Арифметика — это область математики, сосредоточенная на числах и операциях

, которые выполняются с ними. Следует помнить, что числа являются знаками, которые позволяют выразить количество.

Формальное появление арифметики имело место в Древней Греции из-за увеличения строгости математики и развития демонстраций. Таким образом, были установлены четыре элементарных операции этой ветви: сложение, вычитание, умножение и деление .

Продвигаясь по сложности арифметики, можно переходить от элементарных операций к другим, таким как извлечение корней и вычисление мощности . Также возможно включить буквы рядом с числами, чтобы достигнуть представления различных переменных.

Среди наиболее важных фигур в арифметике в Древней Греции мы можем выделить такие, как следующие:
Евклид (325 г. до н.э. — 265 г. до н.э.), который считается отцом геометрии. Он сделал многочисленные работы, которые стали столпами вышеупомянутой арифметики, как в случае с «Элементами».

-Нормамак Герасы, который указан как математик neopitagórico. Одной из его наиболее важных и признанных работ была «Введение в арифметику», где, помимо прочего, выходит на стол и хорошо объясняется теория чисел. Настолько важной была та работа, которая стала ручной в платоновских школах.

Арифметические расчеты могут развиваться по-разному. Если это простые операции, их можно сделать мысленно или с помощью пальцев руки. В древние времена также использовалась абака, устройство с маленькими шариками, которые перемещаются, чтобы делать вычисления. В настоящее время арифметические операции обычно выполняются с помощью калькулятора, физического или виртуального.

Хотя верно, что счеты являются одним из самых известных инструментов, которые использовались для выполнения вычислений в рамках арифметики, в истории они существовали, и есть много других с той же целью. Мы имеем в виду счетные палочки, вавилонскую табличку, счеты инков, сумматор …

Это известно как высокая арифметика для изучения свойств и функций чисел. В этом контексте мы можем говорить о двоичной арифметике (которая обращается к нулю и единице для представления значений ), модульной арифметике (которая работает с модулями) и порядковой арифметике (ориентированной на порядковые числа) и других.

Арифметика второго порядка, с другой стороны, состоит из различных аксиоматических систем, которые допускают формализацию натуральных чисел и образованных ими подмножеств.

что это такое и где применяется

В математике модульная арифметика представляет собой систему расчета для целых чисел, при помощи которой они «переворачиваются» при достижении определенного значения — модуля (или множественного числа оных). Современный подход к этому виду науки был развит Карлом Фридрихом Гауссом в его книге Disquisitiones Arithmeticae, опубликованной в 1801 году. Этим методом очень любят пользоваться специалисты по информатике, поскольку это очень интересно и открывает определенные новые возможности в операциях с числами.

Суть

Поскольку число часов начинается заново после того, как оно достигает 12, это арифметическое по модулю 12. Согласно приведенному ниже определению 12 соответствует не только 12, но и 0, поэтому можно также назвать время, называемое «12:00». «0:00». Ведь 12 совпадает с 0 по модулю 12.

Модульная арифметика может обрабатываться математически, путем введения конгруэнтного отношения к целым числам, которое совместимо с операциями над целыми числами: сложение, вычитание и умножение. Для положительного целого числа n два числа a и b называются конгруэнтными по модулю n, если их разность a — b кратна n (то есть, если существует целое число k такое, что a — b = kn).

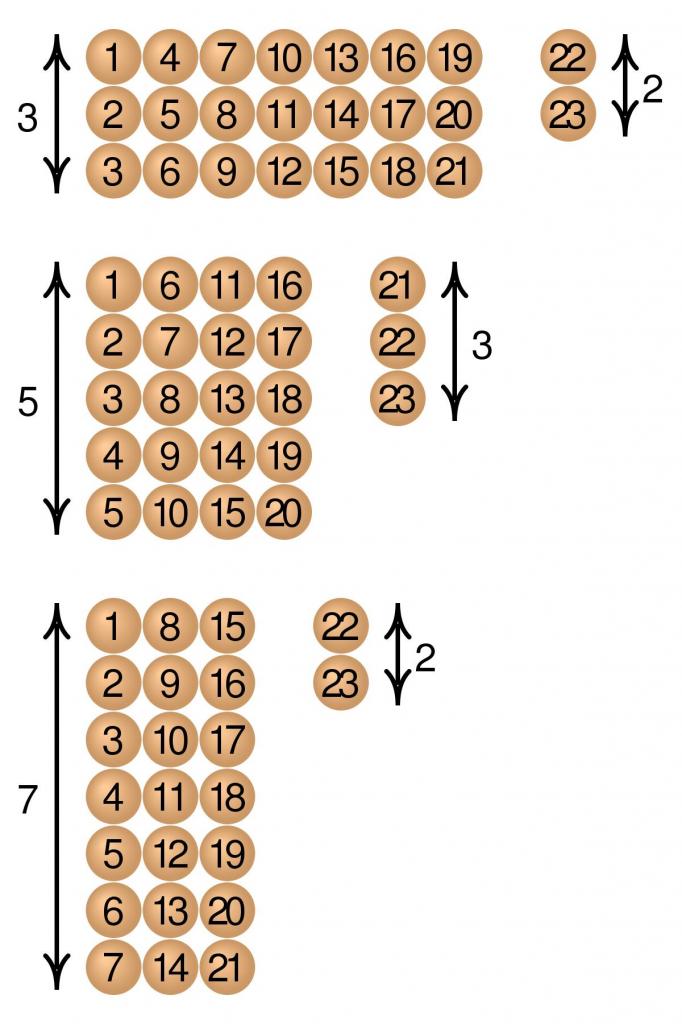
Вычеты

В теоретической математике модульная арифметика является одной из основ теории чисел, затрагивающей почти все аспекты ее изучения, а также широко используется в теории групп, колец, узлов и абстрактной алгебре. В области прикладной математики она используется в компьютерной алгебре, криптографии, информатике, химии, изобразительном и в музыкальном искусстве.

Практика

Очень практичным применением является вычисление контрольных сумм в идентификаторах серийных номеров. Например некоторые общепринятые стандарты книг используют арифметику по модулю 11 (если выпущена до 1 января 2007 г.) или по модулю 10 (если выпущена до или после 1 января 2007 г.). Аналогичным образом, например, в Международных номерах банковских счетов (IBAN). Здесь используется арифметика по модулю 97 для выявления ошибок ввода пользователем в номерах банковских счетов.

В химии последняя цифра регистрационного номера CAS (уникальный идентификационный номер для каждого химического соединения) является контрольной цифрой. Она рассчитывается путем взятия последней цифры из первых двух частей регистрационного номера CAS, умноженной на 1, предыдущую цифру 2 раза, предыдущая цифра 3 раза и т. д., складывая все это и вычисляя сумму по модулю 10.

Что такое криптография? Дело в том, что она имеет весьма сильную связь с обсуждаемой темой. В криптографии законы модульной арифметики, непосредственно, лежат в основе систем с открытым ключом, таких как RSA и Диффи-Хелльман. Здесь она предоставляет конечные поля, которые лежат в основе эллиптических кривых. Используется в различных алгоритмах симметричного ключа, включая Advanced Encryption Standard (AES), Международный алгоритм шифрования данных и RC4.

Применение

Этот способ применяется в тех областях, где нужно читать цифры. Его разработали математики, а пользуются им все, особенно специалисты по информатике. Это хорошо описано в книгах вроде «Модульная арифметика для чайников». Впрочем, ряд специалистов рекомендует не воспринимать такую литературу всерьез.

В информатике модульная арифметика часто применяется в побитовых и других операциях, включающих циклические структуры данных фиксированной ширины. Ее очень любят использовать аналитики. Операция по модулю реализована во многих языках программирования и калькуляторах. В данном случае она является одним из примеров такого применения. Сравнение по модулю, деление с остатком и прочие приемы также применяются в программировании.

В музыке арифметика по модулю 12 используется при рассмотрении системы равного темперамента из двенадцати тонов, в которой происходит эквивалентность октавы и энгармоники. Иными словами, тональности в соотношении 1-2 или 2-1 эквивалентны. В музыке и других гуманитарных дисциплинах арифметика играет довольно значимую роль, но в учебниках информатики об этом обычно не пишут.

Метод приведения девяток

Метод приведения девяток предлагает быструю проверку десятичных арифметических вычислений, выполненных вручную. Он основан на модульной арифметике по модулю 9 и, в частности, на решающем свойстве 10 10 1.

существуют и другие примеры. Арифметическое по модулю 7 используется в алгоритмах, которые определяют день недели для конкретной даты. В частности, конгруэнтность Целлера и алгоритм «Судного дня» интенсивно используют арифметику по модулю 7.

Иные области применения

О модульной арифметике в криптографии уже было сказано. В этой сфере она попросту незаменима. В более общем смысле, модульная арифметика также находит применение в таких дисциплинах, как право, экономика (например, теория игр) и другие области социальных наук. Иными словами, там, где пропорциональное разделение и распределение ресурсов играет главную роль.

Поскольку модульная арифметика имеет такой широкий спектр применений, важно знать, насколько сложно решить систему сравнений. Линейная система конгруэнций может быть решена за полиномиальное время в форме исключения Гаусса. Подробнее это описывает теорема о линейной конгруэнции. Алгоритмы, такие как редукция Монтгомери, также существуют, чтобы позволить эффективно выполнять простые арифметические операции. Например, умножение и возведение в степень по модулю n, для больших чисел. Это очень важно знать для понимания того, что такое криптография. Ведь в ней как раз работают с подобными операциями.

Конгруэнция

Некоторые операции, такие как поиск дискретного логарифма или квадратичной конгруэнции, кажутся такими же сложными, как целочисленная факторизация, и, таким образом, являются отправной точкой для криптографических алгоритмов и шифрования. Эти проблемы могут быть NP-промежуточными.

Примеры

Ниже приведены три достаточно быстрые функции C — две для выполнения модульного умножения и одна для возведения в модулярные числа для целых чисел без знака, не превышающих 63 бита, без переполнения переходных операций.

Вскоре после обнаружения целых чисел (1, 2, 3, 4, 5 …) становится очевидным, что они делятся на две группы:

• Четный: делится на 2 (0, 2, 4, 6 ..).
• Нечетное: не делится на 2 (1, 3, 5, 7…).

Почему это различие важно? Это начало абстракции. Мы замечаем свойства числа (например, четное или нечетное), а не только само число («37»).

Это позволяет нам исследовать математику на более глубоком уровне и находить отношения между типами чисел, а не конкретными.

Свойства числа

Быть «тройкой» — это просто еще одно свойство числа. Возможно, не так сразу полезно, как четное/нечетное, но оно есть. Мы можем создать правила типа «тринадцать х три вена = тринадцать» и так далее. Но это сводит с ума. Мы не можем делать новые слова все время.

Операция по модулю (сокращенно mod или «%» во многих языках программирования) является остатком при делении. Например, «5 mod 3 = 2», что означает 2 — остаток, когда вы делите 5 на 3.

При преобразовании повседневных терминов в математику «четное число» — это то, где оно равно «0 mod 2», то есть остаток равен 0 при делении на 2. Нечетное число равно «1 mod 2» (имеет остаток 1).

Четные и нечетные числа

Что такое четный х четный х нечетный х нечетный? Ну, это 0 x 0 x 1 x 1 = 0. На самом деле, вы можете видеть, умножается ли где-либо четное число, где весь результат будет равен нулю.

Хитрость модульной математики в том, что мы уже использовали ее для хранения времени — иногда ее называют «арифметикой часов».

Например: 7:00 (утра/вечера — не имеет значения). Где будет часовая стрелка через 7 часов?

Модуляции

(7 + 7) mod 12 = (14) mod 12 = 2 mod 12 [2 — это остаток, когда 14 делится на 12. Уравнение 14 mod 12 = 2 mod 12 означает, что 14 часов и 2 часа выглядят одинаково на 12-часовых часах. Они являются конгруэнтными, обозначенными знаком тройного равенства: 14 ≡ 2 mod 12.

Другой пример: сейчас 8:00. Где будет большая стрелка через 25 часов?

Вместо добавления 25 к 8, вы можете понять, что 25 часов — это просто «1 день + 1 час». Ответ прост. Итак, часы закончатся на 1 час вперед — в 9:00.

(8 + 25) мод 12 ≡ (8) мод 12 + (25) мод 12 ≡ (8) мод 12 + (1) мод 12 ≡ 9 мод 12. Вы интуитивно конвертировали 25 в 1 и добавили это к 8.

Используя часы в качестве аналогии, мы можем выяснить, работают ли правила модульной арифметики, а они работают.

Сложение/Вычитание

Допустим, два раза выглядят одинаково на наших часах («2:00» и «14:00»). Если мы добавим одинаковые х часов к обоим, что произойдет? Ну, они меняются на ту же сумму на часах! 2:00 + 5 часов ≡ 14:00 + 5 часов — оба покажут 7:00.

Зачем? Мы можем просто добавить 5 к 2 остаткам, которые оба имеют, и они продвигаются одинаково. Для всех конгруэнтных чисел (2 и 14) сложение и вычитание имеют одинаковый результат.

Труднее понять, остается ли умножение таким же. Если 14 ≡ 2 (мод 12), можем ли мы умножить оба числа и получить одинаковый результат? Давайте посмотрим, что произойдет, когда мы умножим на 3.

Ну, 2:00 * 3 × 6:00. Но что такое 14:00 * 3?

Помните, 14 = 12 + 2. Итак, мы можем сказать,

14 * 3 = (12 + 2) * 3 = (12 * 3) + (2 * 3)

Первую часть (12 * 3) можно игнорировать! Переполнение 12 часов, которое несет 14, просто повторяется несколько раз. Но кого это волнует? В любом случае мы игнорируем переполнение.

Умножение

При умножении имеет значение только остаток, то есть те же 2 часа для 14:00 и 2:00. Интуитивно понятно, что именно так я вижу, что умножение не меняет отношения с модульной математикой (вы можете умножить обе стороны модульного отношения и получить один и тот же результат).

Мы делаем это интуитивно, но приятно дать ему имя. У вас есть рейс, прибывающий в 3 часа дня. Он задерживается на 14 часов. Во сколько он приземлится?

14 ≡ 2 мод 12. Так что, стоит думать об этом как 2 часа, поэтому самолет приземлиться 5 часов утра. Решение простое: 3 + 2 = 5 утра. Это немного сложнее, чем простая операция по модулю, но принцип тот же.