Дошкольники и школьники: 1 уровень «Просто»
Дошкольники и школьники: 2 уровень «Помощь брата»
Дошкольники и школьники: 3 уровень «Помощь друга»
Дошкольники и школьники: 4 уровень «Микс формулы»
Дошкольники и школьники: 5 уровень «Анзан, сложение и вычитание без ограничений»
Дошкольники и школьники: 6 уровень «Умножение»
Дошкольники и школьники: 7 уровень «Деление»
Школьники: 8 уровень «Дроби»
Школьники: 9 уровень «Отрицательные числа»
Школьники: 10 уровень «Квадратные корни»
Дошкольники: 8-10 уровень решебник «Умножение и деление»
Краткосрочный интенсив «Простое сложение и вычитание»
Экспресс курс «Умножение»
Экспресс курс «Деление»
|
Ментальная арифметика
Ментальная арифметика
Уважаемые родители!
Мы размещаем заключительное задание. В этом году на занятиях по ментальной арифметике дети прошли несколько тем: прямое сложение и вычитание однозначных чисел; прямое сложение и вычитание двухзначных чисел; правила (формулы) «младших товарищей» для решения примеров с однозначными числами. Правила «младших товарищей» аналогично применияются и для решения примеров с двухзначными числами:
+40 = +50 -10 -40 = -50 +10 +30 = +50 -20 -30 = -50 +20 +20 = +50 -30 -20 = -50 +30 +10 = +50 -40 -10 = -50 +40 На этом ментальная арифметика не заканчивается. Существуют также правила "старших товарищей", которые применяются для решения на соробане таких примеров: 13 – 5, 21 – 8, 27 + 14, 38 + 9 и т. п. На соробане можно складывать и вычитать трехзначные числа и даже умножать.
Кроме навыков счета на занятиях ментальной арифметикой дети развивали познавательные способности: внимательность, усидчивость, зрительную и слуховую память, мелкую моторику, образное мышление и скорость мыслительных процессов, умение слушать педагога и оценивать результат своей деятельности. Эти качества помогут им успешно учиться в школе. Команда педагогов ментальной арифметики желает Вам и вашим детям удачи! Мы уверены, у Вас все получится!
Задания с 18 по 22 мая
Задание
Аудио-диктант на соробане
Аудио-диктант на память
Аудио-диктант ментально
Правило и решение примеров «Младшие товарищи» (-1) (видео)
Задание с флеш-картами пропускаем. В бланке есть строка примеров с двухзначными числами. Их можно решить на соробане двумя руками.
Особенности диктантов на память: сначала надо послушать пример, запомнить его и только затем решать на соробане.
Особенности диктантов ментально: надо представить две спицы соробана и при решении двигать пальцами обеих рук, представляя, что передвигаешь косточки на спицах единиц и десятков.
Задания с 12 по 15 мая
Задание
Аудио-диктант на соробане
Аудио-диктант на память
Аудио-диктант ментально
Правило и решение примеров «Младшие товарищи» (+1) (видео)
Задания с 27 по 30 апреля
Задание
Аудио-диктант на соробане
Аудио-диктант на память
Аудио-диктант ментально
Правило «Младшие товарищи» (-2) (видео)
Решение примеров «Младшие товарищи» (-2) (видео)
Задания с 20 по 26 апреля
Занятие на закрепление пропускаем, поэтому сразу занятие 39.
Задание
Аудио-диктант на соробане
Аудио-диктант на память
Аудио-диктант ментально
Правило «Младшие товарищи» (+2) (видео)
Решение примеров «Младшие товарищи» (+2) (видео)
Задание с 13 по 17 апреля
Задания
Аудио-диктант на соробане
Аудио-диктант на память
Аудио-диктант ментально
Правило «Младшие товарищи» (-3) (видео)
Решение примеров «Младшие товарищи» (-3) (видео)
Счёт ментально. Двухзначные числа (видео)
Задание с 6 по 12 апреля
Задания
Аудио-диктант на соробане
Аудио- диктант на память
Аудио-диктант ментально
Особенности диктантов на память: сначала надо послушать пример, запомнить его и только затем решать.
Особенности диктантов ментально: надо представить две спицы соробана и при решении двигать пальцами обеих рук, представляя, что передвигаешь косточки на спицах единиц и десятков.
Правило «Младшие товарищи» (+3) (видео)
Решение примеров «Младшие товарищи» (+3) (видео)
Онлайн-курс по ментальной арифметике «Братья». Уровень: Продолжающий
Здравствуйте, меня зовут Яна Александровна.
Я преподаватель ментальной арифметики с 2012 года, автор методических пособий, сборников примеров по ментальной арифметике, авторских методик по совершенствованию навыков счета на абакусе и ментально.
В 2018 году был создан курс «Четыре вилки, три ножа и ложка». Его цель – с помощью ментальной арифметики, скорочтения и иностранных языков развивать внимание, память, координацию движений и мышление студентов.
В 2019 году создан видеокурс «Ментальная арифметика. Ардатов» для дистанционного обучения.
С 2020 преподаю курс ментальной арифметики на английском языке.
Сейчас я преподаю ментальную арифметику, иностранные языки, скорочтение, в том числе в онлайн-формате. Занимаюсь подготовкой студентов к сдаче экзаменов, а также к поступлению в школы, ВУЗы (как в России, так и за рубежом).
Студенты, окончившие мои курсы, поступают, а затем успешно обучаются в профильных школах и ВУЗах, стажируются в иностранных компаниях.
Сейчас образовательная система претерпела кардинальные изменения, которые, к сожалению, негативно сказываются не только на самих студентах, но и на тех, кто с ними связан. Это касается и их дальнейшей профессиональной трудовой деятельности, и, конечно же, их семей.
Моя цель в преподавании абсолютно любой дисциплины – научить, а точнее, заставить человека думать и рассуждать. Это становится возможным благодаря активизации всех долей головного мозга, благодаря упражнениям по ментальной арифметике и скорочтению, а также постановке задач при коммуникации (как письменной, так и устной) на родном и иностранном языке.
Таким образом, обучая студентов, я уверена в том, что хотя бы небольшая доля специалистов в той или иной сфере станет надежной опорой будущего поколения. И, нельзя не заметить, что преподавание является обоюдно полезным, так как оно не дает преподавателю лениться и расслабляться.
Постоянный прогресс, самосовершенствование – главные приоритеты моей жизни.
Я смогу вас научить, так как имею многолетний опыт работы со студентами разных возрастных групп, в разных форматах (онлайн, оффлайн). Каждый студент требует индивидуального подхода и поиска новых способов преодоления возникающих сложностей. Многочисленные приемы и методы работы, реализуемые на занятиях в течение почти 10 лет подкрепляются достижениями исследователей и ученых разных сфер – от психоанализа до лингвистики.
У меня высшее педагогическое образование по специальности преподаватель иностранного языка.
Я проходила курсы повышения квалификации (ментальная арифметика, скорочтение, информационно-коммуникационные технологии в дистанционном обучении).
Мой стаж преподавательской деятельности – 9 лет (английский язык), в ментальной арифметике – 8 лет, в скорочтении – 2 года.
Вы можете познакомиться с моими публикациями и книгами:
https://ridero.ru/books/mentalnaya_arifmetika_uroven_prosto/
https://ridero.ru/books/mental_maths/
https://ridero.ru/books/ege_i_oge_angliiskii_yazyk_na_5_slovoobrazovanie/
https://ridero.ru/books/angliiskii_yazyk_4/
https://ridero.ru/books/vpr_i_oge_angliiskii_yazyk_na_5/
Здравствуйте, меня зовут Яна Александровна.
Я преподаватель ментальной арифметики с 2012 года, автор методических пособий, сборников примеров по ментальной арифметике, авторских методик по совершенствованию навыков счета на абакусе и ментально.
В 2018 году был создан курс «Четыре вилки, три ножа и ложка». Его цель – с помощью ментальной арифметики, скорочтения и иностранных языков развивать внимание, память, координацию движений и мышление студентов.
В 2019 году создан видеоку…
Ментальная арифметика для детей начальных классов
Ментальная арифметика – специальная программа для развития интеллектуальных способностей детей младшего школьного возраста (скорость мышления, фотографическая память, зрительная зоркость, логическое мышление, периферическое зрение), основанная на системе устного счета. Мозг, который быстро работает и обрабатывает большое количество информации (сложение и вычитание многозначных чисел), решает сложные учебные задачи сегодня необходим школьнику, как одна из форм подготовки к экзаменам.
Согласно данным ученых, в младшем школьном возрасте происходит наиболее интенсивное развитие головного мозга, именно в этом возрасте необходимо больше внимания уделять на развитие умственных способностей ребенка. В этот период у детей наблюдается так называемая высокая пластичность мозга, что способствует росту клеток мозга и образованию между ними нейронных связей. Ведь, именно то, что сейчас вложит родитель, с этим багажом ребенок дальше идет в школьную, а затем во взрослую жизнь
Особенности обучения в нашем центре:
1. Полный комплект интересных и занимательных заданий и упражнений
2. В группе до 8 человек, поэтому достаточно внимания уделяется каждому ребенку, индивидуальный подход в приоритете.
3. Ребенок на каждом уроке учится выступать и отвечать перед другими детьми, становится более уверенным в себе, как следствие любит учиться.
4. Преподаватели высшей квалификационной категории, опытные педагоги и психологи, кандидаты наук
Основной результат:
Фундаментальные навыки: высокая скорость мышления, большой объем памяти, высокая концентрация внимания,
Учебные навыки: знает и пишет однозначные и двузначные числа, решает примеры на счетах и в уме однозначные и двузначные
Юные оскольчанки достойно представили наш город на турнире по ментальной арифметике
Устно решить длинный пример с трехзначными числами не всегда под силу даже преподавателям математики. А вот оскольчанки Влада Коновалова и Даша Плотникова в свои десять лет считают в уме не хуже, чем на калькуляторе. Девочки успешно осваивают ментальную арифметику.
Десятилетние Влада Коновалова и Даша Плотникова — очень занятые: ходят на теннис, учатся игре на фортепиано, увлекаются английским. Словом, талантливы во всем. Год назад занялись изучением ментальной арифметики. Теперь юные оскольчанки вычисляют многозначные примеры устно и в считанные секунды.
Я умею складывать, вычитать, умножать однозначные, двухзначные, трехзначные, четырехзначные числа. Мне в школе это помогает. На контрольных работах я могу считать по-разному: или ментально, или как учили. Когда мы считаем ментально, мы в голове у себя представляем абакус и пальцами считаем: складываем, вычитаем, умножаем числа.
— Владислава Коновалова и Дарья Плотникова.
Абакус — это счеты. Их придумали в Китае еще пять тысячелетий назад. Ментальная арифметика — это система развития детского интеллекта. Она построена на обучении быстрому счету в уме по древней методике. Родители отмечают, что такое развитие идет детям на пользу.
Стали меньше затрачивать времени на уроки. Ребенок, быстрее она стала запоминать все. Логическое стало развиваться лучше, то есть восприятие информации. Да, и как бы вот это бонус приятный, когда ребенок может посчитать быстро. Это не математика, это развитие интеллекта ребенка, то есть активация одновременной работы двух полушарий мозга. Классическая система обучения, она поочередность включает работы нашего мозга. А здесь как бы получается, что сразу вкупе все работает.
— Мария Коновалова, мама Влады.
Даша и Влада стараются подкреплять свои умения и на соревнованиях. Недавно они вернулись из Санкт-Петербурга, где проходил открытый турнир по ментальной арифметике «Кубок Пифагорки». 183 участника от 5 до 16 лет соревновались в счете. Из Центрального Черноземья были только две оскольчанки.
В возрастной категории «10–11 лет» участвовало более 40 участников. Первый этап у них проходил флэш-счет, где цифры менялись каждую секунду. Во втором этапе они считали на абакусе. 180 примеров надо было посчитать за 25 минут. И третий этап проходил: счет ментально. Так же 180 примеров в их категории было, но за 15 минут надо было их посчитать. Наши детки показали большие результаты.
— Анжела Плотникова, мама Дарьи.
По итогу девочки достойно представили наш город: из ста баллов Даша набрала 94,4, а Влада — 90. Сейчас юные счетоводы готовятся к очередному конкурсу. Он пройдет в Воронеже в марте 2019-го года.
Программа «Считалочка»
1. Вводное занятие «Будем знакомы, будем дружить!» (2)
2 2. Вводное занятие. Знакомство со счетами «Абакус». (2)
2 3. 1. Путешествие в страну «Циферию». (2)
1.1.Знакомство с цифрой «1». Учимся откладывать «1» на Абакусе.(2)
4. 1.2.Знакомство с цифрой «2». Учимся откладывать «2» на Абакусе. (2)
5. Введение понятий «Сложение» и «вычитание». (2)
6. Знакомство с цифрой «3». Учимся откладывать «3» на Абакусе. (2)
7. Знакомство с цифрой «4». Учимся откладывать «4» на Абакусе. (2)
8. Прямое сложение на нижних косточках. (2)
9. Прямое вычитание на нижних косточках.( 2)
10. Игра «Воображариум». Отработка навыка прямого сложения и вычитания на нижних косточках на счетах Абакус и на «воображаемых счетах». (2)
11. Занятие-приключение. Путешествие в Космос. Спасение планеты Ментарика (4)
12. 1.5. Знакомство с цифрой «5». Обучение откладыванию цифры «5» на счетах (2)
13. 1.6. Знакомство с цифрой «6». Обучение откладыванию цифры «6» на счетах (2)
14. 1.7.Знакомство с цифрой «7». Обучение откладыванию ее на Абакусе. Флеш-карты. Скоропись (2)
15. 1.8. Знакомство с цифрой «8». Обучение откладыванию ее на Абакусе. Флеш-карты (2)
16. 1.9.Знакомство с цифрой «9». Обучение откладыванию ее на Абакусе. Флеш-карты (2)
17. 1.10. А как же «0».??? Творческая математика. Учим счет играя. Обобщающее занятие о цифрах от «0» до «9» Решение задач на логику и внимание (4)
18. Прямое сложение. Отработка счета «±5» на счетах Абакус. Работа с флеш-картами. Воображаемые счеты (4)
19. Прямое сложение и вычитание. Отработка счета «±6,7» на счетах Абакус. Работа с флеш-картами. Воображаемые счеты (4)
20. Прямое сложение и вычитание. Отработка счета «±8,9» на счетах Абакус. Работа с флеш-картами. Воображаемые счеты. (6)
21. Отработка техники счета в «9ке» на Абакусе, прямое сложение и вычитание. Воображаемые счеты (4)
22. Выполнение сложения и вычитания на Воображаемых счетах в «9ке» (4)
23. Проведение викторины «Умникум» на умение откладывать на счетах Абакус, Воображаемых счетов, цифр в «9ке», умение совершать с ними математические действия (прямое сложение, вычитание) (4)
24. «Матемагия» решение математических задач. Магические квадраты, судоку и др. в пределах от «0» до «9» (2)
25. Развитие логического мышления с использованием счет Абакус. Решение текстовых задач арифметическим способом (4)
26. Выполнение сложения и вычитания на воображаемых счетах в «9ке». Диктант на счетах Абакус. Ментальный диктант (4)
27. Понятия «Число» и «Цифра» их сходства и отличия 4 28. Ведение понятий «однозначные» и «двузначные» числа. Откладываем «10ку» на Абакусе (4)
29. Развитие внимания с использованием флеш-карт От «0» до «10». Игры на развитие памяти и внимания (2)
30. Изучение понятий сложение и вычитание двузначных чисел на счетах Абакус на примерах от «10» до «19» (4)
31. Сложение и вычитание двузначных чисел на воображаемых счетах от «10» до «19» отработка навыка (4)
32. Изучение понятий сложение и вычитание двузначных чисел на счетах Абакус на примерах от «20» до «29» (4)
33. Отработка сложения и вычитания двузначных чисел от «20» до «29» на счетах Абакус и на воображаемых счетах( 4)
34. Изучение понятий сложение и вычитание двузначных чисел на счетах Абакус на примерах от «10» до «99» (14)
35. Работа с флеш-картами двузначные числа. Повторение сложения и вычитания двузначных чисел на счетах Абакус и на воображаемых счетах (от «10» до «99») (4)
36. Игра-квест «Легенда старинного замка» обобщающее занятие (4)
37. Повторение понятия «двузначные числа». Сложение и вычитание двузначных чисел на на счетах Абакус и на воображаемых счетах (6)
38. Изучение понятия о «трехзначных» числах. 2 39. Изучение понятия сложение и вычитание трехзначных чисел на счетах Абакус (4)
40. Сложение и вычитание трехзначных чисел на воображаемых счетах (6)
41. Итоговое занятие «Я умею считать на Абакусе» 2 42. Участие в групповом общеучрежденческом проекте «
Радость моя» (10)
Ментальная арифметика
Предметные результаты
Учащиеся получат возможность знать:
– о пользе обучения ментальной арифметике;
– правила работы на инструменте «абакусе»;
— правила сложения и вычитания однозначных чисел на абакусе;
— правила набора однозначных чисел на абакусе;
– правила техники безопасности при работе в классе.
Учащиеся получат возможность уметь:
— эффективно обрабатывать получаемую головным мозгом разносторонней информации;
— усовершенствовать навыки устного счета и логического мышления;
— четко и быстро решать поставленные разнообразные задачи;
– считать на соробане;
– считать ментально;
– использовать полученные знания в личностном развитии.
Личностные результаты:
— осознание себя членом общества, чувство любви к родной стране,
выражающееся в интересе к ее природе, культуре, истории и желании участвовать в ее делах и событиях;
— осознание и принятие базовых общечеловеческих ценностей,
сформированность нравственных представлений и этических чувств; культура поведения и взаимоотношений в окружающем мире;
– установка на безопасный здоровый образ жизни;
Метапредметными результаты:
— способность регулировать собственную деятельность, направленную на
познание окружающей действительности и внутреннего мира человека;
— способность осуществлять информационный поиск для выполнения
учебных задач;
— способность работать с моделями изучаемых объектов и явлений
окружающего мира.
— умение обобщать, отбирать необходимую информацию, видеть общее в единичном явлении, самостоятельно находить решение возникающих проблем, отражать наиболее общие существенные связи и отношения явлений действительности: пространство и время, количество и качество, причина и следствие, логическое и вариативное мышление;
— владение базовым понятийным аппаратом, необходимым для дальнейшего образования в области естественно-научных и социальных дисциплин;
— умение наблюдать, исследовать явления окружающего мира, выделять характерные особенности природных объектов, описывать и характеризовать факты и события культуры, истории общества;
— умение вести диалог, рассуждать и доказывать, аргументировать свои высказывания, строить простейшие умозаключения.
В программе используются такие формы занятий, которые мотивируют учащихся к активному слушанию, познанию изучаемого материала, а также обеспечивают наибольшую эффективность и оптимальность его восприятия, а именно: учебное занятие, практическое занятие, упражнения на развитие межполушарного взаимодействия, игры с флэш-картами.
Мысленно сложите двузначное и однозначное число
Это полный урок математики для 2-го класса, где дети учатся складывать в уме двузначное число и однозначное число, не переходя к следующим десяти, например, 35 + 4 или 61 + 5. Они складывают «внутри» та же десятка. Урок содержит и инструкции, и множество упражнений, и даже «бонусную» задачу-головоломку в конце.
Сначала добавьте 5 + 3. | Сначала добавьте 2 + 7. | Сначала добавьте 4 + 4. |
1. Написать дополнительное предложение для каждой картинки.
_______ + _______ = ______ | _______ + _______ = ______ |
_______ + _______ = ______ | _______ + _______ = ______ |
2.Добавлять. Сравните проблемы. Верхняя проблема помогает решить нижнюю!
а. 5 + 2 = _____ 35 + 2 = _____ | г. 4 + 5 = _____ 64 + 5 = _____ | г. 3 + 6 = _____ 93 + 6 = _____ |
3.Добавлять. По каждой проблеме подумайте о проблеме «помощи» с номерами меньше 10.
а. 52 + 7 = _____ 2 + 7 = _____ | б . 33 + 1 = _____ ____ + ____ = _____ | г. 11 + 5 = _____ _____ + ____ = _____ |
4.Цифры написаны в квадратах! Добавьте их в отдельный столбец.
Скопируйте число десятков внизу.
а. 35 + 3
| б. 12 + 6
| c. 57 + 1
| d. 64 + 3
|
5.Теперь вы, , пишете числа в квадратах. Добавьте их в отдельный столбец.
а. 26 + 3
| г. 72 + 4
| г. 65 + 4
| г. 81 + 4
|
6.Добавлять. Сравните проблемы.
| а. 6 + 2 = ______ 16 + 2 = ______ 36 + 2 = ______ | г. 4 + 3 = ______ 24 + 3 = ______ 34 + 3 = ______ | г. 5 + 4 = ______ 45 + 4 = ______ 65 + 4 = ______ | г. 11 + 7 = ______ 61 + 7 = ______ 41 + 7 = ______ |
7. Добавить много цифр.
| а. 20 + 5 + 2 = ______ 44 + 2 + 2 = ______ | г. 93 + 1 + 5 = ______ 83 + 4 + 3 = ______ | г. 100 + 5 + 4 = ______ 52 + 4 + 2 = ______ |
| Помните, как сломать число в его ДЕСЯТКИ И ЕДИНИЦЫ? |
|
|
8.Разбейте числа на десятки и единицы или сделайте наоборот.
а. 18 = 10 + 8 25 = _____ + _____ 55 = _____ + _____ | б. 32 = _____ + _____ 95 = _____ + _____ ______ = 40 + 9 | г. _______ = 60 + 6 _______ = 9 + 80 _______ = 8 + 70 |
9. Сравните. Писать <, > или =.
— это число, которого мы не знаем — загадочное число! Ваша задача |
Этот урок взят из книги Марии Миллер Math Mammoth Add & Subtract 2B и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер. На уроке рассматриваются следующие стандарты Common Core для 2-го класса: 2.OA.1 и 2.NBT.5.
Уловки и советы умственного умножения, чтобы быстрее выполнять умственную математику в голове
Приемы умножения и советы в этом посте позволят вам выполнять вычисления в уме быстрее, чем калькулятор, находящийся в вашей голове.Существует множество умственных стратегий умножения, но описанные здесь стратегии умственного умножения могут применяться для умножения любого набора чисел. Изучение советов по умножению умственных способностей из этого поста будет похоже на обучение катанию на велосипеде. Как только вы выучите это, действительно очень трудно это забыть.
Прежде чем мы продолжим, вы, должно быть, освоили однозначное умножение. Обязательным условием является знание ваших таблиц однозначного умножения от 1 x 1 до 9 x 9, прежде чем вы начнете умножать большие числа в уме.Если вы немного подзабыли, добавьте этот пост в закладки и сначала убедитесь, что вы запомнили свои однозначные таблицы умножения. Если вы хорошо умеете умножать однозначные числа, можете читать дальше.
Этот пост является второй частью серии «Уловки с умственной математикой». Настоятельно рекомендуется прочитать первый пост из этой серии — Уловки мысленной математики для скоростной математики, прежде чем приступить к изучению того, как выполнять мысленную математику при умножении.
Секрет умножения умножения
В первой части «Уловок ментальной математики» мы узнали, что математику в уме становится труднее выполнять, если вы считаете справа налево.Следовательно, секрет ментальной математики в том, чтобы делать противоположное и вместо этого вычислять слева направо. Решая слева направо, вы начнете называть ответ до того, как закончите полный расчет. Вычисление слева направо сначала может показаться немного странным, но после небольшой практики это станет естественным. В этом посте мы увидим, как применить это к умственному умножению.
Что такое множимое и множитель?
Прежде чем мы перейдем к уловкам умножения для выполнения мысленных вычислений, давайте быстро определим, что такое множимое и множитель.Возьмем, к примеру, задачу умножения 43 x 23. Здесь число 43 — это множимое — число, которое умножается. Число 23 — это множитель — число, на которое умножается первое число.
В этом посте есть несколько приемов умножения для умственной математики. У каждого метода умственного умножения будет два примера. Первый пример, видимый всем, познакомит вас с уловкой умножения. Во втором примере, видимом только для вошедших в систему пользователей, будут варианты, не описанные в первом примере.Так что войдите в систему или зарегистрируйтесь бесплатно, чтобы получить доступ ко всему контенту.
Уловки умножения для однозначного числа
Общее умножение для однозначного умножителя
Общий мысленный метод умножения — умножение слева направо. Хотя общий метод может применяться для любого числа, он работает лучше всего, когда числа не заканчиваются на 7, 8 и 9. У нас есть отдельный метод для чисел, заканчивающихся на 7, 8 и 9. А пока давайте применим умножение умножения умножить 5321 х 4.
Правило простое. Умножайте слева направо. По одной цифре за раз.
Умножение слева направо выполняется быстрее, потому что вам нужно запомнить меньше чисел, чтобы вызвать их и использовать позже. Вы сразу же начнете называть ответ с самого первого шага расчета.
Теперь попробуйте умножить 7142 x 6. Процедура такая же, как и раньше, и вы можете найти ее ниже:
Умножение в уме с округлением в большую сторону для однозначного множителя
Использование уловок умножения в уме после округления полезно, когда числа заканчиваются на 7, 8 или 9.Это значительно упрощает умножение. Давайте посмотрим, как применить это на примере. Умножить 68 x 3.
1. Округлите число
2. Умножить слева направо
3. Умножьте округленную сумму в большую сторону.
4. Вычтите числа из двух предыдущих шагов
Если вы попытаетесь сделать это так, как вы обычно делаете это на бумаге, вы поймете, что на то, чтобы сделать это в уме, уходит больше времени, чем то, что вам нужно сейчас. Если у вас еще нет скорости, не волнуйтесь.Это придет с практикой. В конце есть практические упражнения и рабочие листы умножения, которые вы можете скачать и практиковать.
Теперь вы попробуйте умножить 96 x 7. Процедура такая же, как и раньше, и вы можете найти ее ниже:
Умножение 2-значных чисел в уме
Общие уловки умножения
Давайте теперь посмотрим, как умножать в уме двузначные числа. Уловки умножения, которые мы видели ранее, нужно немного изменить.Давайте посмотрим, как это сделать, на примере. Умножить 36 x 32.
1. Разбить множимое
2. Умножить слева направо
3. Сложите отдельные ответы, чтобы получить окончательный ответ
Вы можете решить ту же задачу, разбив множитель вместо множимого. Ваш выбор будет зависеть от того, что дает вам более простой процесс сложения на шаге 3. Постарайтесь выбрать число, которое имеет меньшую цифру, потому что в большинстве случаев это обычно приводит к добавлению меньших чисел.
Теперь вы попробуйте умножить 26 x 23. Процедура такая же, как и раньше, и вы можете найти ее ниже:
Округление в большую сторону для двухзначного множителя
Как и в случае однозначных множителей, округление и умножение полезно, когда числа заканчиваются на 7, 8 или 9. Давайте посмотрим, как это сделать, на примере. Умножить 87 x 99:
1. Округлить число
2. Умножьте округленное значение на сумму, округленную в большую сторону слева направо.
3. Вычтите два числа
Теперь попробуйте умножить 41 x 57.Процедура такая же, как и раньше, и вы можете найти ее ниже:
Умножение умножения с использованием множителей
Как и округление в большую сторону, одна из уловок умножения состоит в том, чтобы разложить число на множители перед его умножением. Давайте посмотрим, как это сделать, попытавшись умножить 45 x 22.
1. Разложите на множители
.2. Умножьте число на первый множитель (слева направо)
4. Умножьте произведение на второй множитель (слева направо)
В уловках умножения, которые мы видели ранее, вам нужно будет запомнить произведение первой цифры, чтобы добавить / вычесть произведение второй цифры.Однако при умножении с использованием множителей вы просто умножаете второй множитель на первое произведение, так что вам не нужно запоминать столько чисел при вычислении.
Теперь вы попробуете умножить 21 x 63 с помощью факторного метода. Процедура такая же, как и раньше, и вы можете найти ее ниже:
Рабочие листы для практики умения умножения
Ниже вы можете скачать рабочие листы в формате PDF, чтобы применить описанные приемы умножения.
Калькулятор как человек
Вы узнали основные приемы умножения. Но Мы лишь поцарапали поверхность, и нам предстоит еще многое рассказать. Если вы действительно хотите стать человеком-калькулятором и вывести свои математические навыки на новый уровень, то посмотрите это видео. В видео я поделюсь историей о том, как я на самом деле боролся с математикой и как я стал тем, кем я являюсь сегодня. Вы узнаете секрет, который сократит вашу кривую обучения и ускорит ваш путь к математическому мастерству в уме.Чтобы посмотреть видео кликните здесь.
Заключение
Свои вопросы, пояснения и отзывы оставляйте в комментариях. Потребуется практика, прежде чем применение уловок умножения станет простым и легким. Поначалу вам будет сложно запомнить все числа в своей голове, когда вы будете считать. Но практика поможет вам улучшить кратковременную память на числа. Заставьте себя мысленно производить вычисления слева направо для повседневных вычислений и используйте калькулятор только для того, чтобы перепроверить свои числа.Чем больше вы практикуетесь, тем выше ваша скорость и способности.
быстрых арифметических советов: быстрое получение результата
При добавлении 5 к цифре больше 5 легче сначала вычесть 5, а затем прибавить 10.
Например,
7 + 5 = 12.
Также 7-5 = 2; 2 + 10 = 12.
При вычитании 5 из числа, заканчивающегося цифрой меньше 5, проще сначала добавить 5, а затем вычесть 10.
Например,
23-5 = 18.
Также 23 + 5 = 28; 28 — 10 = 18.
Точно так же часто удобнее сначала умножить на 2, а затем разделить на 10.
Например,
1375/5 = 2750/10 = 275.
Дополнительные примеры и пояснения
Часто удобнее вместо умножения на 5 сначала умножить на 10, а затем разделить на 2.
Например,
137 × 5 = 1370/2 = 685.
Дополнительные примеры и пояснения
Точно так же часто удобнее сначала умножить на 2, а затем разделить на 10.
Например,
1375/5 = 2750/10 = 275.
Дополнительные примеры и пояснения
Замените либо повторяющейся операцией на 2.
Например,
124/4 = 62/2 = 31.Также
124 × 4 = 248 × 2 = 496.
Вместо этого используйте операции с 4.
Например,
37 × 25 = 3700/4 = 1850/2 = 925.
Дополнительные примеры и пояснения
Замените либо повторяющейся операцией на 2.
Например,
124 × 8 = 248 × 4 = 496 × 2 = 992.
Вместо этого используйте операции с 8.
Например,
37 × 125 = 37000/8 = 18500/4 = 9250/2 = 4625.
Вы должны запомнить первые 25 квадратов:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 4 9 16 25 36 49 64 81 100 121 144 169 196 15 16 17 18 19 20 21 22 23 24 25 225 256 289 324 361 400 441 484 529 576 625 Если вы забыли запись .
Скажем, вам нужен квадрат 13. Сделайте следующее: прибавьте 3 (последняя цифра) к 13 (число, которое нужно возвести в квадрат), чтобы получить 16 = 13 + 3. Возведите последнюю цифру в квадрат: 3² = 9. Добавьте результат. на сумму: 169.В качестве другого примера найдите 14². Сначала, как и раньше, прибавьте последнюю цифру (4) к самому числу (14), чтобы получить 18 = 14 + 4. Затем, как и прежде, возведите последнюю цифру в квадрат: 4² = 16. Вы хотите добавить результат. (16) к сумме (18), получая 1816, что явно слишком велико, например, 14 <20, так что 14² <20² = 400.Вам нужно добавить 6 и перенести 1 к предыдущей цифре (8), получив 14² = 196.
Дополнительные примеры и пояснения
Квадраты чисел от 26 до 50 .
Пусть A будет таким числом. Вычтем 25 из A, чтобы получить x. Вычтем x из 25, чтобы получить, скажем, a. потом A² = a² + 100x. Например, если A = 26, то x = 1 и a = 24. Следовательно,26² = 24² + 100 = 676.
Дополнительные примеры и пояснения
Квадраты чисел от 51 до 99 .
Если A находится между 50 и 100, то A = 50 + x. Вычислите a = 50 — x. Тогда A² = a² + 200x. Например,
63² = 37² + 200 × 13 = 1369 + 2600 = 3969.
Дополнительные примеры и пояснения
Предположим, вы хотите найти 87². Найдите поблизости простое число — число, квадрат которого найти относительно легко. В случае 87 мы берем 90. Чтобы получить 90, нам нужно добавить 3 к 87; Итак, теперь давайте вычтем 3 из 87.Получаем 84. Наконец,
87² = 90 × 84 + 3² = 7200 + 360 + 9 = 7569.
Дополнительные примеры и пояснения
В случае, если A является преемником числа с известным квадратом, вы найдете A⊃, добавив к последнему самому последнему, а затем A. Например, A = 111 является преемником числа a = 110, квадрат которого равен 12100. Добавляем к этому 110 а затем 111, чтобы получить A²:
| 111² | = 110² + 110 + 111 |
| = 12100 + 221 | |
| = 12321. |
Дополнительные примеры и пояснения
Число, оканчивающееся на 5, имеет вид A = 10a + 5, где a на одну цифру меньше A. Чтобы найти квадрат A² числа A, добавьте 25 к произведению a × (a + 1) числа a с его преемником. Например, вычислите 115². 115 = 11 × 10 + 5, так что a = 11. Сначала вычислите 11 × (11 + 1) = 11 × 12 = 132 (так как 3 = 1 + 2). Затем добавьте 25 справа от 132, чтобы получить 13225!
Дополнительные примеры и пояснения
Аналогично возведению в квадрат чисел, оканчивающихся на 5:
Например, вычислите 113 × 117, где a = 11, b = 3 и c = 7. Сначала вычислите 11 × (11 + 1) = 11 × 12 = 132 (поскольку 3 = 1 + 2). Затем добавьте 21 (= 3 × 7) справа от 132, чтобы получить 13221!
Дополнительные примеры и пояснения
Это правило помогает запомнить большую часть таблицы умножения. Предположим, вы забыли товар 7 × 9.Сделай это. Сначала найдите превышение каждого из кратных над 5: это 2 для 7 (7-5 = 2) и 4 для 9 (9-5 = 4). Сложите их, чтобы получить 6 = 2 + 4. Теперь найдите дополнение этих двух чисел до 5: это 3 для 2 (5–2 = 3) и 1 для 4 (5–4 = 1). Помните их произведение 3 = 3 × 1. Наконец, объедините полученные таким образом два числа (6 и 3) как 63 = 6 × 10 + 3.
Дополнительные примеры и объяснение
Самый простой случай — когда два числа не слишком далеко друг от друга и их разница четная, например, пусть одно будет 24, а другое 28.Найдите их среднее значение: (24 + 28) / 2 = 26 и половина разницы (28–24) / 2 = 2. Вычтите квадраты:
28 × 24 = 26² — 2² = 676 — 4 = 672.
Древние вавилоняне использовали похожий подход. Они вычислили сумму и разницу двух чисел, вычли их квадраты и разделили результат на четыре. Например,
| 33 × 32 | = (65² — 1²) / 4 | |
| = (4225 — 1) / 4 | ||
| = 4224/4 | ||
| = 1056. |
Дополнительные примеры и пояснения
Скажем, вам нужно умножить 94 и 98. Возьмите их разности до 100: 100 — 94 = 6 и 100 — 98 = 2. Обратите внимание, что 94 — 2 = 98 — 6, так что для следующего шага не важно, какой из них вы используйте, но вам понадобится результат: 92. Это будут первые две цифры продукта. Последние два — всего 2 × 6 = 12. Следовательно, 94 × 98 = 9212.
Еще примеры и объяснения
Чтобы умножить двузначное число на 11, возьмите сумму его цифр. Если это однозначное число, просто напишите его между двумя цифрами. Если сумма 10 и более, не забудьте перенести 1.
Например, 34 × 11 = 374, поскольку 3 + 4 = 7,47 × 11 = 517, поскольку 4 + 7 = 11.
Вычитание часто выполняется быстрее в два шага вместо одного.
Например,
427 — 38 = (427 — 27) — (38 — 27) = 400 — 11 = 389.
Общий совет может быть таким: «Сначала удалите то, что легко, а потом, что останется».Другой пример:
1049 — 187 = 1000 — (187 — 49) = 900 — 38 = 862.
Добавление часто выполняется быстрее в два шага вместо одного.
Например,
487 + 38 = (487 + 13) + (38-13) = 500 + 25 = 525.
Общий совет может быть таким: «Сначала добавь то, что легко, а потом, что осталось». Другой пример:
1049 + 187 = 1100 + (187 — 51) = 1200 + 36 = 1236.
Часто быстрее добавлять цифру, начиная с более высоких цифр. Например,
| 583 + 645 | = 583 + 600 + 40 + 5 |
| = 1183 + 40 + 5 | |
| = 1223 + 5 | |
| = 1228. |
При умножении на 9 умножьте вместо этого на 10, а затем вычтите другое число.Например,
23 × 9 = 230 — 23 = 207.
Дополнительные примеры и пояснения
То же самое относится и к другим числам рядом с теми, для которых умножение упрощено:
| 23 × 51 | = 23 × 50 + 23 | |
| = 2300/2 + 23 | ||
| = 1150 + 23 | ||
| = 1173. | ||
| 87 × 48 | = 87 × 50 — 87 × 2 | |
| = 8700/2 — 160 — 14 | ||
| = 4350 — 160 — 14 | ||
| = 4190 — 14 | ||
| = 4176. |
Есть еще один способ быстрого умножения на 9, который имеет аналог умножения на 99, 999 и все подобные числа. Начнем с умножения на 9.
Чтобы умножить однозначное число a на 9, сначала вычтите 1 и получите b = a — 1. Затем вычтите b из 9: c = 9 — б . Затем просто напишите b и c рядом друг с другом:
9 a = b c .
Например, найдите 6 × 9 (так что a = 6.) Первое вычитание: 5 = 6 — 1. Вычтите второй раз: 4 = 9 — 5. Наконец, сформируйте произведение 6 × 9 = 54.
Аналогично для 2-значного a :
| b c | = 100 b + c |
| = 100 ( a — 1) + (99 — ( a — 1)) | |
| = 100 a — 100 + 100 — a | |
| = 99 a . |
Попробуйте такой же вывод для трехзначного числа. Например,
| 543 × 999 | = 1000 × 542 + (999 — 542) |
| = 542457. |
Дополнительные примеры и пояснения
Как быстро можно рассчитать сумму
97 + 86 + 83 + 95 + 85 + 70 + 84 + 72 + 77 + 81 + 70 + 85 + 84 + 76 + 92 + 66?
На этой странице показано, как это сделать быстро и без особых усилий.
Психологическое сложение детсадовцев с однозначными комбинациями в JSTOR
AbstractВ исследовании с участием 17 воспитанников были проверены основанные на ассоциациях и схемах представления о простом умственном сложении. Оказалось, что шестеро детей использовали механические правила: двое из них заявили одно из добавлений, добавили одно в дополнение и построили ответ подростка из одного из добавлений. Пятеро других детей, похоже, использовали более искренние методы оценки. Восемь недель вычислительной практики повлияли на ошибки непрактичных комбинаций при повторном тесте.Причем 7 из 10 детей освоили ранее неизвестные комбинации с участием нуля. Это было результатом изучения отношений (добавление нуля оставляет число неизменным), а не практики и запоминания отдельных фактов. Результаты показывают, что мысленно-арифметические ошибки, изменения в шаблонах ошибок и усвоение некоторых простых фактов не могут быть полностью объяснены практикой.
Информация о журналеОфициальный журнал Национального совета учителей математики (NCTM), JRME является ведущим исследовательским журналом в области математического образования и посвящен интересам учителей и исследователей на всех уровнях — от дошкольного до колледжа.
Информация об издателеНациональный совет учителей математики — это общественный голос в области математического образования, обеспечивающий видение, руководство и профессиональное развитие для поддержки учителей в обеспечении высочайшего качества обучения математике для всех учащихся. NCTM, насчитывающая около 90 000 членов и 250 аффилированных лиц, является крупнейшей в мире организацией, занимающейся улучшением математического образования в классах от дошкольного до 12-го класса. «Принципы и стандарты школьной математики» Совета являются руководящими принципами для достижения совершенства в математическом образовании и призывают всех учащихся. заниматься более сложной математикой.NCTM нацелен на постоянный диалог и конструктивное обсуждение со всеми заинтересованными сторонами того, что лучше всего для студентов нашей страны.
Ментальная математика — БУДЬТЕ ИЛИ B2: КВАДРАТ ДВУХЗНАЧНЫХ ЧИСЕЛ
Я рад представить новую функцию CompAct. Начиная с этого выпуска, мы будем включать отрывки из книги «Секреты ментальной математики: Руководство математика по вычислению молний и удивительных математических трюков» Артура Бенджамина и Майкла Шермера.Random House, Inc. любезно предоставила нам разрешение воспроизводить отрывки из этой книги каждый квартал в CompAct. Большая часть знаний, которые можно почерпнуть из этой книги, зависит от накопления определенных навыков в предыдущих главах; однако я постараюсь включить отдельные разделы. Приведенный ниже выбор включает упрощенный метод вычисления квадрата двузначного числа на основе некоторой базовой алгебры.
—Пол Рамирес, соредактор
Возведение чисел в квадрат (умножение числа на само) — одно из самых простых, но самых впечатляющих умений в уме, которые вы можете сделать.Я до сих пор помню, где был, когда узнал, как это делать. Мне было 13 лет, я ехал в автобусе навестить отца на работе в центре Кливленда. Я часто совершал это путешествие, поэтому мои мысли начали блуждать. Не знаю почему, но я начал думать о числах, которые в сумме дают 20, и мне стало интересно, насколько большим может быть произведение двух таких чисел?
Я начал с середины с 10 × 10 (или 10 2 ), произведение которого равно 100. Затем я умножил 9 × 11 = 99, 8 × 12 = 96, 7 × 13 = 91, 6 × 14. = 84, 5 × 15 = 75, 4 × 16 = 64 и т. Д.Я заметил, что продукты становились все меньше, и их разница от 100 составляла 1, 4, 9, 16, 25, 36,… — или 1 2 , 2 2 , 3 2 , 4 2 , 5 2 , 6 2 ,… (см. Таблицу ниже).
| Числа, которые добавляют к 20 | Расстояние от 10 | Их продукт | Отличия товара от 100 | |
|---|---|---|---|---|
| 10 | 10 | 0 | 100 | 0 |
| 9 | 11 | 1 | 99 | 1 |
| 8 | 12 | 2 | 96 | 4 |
| 7 | 13 | 3 | 91 | 9 |
| 6 | 14 | 4 | 84 | 16 |
| 5 | 15 | 5 | 75 | 25 |
| 4 | 16 | 6 | 64 | 36 |
| 3 | 17 | 7 | 51 | 49 |
| 2 | 18 | 8 | 36 | 64 |
| 1 | 19 | 9 | 19 | 81 |
Этот узор меня поразил.Затем я попробовал числа, которые складываются с 26, и получил аналогичные результаты. Сначала я вычислил 13 2 = 169, затем вычислил 12 × 14 = 168, 11 × 15 = 165, 10 × 16 = 160, 9 × 17 = 153 и так далее. Как и раньше, расстояния, на которые эти продукты находились от 169, составляли 1 2 , 2 2 , 3 2 , 4 2 и так далее (см. Таблицу ниже).
На самом деле существует простое алгебраическое объяснение этого явления (см. Почему эти уловки работают). В то время я недостаточно хорошо знал свою алгебру, чтобы доказать, что эта закономерность всегда будет иметь место, но я экспериментировал с достаточным количеством примеров, чтобы убедиться в этом.
Затем я понял, что этот шаблон может помочь мне легче возводить числа в квадрат. Предположим, я хочу возвести в квадрат число 13. Вместо умножения 13 × 13,
| Числа, которые добавляют к 26 | Расстояние от 13 | Их продукт | Отличия товара от 169 | |
|---|---|---|---|---|
| 13 | 13 | 0 | 169 | 0 |
| 12 | 14 | 1 | 168 | 1 |
| 11 | 15 | 2 | 165 | 4 |
| 10 | 16 | 3 | 160 | 9 |
| 9 | 17 | 4 | 153 | 16 |
| 8 | 18 | 5 | 144 | 25 |
Почему бы не получить приблизительный ответ, используя два числа, которые легче умножить, но при этом добавить к 26? Я выбрал 10 × 16 = 160.Чтобы получить окончательный ответ, я просто добавил 32 = 9 (поскольку 10 и 16 — это каждые 3 от 13). Таким образом, 132 = 160 + 9 = 169. Отлично!
Схема этого метода выглядит следующим образом:
Теперь посмотрим, как это работает для другого квадрата:
Чтобы возвести в квадрат 41, вычтите 1, чтобы получить 40, и прибавьте 1, чтобы получить 42. Затем умножьте 40 × 42. Не паникуйте! Это просто замаскированная задача умножения 2 на 1 (в частности, 4 × 42). Поскольку 4 × 42 = 168, 40 × 42 = 1680. Почти готово! Все, что вам нужно сложить, — это квадрат 1 (число, на которое вы пошли вверх и вниз от 41), что даст вам 1680 + 1 = 1681.
Можно ли возвести в квадрат двузначное число так просто? Да, с помощью этого метода и небольшой практики это возможно. И это работает независимо от того, округляете ли вы сначала вниз или вверх. Например, давайте рассмотрим 77 2 , вычислив его как округлением в большую, так и в меньшую сторону:
или
В этом случае преимущество округления в большую сторону состоит в том, что вы практически закончили, как только завершили задачу умножения, потому что к числу, оканчивающемуся на 0, просто прибавить 9!
На самом деле, для всех двузначных квадратов я всегда округляю в большую или меньшую сторону до ближайшего числа, кратного 10.Итак, если число, которое нужно возвести в квадрат, оканчивается на 6, 7, 8 или 9, округляйте в большую сторону, а если число, которое нужно возвести в квадрат, заканчивается на 1, 2, 3 или 4, округляйте в меньшую сторону. (Если число заканчивается на 5, вы делаете и то, и другое!) С помощью этой стратегии вы добавите только числа 1, 4, 9, 16 или 25 к вашему первому вычислению.
Давайте попробуем другую задачу. Вычислите 56 2 в уме, прежде чем смотреть, как мы это сделали, ниже:
Возвести в квадрат числа, оканчивающиеся на 5, еще проще. Поскольку вы всегда будете округлять в большую и меньшую сторону на 5, оба числа для умножения будут кратны 10.Следовательно, умножение и сложение особенно просты. Мы отработали 85 2 и 35 2 , ниже:
Как вы видели в главе 0, когда вы возводите в квадрат число, оканчивающееся на 5, округление вверх и вниз позволяет сразу же выпалить первую часть ответа, а затем закончить ее числом 25. Например, если вы хотите вычислить 75 2 , округляя до 80 и до 70, вы получите «Пятьдесят шестьсот… двадцать пять!»
Для чисел, оканчивающихся на 5, у вас не должно возникнуть проблем с тем, чтобы победить кого-нибудь с помощью калькулятора, а немного потренировавшись с другими квадратами, скоро вы сможете обыграть калькулятор с любым двузначным квадратным числом.Не стоит опасаться даже большого числа людей. Вы можете попросить кого-нибудь дать вам действительно большое двузначное число, что-то около 90-х, и это будет звучать так, как будто вы выбрали невозможную задачу для вычисления. Но на самом деле это еще проще, потому что они позволяют округлить до 100.
Допустим, ваша аудитория дает вам 96 2 . Попробуйте сами, а потом проверьте, как мы это сделали.
Разве не все было просто? Вы должны были округлить в большую сторону от 4 до 100 и от 4 до 92, а затем умножить 100 × 92, чтобы получить 9200.На этом этапе вы можете сказать вслух: «Девяносто двести», а затем закончить словами «Шестнадцать» и наслаждаться аплодисментами!
Почему эти уловки работают
Этот раздел предназначен для учителей, студентов, любителей математики и всех, кому интересно, почему наши методы работают. Кому-то теория может показаться такой же интересной, как и ее применение. К счастью, вам не нужно понимать, почему работают наши методы, чтобы понимать, как их применять. У всех фокусов есть рациональное объяснение, и математические фокусы ничем не отличаются.Именно здесь математик раскрывает свои самые сокровенные секреты!
В этой главе, посвященной задачам умножения, закон распределения — это то, что позволяет нам разбивать задачи на их составные части. Распределительный закон гласит, что для любых чисел a, b и c:
(b + c) × a = (b × a) + (c × a)
То есть внешний термин a распределяется или применяется отдельно к каждому из внутренних терминов b и c. Например, в нашей первой мысленной задаче умножения 42 × 7 мы пришли к ответу, рассматривая 42 как 40 + 2, а затем распределив 7 следующим образом:
42 × 7 = (40 + 2) × 7 = (40 × 7) + (2 × 7) = 280 + 14 = 294
Вы можете задаться вопросом, почему вообще действует закон о распределении.Чтобы понять это интуитивно, представьте, что у вас есть 7 сумок, каждая из которых содержит 42 монеты, 40 из которых золотые и 2 серебряные. Сколько всего у вас монет? Есть два способа прийти к ответу. Во-первых, по самому определению умножения есть монеты 42 × 7. С другой стороны, есть золотые монеты 40 × 7 и серебряные монеты 2 × 7. Следовательно, всего у нас есть (40 × 7) + (2 × 7) монет. Ответив на наш вопрос двумя способами, мы получаем 42 × 7 = (40 × 7) + (2 × 7). Обратите внимание, что числа 7, 40 и 2 можно заменить любыми числами (a, b или c), и применима та же логика.Вот почему действует закон распределения!
Используя аналогичные рассуждения для золотых, серебряных и медных монет, мы можем получить:
(b + c + d) × a = (b × a) + (c × a) + (d × a)
Следовательно, чтобы решить задачу 326 × 7, мы разбиваем 326 на 300 + 20 + 6, а затем распределяем 7 следующим образом: 326 × 7 = (300 + 20 + 6) × 7 = (300 × 7) + (20 × 7) + (6 × 7), которые затем складываем, чтобы получить ответ. Что касается возведения в квадрат, следующая алгебра оправдывает мой метод. Для любых чисел A и d
A2 = (A + d) × (A — d) + d 2
Здесь A — возведенное в квадрат число; d может быть любым числом, но я выбрал расстояние от A до ближайшего числа, кратного 10.Следовательно, для 77 2 я установил d = 3, и наша формула говорит нам, что 772 = (77 + 3) × (77 — 3) + 32 = (80 × 74) + 9 = 5929. Следующее алгебраическое соотношение также работает, чтобы объяснить мой метод возведения в квадрат:
(z + d) 2 = z 2 + 2zd + d 2 = z (z + 2d) + d 2
Следовательно, в квадрате 41 мы устанавливаем z = 40 и d = 1, чтобы получить:
41 & sup2 = (40 + 1) 2 = 40 × (40 + 2) + 1 2 = 1681
Аналогично (z — d) 2 = z (z — 2d) + d 2
Чтобы найти 77 2 , когда z = 80 и d = 3,
77 & sup2 = (80-3) 2 = 80 × (80-6) + 3 2 = 80 × 74 + 9 = 5929
Мой ребенок в школе | Манитоба Образование
Двумерные формы
Двумерные (2-D) формы — это фигуры, такие как круги, квадраты и треугольники, имеющие две меры
(е.грамм. длина, ширина или высота)
Объекты 3-D
Трехмерные (3-D) объекты также называют твердыми объектами. Это такие объекты, как призмы, пирамиды, цилиндры и конусы высотой
Математический факт или факт или факт
Факт сложения — это сложение двух однозначных чисел.Факты сложения включают суммы до 9 + 9.
( например, 10 + 7 = 17)
Факт вычитания — это вычитание однозначного числа из 18 или меньше. Факты вычитания включают разницы до
18–9. (Например, 15–6 = 9)
Двойные числа — это факты сложения, когда два сложенных числа одинаковы. (например, 1 + 1, 7 + 7)
Фактом умножения является умножение двух однозначных чисел до 9 x 9.(например, 3 X 7 = 21, 9 X 8 = 71)
Факты по математике для 2 класса
Сложение и вычитание до 10; удваивается до 9 + 9, и соответствующие факты вычитания
Представляющие числа
Представление чисел — это когда изображения, рисунки, символы или реальные объекты используются для отображения или обозначения чисел.
Стратегия
Метод или система шагов, используемых для решения проблем.Вот несколько примеров стратегий: рисование картинки или графика, поиск закономерностей, использование процесса исключения, использование проб и ошибок, а также применение умственных математических и оценочных стратегий.
Equation
Математическое предложение, утверждающее, что два выражения равны. Уравнение содержит знак равенства (=).
(например, 3+ 4 = 7)
Алгебраическое выражение
Математическая фраза, записанная с использованием одной или нескольких переменных и констант.(например, 3y + 6)
двойные столбчатые диаграммы
Диаграмма, на которой используются пары столбцов для сравнения и отображения взаимосвязи между данными.
Вместимость
Общее количество жидкости (жидкости или газа) в контейнере, обычно измеряемое в метрической единице литр (л) или миллилитр (мл). Пример: емкость с молоком на 500 мл.
Стратегия
Метод или система шагов, используемых для решения проблем.Вот несколько примеров стратегий: рисование картинки или графика, поиск закономерностей, использование процесса исключения, использование проб и ошибок, а также применение умственных математических и оценочных стратегий.
Equation
Математическое предложение, утверждающее, что два выражения равны. Уравнение содержит знак равенства (=). (например, 3+ 4 = 7)
Выражение
Математическое представление, содержащее числа, переменные и / или символы операций; выражение не включает символ отношения (<,>, =, ≠).Примеры: (5 + 2) — 27 ÷ 3 (арифметическое / числовое выражение) 2a + 3b (алгебраическое / символьное выражение)
Факторы
Число или выражение, которое умножается на другое для получения продукта (например, коэффициент 24 равен 8, потому что 8 × 3 = 24, а коэффициент 3n равен n, потому что 3 × n = 3n).
Mental math
Математика, выполненная «в уме», полностью или частично.
Кратное
Произведение заданного целого числа на любое другое целое число.(например, 18 делится на 6, так как 6 × 3 = 18)
мм, см и м
Метрические единицы измерения длины — миллиметр (мм), сантиметр (см) и метр (м)
Переменная
Символ, используемый для представления числа в выражении или неизвестного значения в уравнении. (например, 2 n + 3 [переменная n ], a + 3 = 5 [переменная a ])
Объем
Объем трехмерного пространства, заключенного в замкнутую границу, часто измеряемый в кубических метрах (м3) или кубических сантиметрах (см 3 ).Пример: объем кубика сахара составляет примерно 3,4 см 3 .
Порядок операций
Заданная последовательность, в которой должны выполняться математические операции, такие как сложение, вычитание, умножение и деление.
Тесселяция
Создайте узор, соединяя формы вместе в повторяющийся узор без промежутков или перекрытий.
Линейные графики
График, на котором сегменты линий используются для отображения изменений данных; данные обычно представляют тенденции, отношения или количество, изменяющееся с течением времени.
Сегменты линии
Прямая линия, соединяющая две точки, но не выходящая за их пределы.
Целые числа
Набор чисел, состоящий из целых чисел (например, 1, 2, 3, 4,…), их противоположностей (например, -1, -2, -3, -4,…) и 0
Слайды или перемещение
В геометрии — преобразование, при котором объект перемещается по прямой линии без поворота или изменения размера или формы.Каждая точка объекта перемещается на одинаковое расстояние и в одном направлении.
Оборотов
В геометрии преобразование, при котором объект перемещается относительно фиксированной точки, называется точкой вращения.
Отражения или переворот
Преобразование в геометрии, при котором объект отражается по прямой линии, образуя зеркальное отображение.Каждая точка объекта и соответствующая точка на изображении находятся на одинаковом расстоянии от линии отражения.
Параллелограммы
Четырехсторонняя форма с двумя парами параллельных сторон.
Среднее значение
Среднее арифметическое чисел. Мера центральной тенденции. Частное, полученное при делении суммы чисел в наборе на количество слагаемых.
Медиана
Среднее значение в упорядоченном списке. Если среднего значения нет, медиана — это среднее из двух средних значений. Примеры: Медиана чисел 1, 1, 2, 4, 5, 6 и 7 равна 4. Медиана чисел 1, 1, 2, 4, 5, 6, 7 и 7 равна 4,5.
Режим
Число или элементы набора данных, которые наиболее часто встречаются в наборе данных.Примеры: В наборе 87, 85, 86, 90 и 86 режим равен 86. В наборе 87, 85, 86 и 90 режима нет.
Диапазон (набора данных)
Разница между наибольшим и наименьшим значениями в наборе чисел. Примеры: Для данных: 2, 7, -3, 14, -1, 6, 34, 3 Диапазон: 34 — (-3) = 37
Количество навыков
Умение решать математические задачи, используя знания числовых моделей и математических стратегий в уме.
Числовой смысл
Хорошее концептуальное понимание чисел и их концепций.
Площадь
Мера внутренней поверхности замкнутой области или фигуры; Площадь измеряется в квадратных единицах, например м 2 или см 2 .
Теорема Пифагора
Математическое соотношение, утверждающее, что в любом прямоугольном треугольнике сумма квадратов двух катетов равна квадрату гипотенузы; если a и b — длины катетов, а c — длина гипотенузы, то a2 + b2 = c2.
Квадратный корень
Число (коэффициент), которое при умножении на себя дает данный квадрат. (например, квадратный корень из 16 равен 4)
Линейные уравнения
Уравнение, которое можно представить графически прямой линией. (например, y = 2x — 7)
Свидетельства об обучении
Свидетельство обучения — это демонстрация того, что студент узнал.
Масса
Вес показывает, сколько стоит оценка в процентах от общей оценки.
Однозначное сложение — от простого к сложному.
Вернуться к страницам по естествознанию и математике Дональд Заутер.
Однозначное сложение —
Не все проблемы сложения одинаковы!
и nbsp
*** Введение ***(Первые несколько параграфов введения здесь такие же, как и в сопутствующая страница однозначное умножение.)
Если вы никогда не замечали, почти все, что вы делаете по математике, просто некоторая смесь сложения и умножения (признавая, что вычитание связано со сложением, а деление с умножением.) все сложение и умножение, какими бы большими или сложными они ни были, выполняется пошагово в мозгу по две цифры за раз, вы увидите, что ценность быстрых и надежных ответов на однозначные дополнения и умножения невозможно переоценить.
Просто нет смысла в идти дальше в математике без полного владения однозначными числами сложение и умножение.
а в чем проблема? Разве это не детские вещи? Не все научиться сложению в первом классе и умножению в третьем классе?
Не далеко. У меня было много возможностей наблюдать за математикой навыки многих людей, от начальной школы до средней школы и колледжа умным, образованным взрослым, и то, что я вижу, находится где-то посередине душераздирающий и ужасающий.
У меня есть определенные представления о том, что в школах делают неправильно математика. Для начала калькуляторы. Теперь я не могу поклясться, что ни один студент никогда не выучил немного математики , несмотря на калькуляторов, но уверяю вы нет студент, где бы то ни было, когда-либо изучал математику с Калькулятор. Грррр … И есть безумная одержимость письменными объяснениями из «как вы получили свой ответ». Студенты движутся по конвейеру ремень независимо от того, насколько мало прилипло.И, извините за это, основное Математику преподают учителя, которые сами никогда не учили базовой математике. Безумие продолжается уже несколько поколений.
Но мы здесь, чтобы приступить к сложению и найдите способ поразмыслить над каждым основным фактом. Очевидно, что первый сам оценщик не будет это читать, поэтому целевая аудитория любой, кто работает со студентами в этой важной области, или любой желающий восполнить пробелы в собственных базовых математических навыках на любом этапе жизни.
Мы стремимся к «быстрым ответам» на все однозначные дополнения. Было бы здорово, если бы мы могли просто запомнить их, но, если быть реалистом, это непростая задача даже для «действительно умного» человека. Но «быстрый» практически не уступает «мгновенно», и если требуется быстрый промежуточный мысленный шаг или два, это вполне приемлемо. Но не надо возиться. Подсчет НЕ допускается.Это слишком медленно и рискованно; всегда есть лучший способ думать об этом.
Само собой разумеется, использование пальцев НЕ допускается. В математике нет завтрашнего дня, если ты не можешь выйти за рамки пальцев.
Вот таблица сложения:
+0 +1 +2 +3 +4 +5 +6 +7 +8 +9
-----------------------------
0 | 0 1 2 3 4 5 6 7 8 9
1 | 1 2 3 4 5 6 7 8 9 10
2 | 2 3 4 5 6 7 8 9 10 11
3 | 3 4 5 6 7 8 9 10 11 12
4 | 4 5 6 7 8 9 10 11 12 13
5 | 5 6 7 8 9 10 11 12 13 14
6 | 6 7 8 9 10 11 12 13 14 15
7 | 7 8 9 10 11 12 13 14 15 16
8 | 8 9 10 11 12 13 14 15 16 17
9 | 9 10 11 12 13 14 15 16 17 18
Некоторые учебные программы по математике проходят столбец за столбцом, начиная с «плюс 1». до «плюс 2», до «плюс 3» и так далее до «плюс 9».Это может показаться разумным поскольку добавить что-то большее должно быть сложнее, чем добавить что-то меньшее, правда? Но внимательно посмотрите на вращающиеся шестерни в вашем мозгу, пока вы добавляете, указывает, что мы можем добиться большего.
Итак, вот более естественный переход от самого простого к сложному для однозначные дополнения. По мере того, как мы шагаем вперед, я пытаюсь предложить способ обдумывая каждый из дополнительных фактов. Для большинства людей есть Только некоторые из них вызывают проблемы, так что не стесняйтесь сосредотачиваться на них.
и nbsp
*** Плюс 0 ***Ноль — это число «ничего не делать», когда вы выполняете сложение. Ноль — это ничто, а что-то плюс ничто — это то же самое.
Что может быть проще? Ничего, кроме того, что когда происходит умножение, 0 делает что-то каждый бит, как легко — но совершенно другое! В умножении это превращает все в 0. Когда придет время, не забудьте будьте в напряжении.Всегда давайте +0 и x0, какими бы тривиальными они ни были, вторая мысль.
(Однажды я посвящу этому веб-страницу, но подумайте о математике как разделенные на две «комнаты» — дополнительную и комната умножения. В каждой комнате есть свой набор инструментов, многие из которые соответствуют, но не идентичны инструментам в другая комната. Например, в каждой комнате есть номер «ничего не делать». «элемент идентичности». В дополнительной комнате это число 0; в комната умножения это 1.Вы всегда должны быть полностью знать, в какой комнате вы работаете, сложение или умножение. Какой бы сложной ни была математическая задача, ваш мозг всегда работает в одном помещении одновременно. В любой момент вы делаете или сложение или умножение, быстрый шаг туда и обратно между комнатами по мере необходимости. И, повторюсь, независимо от того, насколько сложным становится сложение или умножение, ваш мозг обрабатывает только пару одиночных цифр за раз.В двух словах: вся математика — это просто смесь однозначных чисел. сложение и однозначное умножение. )
Но вернемся к плюсам 0:
0 + 0 = 0
1 + 0 = 1
2 + 0 = 2
3 + 0 = 3
4 + 0 = 4
5 + 0 = 5
6 + 0 = 6
7 + 0 = 7
8 + 0 = 8
9 + 0 = 9
Конечно, мы не запоминаем эти десять фактов сложения; мы просто знаем, что добавление нуля ничего не дает.
и nbsp
*** Плюс 1 ***Это просто «следующий» номер. Вы слышали, как я разглагольствовал выше что никогда не должно быть необходимости в подсчете однозначных чисел добавление. Я имею в виду, что если факт сложения не запомнился, всегда есть способ быстрее, безопаснее и лучше, чем считать. Но я признает, что в этом случае нет большой разницы между мгновенной визуализацией следующего более высокого соседа в 0 через 9 цикл по сравнению с простым подсчетом одного.
1 + 1 = 2
2 + 1 = 3
3 + 1 = 4
4 + 1 = 5
5 + 1 = 6
6 + 1 = 7
7 + 1 = 8
8 + 1 = 9
9 + 1 = 10
Мы опускаем 0 + 1, потому что мы думаем об этом как о 1 + 0, что мы уже знаем из таблицы «плюс 0».
И это подводит к важному моменту. Чтобы сделать жизнь намного проще, и чтобы вдвое сократить количество основных фактов сложения, вы всегда «загружаете» два числа в одном и том же порядке в вашем мозгу, независимо от того, как они появляются на бумаге или в том порядке, в котором их слышат ваши уши.Ты почти всегда будешь загрузите их как больше плюс меньше. Обычно мы думаем о сложении как наваливать больше на основную сваю, верно? Если бы вы считали куча денег, вы бы начали с двадцатых, потом с десятков, потом пятерки и так далее до грошей; А не наоборот. Если вы добавите в стадо еще 3 бычков, вы, естественно, подумаете о это как «5491 плюс 3», а не как «3 плюс еще 5491».
Итак, когда вы видите или слышите «0 + 1», в вашем мозгу появляется «1 + 0», в этот момент срабатывает правило «плюс 0»: «ноль не меняется ничего! »Это лучше, чем считать один с нуля.Мы могли бы только в этом случае сэкономить миллионную долю секунды, но в целом всегда делать один и тот же фундаментальный математический факт одним и тем же способом имеет серьезные преимущества с точки зрения скорости, простоты и точности.
и nbsp
*** Плюс 2 ***Добавление 2 — это просто переход к следующему четному или нечетному.
Следующее в математике после обучения счету следует развивать мгновенное распознавание четного и нечетного.Я знаю, что школы пытаются это сделать, но не думаю, что они знают об этом. насколько это фундаментально и важно. Я встречаю много учеников старших классов которые признают, что не считают числа четными или нечетными. К нему следует вернуться так часто, как это необходимо в течение младшего школьного года, чтобы убедиться у каждого студента он есть в кровотоке. Это то, что не требует подумал, так же как не нужно думать, чтобы определить, встретишь ли ты кого-то мальчик или девочка; это мгновенно.
На самом деле, я всегда проводил аналогию равных против разногласий с полом; добрые добрые, хорошо воспитанные вечера номера девушек, а непослушные, нечетные нечетные числа — плохие парни. Не спрашивайте меня, сохраняется ли аналогия или мы позволено думать так больше.
Так что каждый должен уметь бездумно греметь «два, четыре, шесть, восемь «- с полным пониманием того, что на обоих концах есть 0, который считается как даже.Шансы — 1, 3, 5, 7, 9, но это не обязательно . чтобы запомнить последовательность. Когда «два, четыре, шесть, восемь (кто мы цените!) «тщательно прожарен, шансы просто» другие «, те, что в промежутках, те, что , даже не .
2 + 2 = 4
3 + 2 = 5
4 + 2 = 6
5 + 2 = 7
6 + 2 = 8
7 + 2 = 9
8 + 2 = 10
9 + 2 = 11
Я опускаю 0 + 2, потому что он попадает в наш мозг как 2 + 0 — «ничего не делать!»
Я опускаю 1 + 2, потому что оно попадает в наш мозг как 2 + 1 — «следующее число вверх!»
В остальном мы делаем один мгновенный шаг к следующему четному или как ни странно.Обратите внимание, что 8 + 2 может быть более естественным. как «пара, которая составляет 10», и 9 + 2 как «пара, которая составляет 11» (см. ниже). Но они оба настолько просты, что это просто расщепление волос.
Сделаем небольшую передышку. «Почему?» ты спрашиваешь. «Мы только начали, и мы сделали только детские вещи, которые все и так уже знают «. Верно, но вы можете быть удивлены, узнав, что то, что мы сделали, далеко — плюс 0, плюс 1 и плюс 2 — составляет больше половины однозначных сложений, то есть 51 из 100 задач в таблице сложения.Математика — это так просто!
и nbsp
*** 5 плюс небольшое число ***А вы подумали, что «плюс 3» последует за «плюсом 2». Тебе должно быть стыдно за то, что никогда не заглядываете внутрь себя, на шестеренки, крутящиеся в вашем мозгу! Это, безусловно, , а не — вообще говоря, легко мгновенно визуализируйте следующую цифру 3 вверх.
Я поставил «5 плюс небольшое число» в этот слот как следующий самый простой базовый добавление.Это связано с тем, как мы научились считать. Ты бы пошел пальцами одной руки, а когда они кончились, начинаем пальцами следующего от 6 до 10. Таким образом, маленький ребенок может поднимите одну руку из вытянутых пальцев плюс указательный палец другой стороны, чтобы указать 6, и так далее. Таким образом, «5 плюс небольшое количество «прожигается почти с самого начала.
ВАЖНОЕ ПРИМЕЧАНИЕ: Когда я говорю о руках и пальцах как о основы для размышлений о различных основных фактах, я НЕ предлагаю используя пальцы, чтобы сделать сложение.Это НИКОГДА не разрешено. Если это наблюдается, он ДОЛЖЕН быть удален. Если бы я был ответственным, кого бы поймали использование пальцев будет отправлено обратно во второй класс, и столько же раз по мере необходимости, чтобы избавиться от привычки. Погружение в математику вычисления пальцами — это все равно что учиться танцевать с башмаками из шлакоблоков.
Как и в случае с , все однозначных сложений, которые не превышают 10, эти должны быть мгновенными, без промежуточных шагов для перехода к ответ:
5 + 1 = 6
5 + 2 = 7
5 + 3 = 8
5 + 4 = 9
5 + 5 = 10
С общими «плюс 1» и «плюс 2» мы уже разобрались, но 5 — это такой хорошая отправная точка, с которой можно так же быстро распознать 5 + 1 и 5 + 2 и обрабатывается как часть этой группы.
Но 5 + 3 и 5 + 4 — важные новые. В твоей мысленным взором вы видите на одной руке пальцы плюс 3 или 4 на другой. Бинго.
Почему я не позвонил 5 + 5? Это более естественно обрабатывается в следующая категория.
и nbsp
*** Маленькие двойники ***Помните, что у нас в душе есть четное и нечетное? Ну а маленькие двойники, то есть двойники чисел, которые могут быть на одной руке (от 1 до 5) — это просто четные числа до 10.
1 + 1 = 2
2 + 2 = 4
3 + 3 = 6
4 + 4 = 8
5 + 5 = 10
Нам не нужен другой способ просмотра 1 + 1, который здесь можно было бы опустить.
Мы также можем опустить 2 + 2, так как мы сделали «плюс 2», но я считают, что более естественно рассматривать 2 + 2 как «две двойки», чем как увеличивая 2 или, как я предлагаю, даже переходя к следующему.
И подумайте, как естественно ребенку держать два пальца на каждой рукой указать 4; по три по 6 шт .; и четыре штуки по 8.Мы все держим на 10 пальцев целых две руки; есть Другого пути нет!
Другими словами, даже если эти проблемы представлены на бумаге как дополнительные проблемы, мозг действительно обрабатывает их как задачи умножения — очень простые задачи умножения, которые мы делали это еще до того, как услышали слово «умножение».
и nbsp
*** Пары, составляющие 10 ***И снова мы мельком мельком взглянем на свои пальцы.Есть 10 из их, что является настолько фундаментальным числом, что они основали всю нашу система счисления на нем! И очень рано вы должны были заметить это, если вы поднимете определенное количество пальцев, чтобы показать определенное число, и сосчитайте удерживаемые, эти два числа составляют 10. (Ой, вот и мы, даже не доделали базовые дополнения и мы касаемся вычитания.) Или, если вы не заметили, теперь пора гореть парами, которые дают «две пригоршни»:
1 + 9 = 10
2 + 8 = 10
3 + 7 = 10
4 + 6 = 10
5 + 5 = 10
6 + 4 = 10
7 + 3 = 10
8 + 2 = 10
9 + 1 = 10
Кто бы мог запомнить такую сложную неразбериху? Ну после мы отсеяли те, в которых уже сгорели, единственными новыми являются:
6 + 4 = 10
7 + 3 = 10
Как всегда, я рассчитываю, что вы автоматически сделаете мысленный триггер, если вам дают «4 + 6» или «3 + 7».Большой плюс маленький …
и nbsp
*** Пары, составляющие 11 ***Теперь, когда у нас есть пары, которые составляют 10 сгоревших, мы можем видеть в момент, когда пара просто переходит 10 на одну.
5 + 6 = 11 (сразу видно, как на единицу больше 5 + 5 = 10)
7 + 4 = 11 (сразу видно, как на единицу больше 7 + 3 = 10)
8 + 3 = 11 (сразу видно, как на единицу больше 8 + 2 = 10)
9 + 2 = 11 (сразу видно как на единицу больше, чем 9 + 1 = 10)
Мы встретили 9 + 2 в категории «плюс 2», но я думаю, что это немного здесь более естественно вписывается.
Также обратите внимание на представление «5 + 6», а не «6 + 5». Безусловно эту проблему гораздо легче увидеть как «две пятерки плюс еще одна», скорее чем «на один больше 6 + 4».
и nbsp
*** Большие двойники ***Это удвоение чисел, для которых требуется две руки, от 6 до 10. Они должны быть мгновенными, несмотря на то, что ответы двузначный. Как и в случае с маленькими двойниками, большие двойники фактически обрабатываются в нашем мозгу как умножения.Здесь ответы — все четные числа от 12 до 20 — и мы профессионалы в четные числа!
6 + 6 = 12
7 + 7 = 14
8 + 8 = 16
9 + 9 = 18
10 + 10 = 20
Таким образом, две шестерки сразу же считаются первым четным числом после 10; и две девятки должны быть наибольшим четным числом, прежде чем вы дойдете до 20. Забавно слышать студентов, у которых может быть несколько слабых мест оставаясь в своей таблице сложения, набросайте 9 + 9 = 18 без промедления. колебания.Больше не значит труднее!
Тогда 7 + 7 и 8 + 8 — оставшиеся два события. от 12 до 18 лет. Кем еще они могут быть, кроме 14 и 16 соответственно?
и nbsp
*** 9 плюс что угодно ***Девять — это самое большое и неуклюжее однозначное число. (Я не скажу самый причудливый или самый эксцентричный — это 7.) Но то, что 9 имеет для этого, так это что это прямо рядом с 10, а работать с 10 — чистое удовольствие.Предлагаемый мыслительный процесс для «9 плюс кое-что» — украсть один от «чего-то», что дает вам от 9 до 10, а затем то, что осталось от «чего-то» вас перескакивает к окончательному ответу.
Превращение этого в быстрый и легкий «рецепт»:
- Выпадайте один из другого номера.
- Поставьте цифру «1» впереди.
- Бинго!
9 + 3 : Спуститесь с 3 до 2 .Поставьте впереди « 1 «. Бинго, 12 !)
9 + 4 : Спуститесь от 4 до 3 . Поставьте впереди « 1 «. Бинго, 13 !)
9 + 5 : выпадайте из списка 5 до 4 . Поставьте спереди « 1 «. Бинго, 14 !)
9 + 6 : Спуститесь с 6 до 5 . Поставьте впереди « 1 «. Бинго, 15 !)
9 + 7 : Спуститесь с 7 до 6 .Поставьте впереди « 1 «. Бинго, 16 !)
9 + 8 : выпадайте из списка 8 до 7 . Поставьте впереди « 1 «. Бинго, 17 !)
Я исключил из списка 9 + 0, 9 + 1, 9 + 2 и 9 + 9, так как мы прибили их гораздо более простыми способами.
Если вы спросите меня, эти «9 с лишним» фактов никогда не нужно запоминать. Ты можешь получите ответы достаточно быстро, используя этот рецепт «9 с плюсом». Помните, что мы использовали добрые, старые 10 как ступенька раньше, в парах, составляющих 11.Думайте о 10 как о первой базе в бейсболе. Это делает приятный, безопасный, удобное место для того, чтобы добраться и отбыть во время поездки из одинарные цифры в двойные цифры. Мы встретим еще несколько примеров это в нашей последней, зачаточной категории ниже.
и nbsp
*** Остатки ***Вот однозначные сложения, не попадающие ни в одну из категории выше. Я разделил их на связанные пары, и я оставил беспорядок ответов, чтобы решить сами проблемы более заметны.
4 + 3
6 + 3
8 + 4
8 + 6
7 + 6 (или 6 + 7 лучше?)
8 + 7 (или 7 + 8 лучше?)
7 + 5 (или 5 + 7 лучше?)
8 + 5 (или 5 + 8 лучше?)
Спуск по списку. . .
4 + 3 : Как и все однозначные сложения, которые подходят для двух рук, этот должен быть немедленно доступен из банков памяти. я не знаю, что 4 + 3 вызывает проблемы, но если да, возможно, это поможет укажите, что это должно быть нечетное число (используйте фишки, чтобы показать, что число плюс его сосед должен быть странным), и что этот, очевидно, должен попадают между 5 и 10.Но мне кажется, что это перебор для 4 + 3. . .
6 + 3 : Опять же, у этого должно быть мгновенным. Я был поражен один раз услышать, как умный, образованный взрослый выполняет 6 + 3, быстро бормоча: «семь, восемь, девять ». Не считайте! Вы можете получить его мгновенно в последняя часть знакомой последовательности 3, 6, 9 «счет троек». Четный хотя это исходит из математики более высокого порядка (умножение), я предлагаю забегая вперед, чтобы поиграть со счетом троек, как способ забить 6 + 3 = 9.Рано или поздно студент должен прийти, чтобы увидеть этих троих, открытыми 3, 6 и 9 цифрами как милая, теплая, маленькая семья, которая абсолютно «капает с троек». С таким же успехом могло быть и раньше.
Другой подход может заключаться в том, чтобы указать, насколько ясно 6 + 3 не достаточно большой, чтобы достичь 10, что требует 6 плюс 4.
8 + 4 : Я не могу точно сказать, осуществляется ли доступ к нему из жесткой памяти в моем мозгу, или я почти сразу вижу ответ 12 как формирующий идеальная симметрия с восьмеркой вокруг хорошей, старой десятки.Проблема вопиет «ровность»; четверка практически распадается на две двойки, одна из которых приведет вас к 10, другой к 12 .
8 + 6 : Опять же, я не могу быть уверен, доступен ли это в одном мгновенный шаг по памяти. Это могло произойти из-за молниеносного процесса исключения. У нас есть два числа, которые настолько четны, насколько это возможно, образуя верхнюю половину «два, четыре, шесть, восемь!» Таким образом сумма должна быть четной.Ответ должен быть более 10, но не огромное количество, и это точно не 12, и уж точно не 16, так что еще это может быть, кроме 14 ? Весь мыслительный процесс доли миллисекунды. . .
7 + 6 и 8 + 7 : Эти два всегда были мгновенными для мне, без намека на промежуточные шаги. Но я встречал много студентов, которые наткнуться на них. Может быть, стоит упомянуть, как мы это сделали в отношении до 4 + 3, что число плюс его сосед должно быть нечетным.Тем не менее, это только ограничивает выбор; это не дает нам ответа.
Для 6 + 7 лучшее, что я могу предложить, это быстрое удвоение 6 до 12, и прибавляем 1, чтобы получить 13 . Сделав это несколько раз, надеюсь, 13 запишется в память.
Для 8 + 7 что-то подобное сделать можно, но думаю есть что-то лучше. Обратите внимание, что эти два числа находятся «посередине» 5 и 10. Все знают, что две пятерки — это 10, а две десятки — 20, так что это не должно быть. сюрприз, что 8 + 7 попадает прямо в середину 10 и 20, что 15 .Указание на это студенту может помочь ему сгореть. факт 8 + 7 = 15.
7 + 5 и 8 + 5 : Вот два убийцы в однозначном дополнения. Я не горжусь сказать, что большую часть своей математической жизни я использовал быстрая мысленная процедура (и, возможно, еще есть отголоски этого). Я бы взял меньшее число, 5, и разбейте его на две части. Поскольку 5 — нечетное число, мы это знаем. не ломается равномерно; он разбивается со смещением от центра на куски по 2 и 3.Один из этих фрагментов вы получите 10 хороших, старых, безопасных, а второй фрагмент переходит к окончательному ответу.
Итак, для 7 + 5, после разделения 5 на две части, 7 ( меньший из 7 и 8) требуется большой кусок (3), чтобы получить до 10; и 10 плюс оставшийся кусок (2) позволяет перейти к ответу (12). Аналогично, 8 ( большего размера из 7 и 8) требуется только маленький кусок (2), чтобы получить вам до 10 лет; и 10 плюс оставшийся кусок (3) переходят вас к ответ (13).
Вот как это разыгралось в моей голове, вероятно, из-за моей нерушимой привычка автоматически располагать слагаемые как «большие плюс маленькие» в мозг. Сделав исключение в этом случае и увидев проблемы как 5 + 7 и 5 + 8, возникает гораздо более элегантная процедура. Помнить наша категория «5 плюс немного»? Это был один из наших самых простых и в большинстве основных случаев из-за его связи с обучением полагаться на наши пальцы. Вместо того, чтобы разбивать меньшую 5, давайте разбиваем 7 и 8 на куски.Семерка — это горстка плюс еще два пальца; 8 — небольшой плюс три пальца. Итак, 5 + 7 легко увидеть как две горстки (10) плюс 2 больше, равно 12 . Аналогично, 5 + 8 рассматривается как две горстки (10) плюс еще 3, равно 13 . Красивый!
и nbsp
*** Резюме ***Вот таблица сложения:
+0 +1 +2 +3 +4 +5 +6 +7 +8 +9
-----------------------------
0 | 0 1 2 3 4 5 6 7 8 9
1 | 1 2 3 4 5 6 7 8 9 10
2 | 2 3 4 5 6 7 8 9 10 11
3 | 3 4 5 6 7 8 9 10 11 12
4 | 4 5 6 7 8 9 10 11 12 13
5 | 5 6 7 8 9 10 11 12 13 14
6 | 6 7 8 9 10 11 12 13 14 15
7 | 7 8 9 10 11 12 13 14 15 16
8 | 8 9 10 11 12 13 14 15 16 17
9 | 9 10 11 12 13 14 15 16 17 18
Вместо того, чтобы пробивать его столбец за столбцом, я предложил более удобный подход, от простого к сложному.Вот оно снова, в сжатом виде.
- PLUS 0: добавление нуля ничего не меняет!
- 0 + 0, 1 + 0, 2 + 0. . . 9 + 0
- PLUS 1: , конечно, на следующий номер.
- 1 + 1, 2 + 1, 3 + 1. . . 9 + 1
- PLUS 2: шаг до следующего четного или нечетного.
- 2 + 2, 3 + 2, 4 + 2. . . 9 + 2
- 5 ПЛЮС МАЛЕНЬКОЕ ЧИСЛО: как счет на пальцах.
- МАЛЕНЬКИЕ ДВОЙКИ: как высвечивание одинакового количества пальцев на каждой руке.
- ПАРЫ, КОТОРЫЕ ДЕЛАЮТ 10: очень важными! Остальные:
- ПАРЫ, КОТОРЫЕ ДЕЛАЮТ 11: мгновенно воспринимаются как на 1 больше, чем пара, составляющая 10.
- БОЛЬШИЕ ДВОЙНИКИ: дает эвенов от 10 до 20.
- 9 ПЛЮС НИЧЕГО: «выпустите один, поставьте 1 впереди».
- 9 + 3, 9 + 4, 9 + 5, 9 + 6, 9 + 7, 9 + 8
- ЛЕВЫЕ: , если запоминание является проблемой.. .
- 4 + 3 — проблем быть не должно.
- 6 + 3 — думаю, 3-6-9 «счет по тройкам» последовательность.
- 8 + 4 — увеличить на 2 до 10; затем еще от 2 до 12.
- 8 + 6 — четное число, не намного превышающее 10.
- 6 + 7 — двойная 6 плюс 1.
- 7 + 8 — ровно посередине между 10 и 20.
- 7 + 5 — думайте большое число последним, 5 + 7; рассматривается как 5 + 5 + 2; две горсти (10) плюс еще 2.
- 8 + 5 — думайте большое число последним, 5 + 8; рассматривается как 5 + 5 + 3; две горсти (10) плюс еще 3.
& nbsp
Поздравляем! Теперь вы — счетчик !
& nbsp
Свяжитесь с Дональдом Саутером: отправьте электронное письмо; просмотреть гостевую книгу; подписать гостевую книгу.
Вернуться на главную страницу Дональда Саутера.
Лучше делать покупки, чем думать? Посетите «Мой маленький магазинчик редких и драгоценных товаров».
Вернуться к началу страницы.

 Нейрогимнастика. 8 листов.
Нейрогимнастика. 8 листов.
 Замер скорости и правильности решения примеров. Двузначные и трёхзначные флеш-карты. Счёт в сотне, состав числа второго десятка, сотни. Работа с монетной системой. Развитие обеих рук. Логика. Развитие внимания и пространственного мышления. Нейрогимнастика. 8 листов.
Замер скорости и правильности решения примеров. Двузначные и трёхзначные флеш-карты. Счёт в сотне, состав числа второго десятка, сотни. Работа с монетной системой. Развитие обеих рук. Логика. Развитие внимания и пространственного мышления. Нейрогимнастика. 8 листов. Графомоторика в клетке. 8 листов.
Графомоторика в клетке. 8 листов.:format(png)/c8c454a06142409.s2.siteapi.org/img/8ueleav7bn0o8sw8s8s08kck8cw40o) Формулы: +2=+5-3; Однозначные, двузначные; Трехзначные без новых формул. Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов.
Формулы: +2=+5-3; Однозначные, двузначные; Трехзначные без новых формул. Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов. Однозначные, двузначные; Трехзначные без новых формул. Понятие умножение. Умножение через сложение. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов.
Однозначные, двузначные; Трехзначные без новых формул. Понятие умножение. Умножение через сложение. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов. д.)
д.)
 Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов.
Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов. 8 листов.
8 листов. Закрепление формул друга и переходов через 50, 100. Повторение всех формул «Помощь брата и друга». Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Каллиграфия чисел. 8 листов.
Закрепление формул друга и переходов через 50, 100. Повторение всех формул «Помощь брата и друга». Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Каллиграфия чисел. 8 листов.:format(png)/e5d928e195f8476.s2.siteapi.org/img/tqn203qimjkgcww0k0wgwckw0gwos4) д.)
д.) Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.
Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.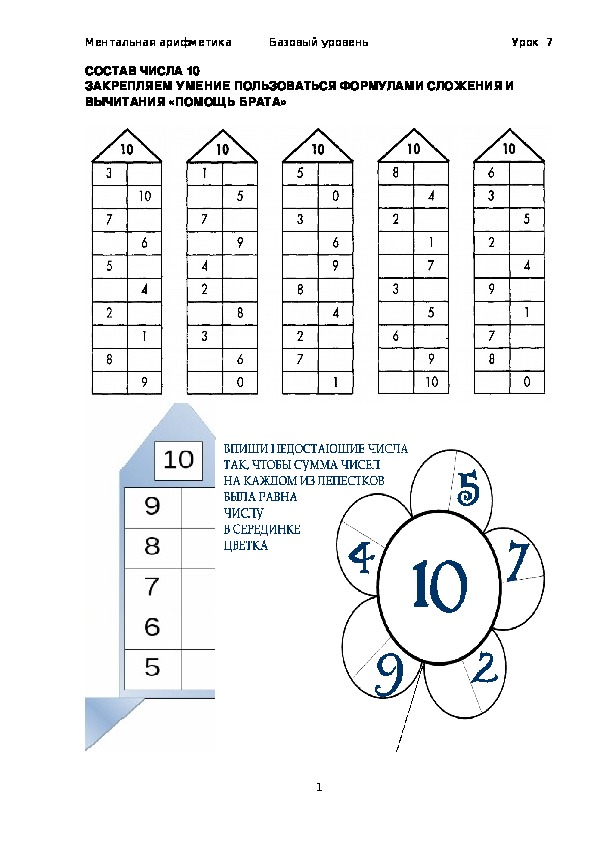 д.)
д.)-750x750.jpeg) 8 листов.
8 листов. Сложение/вычитание анзан. (4 стр.)
Сложение/вычитание анзан. (4 стр.) д.)
д.):format(png)/e5d928e195f8476.s2.siteapi.org/img/skbutjqpciogokwwo4cgsc08sgkcg0) Умножение и сложение/вычитание анзан. (4 стр.)
Умножение и сложение/вычитание анзан. (4 стр.) (16 стр.)
(16 стр.) д.)
д.)