Ментальная Арифметика Сложение
Урок № 2. Ментальная Арифметика Сложение.
После необходимой всем начинающим тренировки беглости пальцев можно приступать к выполнению одного из простейших вычислений — сложению. У него есть только один способ. Для того чтобы нагляднее его представить, начнем с простого примера.
Пример 1
Отложим на счетах число 21.

Возьмем ряд G и соседний с ним. Понятно, что число 2 откладывается на ряду G, а 1 на Н, так как числа откладываются слева направо, начиная с большего разряда. Впредь число 21 — число отсчета или базовое число. (Стоит заметить, почему были выбраны именно эти ряды. Дело в том, что их расположение цифр на них сходно с положением цифр на обычном электронном калькуляторе, поэтому не стоит усложнять задачу.)
А теперь прибавим к базовому числу 6.

Мы видим, что эта задача решена, если отложить на счетах всего две косточки — на верхнем ряду косточка опускается вниз (что означает прибавление к числу 21 пяти) и откладыванием вверх еще одной косточки (в сумме с они образуют 6). Не стоит забывать что все эти преобразования происходят в ряду Н, так как он является рядом меньшего разряда.
Путем зрительной памяти не сложно определить, что получается при выполнении сложения — суммой 21 и 6 является число 27.
Продолжим суммирование. Для примера нередкой ситуации «вычитания в сложении» прибавим к полученному числу 27 (теперь оно — базисное) 15. Для этого в ряд G добавляем одну косточку, которая символизирует «1» в 15.

Осталось лишь прибавить «5» из числа 15. Но так как в ряду Н уже существует 7, то необходимо поступить следующим образом: косточку в верхнем отделении поднимают, «отнимают 5», но тут же прибавляют косточку в нижнем отделе следующего разряда «прибавляют
10» в ряду G. Это ключевой момент в сложении на соробане, когда косточек для сложения на
данной линейке не хватает — прибавляют одну косточку к старшему разряду (внизу) и отнимают необходимое количество на данной линейке. Сначала надо делать движения на младшей линейке (H), затем на старшей(G)
Видно, что получается число 42, которое и будет являться суммой чисел 27 и 15.

Пример 2
В качестве подобного примера, для закрепления ситуации «вычитания в сложении», возьмем следующий несложный пример.
Отложим на счетах число 14 (работа начинается, прежде всего, со сброса предыдущего примера; она продолжается в тех же рядах — Н и G).

Работая слева направо, откладываем одну косточку на ряду G, и четыре — на ряду Н. На первый взгляд прибавление к 14 единицы не составит труда. Однако выполнение этой задачи на соробане требует логического мышления и тренировки. Итак, для того чтобы решить пример 14+1 следует работать с рядом Н (ведь именно он — меньший разряд), причем отложив косточку в верхнем ряду, а четыре косточки в нижнем ряду сбрасываются.
Мы можем видеть результат: 14+1=15

Пример 3
Отлично, теперь решим задачу потруднее. Не несколько цифр, а общие действия слева направо в многозначном числе. Давайте попробуем 3345+6789 (=10134)
Для начала отложим 3345 в окне соробана:

Следующим шагом, мы должны «прибавить 6» из 6789 на линейке Е.

Получили число 9345 , это не окончательный ответ, мы должны прибавить еще три числа! Следующий шаг «прибавить 7» на линейке F. здесь как раз тот случай, когда надо подумать. Представим себе, что мы «Прибавим 10 и отнимем 3» это тоже самое, что «прибавим 7». Мы должны передвинуть три косточки вниз на линейке F (отнять 3), а затем передвинуть вверх 1 косточку (прибавить 10 ) на линейке Е. Но там нет возможности добавить косточку, поэтому добавляем ее на следующей линейке слева, а переполненную линейку сбрасываем. Это и есть ключевая концепция соробана.
Результат в следующем окне:

Это число 10045. Но это не все. Еще есть два числа. Как вы видите, осталось повторить процесс сложения — и на практике это получается довольно просто. Следующим шагом мы должны «прибавить 8» на линейке G. Снова не хватает косточек. И здесь мы должны «Отнять 2, прибавить 10». Следовательно, мы должны опустить две косточки на G и поднять одну косточку на линейке F.
Результат в следующем окне:

Теперь имеем число 10125. Берем для сложения последнюю цифру «9». Мы должны добавить 9 на линейке H. Опять не хватает косточек и мы должны по старой схеме «прибавить 10, отнять 1» Для вычитания 1 на линейке Н мы должны «Отнять 5» и «прибавить 4». Не забудем теперь, что мы должны еще прибавить 1 на линейке G. После выполнения этого шага теперь получаем следующую картину:

Видно, что это число 10134, что является суммой чисел 3345+6789 Много проще и аккуратнее, чем вы бы делали это на бумаге.
[SWF]http://mentalar.ru/wp-content/uploads/2017/09/000.swf,700,500[/SWF]
Автор публикации
40 Комментарии: 15Публикации: 397Регистрация: 06-06-2017Ментальная Арифметика Вычитание
Урок № 3. Ментальная Арифметика Вычитание.
Вычитание на соробане такое же простое как и сложение, это обратный процесс. Вместо переносов на десятки (следующая линейка слева), теперь придётся занимать с этой же самой линейки. В целом для вычитания стиль работы с примерами и числами слева направо — по одной линейке. Если на текущей линейке у вас не хватает косточек для вычитания нужного числа — вы должны отнять «1» от старшего разряда (слева) а на текущий добавить разницу. Мы хотим дать конкретный пример для демонстрации простоты процесса.
Возьмем число 47:

И вычтем из него 21. Начинаем с линейки G и «вычитаем 2» простым перемещением 2 косточек вниз.
Теперь мы имеем значение 27 (но это еще не конец)

Теперь переходим к единичной линейке и «Отнимаем 1» перемещением одной нижней косточки вниз. Здесь имеем конечный ответ 26.

Теперь отнимем 4 из этого. Мы должны перейти на единичную линейку и «Отнять 4», но так как в нижней ее части не хватает косточек для такого вычитания, заменяем действия на «Отнять 5, прибавить 1». Для выполнения этого отодвигаем верхнюю косточку от перегородки, а снизу добавляем одну. Имеем ответ 22. (Это результат вычитания 26- 4):

Теперь продемонстрируем способ «заёма». Возьмем 22 на соробане и отнимем 14. Сначала отнимем 1 на линейке G, это просто. Наш результат (не конечный) будет:

Теперь мы должны «Отнять 4» на единичной линейке H. Так как мы не имеем достаточно косточек, мы должны заменить действие на » Отнять 10, прибавить 6″ для получения того же результата. Отодвинем одну нижнюю косточку на линейке G (надо помнить, что каждая косточка на линейке слева «весит» 10 единиц относительно той линейки, что справа) и «прибавим 6» на линейке H. Для этого придвинем к перегородке одну косточку сверху, одну снизу(5+1=6). Результат на соробане 8 — это и есть ответ!

[SWF]http://mentalar.ru/wp-content/uploads/2017/09/000.swf,700,500[/SWF]
Автор публикации
40 Комментарии: 15Публикации: 397Регистрация: 06-06-2017
|
Ментальная Арифметика Умножение
Урок № 4. Ментальная Арифметика Умножение.
Умножение есть не что иное как многократное сложение. Но вместо того, что бы 23 раза прибавлять одно и тоже число, легче выполнить его умножение. Существует особая техника выполнения умножения в окне соробана. Есть несколько различных методов. Здесь приводится метод, который был рекомендован Японским Комитетом по Абакусу. Этот метод считается дающим меньше ошибок и простым в обучении.
Теперь поставим перед собой задачу умножения 23Х47. Число 23 будет называться множимым, а число 47 — множителем. Прежде всего расположим множимое (а это число 23) вблизи центра счетной доски. Пропустив пустую линейку, число 47 (множитель) расположим слева
Между числами пропущены линейки для лучшей наглядности, при не таких маленьких счетах можно пропускать и больше.

Процесс умножения подобен тому, как мы делаем это на бумаге, но отличается последовательностью выполнения действий
Сначала берем правую цифру множимого ( 3) и умножаем на крайнюю левую цифру множимого 3×4=12. Число 12 откладываем слева от множимого (на линейках FG)

затем эту же цифру множимого умножаем на следующую слева направо цифру множителя 3×7=21, получившееся число 21 прибавляем к результату, но уже сдвинув вправо на один разряд (линейки GH ) :

Теперь мы не нуждаемся в цифре 3, так как с ней уже все проделано, очистим эту линейку (E ) для дальнейшей работы
Теперь берем следующее число множимого — в нашем случае это 2. Умножаем его на левую крайнюю цифру множителя. Результат (2×4=08) прибавляем к линейкам EF. Поскольку в общем случае результат занимает 2 разряда, одноразрядный результат надо представлять в виде 08, что бы правильно разместить его на линейках, так получается следующая картина:

В заключение мы должны умножить 2 на оставшуюся цифру множителя 7 и получившийся результат 14 прибавить на линейки FG
К линейке F надо прибавить 1, но она полностью заполнена, поэтому по правилам сложения, прибавляется 1 к следующему разряду (E), а здесь отнимается 9. Затем к линейке G прибавляется 4

получившееся число является результатом действия 23×47=1081
[SWF]http://mentalar.ru/wp-content/uploads/2017/09/000.swf,700,500[/SWF]
Автор публикации
40 Комментарии: 15Публикации: 397Регистрация: 06-06-2017Мастер-класс по ментальной арифметике «Нестандартное решение примеров»
Мастер-класс
по теме:
«Нестандартное решение примеров.
Знакомство.
Математические вычисления»
Учитель: Барадулина Л.Ю.
Цель урока: отработать навык простого сложения и вычитания. Научиться применять полученные навыки в ментальном счете.
Задачи урока: закреплять умение выполнять операции на прямое сложение и вычитание без перехода через разряд (простое сложение и вычитание), учить считать, используя ментальную карту и ментально, тренировать навык решения смешанных примеров на сложение и вычитание, складывать и вычитать по цепочке три и четыре числа ментально, развивать память, внимание, воображение.
— обучающийся научиться выполнять смешанные операции на прямое сложение и вычитание без перехода через разряд
обучающийся научиться считать используя ментальную карту и ментально
обучающийся научиться складывать и вычитать три и четыре числа ментально
обучающийся продолжит развивать память, внимание, логическое мышление
Формируемые УУД
Познавательные
умение работать по иллюстрациям; становление причинно — следственных связей и др.
Регулятивные
умение осуществлять действие по образцу и заданному правилу; заданную цель; умение сохранять заданную цель; умение адекватно понимать оценку педагога и обучающихся; умение работать по инструкции педагога
Коммуникативные
умение вести монолог, отвечать на вопросы; умение организовывать совместную
деятельность в парах, в подгруппе и в коллективе; Умение взаимодействовать и сотрудничать с учителями-учениками и педагогом
Знакомство.
Приветствуем аудиторию, знакомимся;
Интересуемся, что присутствующим известно о том, что даёт ментальная арифметика;
Объясняем пользу МА по пунктам:
Гармоничное развитие обоих полушарий головного мозга;
Быстрый устный счёт.
История соробана его строение
Не опровергнутые историками ресурсы говорят о появлении абака в Месопотамии в 3 тысячелетии до нашей эры и в Древнем Риме с 5 века до н.э. Более достоверное доказательство — образец абака и чертёж, выполненный европейцем – хранятся в Кабинете медалей Парижской национальной библиотеки и датируются 17 веком. О
китайском варианте абака — Суаньпане упоминается в национальной литературе в 190-м году. Китайцы превратили табличку в привычную рамку со стержнями и
косточками. В «небесном» окошке размещалась не одна, а две косточки. В таком виде счёты прибыли в Японию с развитием мореплавания. Японцы убрали дополнительную небесную косточку, и назвали счёты соробаном (вычислительной доской). Так как торговля в стране в это время начинала активно развиваться, важность математического образования была очень высока. Подверженный тщательному изучению, множеству усовершенствований, соробан принял современный вид.
Тренировочные упражнения на соробане.
Постановка техники рук.
Постановка техники рук.
Существуют различные техники счёта — одной рукой, двумя руками (показать).
Ассиметричная постановка пальцев приводит к тому, что каждый решенный пример, по сути, является упражнением для развития межполушарных связей.
Чистка соробана. (упражнение «Уточка»)
Правила набора чисел (0-9).
Кинезиологическая гимнастика (для ладони и ушей)
Кинезиология – наука о развитии умственных способностей через движения.
ФУ по набору этих чисел с проговариванием.
Фундаментальные упражнения — специальные упражнения, которые развивают мелкую моторику, одновременно закрепляют новую тему и способствуют развитию скорости мышления.
(Важно уделить внимание постановке пальцев левой руки, тщательно проработать ФУ для левой руки.)
Игры на внимание с флеш-картами. Числа от 0 до 9
Работа «в тетрадях»
Набор чисел на соробане от 0 до 9
Убедиться в том, что обучающие различают числа от 1 до 9 на соробане
Флеш-карты (развитие фотографическую память). Запись чисел по флеш-картам
Закрасить косточки чтобы получилось указанное число.
Скорость письма. (развитие скорости письма)
Запись цифр 0 -9 за 1 мин.
Работа по развитию скорости мышления ведется постоянно через установку нормативов. Они позволяют повышать скорость вычисления примеров постепенно, в комфортных для детей условиях.
Проверка. Запись результатов.
Фундаментальные упражнения. (развитие мелкой моторики)
Примеры
1+5 8-5 2+5 7-5 3+5 6-5 4+5 5-5 9-5
Важно обратить внимание на постановку пальцев, тщательно следить за правильным выполнением ФУ.
Прямое сложение и вычитание (+6,-6)
Примеры
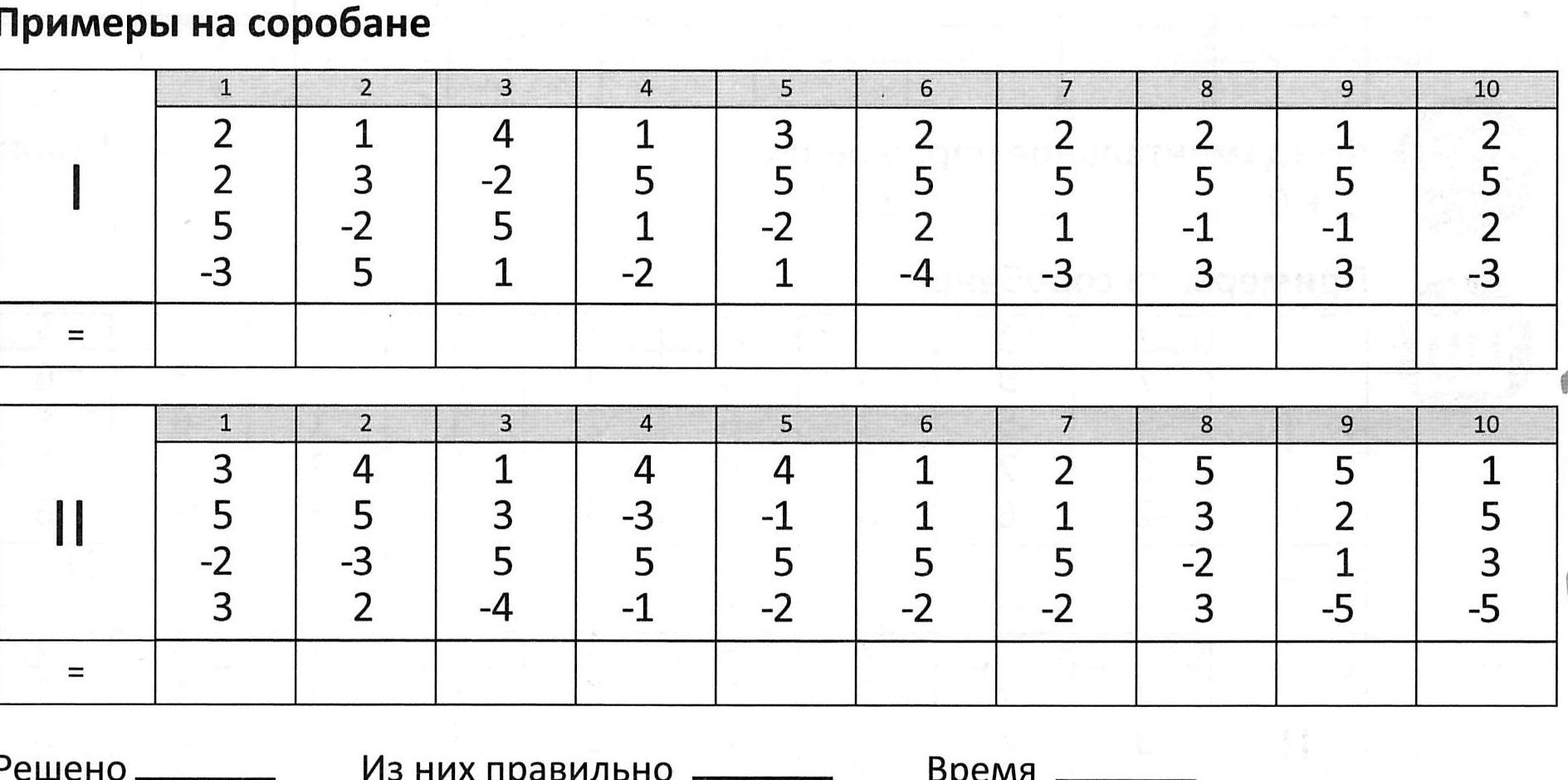
Результаты проверяем сразу. Запись результатов.
Ментальный диктант.
Что такое ментальный счет. Учителя двигают пальчиками на столе, перемещая воображаемые косточки. Запись ответов. Взаимопроверка
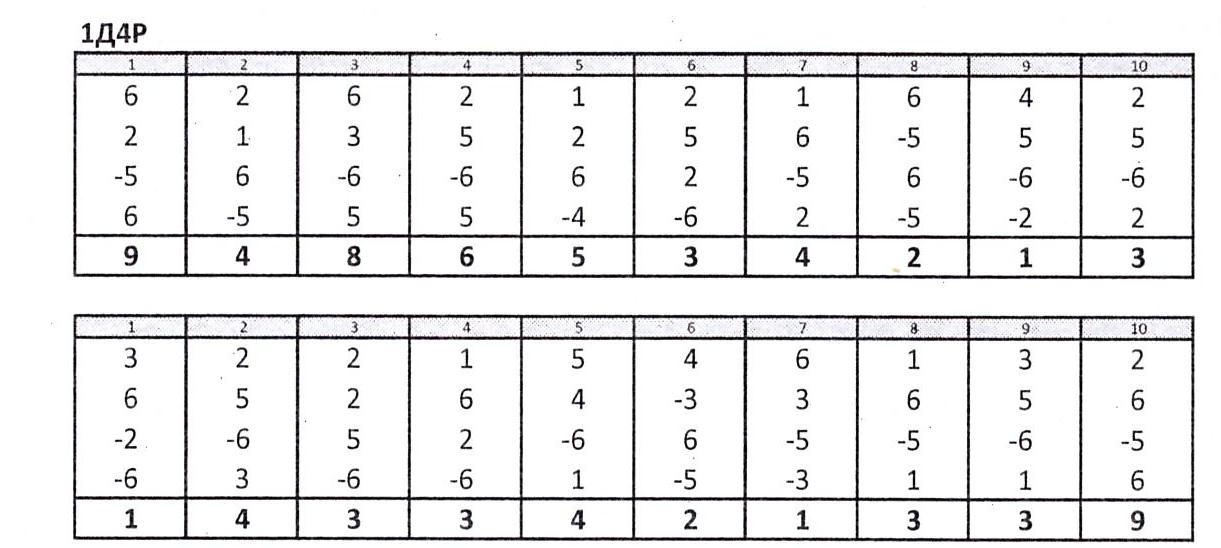
Рефлексия
Цель: соотнести поставленные задачи и полученные результаты
оценка деятельности педагога
Рефлексияда
нет
1
На занятии я:
Я знаком(а) с этой программой
научился считать на абакусе простые примеры
научился решать примеры с применением формулы +-4
ничего не понял(а)
2
Мне понравилась:
работа на абакусе
работа по флеш-картам
3
Выводы:
меня заинтересовала программа
мне это не интересно
4
Оцените проведение мастер-класса
по 5-бальной системе
Просмотр видео-ролика «Что дает Ментальная арифметика»
Вычитание с помощью пятерки в Ментальной Арифметики
Мы закончили тему «Сложение с помощью пятёрки». Не забывайте каждый урок выполнять базовые упражнения. Это имеет большое значение в формировании моторного навыка.
Следующую тему- вычитание с помощью пятёрки — мы начнём сформулы −4, так как пройдя формулу +4, детям будет проще понять обратное действие.
Вычитание с помощью пятёрки
Объясняем принцип вычитания на примере формулы −4=-5+1
Если мы хотим вычесть из пятёрки четыре, то нам придётся отнять пятёрку, а друга четвёрки — единицу- прибавить.
И так, первая формула в теме «Вычитание с помощью пятёрки»:
-4=-5+1
Формула Базовые упражнения
-4=-5+1 5-4 6-4 7-4 8-4
На соробане / абакусе выполняется одним движением: указательный палец поднимает пятёрку, одновременно большой палец поднимает одну косточку.
8-4 =-5+1
В случае с вычитанием, действует тот же принцип — куда идёт пятёрка, в ту же сторону идёт друг числа, которое мы отнимаем. Так же обращаем внимание детей на то, что у пятёрки тот же знак, что и в действии, которое мы выполняем. Если в примере +, то пятёрка прибавляется, а за ней идёт друг. Так мы поможем детям не запутаться со знаками.
Закрепляем правило решением упражнений из рабочей тетради.
Следующая формула на вычитание:
-3=-5+2
Формула Базовые упражнения
-3=-5+2 5-3 6-3
7-3
На соробане/ абакусе выполняется одним движением: указательный палец поднимает пятёрку, одновременно большой палец поднимает две косточки.
7-3 =-5+2
5-3=-5+2
Закрепляем правило решением упражнений из рабочей тетради. Следующая формула:
-2=-5+3
Формула Базовые упражнения
-2=-5+3 5-2 6-2
На соробане/ абакусе выполняется одним движением: указательный палец поднимает пятёрку, одновременно большой палец поднимает три косточки.
5-2=-5+3 6-2=-5+3
Закрепляем правило решением упражнений из рабочей тетради.
-1=-5+4
Формула Базовые упразднения
-1=-5+4 5-1
На соробане выполняется одним движением: указательный палец поднимает пятёрку, одновременно большой палец поднимает четыре косточки.
5-1 =-5+4
Закрепляем правило решением упражнений из рабочей тетради .
Мы изучили все формулы сложения и вычитания с помощью пятёрки. Теперь необходимо закрепить навыки, решая примеры, где все пройденные формулы встречаются вперемежку. Решаем примеры из рабочей тетради на странице 36.
Следующая большая тема — помощь десятки — требует работы двух рук. И к этому времени, с помощью разминок и базовых упражнений, выполняемых двумя руками, мы должны подготовить левую руку (у левшей правую) к работе. Кстати, левши на абсолютно равных условиях занимаются ментальной арифметикой, так как руки при счёте на соробане / абакусе работают одинаково, за исключением того факта, что левши держат карандаш в левой руке, а правши в правой.
Перед тем, как начать изучение формул с помощью десятки, необходимо выучить состав числа десять, аналогично тому, как мы это делали с пятёркой.
В числе десять друзья -следующие пары чисел: 1 и 9, 2 и 8, З и 7, 4 и 6, 5 и 5.
Эти пары нужно хорошо закрепить, в том числе, включая их в занятия письмом, и после этого мы начинаем следующую тему.

