Плюсы и минусы в математике: Сложение и вычитание отрицательных и положительных чисел. Решение примеров. – Правила знаков

Сложение и вычитание отрицательных и положительных чисел. Решение примеров.

Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.

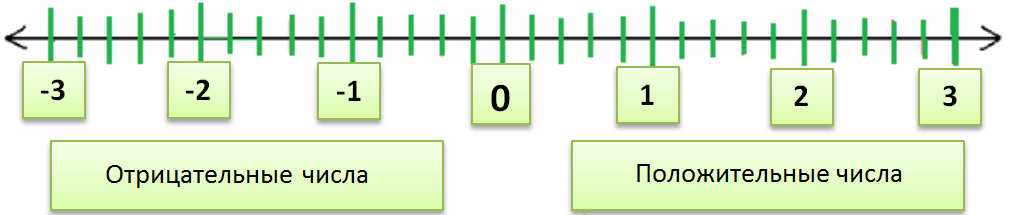
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:

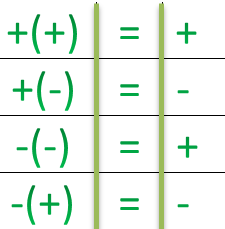
• Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.

\((-2)+(-3)=-5\)

• Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:

\((-8)+4=4-8=-4\)

\(9+(-4)=9-4=5\)

Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:

\(-9+9=0\)     \(7,1+(-7,1)=0\)

• При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

\((-7)-(-6)=(-7)+6=(-1)\)

• Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.

\(7-9=-2\) так как \(9>7\)

• Также не стоит забывать минус на минус дает плюс:

\(7-(-9)=7+9=16\)

Задача 1. Вычислите:

 

1.  \(4+(-5)\)
2.  \(-36+15\)
3. \((-17)+(-45)\)
4. \(-9+(-1)\)

 

Решение:

 

1.  \(4+(-5)=4-5=-1\)
2.  \(-36+15=-21\)
3. \((-17)+(-45)\) \(=-17-45=-62\)
4. \(-9+(-1)=-9-1=-10\)

Задача 2. Вычислите:

1. \(3-(-6)\)
2.  \(-16-35\)
3. \(-27-(-5)\)
4.  \(-94-(-61)\)

Решение:

1.  \(3-(-6)=3+6=9\)
2. \(-16-35=-51\)
3.  \(-27-(-5)=-27+5=-22\)
4.  \(-94-(-61)=-94+61=-33\)

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Правила знаков

Минус и плюс – это признаки отрицательных и положительных чисел в математике. Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.

Рассмотрим подробней основные правила знаков.

Деление.

Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».

Умножение.

Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс». Тоже самое касается и двух отрицательных чисел. Если мы умножаем «минус» на «минус», то получим «плюс».

Вычитание и сложение.

Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.

Правила при умножении (делении) чисел

Множители (делимое и делитель) Результат + + + + — — — + — — — +

Знаки плюса и минуса — Википедия

Знаки «плюс» и «минус» (+ и −) — математические символы, используемые для обозначения операций сложения и вычитания, а также положительных и отрицательных величин. Кроме того, они используются и для обозначения других понятий — например, в физике и химии знаками + и — обозначаются положительный и отрицательный заряд соответственно. Латинские термины

plus и minus означают «более» и «менее» соответственно.

Знаки, обозначавшие сложение и вычитание, были ещё у древних египтян. Египетский иероглифический символ, внешне похожий на пару ног, в одном направлении обозначал сложение, в другом направлении — вычитание^[1]

или

.

Французский математик XIV века Николай Орем в своих работах уже использовал знак плюс «+»^[2], но эта практика не получила распространения среди его современников. Труды европейских математиков начала XV века, как правило, используют латинские буквы «P» и «M» в качестве знаков «плюс» и «минус» соответственно

[3]. В трактате 1494 года Сумма арифметики (англ.)русск. итальянский математик Лука Пачоли вводит символы P с чертой — p̄ для più, то есть «плюс» и M с чертой — m̄ для meno, то есть «минус»^[4].

Знак «+» является упрощением латинского «ЕТ» (сравнимо со знаком амперсанда «&»)^[5], знак «−» может быть получен из знака тильды, который пишется над буквой «m», используемой для обозначения вычитания, или из варианта стенографической записи самой буквы «m»^[6]. Немецкий математик Иоганн Видман в своём трактате 1489 года использует символы «−» и «+», объясняя их как minus и mer (современный нем. Mehr — «больше»): «was − ist, das ist minus, und das + ist das mer»^[7].

Первое появление знаков «плюс» и «минус». Страница из книги Иоганна Видмана

Немецкий математик и теоретик музыки Генрих Грамматеус в своём трактате 1518 года также использует знаки «+» и «−» для обозначения сложения и вычитания^[8].

Английский математик Роберт Рекорд, который ввёл в научный оборот знак равенства, также ввёл в англоязычную традицию знаки плюс и минус в 1557 году в своём труде The Whetstone of Witte (англ.)русск.: «имеется два часто используемых знака, первый из которых пишется „+“ и означает „прибавить“; другой пишется „−“ и означает „вычесть“»^[9].

Знак плюс (+) является бинарным оператором, который указывает на операцию сложения, например, 31 + 5 = 36. Также может выступать унарным оператором, который оставляет свой операнд без изменений («+х» означает то же самое, что и «х»). Знак плюса может использоваться, когда необходимо подчеркнуть положительность числа в противоположность отрицательному (+5 против −5).

Знак плюс также может указывать на многие других операции. Многие алгебраические системы имеют операцию, которая называется или равнозначна сложению. Принято использовать знак плюса для коммутативных операций^[10].

Кроме того, плюс может также означать:

Знак минус (−) имеет три основных применения в математике^[11]:

1. Оператор вычитания: бинарный оператор, указывающий на операцию вычитания, например 36 − 5 = 31;
2. Как указатель отрицательных величин, например −5;
3. Унарный оператор, который действует в качестве инструкции для замены операнда на противоположное число. Например, если х = 3, то −x = −3;

аналогично, −(−2) равно 2.

В большинстве англоязычных стран именование отрицательных чисел происходит с использованием слова «минус» (например, «минус пять»), но в современном американском английском это число произносится как «отрицательное пять» и эта форма рекомендуется как правильная; слово «минус» в данном контексте обычно используют люди, родившиеся до 1950 года

[12]. Кроме того, некоторые учебники в США рекомендуют запись «−х» читать как «противоположность х» или «число, противоположное х», чтобы избежать впечатления, что −x непременно является отрицательным^[13].

В языке программирования APL и некоторых графических калькуляторах (например, TI-81 и TI-82) для обозначения отрицательных чисел используется поднятый знак минус (например, 36 − 55 = ⁻19), но такое использование является редкостью.

В математике и большинстве языков программирования, порядок действий устанавливает, что −5² = −25: унарный оператор (минус) имеет приоритет перед операциями умножения или деления. При этом в некоторых языках программирования и Microsoft Excel, в частности, унарные операторы имеют приоритет и в других случаях, например (−5)² = 25, но 0−5² = −25^[14]

.

Плюс, минус и дефис.

Наименование	Обозначение	Unicode	ASCII	В URL	HTML
Плюс	+	U+002B	+	%2B
Минус	−	U+2212		%E2%88%92	− − −
Дефис	—	U+002D	-	%2D
Большой плюс	＋	U+FF0B		%EF%BC%8B	＋ ＋
Тире	－	U+FF0D		%EF%BC%8D	－ －

1. ↑ Karpinski, Louis C. Algebraical Developments Among the Egyptians and Babylonians (англ.) // The American Mathematical Monthly : journal. — 1917. — Vol. 24, no. 6. — P. 257—265. — DOI:10.2307/2973180.
2. ↑ The birth of symbols — Zdena Lustigova, Faculty of Mathematics and Physics Charles University, Prague Архивировано 8 июля 2013 года.
3. ↑ Stallings, Lynn. A brief history of algebraic notation (неопр.) // School Science and Mathematics. — 2000. — May.
4. ↑ Sangster, Alan; Stoner, Greg; McCarthy, Patricia. The market for Luca Pacioli’s Summa Arithmetica (англ.) // Accounting Historians Journal (англ.)русск. : journal. — 2008. — Vol. 35, no. 1. — P. 111—134 [p. 115].
5. ↑ Cajori, Florian. Origin and meanings of the signs + and — // A History of Mathematical Notations, Vol. 1 (англ.). — The Open Court Company, Publishers, 1928.
6. ↑ Wright, D. Franklin. Intermediate Algebra / D. Franklin Wright, Bill D. New. — 4th. — Thomson Learning, 2000. — P. 1. — «The minus sign or bar, — , is thought to be derived from the habit of early scribes of using a bar to represent the letter m».
7. ↑ «plus». Oxford English Dictionary. Oxford University Press. 2nd ed. 1989.
8. ↑ Earliest Uses of Various Mathematical Symbols
9. ↑ Cajori, Florian (2007), A History of Mathematical Notations, Cosimo, с. 164, ISBN 9781602066847, <https://books.google.com/books?id=rhEh8jPGQOcC&pg=PA164> .
10. ↑ Fraleigh, John B. A First Course in Abstract Algebra (неопр.). — 4. — United States: Addison-Wesley, 1989. — С. 52. — ISBN 0-201-52821-5.
11. ↑ Henri Picciotto. The Algebra Lab (неопр.). — Creative Publications. — С. 9. — ISBN 978-0-88488-964-9.
12. ↑ Schwartzman, Steven. The words of mathematics (неопр.). — The Mathematical Association of America, 1994. — С. 136.
13. ↑ Wheeler, Ruric E. Modern Mathematics (неопр.). — 11. — 2001. — С. 171.
14. ↑ Microsoft Office Excel Calculation operators and precedence (неопр.). Дата обращения 29 июля 2009. Архивировано 11 августа 2009 года.

Плюс (+) Минус (−) Знак умножения (· или ×) Знак деления (: или /) Обелюс (÷) Знак корня (√) Факториал (!) Знак интеграла (∫) Набла (∇) Знак равенства (=, ≈, ≡ и др.) Знаки неравенства (≠, >, < и др.) Пропорциональность (∝) Скобки (( ), [ ], ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩) Вертикальная черта (|) Косая черта, слеш (/) Обратная косая черта, бэкслеш (\) Знак бесконечности (∞) Знак градуса (°) Штрих (′, ″, ‴, ⁗) Звёздочка (*) Процент (%) Промилле (‰) Тильда (~) Карет (^) Циркумфлекс (ˆ) Плюс-минус (±) Знак минус-плюс (∓) Десятичный разделитель (, или .) Символ конца доказательства (∎)

Знак плюс-минус — Википедия

Материал из Википедии — свободной энциклопедии

∓

±

Знак плюс-минус (±) — математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и отрицательным. Часто используется, например, для указания:

• пределов изменения каких-либо параметров;
• инструментальной точности измерения физической величины;
• ожидаемого разброса значений статистически измеренного параметра;
• интервала значений результата в приближённых математических вычислениях.

Пример 1: фраза «напряжение в сети должно быть 220 ± 4,5 вольт» означает, что напряжение должно быть в диапазоне от 215,5 до 224,5 вольт.

Пример 2, где символ «плюс-минус» надо понимать буквально, как указание альтернативы из двух вариантов — известная формула для вычисления двух корней квадратного уравнения ax2+bx+c=0{\displaystyle ax^{2}+bx+c=0}:

x=−b±b2−4ac2a.{\displaystyle \displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.}

Эта формула — компактная запись, объединяющая формулы для первого и второго корня:

x1=−b+b2−4ac2a;x2=−b−b2−4ac2a{\displaystyle \displaystyle x_{1}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}};\quad x_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}}

Пример 3, аналогичный второму, тригонометрический:

sin⁡(x±y)=sin⁡(x)cos⁡(y)±cos⁡(x)sin⁡(y){\displaystyle \sin(x\pm y)=\sin(x)\cos(y)\pm \cos(x)\sin(y)}

Пример 4. Здесь истолкование символа плюс-минус иное: надо выбрать знак одночлена в зависимости от его номера в ряду:

sin⁡(x)=x−x33!+x55!−x77!+⋯±1(2n+1)!x2n+1+⋯{\displaystyle \sin \left(x\right)=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \pm {\frac {1}{(2n+1)!}}x^{2n+1}+\cdots }

Знак плюс-минус появился у Альбера Жирара (1626), который записывал этот символ следующим образом: ou+−  {\displaystyle {\boldsymbol {{\underset {-}{\overset {+}{\operatorname {\scriptscriptstyle ou} }}}\ \ }}} (французское слово ou в переводе означает «или»). Современный вид символу придал Уильям Отред в 1631 году^[1].

У знака плюс-минус есть вариант: знак ∓{\displaystyle \mp } (минус-плюс). Он используется совместно с одним или несколькими знаками плюс-минус и означает, что знаку плюс в плюс-минусе строго соответствует знак минус в минус-плюсе, и обратно. Пример:

cos⁡(x±y)=cos⁡xcos⁡y∓sin⁡xsin⁡y{\displaystyle \cos(x\pm y)=\cos x\cos y\mp \sin x\sin y}

Это компактная запись двух формул:

cos⁡(x+y)=cos⁡xcos⁡y−sin⁡xsin⁡y; cos⁡(x−y)=cos⁡xcos⁡y+sin⁡xsin⁡y{\displaystyle \cos(x+y)=\cos x\cos y-\sin x\sin y;~\cos(x-y)=\cos x\cos y+\sin x\sin y}

В шахматной нотации символ ± означает, что после соответствующего хода преимущество имеют белые, а символ ∓ — что преимущество у чёрных.

Символ	Код в Юникоде	Название в Юникоде	Название	HTML шестн.	HTML десят.	HTML обозн.
±{\displaystyle \pm }	U+00B1	Plus-minus sign	Символ плюс-минус	±	±	±
∓{\displaystyle \mp }	U+2213	Minus-or-Plus sign	Символ минус-плюс	∓	∓

• В ISO 8859-1 символ плюс-минус имеет код 0xB1.
• В TeX знаки плюс-минус и минус-плюс кодируются как \pm и \mp соответственно.
• В системе Microsoft Windows для ввода символа плюс-минус можно, прижав клавишу Alt, ввести на цифровой клавиатуре число 0177.
• В системах Linux/Unix сформировать символ плюс-минус можно последовательностью compose +-.
• На компьютерах Макинтош плюс-минус кодируется вводом символов ⌥ Option ⇧ Shift = .

1. ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — С. 127. — 248 с. — ISBN 978-5-382-00839-4.

Плюс (+) Минус (−) Знак умножения (· или ×) Знак деления (: или /) Обелюс (÷) Знак корня (√) Факториал (!) Знак интеграла (∫) Набла (∇) Знак равенства (=, ≈, ≡ и др.) Знаки неравенства (≠, >, < и др.) Пропорциональность (∝) Скобки (( ), [ ], ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩) Вертикальная черта (|) Косая черта, слеш (/) Обратная косая черта, бэкслеш (\) Знак бесконечности (∞) Знак градуса (°) Штрих (′, ″, ‴, ⁗) Звёздочка (*) Процент (%) Промилле (‰) Тильда (~) Карет (^) Циркумфлекс (ˆ) Плюс-минус (±) Знак минус-плюс (∓) Десятичный разделитель (, или .) Символ конца доказательства (∎)

Как понять, почему «плюс» на «минус» дает «минус» ?

Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.

Законы математики

Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель…

Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».

Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.

Аксиома кольца

Существует несколько математических законов.

• Первый из них переместительный, согласно ему, C + V = V + C.
• Второй называется сочетательным (V + C) + D = V + (C + D).

Им же подчиняется и умножение (V х C) х D = V х (C х D).

Никто не отменял и правил, по которым открываются скобки (V + C) х D = V х D + C х D, также верно, что C х (V + D) = C х V + C х D.

Кроме того, установлено, что в кольцо можно ввести специальный, нейтральный по сложению элемент, при использовании которого будет верно следующее: C + 0 = C. Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.

Выведение аксиом для отрицательных чисел

Приняв приведенные выше утверждения, можно ответить на вопрос: «»Плюс» на «минус» дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.

Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа — V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.

Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.

Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.

Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V. Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).

Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.

Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.

Умножение и деление двух чисел со знаком «-»

Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.

Допустим, что C — (-V) = D, исходя из этого, C = D + (-V), то есть C = D — V. Переносим V и получаем, что C + V = D. То есть C + V = C — (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.

(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) — (C х V) = D.

Вспомная о правилах работы со скобками, получаем:

1) (-C) х (-V) + (C х V) + (-C) х V = D;

2) (-C) х ((-V) + V) + C х V = D;

3) (-C) х 0 + C х V = D;

4) C х V = D.

Из этого следует, что C х V = (-C) х (-V).

Аналогично можно доказать, что и в результате деления двух отрицательных чисел выйдет положительное.

Общие математические правила

Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья. Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.

Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.

Минус на минус даёт плюс. А почему?

Минус на минус даёт плюс – это правило, которые мы выучили в школе и применяем всю жизнь. А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.

С древних времён люди пользуются положительными натуральными числами: 1, 2, 3, 4, 5,… С помощью чисел считали скот, урожай, врагов и т.д. При сложении и умножении двух положительных чисел получали всегда положительное число, при делении одних величин на другие  не всегда получали натуральные числа – так появились дробные числа. Что же с вычитанием?  С детских лет мы знаем, что лучше к большему прибавить меньшее и из большего вычесть меньшее, при этом мы опять же не используем отрицательные числа. Получается, если у меня есть 10 яблок, я могу отдать кому-то только меньше 10 или 10. Я никак не смогу отдать 13 яблок, потому что у меня их нет. Нужды в отрицательных числах не было долгое время.

Только с VII века н.э. отрицательные числа использовались в некоторых счётных системах, как вспомогательные величины, которые позволяли получить положительное число в ответе.

Рассмотрим пример, 6х – 30 = 3х – 9. Чтобы найти ответ, необходимо члены с неизвестными оставить в левой части, а остальные — в правую: 6х – 3х = 30 – 9, 3х = 21, х = 7. При решении этого уравнения нам даже не встретились отрицательные числа. Мы могли бы члены с неизвестными перенести в правую часть, а без неизвестных — в левую: 9 – 30 = 3х – 6х, (-21) = (-3х). При деление отрицательного числа на отрицательное получаем положительный ответ: х = 7.

Что мы видим?

Действия с использованием отрицательных чисел должны привести нас к такому же ответу, что и действия только с положительными числами. Мы можем больше не думать о практической непригодности и осмысленности действий – они помогают нам решить задачу гораздо быстрее, не приводя уравнение к виду только с положительными числами. В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.

Со временем, после проведения длительных опытов и вычислений удалось выявить правила, которым подчиняются все числа и действия над ними (в математике они называются аксиомами). Отсюда и появилась аксиома, которая утверждает, что при умножении двух отрицательных чисел получаем положительное.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Почему минус на минус дает плюс?

«Враг моего врага — мой друг».

Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.

Давным-давно людям были известны только натуральные числа: 1, 2, 3, … Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.

Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.

В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).

Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.

Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.

Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.

Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.

Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).

В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.

Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.

Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:

• сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
• умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
• сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.

Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.

Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.

Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Значит, B = C.

Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.

Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).

Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.

А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.

Ответил: Евгений Епифанов