Митральная математика: Ментальная арифметика – что это такое? Как научиться ментальной арифметике в домашних условиях? – Ментальная Арифметика ( Что Это, Обучение, Формулы ) Пособия

Ментальная арифметика — что это и кому она нужна

Екатерина Илясова, психотерапевт. Руководитель центра развития интеллекта «Пифагорка» в Новокузнецке. Педагог по ментальной арифметике.

Общение со специалистами по ментальной арифметике началось с того, что меня пригласили присутствовать на занятии. Лера Ворошилова, одна из первых учениц «Пифагорки», занимается ментальной арифметикой больше четырех месяцев и с нетерпением ждет начала урока. Учебный класс — уютный и душевный, здесь все продумано до мелочей: стулья и парты регулируются по высоте, между ними много свободного пространства. Понятно, почему ребенок с таким энтузиазмом рвется сесть за свою парту: учебный класс располагает не только к работе, но и к игре.

Занятие уже началось. Лера с удовольствием отдает свою тетрадь на проверку и ждет результат. Она выполнила домашнее задание самостоятельно, но допустила несколько ошибок. Преподаватель не ругает Леру, а лишь предлагает девочке самой найти ошибку и исправить ее. Лера с интересом уходит в работу, а у меня появляется возможность задать вопросы преподавателю.

Воображение и счет

Ментальная арифметика — это методика, которая пришла к нам из Азии. В Японии это методика входит в обязательную общеобразовательную программу, и дети обучаются по ней столько, сколько хотят. В «Пифагорку» она пришла из Турции. Сейчас по России открыто больше 70 центров. Что же такое ментальная арифметика, и как работает эта методика?

— Быстрый счет в уме — это «побочный эффект» данной методики, — смеется педагог Екатерина Илясова. — Ценность в том, что у ребенка развивается не только левое полушарие, но и правое. На занятиях дети учатся использовать свое воображение. Оно нужно не только для того чтобы быстро считать, но и для многих других задач. Воображение необходимо детям для творческого мышления, для принятия нестандартных решений.

На занятиях дети учатся использовать свое воображение: в процессе обучения они формируют образ счетов соробан в уме, а потом — так же в уме — считают на них. Поэтому на многих видеороликах по теме видно, как дети совершают некие манипуляции пальцами, а затем выдают правильный ответ.

Ментальная арифметика и школьная математика

Математика как школьная дисциплина имеет мало общего с ментальной арифметикой, но это ничуть не мешает ребенку из «Пифагорки» успешно учиться в школе. Напротив, с помощью ментальной арифметики он знакомится с другой стороной этой сложной для многих науки.

— Часто к нам приходят дети, у которых уже есть установки насчет себя и своих отношений с математикой. Они говорят: «Математика это сложно», «Я математику не знаю», «Я не знаю таблицу умножения», «Я не люблю математику», — рассказывает Екатерина. — Но в процессе они обучаются счету в уме, сложению, вычитанию, умножению, делению, простым законам, которые дает и общеобразовательная система, но по-другому. Хотя здесь тоже есть свои правила и свои законы, свои сложности и даже очень непростые примеры.

Методика помогает развивать и наращивать объем нейронных связей в головном мозге и поэтому подходит не для всех, а только для детей от 4 до 16 лет, когда идет активное формирование клеток головного мозга.

В центре «Пифагорка» первое занятие бесплатное, оно проводится с диагностической целью. Педагогу важно понимать потребности ребенка и свои возможности, ответить на вопросы: «Могу ли я ребенка научить чему-то, готов ли он к образовательной деятельности, нет ли психологических проблем, связанных с обучением в принципе?»

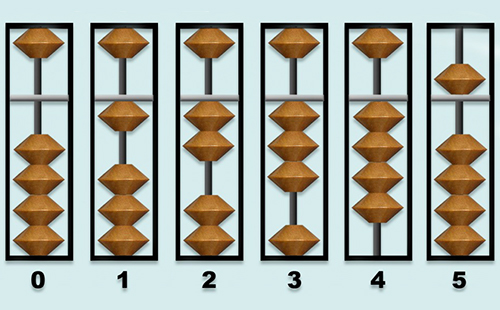
— Кроме этого, на первом занятии мы знакомим ребенка со счетами и числом пять, — объясняет Илясова. — Почему именно с этим числом? Потому что счеты соробан (иногда их еще называют «абак») не похожи на те счеты, что мы помним из детства. На них два поля, в которых расположены 13 или более спиц: в верхнем поле на спицы надето по одной косточке, в нижнем еще по 4. Таким образом, числа от одного до четырех — это единицы, а 5 — это уже отдельная косточка. 7 — это сочетание 5 и двух единичек. 9 — это 5 и четыре единички, и так далее. Это непросто понять взрослым, но малыши справляются легко.

Первые занятия посвящены знакомству со счетами как с предметом. Дети учатся работать с ними, выставлять правильно числа, считать на них. У ребенка формируется образ счетов в воображении, затем счеты постепенно убираются, и ребенок начинает совершать арифметические действия уже в уме.

Концентрация внимания и как ее достичь

— Перед началом каждого занятия я обязательно провожу зарядку. Их много и все они разные, но основная задача — научить детей концентрировать внимание. Ведь мы знаем, что недостаток внимания и есть самая большая проблема школьников. Такие зарядки особенно полезны при гиперактивности, — уточняет Екатерина. — Педагогам трудно работать с такими детьми, на них просто не хватает времени. Поэтому ребенок с гиперактивностью легко может стать лидером таблицы аутсайдеров. В нашем центре мы особое внимание уделяем такому ребенку. И, как правило, дети уходят с занятий спокойными, это и отзывы родителей подтверждают.

Тут Екатерина засекает время и говорит ученице: «Давай потренируем пальчики. Большим пальцем правой руки подними все косточки, а указательным левой опусти. Готово. А теперь одновременно двумя руками по направлению к центру опусти все косточки».

— Когда мы на время работаем со счетами — мы работаем сразу и с мелкой моторикой, и учимся концентрации внимания. Все это развивает мозг, — теперь Екатерина обращается уже ко мне. — Чем быстрее ребенок работает пальцами, тем быстрее он считает. При этом важно не путаться, какими пальцами нужно работать: большим поднимаем, указательным опускаем. Это надо держать в голове. Первое время дети путаются, а потом начинают делать автоматически.

Домашние задания: право на ошибку

— Домашние задания нужны ребенку для того, чтобы он постепенно научился самостоятельно справляться без помощи родителей. Дети не любят делать школьные задания, в том числе из-за страха совершить ошибку, — рассказывает педагог по ментальной арифметике Екатерина Илясова. — Я стараюсь сделать так, чтобы благодаря этим домашним заданиям у детей сформировалось ощущение, что они имеют право совершать ошибки. За ошибки я никогда не ругаю ребят и, что тоже важно, ничего не исправляю в тетрадях. Вы заметили, что у меня нет карандаша? Потому что ребенок в любом возрасте в состоянии осознать и исправить совершенную ошибку самостоятельно. Таким образом он учится сам себя контролировать и сам себя проверять.

Большинство родителей берут на себя слишком большую ответственность, контролируют домашние задания и жалуются на то, что очень устают от этого.

— Здесь мы учим, что ответственность за учебу и за результаты лежат только на ребенке, — продолжает Екатерина. — В «Пифагорке» домашние задания обязательны только для школьников. Я не требую неукоснительного выполнения домашних заданий. Дети, как правило, сами выполняют их с радостью и в конце урока спрашивают: «А домашнее задание будет?» Кстати, даже дошколята очень любят выполнять домашку. Объем заданий небольшой, но есть важное условие — родители не должны вмешиваться. Ребенок все делает только сам.

Английский, рисование и арифметика

Тем временем Лера исправила свои ошибки, и занятие продолжается. Екатерина предлагает ученице: «Посчитаем на счетах и по-английски до двадцати? One, two, three…»

Одновременный счет на счетах и вслух на английском языке задействует нейронные связи разных отделов головного мозга. Таким образом ребенок увеличивает объем памяти и расширяет кругозор.

— Я как мама понимаю, что каждый ребенок — личность со своими особенностями. Поэтому в нашем учебном центре главное и центральное место занимает личность ребенка, — объясняет Екатерина. — Особенно это касается дошкольников. Надо понимать, что они малыши и учиться им непривычно, поэтому мы используем много игровых приемов, но все они связаны с образовательным процессом. Некоторые игры могу предложить я, иногда дети сами являются генераторами идей. В голове у меня всегда есть план занятия, конструктор урока, но он гибкий, а значит, его легко подстроить под конкретного ребенка.

— Лера, а сейчас приступим к зарядке. Вытяни ручки вперед, соедини их в замок и рисуй ими знак бесконечности. Внимательно следи за большими пальцами. Очень внимательно следи.

Лера смеется, у нее не очень получается, она отвлекается.

— А если мы здесь нарисуем рожицы? — педагог рисует фломастером рожицы на ноготках. Лера смеется еще больше, но зато взгляд точно фокусируется именно на этих пальцах. Миссия выполнена!

— А теперь потри ушки пальчиками. Сверху вниз, снизу вверх, чтобы они стали теплыми.

Можно ли заниматься дома

Ментальная арифметика в домашних условиях — вполне реальное занятие. Для этого нужны счеты соробан, рабочие тетради и взрослый, который будет эту идею поддерживать. У методики масса своих особенностей, поэтому для начала освоить ментальный счет должен сам родитель.

— Мне известны случаи, когда мама проходила обучение методике и занималась со своим ребенком. Это возможно и реально. Просто вопрос — для чего мы это делаем? — рассуждает Екатерина. — Если дело только в навыке счета в уме, то, конечно, это можно делать дома. Было бы время у мамы и желание достичь цели. Развивающие центры дают детям больше, чем образование. Это и социализация, и личностный рост. Я считаю, что мама не должна быть педагогом своих детей. Я сама мама, и первыми моими учениками были мои дети. Но сейчас я передала их другому педагогу. Потому что детям сложно воспринимать маму как педагога, они не могут достичь того, что достигают другие. Кроме того, это правильно с точки зрения тех же границ — мама должна оставаться мамой.

Несмотря на естественную конкуренцию и развитие отношений в группе, дети соревнуются не друг с другом. Единственный человек, с которым они ведут спор — они сами. Сегодня они выполнили один объем работы, завтра сделают больше. Так они учатся ставить цели и добиваться их. А также формируют понимание, что сравнивать себя с другими — это пустое занятие. Мы никогда не станем кем-то. Только собой. У каждого из нас свой неповторимый рисунок жизни, и важно следовать своему заданному курсу.

Когда мы ориентируемся на других — мы тратим свою жизненную энергию не туда. И в результате сильно устаем и впадаем в депрессию.

— Поработаем в тетрадях. Лера, сколько за 15 минут ты сможешь выполнить заданий?

— Четыре страницы.

— Хорошо, начинаем.

Занятия для школьников и дошколят

Для каждого возраста в «Пифагорке» своя программа обучения. Это связано с тем, что у школьников уже сформирован образ числа. Но все дети учатся ментальному счету два года. В первый год изучают вычитание и сложение, во второй год — умножение и деление.

В конце каждого занятия педагог обязательно получает от ребенка обратную связь. Это очень важно, чтобы ребенок научился говорить о том, что он чувствует, называть свои эмоции, говорить о том, что не нравится. Уметь говорить о том, что не нравится — это важное качество. В дальнейшем детям становится проще понимать себя и свои потребности.

— Я все закончила.

— Лера, посмотри на время. 15 минут. Видишь, какая ты молодец? Ты поставила себе цель и выполнила ее. Понравилось тебе занятие? Какое у тебе сейчас настроение?

— Понравилось, но мне немножко грустно.

— Почему тебе грустно?

— Потому что занятие кончилось.

— Меня довольно часто спрашивают: ментальная арифметика — это развивающие занятия или полноценное обучение? Скажу так: развивайки, особенно, если речь идет о занятиях для детей от 6 месяцев — это в большей мере способ занять маму. Оценить результат очень сложно. Занятия веселые, разнообразные и интересные и помогают подготовить ребенка к детскому саду, — рассуждает Екатерина. — А ментальная арифметика — это совсем другое направление. Мы работаем с уже сформировавшейся личностью и помогаем ребенку в развитии его способностей. Занятия влияют на самооценку, на умение выстраивать коммуникацию, на самостоятельность, на усидчивость и концентрацию внимания. И самое приятное, что здесь можно получить ощутимый результат. Показатель — это не только навык счета в уме, но и интерес ребенка к учебе!

Справедливости ради надо сказать, что и отрицательные отзывы о ментальной арифметике тоже есть. Основная причина, по которой методика кого-то не устраивает — это боязнь перегрузить ребенка. Действительно, в 4 года малышу, не нужен навык складывания в уме трехзначных чисел. Но если ребенок сам проявляет интерес, а финансы родителей позволяют — почему нет? Главное, следить, чтобы занятия шли не через силу и не отбили у ученика тягу к дальнейшему обучению. Впрочем, этот совет касается не только ментальной арифметики, но и любых занятий с ребенком.

Митральный клапан — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 марта 2016; проверки требуют 10 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 марта 2016; проверки требуют 10 правок.

Митральный клапан
лат. valva atrioventricularis sinistra, valva mitralis
Схема сердца, спереди. Белыми стрелками указано направление кровотока в норме. Митральный клапан визуализируется справа
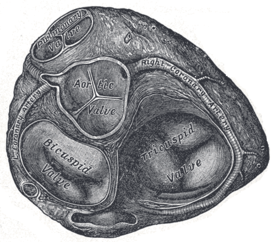Основание желудочков, предсердия удалены. Митральный клапан слева внизу
Медиафайлы на Викискладе

Митра́льный кла́пан (двустворчатый клапан) — ( лат. valve mitralis, valve atroiventicularis) клапан между левым предсердием и левым желудочком сердца. Представлен двумя соединительнотканными пластинками, которые предотвращают, во время систолы левого желудочка, регургитацию (обратный ток) крови в левое предсердие.

Двухстворчатый клапан (valvula bicuspidalis seu mitralis) состоит из двух больших створок — передней и задней. Число створок может колебаться от 3 до 6. Двухстворчатый клапан имеет форму овала, открытого вниз, влево и вперед. Продольный размер её составляет 23—37 мм, а поперечный 17—33 мм. Площадь клапана у новорождённого 1,18—1,49 см², у взрослого 4-6 см². Изменение данного показателя в меньшую сторону называется митральным стенозом, и в большую – недостаточностью^[2]. Передняя створка более развита, чем задняя. Линия прикрепления её к левому фиброзному кольцу располагается на 6 мм ниже самой нижней точки левой и задней створок клапана аорты. Во время систолы желудочка передняя створка выгибается в сторону левого венозного кольца и вместе с задней створкой закрывает его, а во время диастолы желудочка прилегает к межжелудочковой перегородке и закрывает аортальное отверстие. Задняя створка шире, чем передняя. Сухожильные хорды обеих створок отходят от двух больших сосочковых мышц.

1. ↑ ^{1 2} Foundational Model of Anatomy
2. ↑ Клапаны сердечно сосудистой системы: строение и физиология (рус.). Дата обращения 14 февраля 2019.

Математическая предметная классификация — Википедия

Математическая предметная классификация (МПК, англ. Mathematics Subject Classification, MSC) — буквенно-цифровая классификационная система разделов математики и направлений математических исследований, разработанная и используемая двумя основными обзорными математическими базами данных — Mathematical Reviews и Zentralblatt MATH, ведомыми, соответственно, Американским математическим обществом и Европейским математическим обществом. Классификатор содержит более 5 тыс. сгруппированных в трёхуровневую иерархию элементов, каждый из которых отражает какую-либо специфическую тематику математических исследований.

Существует с 1940 года, приблизительно раз в десятилетие выходят корректировки. Используется многими математическими журналами, которые требуют от авторов указывать коды МПК в статьях в соответствии с тематикой.

Имеет трёхуровневую иерархическую структуру. Классификатор первого уровня — это две десятичные цифры, второго уровня — заглавная латинская буква, третьего уровня — две десятичные цифры. Например:

Классификатор должен содержать не менее двух цифр, например, 05 — комбинаторика.

Первый уровень[править | править код]

На первом уровне занумерованы свыше 40 основных разделов математики^[⇨]. Нумерация не сплошная, некоторые номера зарезервированы на будущее. Первые номера у разделов «Общее», «История и биографии», «Математическая логика и основания математики», «Комбинаторика», далее идёт серия алгебраических разделов, потом — различные разделы анализа, далее — разделы геометрии и топологии, чисто математическая часть верхнего уровня классификатора заканчивается следующими разделами: «Глобальный анализ, анализ на многообразиях» (связующим между топологией и анализом), «Теория вероятностей и случайные процессы», «Вычислительная математика». Начиная с кода 68 занумерованы прикладные категории — «Информатика», несколько разделов механики, физики, выделены разделы под астрономию, биологию, теорию систем и теорию управления. Последний код верхнего уровня классификации — 97, присвоен разделу «Математическое образование».

Второй уровень[править | править код]

На втором уровне латинскими буквами обозначены подразделы математических дисциплин занумерованных на первом уровне. Например, для дифференциальной геометрии (первый код 53) значения кодов второго уровня таковы:

• A — классическая дифференциальная геометрия,
• B — локальная дифференциальная геометрия,
• C — глобальная дифференциальная геометрия.

Помимо букв существует специальный код «-», который используется для специфических категорий:

• 53-00 — справочная информация (справочники, словари, библиографии)
• 53-01 — инструкции (учебники, руководства)
• 53-02 — обзорные материалы (монографии, обзоры)
• 53-03 — исторические материалы
• 53-04 — конкретные вычислительные процедуры и компьютерные программы
• 53-06 — труды, конференции и тому подобное.

Такие категории должны быть пятизначными.

Третий уровень[править | править код]

Код третьего уровня обозначает конкретную математическую проблему или объект. Например, 11P05 — проблема Варинга и её модификации.

Код третьего уровня 99 используется для обозначения всех проблем и объектов, которые не обозначены другими кодами.

Первая версия классификатора опубликована в 1940 году. В дальнейшем содержание классификатора уточнялось и выпускались новые версии, редакции вышли соответственно в 1959, 1973, 1980, 1985, 1991, 2000 и 2010 годах. Каждая редакция обозначается годом её принятия (например, MSC-2010 или МПК-2010), публикуются таблицы перехода с предыдущей версии классификатора на новую. Изменения проектируются таким образом, чтобы не возникало неоднозначностей, то есть, коды, занимаемые упраздняемыми элементами классификации, не используются новыми элементами, таким образом, возможен поиск по базам данных по устаревшим кодам классификаций. При крупных модификациях внутри раздела верхнего уровня он целиком переносился на новый код верхнего уровня, так, раздел «Логика и основания математики» при пересмотре в 1980 году перенесён с кода 02 в код 03, а «Теория чисел» в редакции 1985 года перенесена с кода 10 в код 11. Отдельные разделы верхнего уровня упразднялись и переназначались на второй уровень классификации в другую дисциплину, так, «Теория множеств» до 2000 года входила в классификацию на верхнем уровне с кодом 04, а начиная с МПК-2000 отнесена на второй уровень раздела «Математическая логика и основания математики» с кодом 03E. Для новых крупных направлений математических исследований при очередных пересмотрах назначались верхние уровни классификации, в частности, коды верхнего уровня получили «Многообразия и клеточные комплексы» (1959, код 57), «Глобальный анализ и анализ на многообразиях» (1973, код 58), «K-теория» (1985, код 19).

Текст классификатора редакции 2010 года распространяется под свободной лицензией (Creative Commons Attribution-Noncommercial-Share Alike).

• 00. Общее (англ. general)
• 01. История, биографии
• 03. Математическая логика и основания математики
• 05. Комбинаторика
• 06. Порядки, решётки, упорядоченные алгебраические структуры
• 08. Универсальная алгебра
• 11. Теория чисел
• 12. Теория полей, многочлены
• 13. Коммутативная алгебра
• 14. Алгебраическая геометрия
• 15. Линейная и полилинейная алгебра; теория матриц
• 16. Ассоциативные кольца и алгебры
• 17. Неассоциативные кольца и алгебры
• 18. Теория категорий, гомологическая алгебра
• 19. K-теория
• 20. Теория групп
• 22. Топологические группы, группы Ли
• 26. Вещественные функции
• 28. Мера и интегрирование
• 30. Функции комплексного переменного
• 31. Теория потенциала
• 32. Функции многих комплексных переменных и аналитические пространства^[en]
• 33. Специальные функции
• 34. Обыкновенные дифференциальные уравнения
• 35. Дифференциальные уравнения в частных производных
• 37. Динамические системы и эргодическая теория
• 39. Разностные и функциональные уравнения
• 40. Последовательности, ряды, суммируемость
• 41. Приближения и разложения
• 42. Гармонический анализ в евклидовых пространствах
• 43. Абстрактный гармонический анализ
• 44. Интегральные преобразования, операционное исчисление
• 45. Интегральные уравнения
• 46. Функциональный анализ
• 47. Теория операторов
• 49. Вариационное исчисление и оптимальное управление; оптимизация
• 51. Геометрия
• 52. Выпуклая и дискретная геометрия
• 53. Дифференциальная геометрия
• 54. Общая топология
• 55. Алгебраическая топология
• 57. Многообразия и клеточные комплексы
• 58. Глобальный анализ, анализ на многообразиях
• 60. Теория вероятностей и случайные процессы
• 62. Математическая статистика
• 65. Вычислительная математика (англ. numerical analysis
• 68. Информатика (англ. computer science)
• 70. Теоретическая механика (англ. mechanics of particles and systems)
• 74. Механика сплошных сред (англ. mechanics of deformable solids)
• 76. Механика жидкости (англ. fluid mechanics)
• 78. Оптика, теория электромагнетизма
• 80. Классическая термодинамика, теплопередача
• 81. Квантовая теория
• 82. Статистическая механика, строение вещества (англ. structure of matter)
• 83. Теория относительности и теория гравитации
• 85. Астрономия и астрофизика
• 86. Геофизика
• 90. Исследование операций, математическое программирование
• 91. Теория игр, экономика, общественные науки, «поведенческие науки» (англ. behavioral sciences)
• 92. Биология и другие естественные науки
• 93. Теория систем и управления
• 94. Информация и коммуникации, схемы (англ. circuits)
• 97. Математическое образование

• Mathematics Databases (by Timothy W. Cole) // Encyclopedia of Library and Information Science / M. Drake (editor). — N. Y.: Marcel Dekker, 2003. — С. 1792-1795. — ISBN 0-8247-2079-2.

Занимательная математика: 5 секретных приемов

Воспользуйтесь нашими советами, чтобы заинтересовать изучением математики даже тех, кто уверен, что ему с лихвой хватит знаний, полученных в начальной школе!

Среди школьников и их родителей бытует мнение, что есть ученики, которые легко понимают математику, и те, кому «не дано». Так ли это на самом деле? И, если так, что делать учителю, который в идеале обязан дотянуть каждого хотя бы до троечки?

Мы считаем, что понять и полюбить математику может каждый. Конечно, кому-то это сделать значительно легче, а от кого-то потребуется немало усилий. И вот тут без дополнительной мотивации не обойтись.

---

Давайте разберемся, как прорекламировать математику и пробудить интерес любого ученика.

Совет 1. Приведите интересные примеры из жизни.

Докажите, что математика — наука о реальной жизни, а не об абстрактных формулах, функциях и графиках. Хотите продемонстрировать наглядную связь математики, биологии и архитектуры? Расскажите ребятам о золотом сечении.

Правило золотого сечения проявляется во всем вокруг нас: начиная от структуры ДНК и заканчивая творениями древних архитекторов, художников и композиторов или современных кутюрье и фотографов.

Совет 2. Расскажите о великих математиках.

Докажите, что математика — это наука, которую создают и развивают неординарные личности. Чтобы прочувствовать гармонию и закономерность в числах, нужно быть необычным человеком.

Пифагор

Великий мудрец и философ, известный школьникам как автор теоремы, устанавливающей соотношение между сторонами прямоугольного треугольника, был незаурядной личностью. Обосновавшись в Кротоне (одной из греческих колоний в Южной Италии), Пифагор создал тайное общество, которое фактически пришло к власти.

Кстати, в 2014 году авторитетное издание Businessinsider составило список величайших уравнений и равенств, изменивших историю. Догадались, какое равенство заслуженно получило первое место? Конечно же, теорема Пифагора! 

 Алан Тьюринг

Жизнь этого математика — сюжет приключенческого фильма. Он раскодировал легендарную «Энигму» — шифровальную машину немецкой армии. Коды к ней менялись каждое утро, а алгоритм кодировки был не по зубам английским математикам, инженерам связи несколько лет. Алан Тьюринг не только разгадал секрет немецкого чуда шифровальной техники, но и создал первые прообразы современных компьютеров.

Ада Лавлейс

Дочь самого Байрона и величайший математик викторианской Англии. Она ввела понятия «цикл» и «рабочая ячейка», создала первые проекты вычислительных машин. Не зря эта дама носит почетный титул первого «программиста». 

Льюис Кэрролл

Этого детского писателя знают все. «Алиса в Стране чудес» и «Алиса в Зазеркалье» заняли достойное место среди шедевров мировой литературы. Но писатель в первую очередь был математиком. И даже преподавал 26 лет студентам линейную алгебру. 

Григорий Перельман

Именно он решил «загадку тысячелетия», доказав теорему Пуанкаре, но остается замкнутым и не любит шума вокруг своего имени. Великий математик отказался от Премии тысячелетия размером в миллион долларов, а позднее — и от Филдсовской премии, известной также как Нобелевская премия для математиков. 

 

Совет 3. Предложите ученикам прочитать увлекательные математические книги.

Прививать любовь и интерес к дисциплине необходимо не только на уроках.  Для этого воспользуйтесь подборкой тематических, развлекательных книг для школьников разного возраста. Уверены, эти произведения будут интересны самому широкому кругу читателей.

• Владимир Левшин «Новые рассказы рассеянного магистра». Автор умеет интересно в жанре приключенческой литературы описать разделы математики. Простота подачи информации, занимательный сюжет — за это произведения В. Левшина любят школьники и взрослые.
• Эвгения Кац «Необычная математика». Эта книга — реальный конкурент учебникам по математике для 1–2 класса. Интересные задачи не потребуют помощи родителей при их решении.
• А. Звонкина «Математика и малыши». Рекомендуем школьникам младших классов и их родителям. Пусть и взрослые поймут, что математика — не только арифметические действия со статичными цифрами.
• Яков Перельман «Занимательная арифметика». Автор популярной детской литературы воспитал любовь к математике не у одного поколения школьников.

• Леонард Млодинов «(Не)совершенная случайность. Как случай управляет нашей жизнью. Эта книга просто и доступно для всех, даже для гуманитариев,  объясняет теорию вероятности, показывает связь между точной дисциплиной и  естественными науками.
• Иэн Стюарт «Истина и красота. Всемирная история симметрии». О связи математики с точными науками знают все. Но влияние дисциплины ощутимо в архитектуре и мировых шедеврах. Заинтересовались? Тогда советуем прочитать книгу.
• Курант Р., Роббинс Г.  «Что такое математика?». Книга устраняет разрыв между сухим материалом школьных уроков математики и реальной жизнью, естественными науками.
• Н. Я. Виленкин «Функции в природе и технике». Автор подробно объясняет, как знания о функциях в реальной жизни помогают не только инженерам, но и людям самых разных профессий.

Совет 4. Расскажите ученикам о математических приложениях для смартфонов.

Они смогут играть и заниматься по ним дома или на перемене. Вы проявите себя как современного учителя, который не отстает от жизни и легко работает с современными гаджетами.

Для владельцев планшетов и смартфонов под управлением Android:

• «Математейка» поможет выучить таблицу умножения без зубрежки.
• «Математически игры» научат школьников быстро считать в уме. Для игроков предусмотрена система достижений, которая дополнительно мотивирует учеников к совершенствованию.
• «MalMath» — верный друг и помощник старшеклассника. Это приложение помогает решать задачи и подробно расписывает ход решения. Для самостоятельных и ответственных школьников «MalMath» может частично заменить репетитора по математике.
• «Пифагория» и «Пифагория 60°» заинтересуют школьников увлекательными геометрическим задачами на построение.
• «Euclidea» — это электронный сборник увлекательных интерактивных задач по геометрии. Авторы рекомендуют это приложение учителям, школьникам и всем любителям математики.

Для владельцев iPhone и iPad:

• «МатематУМ» научит школьников быстро и точно считать в уме. Регулярные занятия помогут улучшить внимательность и скорость мышления.
• «Math academy» — сборник увлекательных математических игр с приятным визуальным оформлением.
• «Правила математики» — это сборник правил, формул и теорем. Незаменимый помощник для тех, кто хочет изучить алгебру, геометрию, тригонометрию, элементы математического анализа, статистики и теории вероятности.
• «Мобильная математика» — это приложение, которым пользуются старшеклассники и студенты вузов. В приложении собраны основные формулы, а также представлены около 30 калькуляторов.
• «Пифагория», «Пифагория 60°» и «Euclidea» — это увлекательные сборники интерактивных геометрических задач на построение.

Совет 5. Участвуйте в наших конкурсах и олимпиадах по математике.

Задания наших образовательных мероприятий создают методисты с практическим опытом преподавания математики. В заданиях мы делаем упор на прикладной характер математических знаний и учитываем возрастные особенности школьников.

Организаторам дистанционных олимпиад и конкурсов мы дарим комплекты рабочих листов «Математика с Лантиком». Оцените качество наших рабочих листов прямо сейчас.

 

Скачать рабочие листы «Математика с Лантиком»

Скачайте рабочие листы, распечатайте их на цветном принтере и докажите, что математика — это весело и увлекательно. Ждем ваших учеников на наших образовательных мероприятиях!

 

Вам слово: 

С грамотным использованием интересных приемов даже математика станет понятной и увлекательной. Что вы используете для повышения интереса своих учеников к дисциплине?

 

Рекомендуем принять участие в мероприятих ЦРТ «Мега-Талант»

Понравилась статья?

Подпишитесь и мы будем присылать вам статьи на почту