Киматика что это такое – Звук как основа Мироздания. Часть первая. Как звук формирует нашу Реальность: mishawalk1 — LiveJournal — Школа №12 — Научно-образовательный центр школы №12 г. Челябинска

Содержание

Киматика — Википедия

Материал из Википедии — свободной энциклопедии

Киматика (от греч. κῦμα «волна») — физические эффекты звуковых волн, подмножество вибрационных модальных явлений. Эффектным и занимательным примером киматических явлений являются фигуры Хладни.
Название «киматика» (англ. cymatics, нем. kymatik) предложил Ханс Дженни (англ. Hans Jenny) в 1967 г.^[1]

Кроме того, киматикой (а также «киматической медициной», «киматической терапией» — англ. cymatic medicine, cymatic therapy) называют направление альтернативной медицины — созданную британским остеопатом Маннерсом (англ. P. G. Manners) «вибрационную биоэнергетическую медицину», в которой на тело человека воздействуют высокочастотным звуком^[2].

Первым киматические явления описал Роберт Гук, 8 июля 1680 года он увидел вызванные вибрацией узоры, когда двигал лук по краю стеклянной тарелки, покрытой мукой. На основе экспериментов Гука вибрационные узоры в XVIII веке изучал Эрнст Хладни, и такие узоры получили его имя (Фигуры Хладни)

[3].

В середине XX века фигуры Хладни изучал Ханс Дженни (англ. Hans Jenny) с помощью придуманного им устройства «тоноскоп» (англ. tonoscope). В 1967−72 г.г. Дженни издал двухтомник «Киматика» (англ. Cymatics: The Study of Wave Phenomena). Богато иллюстрированная книга многократно переиздавалась^[1].

В XXI веке распространилось основанное на принципах киматики духовное исцеление пением^[4].

Киматические эффекты используются при компенсации изгибных колебаний в пластинах со специальной структурой^[5].

Jenny, Hans. Cymatics : The Study of Wave Phenomena : Combined volumes One and Two : [англ.]. — Reprint ed. — Newmarket, NH : Macromedia Publishing, 2001.
Shapiro, Marcey. Transforming the Nature of Health : A Holistic Vision of Healing That Honors Our Connection to the Earth Others, and Ourselves : [англ.]. — North Atlantic Books, 2012. — xx+296[5] p. — ISBN 1583943617. — ISBN 978-1583943618.

Segen, Joseph C. The Dictionary of Alternative & Complementary Medicine : Subjective health care viewed with an objective eye : [англ.]. — BookBaby, 2010. — 500 p.

Память воды и сила звука

Киматика изучает свойства волн, этот термин был введён швейцарским учёным Хансом Йенни. Впервые учёный запечатлел на фотоплёнке воздействие звуковой волны на вещества разной природы — песок, вода, глина, рассыпанные на поверхности стальной пластины, под воздействием колебательных движений различной частоты принимали упорядоченный рисунок.

Киматика — наука о формообразующих свойствах волн.

Ханс Йенни продолжал работу немецкого учёного Эрнста Хладни (1756- 1827 гг.). Учёный проводил эксперименты воздействия звуковых волн на капли воды, и вновь и вновь приходил к выводу, что на неорганическую и органическую материю действуют одни и те же законы гармонической организации.

Гармоникаисты говорили, что «звук является космической тропой или лучами творения, диагональными к космическому источнику».

Мир цвета, звука и формы управляется по одним и тем же законам, и между гармониками и гармоническими структурами существуют тесные взаимосвязи. Гармоникаисты говорили, что звук является космической тропой или лучами творения, диагональными к космическому источнику.

В медитации свет и молчание становятся идентичными, творящими преобразующими.

Популярная теория происхождения Вселенной, поддерживаемая большинством теоретиков — теория «Большого взрыва». Согласно этой теории когда-то наша Вселенная представляла собой бесконечно малый сгусток, сверхплотный и раскаленный до очень высоких температур. Это нестабильное образование внезапно взорвалось, пространство быстро расширилось, а температура разлетающихся частиц, обладающих высокой энергией, начала снижаться. Взрыв был такой мощности, что световые и звуковые волны, возникшие в результате этого взрыва, преобразовывают свою энергию во всё новые и новые формы, при этом миллионы лет сотворяя мир в разных вариациях энергии звуковых и световых волн.

Числа и звуки

Исследования принципов, лежащих между музыкой и математикой, между звуком и числом со времён Пифагора, привлекало внимание учёных.

В двадцатых годах прошлого века немецкий учёный Ганс Кайзер разработал теорию мировых гармоник, возрождая забытую науку об обертонах (гармониках).

Кайзер исследовал закономерности, лежащие между звуком и числом.

Высота тона и длина струны находятся во взаимосвязи, — указывал Кайзер, то есть качество можно выводить из количества. Теория Кайзера утверждает, что принцип соотношение целых чисел является основой не только музыки, но и многих наук (химия, физика, астрономия, и др.). По мнению Кайзера, те формы в природе, в которых присутствуют гармонические соотношения в восприятии человека , считаются более красивыми. Соотношения, основанные на октаве (2:1), кварте (3:2), терции (5:4) отличаются особой соразмерностью.

Энергию Вселенной можно выразить октавой звукового спектра, октавой светового спектра, геометрической — иерархия форм кристаллов. Существует доказательная связь между частотами звука, цвета с геометрической формой. Наука, изучающая формы кристаллов и их внутреннего строения называется

кристаллография. Энергии проявленных форм существуют в тесном взаимодействии, преобразуясь друг в друге, эти энергии создают новые формы.

Форма и звуки

В научном исследовании д-ра Дженни, известном как “Киматика”, автор продемонстрировал геометрию звуковых вибраций, используя тонкие контейнеры, наполненные следующими средами: песком, спорами грибка Лигодеум, мокрым гипсом и разными формами жидкости, обладающими крошечными частицами или плавающими в них “коллоидами”.

В этой книге особый интерес представляет коллоидная жидкость. Находясь в состоянии покоя, коллоиды равномерно распределяются в жидкости, и вода становится мутной. Д-р Дженни называет такое состояние “гидродинамическим рассеиванием”.

Однако когда контейнер вибрировал на чистых диатонических звуках, частицы в жидкости собирались в упорядоченные и изолированные видимые геометрические паттерны, многие из которых обладали двумерной и трехмерной структурой. Иными словами, в них можно было наблюдать сформировавшуюся и ясно воспринимаемую глубину, то есть, они не были “плоскими “. В этой книге это одно из самых важных положений, которое следует изучить и помнить, ибо оно предоставляет неопровержимое визуальное доказательство концепций, которые мы обсуждали.

Есть пять основных трехмерных форм, и мы знаем их как Платоновы Тела, ибо честь их открытия принадлежит греческому философу Платону. Важно, чтобы было предельно ясно: наблюдая эти формы, на самом деле мы наблюдаем вибрацию. Сами формы могут не “существовать” как физический объект, а быть голограммой. Если вы попытаетесь их схватить или нарушить, они просто исчезнут и превратятся в рябь вокруг ваших пальцев. Тем не менее, не будучи нарушенными, формы будут существовать как очень реальная вибрация, и оказывать точно такое же давление на тело, которое вы ощущаете от очень громкого звука или раската грома.

Сейчас, когда мы увидели формы вибраций, работающие в жидкообразном эфире, мы знаем, что созданные их давлением силовые линии позволяют по-новому взглянуть на динамику гравитации. Имея неопровержимые свидетельства того, как эти геометрии формируют структурные особенности поверхности Земли, такие как континенты, подводные хребты и горные образования, нас больше не ослепит истина. И только дело времени, когда простые наблюдения превратятся в общеизвестное знание основной массы человечества.

Также, очень важно упомянуть следующее: когда студенты Фуллера повышали частоту в шаре, или Дженни повышал частоту в воде, старые формы растворялись и исчезали, а на их месте появлялась более сложная геометрическая форма. Такое явление работало и наоборот: когда частота понижалась до первоначального значения, вновь появлялись геометрии той же самой формы.

Поэтому, изучая динамику эфира, мы увидим: при повышении вибрационной частоты (или напряжения) энергии в данной области, сама геометрия этой области, например, формирующая Землю, будет спонтанно преобразовываться в более высокий порядок сложности. И эффекты повышения и понижения частоты происходят во всем Творении, включая все тела нашей Солнечной Системы, когда она двигается в Галактике.

Работа д-ра Спилхауса продемонстрировала, что со времени первичного “мега-континента” Пангеи, гравитационное поле Земли уже прошло через несколько подобных преобразований. В то время Земля имела единую кору. Это было до движения расширения, которое сейчас рассматривается в Теории Глобального Тектонического Расширения, созданной в 1933 году Отто Хильгенбергом.

Звук и энергия

Звук представляет собой поток энергии, текущей подобно водному потоку.

Звук может изменить среду, через которую он проходит, и сам изменяется ею. Каждая звуковая волна — есть сила, которая творит соответственную реакцию. Существует активная сила, воспринимающая сила и область их взаимодействий.

Согласные колебания образуют гармоничные частоты, что приводит к притяжению субатомных частиц друг к другу.

Диссонансные колебания вызывают разъединение или взрыв частицы или формы.

Американский учённый, живший в 19 веке, посвятил большую часть своей жизни изучению звука как силы, которая со временем стала служить в его экспериментах первичным импульсом для возбуждения таинственной энергии. Одним из величайших итогов творческой деятельности Джона Кили было открытие сорока Законов, управляющих вибрациями.

Эти законы явились фундаментом созданной им физики симпатических вибраций.

Данная область исследований, где Джон Кили был одиноким пионером, рассматривает внутреннюю природу вибрационных феноменов, основанную на симпатических, то есть резонансных взаимодействиях.

Ученый говорил, что звук это «нарушение атомного равновесия, разрушающее существующие атомные частицы, а освобожденная при этом субстанция, несомненно, должна быть эфирным током некоторого порядка». По его представлениям, все в Природе колеблется, вибрирует. Можно сказать, что в основе всей Природы лежат вибрации разных частот, которые создают разнообразнейшие сочетания. При этом «созвучные», гармоничные сочетания вызывают притяжение и носят созидательный характер, а дисгармоничные вызывают отталкивание, разрушают.

Пример организованных вибраций — музыка. Когда две струны музыкального инструмента настроены в гармоническом сочетании (например, в терцию, квинту, октаву), движение одной из них рождает отклик в другой.

А ведь с древнейших времен была известна и другая музыка, «музыка сфер», создаваемая Солнцем, Луной и планетами. Сегодня мы можем услышать эту музыку в компьютерном переложении, но, быть может, для древних посвященных она звучала намного богаче и ярче.

Кили назвал основанную им науку Sympathetic Vibratory Physics «физика симпатических (ответных) вибраций». Ему удалось не только объединить в этой науке фундаментальные физические понятия, но и выйти за рамки традиционной «физики», соединить ее с «метафизикой», с тем что лежит в области непознанного, в том числе и в духовной сфере.

Физика симпатических вибраций сведена в сорок законов, в которых постулированы, в частности, единство силы и материи, а также принципиальная бесконечность делимости последней. Для Кили сила есть освобожденная материя, а материя есть связанная сила, что блестяще подтвердилось в ХХ веке в виде известной даже школьнику формулы E=mc2. По расчетам Кили, энергии, содержащейся в ведре воды, вполне достаточно, чтобы сдвинуть наш мир с его курса.

К числу важнейших физических и метафизических категорий у Кили относится понятие нейтрального центра. Каждое проявленное тело во Вселенной от атома до звездной системы имеет в основании нейтральный центр, нерушимый фокус; вокруг него строится все, что мы осознаем в качестве материи, которая является его объективным проявлением.

«Сорок законов физики симпатических вибраций»

«Не существует разделения материи и силы на два различных понятия, поскольку они оба суть Едины. Сила есть освобожденная материя. Материя есть связанная сила.

Закон материи и силы.

В основе всей материи находится бесконечное и неизменное число атомолей, со-беспредельных с пространством и со-вечных с продолжительностью; они находятся в постоянном вибрационном движении, бесконечны в протяжении, неизменны в количестве и являются первоначалом всех форм энергии.

Закон вибрации тел.

Все когерентные агрегаты, изолированные от себе подобных тел, либо погруженные в среду, состоящую из материи в различных состояниях, вибрируют с установленным определённым тоном.

Закон колебания тел.

Все когерентные агрегаты, не изолированные от себе подобных тел, колеблются с периодом-частотой, которая гармонически соотносится с основным тоном вибрирующего тела; этот тон кратен тону атомоля.

Закон гармонических вибраций.

Все когерентные агрегаты постоянно вибрируют с периодом-частотой, которая гармонически соотносится с основным тоном вибрирующего тела; этот тон кратен тону атомоля.

Закон передачи вибрационной энергии.

Все колеблющиеся и вибрирующие когерентные агрегаты создают в среде, в которую они погружены, распространяющиеся вовне концентрические волны чередующихся сжатий и разрежений с периодом-частотой, равной тону агрегата.

Закон симпатических колебаний.

Любой когерентный агрегат, погруженный в среду, пульсирующую с частотой, равной собственной частоте агрегата, колеблется совместно со средой с той же частотой независимо от того, составляет ли тон среды унисон или какую-либо гармонику основного тона колеблющегося агрегата.

Закон притяжения.

Ближайшие когерентные агрегаты, вибрирующие в унисон или с гармоническим соотношением частот, взаимно притягиваются.

Закон отталкивания.

Ближайшие когерентные агрегаты, вибрирующие в диссонансе, взаимно отталкиваются.

Закон циклов.

Гармонически связанные когерентные агрегаты образуют центры вибраций, которые соотносятся с основным тоном, но не являются кратными к гармоникам, а вторичные соединения между ними порождают диссонансные тона независимо от того, являются ли они унисонами или обертонами к первоначальному тону. Так из гармонии рождается дисгармония, неизбежная причина бесконечных превращений.

Закон гармоник.

Любой агрегат в состоянии вибрации создаёт, дополнительно к своему основному тону, ряд вибраций из симметричных дробных долей самого себя, составляющих одно-, двух-, трёх- или многократное соотношение с основным тоном.

Закон силы. Энергия проявляет себя в трёх формах:

ПОРОЖДАЮЩЕЙ (вибрирующий агрегат),
ПЕРЕДАЮЩЕЙ (распространение изохронных волн в среде, в которую он погружен),
ПРИТЯГИВАЮЩЕЙ (его воздействие на другие агрегаты, способные вибрировать в унисон или гармонически с ним).

Закон колебания атомарной субстанции.

Когерентная атомарная субстанция способна колебаться с тоном, изменяющимся прямо пропорционально плотности и обратно пропорционально линейным размерам в пределах частот от одного периода в единицу времени (для 1-й октавы) вплоть до частоты 21-й октавы, создавая порождающую силу Звучания (Sonity), чья передающая сила (Звук) распространяется в твёрдых, жидких и газообразных средах, а её статическое воздействие (Звучность — Sonism) создаёт притяжение или отталкивание между симпатически вибрирующими телами в соответствии с Законом Гармонического Притяжения или Отталкивания.

Закон звукотеплотности.

Внутренние вибрации атомарных субстанций и атомарных молекул способны вибрировать с периодом-частотой, прямо пропорциональной их плотности, обратно пропорциональной их линейным размерам и прямо пропорциональной их целостности в пределах от 21-й до 42-й октавы. При этом создаётся порождающая сила Звукотеплотность (Sono-thermity), чья передающая сила Звукотеплота (Sono-therm) распространяется в твёрдых, жидких, газообразных и сверхгазообразных средах и статически создаёт сцепление и объединение молекул или их распад в соответствии с Законом Притяжения и Отталкивания.

Закон колебания атомов.

Все атомы в состоянии целостности (tension) способны колебаться с частотой, обратно пропорциональной кубу их атомных весов и прямо пропорциональной степени их целостности, в пределах от 42-й до 63-й октавы в секунду. При этом создаётся порождающая сила, Теплотность (Thermity), чья передающая сила, Рад-энергия (Radenergy)*, распространяется в твёрдом, жидком, газообразном эфире и производит статическое воздействие (Cohesion and Chemism — Сцепление и Химизм) на другие атомы, вызывая их соединение или распад в соответствии с Законом Гармонического Притяжения и Отталкивания.

Закон вибраций атомолярных субстанций.

Атомы способны вибрировать внутри себя с частотой, обратно пропорциональной Дину (локальному коэффициенту гравитации) и атомному объёму и прямо пропорциональной атомному весу. При этом создаётся порождающая сила (Электричество), чья передающая сила распространяется в атомолярных твёрдых, жидких, газообразных средах и создаёт индукционное и статическое магнитное воздействие на другие атомы, вызывая их притяжение или отталкивание в соответствии с Законом Гармонического Притяжения и Отталкивания.

Закон колебания атомолей.

Атомоли, колеблющиеся с одинаковым тоном (определяемым их одинаковыми размерами и весом), создают порождающую силу Атомоляцию (Atomolity), чья передающая форма, Гравизм, распространяется в более разряженной среде и производит статическое воздействие на все другие атомоли, именуемое Гравитацией (Gravity).

Закон преобразования сил.

Все силы являются различными формами Универсальной Энергии, которые отличаются своими периодами-частотами, переходящими друг в друга через неразличимые приращения; при этом каждая форма занимает диапазон в 21 октаву.

Каждую форму или тон можно преобразовать в эквивалентную высоту другого тона, расположенного выше или ниже на шкале из 105 октав. Данное преобразование может осуществляться только через статическое воздействие, развиваемое либо вибрациями гармонических тонов, выше и ниже их основного тона, либо близлежащими системами при сложении и вычитании их тонов, или каким-то третьим образом, в зависимости от конкретных условий.

Закон атомного тона.

Каждый атом имеет свой собственный определённый тон естественной вибрации. Закон изменения атомного тона посредством Рад-энергии. Высота тона высших гармоник и обертонов излучаемой

Рад-энергии достаточна для того, чтобы вызвать расширение атома; это же воздействие, побуждая атомоли непрерывно вибрировать, вызывает сжатие атома; таким образом, через изменение объёма меняется тон атома.

Закон изменения атомного тона посредством электричества и магнетизма.

Электричество и магнетизм порождают внутренние вибрации в атоме, которые сопровождаются пропорциональными изменениями его объёма, и, следовательно, тона.

Одной из ошибок современной науки является рассмотрение одних феноменов в изоляции от других, физика симпатических вибраций открывает нам бесконечность мироздания, в которой все предметы и явления — части Единого Целого.опубликовано econet.ru

Воздействие музыки на структуру воды. Опыты японских учёных.

О воздействии на воду простых слов и мыслей

Память воды. Привороты на воде. Запись эфира РЕН-ТВ.

Фрагмент документального фильма «Секретные истории: Закон мирового кодирования».
Телекомпания РЕН ТВ, передача была в эфире в декабре 2009 г.

P.S. И помните, всего лишь изменяя свое сознание — мы вместе изменяем мир! © econet

Сакральная геометрия — мандалы — киматика

Дельфин — разумное животное. Новые аргументы в пользу этой гипотезы дали недавние исследования ученых из Пенсильванского университета.

В течение достаточно длительного времени специалисты изучали язык дельфинов и получили поистине потрясающие результаты.

Как известно, звуковые сигналы возникают в носовом канале дельфинов в момент прохождения через него воздуха. Удалось установить, что животные используют шестьдесят базовых сигналов и пять уровней их комбинирования. Дельфины способны создавать «словарь» объемом 1012! Едва ли дельфины пользуются таким количеством «слов», но и объем их активного «вокабуляра» впечатляет — около 14 тысяч сигналов! Для сравнения: такое же количество слов составляет средний словарный запас человека.

А в повседневной жизни люди обходятся 800-1000 словами.

Сигнал дельфина, если перевести его на человеческий язык, представляет собой нечто вроде иероглифа, который означает больше, чем отдельное слово.

Наличие у дельфинов языка, по своей сложности превосходящего язык людей,

является настоящей сенсацией.

Редкие способности

Природа загадывает порой удивительные загадки. И одной из таких загадок, без сомнения, остаются дельфины. Несмотря на то что они обитают часто на виду у человека, знаем мы о них очень мало. Но даже то немногое, что известно об этих животных, поражает. Дельфины обладают поистине удивительными способностями. Настолько удивительными, что американец Джон Лилли, изучавший физиологию мозга в Пенсильванском университете, назвал дельфинов «параллельной цивилизацией».

Прежде всего ученых удивляют объем и строение дельфиньего мозга.

Исследователи из Пенсильванского университета поместили животное в чрево магнитно-резонансного томографа и увидели, что устройство нервной системы

у дельфинов столь совершенно, что порой кажется, будто она развита лучше, чем

у человека. «Головной мозг дельфина-афалины, — говорит профессор Лаела Саи, — весит 1700 граммов, это на 350 граммов больше, чем у взрослого мужчины.

По своей сложности мозг дельфина отнюдь не уступает мозгу человека: складок, бугорков и извилин в нем даже больше». Общее число нервных клеток у дельфина выше, чем у человека. Раньше ученые полагали, что мозг дельфина такой большой, потому что в нем нервные клетки размещены не столь плотно, как у людей.

Однако убедились в обратном: мозг в черепной коробке расположен одинаково.

Правда, внешне мозг дельфина больше похож на сферу, чем мозг homo sapiens,

который слегка приплюснут. У дельфинов существуют ассоциативные области коры, идентичные человеческим. «Этот факт косвенно указывает на то, что дельфины могут быть разумными», — считают специалисты по морской биологии.

Теменная, или двигательная, доля мозга дельфина превышает по своей площади теменную и лобную долю человека, вместе взятые. Почему природа так одарила

этих существ? Что это — результат многовековой эволюции или, может быть, «наследство» разумных предков?

Любопытно, что затылочные зрительные доли у дельфинов чрезвычайно велики,

а ведь они не особенно полагаются на зрение. Тогда для чего они им? Как известно, дельфины в большей степени «видят» ушами, испуская ультразвуки.

Акустическая линза на голове дельфина фокусирует ультразвук, направляя его

на различные объекты. Благодаря этому дельфин и «видит» ушами.

Он «ощупывает» подводный объект, определяя его форму.

— У обитателей морских глубин два органа слуха: один — обычный, другой — ультразвуковой, — рассказывает исследователь Марио Этти. — Внешний проход заращен, что повышает возможности слуха в воде. Рецепторы другого органа расположены по бокам нижней челюсти, ими воспринимаются малейшие звуковые колебания. Дельфин слышит своей нижней челюстью гораздо лучше, чем мы ушами. Слух дельфинов и косаток в 400-1000 раз острее человеческого. Благодаря множеству полостей в дыхале (носовом клапане) возникают акустические колебания, распространяющиеся на громадные расстояния в воде. Так, синие киты и кашалоты могут слышать звуки, издаваемые их собратьями за тысячи километров!

Как уже было сказано, дельфины виртуозно владеют своим речевым аппаратом. Продувая туда-обратно одну и ту же порцию воздуха, они рождают такую гамму звуков, что их вариации и количество намного превышают звуки, издаваемые человеком. При этом у каждого дельфина индивидуальный голос, свой темп и тембр речи, манера изъясняться и «почерк» мышления.

Весьма любопытно, что работающие одновременно органы слуха и речи создают удивительное богатство звуковой палитры. Возможности мозга млекопитающего так высоки, что он в состоянии проанализировать раздельно спектры, идущие с частотой 3000 импульсов в секунду! В этом случае временной интервал между импульсами составляет всего около 0,3 миллисекунды! И потому для дельфинов речь человека — очень медленный процесс. Они-то разговаривают в скоростном режиме. К тому же умеют вычленять в речи своих собратьев такие детали, о которых люди и не подозревают, так как наш с вами слух их уловить не может.

Но и это не все. Ученые провели серию экспериментов, доказывающих, что дельфины могут обмениваться весьма сложными сообщениями. Вот лишь один из примеров. Дельфину давали некое задание, которое должен был выполнить его собрат, находящийся в соседнем вольере. Через стенку вольера один дельфин «говорил» другому, что надо сделать. Например, взять красный треугольник и отдать человеку. Оба дельфина получали в награду по рыбешке. Однако было видно,

что работают они не за вознаграждение, их увлекал сам процесс творческого экспериментирования. Исследователи провели тысячи опытов, задания постоянно менялись, и ни разу дельфины не ошиблись. Единственно возможный вывод из этого: дельфины прекрасно понимают все происходящее и ориентируются в мире подобно людям.

Биологи, проводившие эксперименты, с удивлением замечали, что часто подопытные сами начинали управлять ходом эксперимента и его организаторами — людьми… Энергия творческого поиска передавалась дельфинам, и они предлагали экспериментаторам усложнить и модифицировать задание, при этом ученые неожиданно для себя замечали, что становятся экспериментальной моделью для дельфинов, которые пытались поменяться с ними ролями. Так кто кого изучал?

Киматика — узнай Правду о Вселенной!

Отличный материал и… с серьезной привязкой к колословам.
Как это может быть не покажется страным

Для обдумывания и изучения…
Ну просто очень в тему моих нынешних размышлений.
Дивлюсь как информация все время приходит ровно когда нужно, Слава Богам!

Оригинал взят у alex_alisauskas в Киматика — узнай Правду о Вселенной!

Киматика — это универсальный язык Вселенной

Послушайте… вы слышите…музыка…
Я слышу её везде… в порывах ветра… в воздухе…в лучах света…Она везде…
Всё, что нужно, просто открыться… Всё, что нужно, просто слушать…

Киматика

— это наука о формообразующих свойствах волн. Термин Киматика был введён учёным из Швейцарии Хансом Йенни, продолжившем работу немецкого учёного Эрнста Хладни (1756-1827 гг.). Воздействия звуковой волны на вещества разной природы Ханс Йенни запечатлел на отоплёнку. Он рассыпал на поверхность стальной пластины песок, глину, жидкие вещества и под воздействием колебательных движений разной частоты, вещества на пластине принимали упорядоченный рисунок. Сложность рисунка напрямую зависели от подаваемой звуковой частоты на пластину, чем выше частота, тем сложнее рисунок. Эти «звуковые орнаменты» впоследствии получили название Рисунки Хладни.

Швейцарец проводил эксперименты по воздействию звуковых волн на капли воды, и пришёл к выводу, что на органическую и неорганическую материю действуют одни и те же законы гармонической организации. Мир цвета и звука, формы управляется по одним и тем же законам, и между гармониками и гармоническими структурами существуют тесные взаимосвязи.
Дальше больше Киматика — это универсальный язык Вселенной

Этот фильм о волновой структуре пространства.
Он включает некоторые исторические и археологические факты, доказывающие структурированность пространства, а так же математическую модель, позволяющую понять волновую структуру пространства и строения вселенной.
Киматика Часть 1
Киматика — узнай Правду о Вселенной!

Киматика: evan_gcrm — LiveJournal

Оригинал взят у yamaha3

Киматика — это наука о формообразующих свойствах волн.

Термин Киматика был введён учёным из Швейцарии Хансом Йенни, продолжившем работу немецкого учёного Эрнста Хладни (1756-1827 гг.). Воздействия звуковой волны на вещества разной природы Ханс Йенни запечатлел на отоплёнку. Он рассыпал на поверхность стальной пластины песок, глину, жидкие вещества и под воздействием колебательных движений разной частоты, вещества на пластине принимали упорядоченный рисунок. Сложность рисунка напрямую зависели от подаваемой звуковой частоты на пластину, чем выше частота, тем сложнее рисунок. Эти «звуковые орнаменты» впоследствии получили название Рисунки Хладни.

В двадцатых годах прошлого века немецкий учёный Ганс Кайзер разработал теорию мировых гармоник возрождая забытую науку об обертонах (гармониках). Кайзер исследовал закономерности лежащие между звуком и числом Высота тона и длина струны находятся во взаимосвязи, то есть качество можно выводить из количества. Теория Кайзера (Пифагора) утверждает, что принцип соотношение целых чисел является основой не только музыки, но многих наук таких как химия, физика, астрономия, и др. По мнению Кайзера, те формы в природе в которых присутствуют гармонические соотношения в восприятии человека считаются более красивыми. Соотношения основанные на октаве (2:1), кварте (3:2), терции (5:4) отличаются особой соразмерностью.

Энергии Вселенной можно выразить октавой звукового спектра, октавой светового спектра, геометрической — иерархия форм кристаллов. Существует доказательная связь между частотами звука, цвета с геометрической формой, наука изучающая формы кристаллов и их внутреннего строения — называется кристаллография. Энергии проявленных форм существуют в тесном взаимодействии, преобразуясь в друг друге, эти энергии создают новые формы.

Форма и звуки

В научном исследовании д-ра Дженни, известном как “Киматика”, он продемонстрировал геометрию звуковых вибраций, используя тонкие контейнеры, наполненные следующими средами: песком, спорами грибка Лигодеум, мокрым гипсом и разными формами жидкости, обладающими крошечными частицами или плавающими в них “коллоидами”. В этой книге особый интерес представляет коллоидная жидкость. Находясь в состоянии покоя, коллоиды равномерно распределяются в жидкости, и вода становится мутной. Д-р Дженни называет такое состояние “гидродинамическим рассеиванием”. Однако когда контейнер вибрировал на чистых диатонических звуках, частицы в жидкости собирались в упорядоченные и изолированные видимые геометрические формы, из которых обладали двумерной и трёхмерной структурой. Иными словами, в них можно было наблюдать сформировавшуюся и ясно воспринимаемую глубину, то есть, они не были “плоскими“.

Звук и энергия

Звук представляет собой поток энергии, текущей подобно водному потоку. Звук может изменить среду, через которую он проходит, и сам изменяется ею. Каждая звуковая волна — есть сила, которая творит соответственную реакцию. Существует активная сила и воспринимающая сила и область их взаимодействий. Согласные колебания образуют гармоничные частоты, что приводит к притяжению субатомных частиц друг к другу. Диссонансные колебания вызывают разъединение или взрыв частицы или формы.

Математик — Википедия

Материал из Википедии — свободной энциклопедии

Матема́тик — учёный, специалист в области математики.

Профессия математика требует высшего университетского образования. Подготовка по математическим специальностям производится обычно в специальных учебных подразделениях университетов. В СССР это были математические или механико-математические, физико-математические факультеты^[1]. Дипломированные математики в СССР работали программистами, научными сотрудниками отраслевых институтов, преподавателями и т. д.^[2]

Наиболее престижной^{[источник не указан 91 день]} научной премией, вручаемой математикам, является Филдсовская премия. С 2002 года за выдающиеся достижения в области математики ежегодно вручается Абелевская премия. Нобелевские премии по математике не присуждаются, однако некоторым математикам (например, Л. В. Канторовичу или Дж. Ф. Нэшу) они присуждались (хотя и в других научных областях — часто экономике).

Несколько известных математиков написали автобиографии чтобы, среди прочего, рассказать публике, что заставило их посвятить жизнь этой науке. Эти произведения содержат замечательные рассказы о том, что значит быть математиком. Данный список содержит работы, некоторые из которых являются не автобиографиями а, скорее, эссе на тему математики и жизни математиков с автобиографическими элементами.

Один из самых знаменитых^{[источник не указан 91 день]} фильмов о математике — оскароносная биографическая драма «Игры разума» Рона Ховарда по одноимённой книге Сильвии Назар, рассказывающая о жизни Джона Форбса Нэша. Этот учёный прекрасно вписывается в стереотипное представление об учёном, как о мизантропе и его личность даёт повод начать разговор о связи гениальности и безумия^[3].

«Знаменитым математиком» обычно называет героя своих детских стихов и книг — академика Иванова — автор Эдуард Успенский. В 1986 году по книге режиссёром Владимиром Поповым на студии Союзмультфильм был снят мультфильм.^[4]

А. Н. Колмогоров. Математика — наука и профессия. — М.: Наука, 1988. — 288 с. — (Библиотечка квант). — 131 000 экз. — ISBN 5-02-013879-7.
С. Н. Левиева, В. С. Шнейдеров, Виктор Васильевич Шапкин. Мир профессий. Человек — знаковая система. — Молодая гвардия, 1988. — 352 с. — (Мир профессий).
Джордж Пойа. Математическое открытие. Решение задач: основные понятия, изучение и преподавание = Mathematical Discovery: On Understanding, Learning and Teaching Problem Solving. — М.: Наука, 1970. — 452 с. — 60 000 экз.
Герман Вейль. Математическое мышление. — М.: Наука, 1989. — 400 с.
Steven G. Krantz^[en]. A Mathematician comes of age. — The Mathematical Association of America, 2012. — ISBN 978-0-88385-578-2.
Jessica K. Sklar, Elizabeth S. Sklar. Mathematics in Popular Culture: Essays on Appearances in Film, Fiction, Games, Television and Other Media. — McFarland, 2012. — 353 с. — ISBN 978-0-7864-4978-1.
Burkard Polster, Marty Ross. Math Goes to the Movies. — JHU Press^[en], 2012. — 304 с. — ISBN 978-1-4214-0484-4.
Математика // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Математический анализ — Википедия

Эта статья — о математическом анализе в классическом понимании — разделе, объединяющем дифференциальное и интегральное исчисления. Об исторических аспектах его возникновения см. Анализ бесконечно малых; о математическом анализе в широком смысле, как современном направлении в математике см. Анализ (раздел математики).

Математи́ческий ана́лиз (классический математический анализ) — совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно малых», объединяет дифференциальное^[⇨] и интегральное^[⇨] исчисления.

На классическом математическом анализе основывается современный анализ, который рассматривается как одно из трёх основных направлений математики (наряду с алгеброй и геометрией). При этом термин «математический анализ» в классическом понимании используется, в основном, в учебных программах и материалах^[1]. В англо-американской традиции классическому математическому анализу соответствуют программы курсов с наименованием «исчисление» (англ. Calculus).

Предшественниками математического анализа были античный метод исчерпывания и метод неделимых. Все три направления, включая анализ, роднит общая исходная идея: разложение на бесконечно малые элементы, природа которых, впрочем, представлялась авторам идеи довольно туманной. Алгебраический подход (исчисление бесконечно малых) начинает появляться у Валлиса, Джеймса Грегори и Барроу. В полной мере новое исчисление как систему создал Ньютон, который, однако, долгое время не публиковал свои открытия^[2].

Официальной датой рождения дифференциального исчисления можно считать май 1684 года, когда Лейбниц опубликовал первую статью «Новый метод максимумов и минимумов…»^[3]. Эта статья в сжатой и малодоступной форме излагала принципы нового метода, названного дифференциальным исчислением.

Лейбниц и его ученики[править | править код]

Готфрид Вильгельм Лейбниц

В конце XVII века вокруг Лейбница возникает кружок, виднейшими представителями которого были братья Бернулли (Якоб и Иоганн) и Лопиталь. В 1696, используя лекции И. Бернулли, Лопиталь написал первый учебник^[4], излагавший новый метод в применении к теории плоских кривых. Он назвал его Анализ бесконечно малых, дав тем самым и одно из названий новому разделу математики. В основу изложения положено понятие переменных величин, между которыми имеется некоторая связь, из-за которой изменение одной влечёт изменение другой. У Лопиталя эта связь даётся при помощи плоских кривых: если M{\displaystyle M} — подвижная точка плоской кривой, то её декартовы координаты x{\displaystyle x} и y{\displaystyle y}, именуемые абсциссой и ординатой кривой, суть переменные, причём изменение x{\displaystyle x} влечёт изменение y{\displaystyle y}. Понятие функции отсутствует: желая сказать, что зависимость переменных задана, Лопиталь говорит, что «известна природа кривой». Понятие дифференциала вводится так:

Бесконечно малая часть, на которую непрерывно увеличивается или уменьшается переменная величина, называется её дифференциалом… Для обозначения дифференциала переменной величины, которая сама выражается одной буквой, мы будем пользоваться знаком или символом d{\displaystyle d}.^[5] … Бесконечно малая часть, на которую непрерывно увеличивается или уменьшается дифференциал переменной величины, называется … вторым дифференциалом.^[6]

Эти определения поясняются геометрически, при этом на рис. бесконечно малые приращения изображены конечными. Рассмотрение опирается на два требования (аксиомы). Первое:

Требуется, чтобы две величины, отличающиеся друг от друга лишь на бесконечно малую величину, можно было брать [при упрощении выражений?] безразлично одну вместо другой.^[7]

Отсюда получается x+dx=x{\displaystyle x+dx=x}, далее

dxy=(x+dx)(y+dy)−xy=xdy+ydx+dxdy=(x+dx)dy+ydx=xdy+ydx{\displaystyle dxy=(x+dx)(y+dy)-xy=xdy+ydx+dxdy=(x+dx)dy+ydx=xdy+ydx}

и проч. правила дифференцирования.

Касательная к кривой

Второе требование гласит:

Требуется, чтобы можно было рассматривать кривую линию как совокупность бесконечного множества бесконечно малых прямых линий.^[8]

Продолжение каждой такой линии называется касательной к кривой.^[9] Исследуя касательную, проходящую через точку M=(x,y){\displaystyle M=(x,y)}, Лопиталь придаёт большое значение величине

ydxdy−x{\displaystyle y{\frac {dx}{dy}}-x},

достигающее экстремальных значений в точках перегиба кривой, отношению же dy{\displaystyle dy} к dx{\displaystyle dx} не придаётся никакого особого значения.

Примечательно нахождение точек экстремума. Если при непрерывном увеличении абсциссы x{\displaystyle x} ордината y{\displaystyle y} сначала возрастает, а затем убывает, то дифференциал dy{\displaystyle dy} сначала положителен по сравнению с dx{\displaystyle dx}, а потом отрицателен.

Но всякая непрерывно возрастающая или убывающая величина не может превратиться из положительной в отрицательную, не проходя через бесконечность или нуль… Отсюда следует, что дифференциал наибольшей и наименьшей величины должен равняться нулю или бесконечности.^[10]

Вероятно, эта формулировка небезупречна, если вспомнить о первом требовании: пусть, скажем, y=x2{\displaystyle y=x^{2}}, тогда в силу первого требования

2xdx+dx2=2xdx{\displaystyle 2xdx+dx^{2}=2xdx};

в нуле правая часть равна нулю, а левая нет. Видимо следовало сказать, что dy{\displaystyle dy} можно преобразовать в соответствии с первым требованием так, чтобы в точке максимума dy=0{\displaystyle dy=0}.^[11] В примерах все само собой понятно, и лишь в теории точек перегиба Лопиталь пишет, что dy{\displaystyle dy} равен нулю в точке максимума, будучи разделён на dx{\displaystyle dx}^[10].

Далее, при помощи одних дифференциалов формулируются условия экстремума и рассмотрено большое число сложных задач, относящихся в основном к дифференциальной геометрии на плоскости. В конце книги, в гл. 10, изложено то, что теперь называют правилом Лопиталя, хотя и в не совсем обычной форме. Пусть величина ординаты y{\displaystyle y} кривой выражена дробью, числитель и знаменатель которой обращаются в нуль при x=a{\displaystyle x=a}. Тогда точка кривой с x=a{\displaystyle x=a} имеет ординату y{\displaystyle y}, равную отношению дифференциала числителя к дифференциалу знаменателя, взятому при x=a{\displaystyle x=a}.

По замыслу Лопиталя написанное им составляло первую часть Анализа, вторая же должна была содержать интегральное исчисление, то есть способ отыскания связи переменных по известной связи их дифференциалов. Первое его изложение дано Иоганном Бернулли в его Математических лекциях о методе интеграла^[12]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка.

Указывая на практическую полезность и простоту нового метода Лейбниц писал:

То, что человек, сведущий в этом исчислении, может получить прямо в трёх строках, другие учёнейшие мужи принуждены были искать, следуя сложными обходными путями.

Эйлер[править | править код]

Леонард Эйлер

Перемены, произошедшие за последующие полвека, отражены в обширном трактате Эйлера. Изложение анализа открывает двухтомное «Введение», где собраны изыскания о различных представлениях элементарных функций. Термин «функция» впервые появляется лишь в 1692 у Лейбница,^[13] однако на первые роли его выдвинул именно Эйлер. Изначальная трактовка понятия функции состояла в том, что функция — это выражение для счёта (нем. Rechnungsausdrϋck) или аналитическое выражение.^[14]

Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств.^[15]

Подчёркивая, что «основное различие функций лежит в способе составления их из переменного и постоянных», Эйлер перечисляет действия, «посредством которых количества могут друг с другом сочетаться и перемешиваться; действиями этими являются: сложение и вычитание, умножение и деление, возведение в степень и извлечение корней; сюда же следует отнести также решение [алгебраических] уравнений. Кроме этих действий, называемых алгебраическими, существует много других, трансцендентных, как то: показательные, логарифмические и бесчисленные другие, доставляемые интегральным исчислением».^[16] Такая трактовка позволяла без труда обращаться с многозначными функциями и не требовала пояснения, над каким полем рассматривается функция: выражение для счёта определено для комплексных значений переменных даже тогда, когда для рассматриваемой задачи это не нужно.

Операции в выражении допускались лишь в конечном числе, а трансцендентное проникало при помощи бесконечно большого числа ∞{\displaystyle \infty }^[17]. В выражениях это число используется наряду с натуральными числами. Напр., считается допустимым такое выражение для экспоненты

ex=(1+x∞)∞{\displaystyle e^{x}=\left(1+{\frac {x}{\infty }}\right)^{\infty }},

в котором лишь поздние авторы видели предельный переход. С аналитическими выражениями производились разнообразные преобразования, позволившие Эйлеру найти представления для элементарных функций в виде рядов, бесконечных произведений и т. д. Эйлер преобразует выражения для счёта так, как это делают в алгебре, не обращая внимания на возможность вычислить значение функции в точке по каждой из написанных формул.

В отличие от Лопиталя Эйлер подробно рассматривает трансцендентные функции и в особенности два наиболее изученных их класса — показательные и тригонометрические. Он обнаруживает, что все элементарные функции могут быть выражены при помощи арифметических действий и двух операций — взятия логарифма и экспоненты^[18].

Сам ход доказательства прекрасно демонстрирует технику использования бесконечно большого. Определив синус и косинус при помощи тригонометрического круга, Эйлер выводит из формул сложения следующее:

(cos⁡x+−1sin⁡x)(cos⁡y+−1sin⁡y)=cos⁡(x+y)+−1sin⁡(x+y),{\displaystyle (\cos x+{\sqrt {-1}}\sin x)(\cos y+{\sqrt {-1}}\sin y)=\cos {(x+y)}+{\sqrt {-1}}\sin {(x+y)},}

а отсюда

2cos⁡nx=(cos⁡x+−1sin⁡x)n+(cos⁡x−−1sin⁡x)n{\displaystyle 2\cos nx=(\cos x+{\sqrt {-1}}\sin x)^{n}+(\cos x-{\sqrt {-1}}\sin x)^{n}}

Полагая n=∞{\displaystyle n=\infty } и z=nx{\displaystyle z=nx}, он получает

2cos⁡z=(1+−1z∞)∞+(1−−1z∞)∞=e−1z+e−−1z{\displaystyle 2\cos z=\left(1+{\frac {{\sqrt {-1}}z}{\infty }}\right)^{\infty }+\left(1-{\frac {{\sqrt {-1}}z}{\infty }}\right)^{\infty }=e^{{\sqrt {-1}}z}+e^{-{\sqrt {-1}}z}},

отбрасывая бесконечно малые величины большего порядка. Используя это и аналогичное выражение, Эйлер получает и свою знаменитую формулу

e−1x=cos⁡x+−1sin⁡x{\displaystyle e^{{\sqrt {-1}}x}=\cos {x}+{\sqrt {-1}}\sin {x}}.

Указав различные выражения для функций, которые теперь называют элементарными, Эйлер переходит к рассмотрению кривых на плоскости, начертанным свободным движением руки. По его мнению, не для всякой такой кривой можно отыскать единое аналитическое выражение (см. также Спор о струне).^[19] В XIX веке с подачи Казорати^[20] это утверждение считалось ошибочным: по теореме Вейерштрасса всякая непрерывная в современном смысле кривая может быть приближенно описана полиномами. На самом деле Эйлера это едва ли убедило, ведь нужно ещё переписать предельный переход при помощи символа ∞{\displaystyle \infty }.

Изложение дифференциального исчисления Эйлер начинает с теории конечных разностей, за ним в третьей главе следует философское разъяснение о том, что «бесконечно малое количество есть точно нуль», более всего не устроившее современников Эйлера. Затем из конечных разностей при бесконечно малом приращении образуются дифференциалы, а из интерполяционной формулы Ньютона — формула Тейлора. Этот метод в существенном восходит к работам Тейлора (1715 г.). При этом у Эйлера появляется устойчивое отношение dkydxk{\displaystyle {\frac {d^{k}y}{dx^{k}}}}, которое, однако, рассматривается как отношение двух бесконечно малых. Последние главы посвящены приближенному вычислению при помощи рядов.

В трёхтомном интегральном исчислении Эйлер вводит понятие интеграла так:

Та функция, дифференциал которой =Xdx{\displaystyle =Xdx}, называется его интегралом и обозначается знаком S{\displaystyle S}, поставленным спереди.^[21]

В целом же эта часть трактата Эйлера посвящена более общей с современной точки зрения задаче об интегрировании дифференциальных уравнений. При этом Эйлер находит ряд интегралов и дифференциальных уравнений, которые приводят к новым функциям, напр., Γ{\displaystyle \Gamma }-функции, эллиптические функции и т. д. Строгое доказательство их неэлементарности было дано в 1830-х годах Якоби для эллиптических функций и Лиувиллем (см. элементарные функции).

Лагранж[править | править код]

Следующим крупным произведением, сыгравшим значительную роль в развитии концепции анализа, явилась Теория аналитических функций^[22]Лагранжа и обширный пересказ работ Лагранжа, выполненный Лакруа^[23] в несколько эклектической манере.

Желая избавиться от бесконечно малого вовсе, Лагранж обратил связь между производными и рядом Тейлора. Под аналитической функцией Лагранж понимал произвольную функцию, исследуемую методами анализа. Саму функцию он обозначил как f(x){\displaystyle f(x)}, дав графический способ записи зависимости — ранее же Эйлер обходился одними переменными. Для применения методов анализа по мнению Лагранжа необходимо, чтобы функция разлагалась в ряд

f(x+h)=f(x)+ph+qh3+…{\displaystyle f(x+h)=f(x)+ph+qh^{2}+\dots },

коэффициенты которого будут новыми функциями x{\displaystyle x}. Остаётся назвать p{\displaystyle p} производной (дифференциальным коэффициентом) и обозначить его как f′(x){\displaystyle f'(x)}. Таким образом, понятие производной вводится на второй странице трактата и без помощи бесконечно малых. Остаётся заметить, что

f′(x+h)=p+2qh+…{\displaystyle f'(x+h)=p+2qh+\dots },

поэтому коэффициент q{\displaystyle q} является удвоенной производной производной f(x){\displaystyle f(x)}, то есть

q=12!f″(x){\displaystyle q={\frac {1}{2!}}f»(x)} и т. д.^[24]

Такой подход к трактовке понятия производной используется в современной алгебре и послужил основой для создания теории аналитических функций Вейерштрасса.

Лагранж оперировал такими рядами как формальными и получил ряд замечательных теорем. В частности, впервые и вполне строго доказал разрешимость начальной задачи для обыкновенных дифференциальных уравнений в формальных степенных рядах.^[25]

Вопрос об оценке точности приближений, доставляемых частными суммами ряда Тейлора, впервые был поставлен именно Лагранжем: в конце Теории аналитических функций он вывел то, что теперь называют формулой Тейлора с остаточным членом в форме Лагранжа.^[26] Однако, в противоположность современным авторам, Лагранж не видел нужды в употреблении этого результата для обоснования сходимости ряда Тейлора.

Вопрос о том, действительно ли функции, употребимые в анализе, могут быть разложены в степенной ряд, впоследствии стал предметом дискуссии. Конечно, Лагранжу было известно, что в некоторых точках элементарные функции могут не разлагаться в степенной ряд, однако в этих точках они и недифференцируемы ни в каком смысле. Коши в своём Алгебраическом анализе привёл в качестве контрпримера функцию

f(x)=e−1/x2,{\displaystyle f(x)=e^{-1/x^{2}},}

доопределённую нулём в нуле. Эта функция всюду гладкая на вещественной оси и в нуле имеет нулевой ряд Маклорена, который, следовательно, не сходится к значению f(x){\displaystyle f(x)}. Против этого примера Пуассон возразил, что Лагранж определял функцию как единое аналитическое выражение, в примере Коши же функция задана по-разному в нуле, и при x≠0{\displaystyle x\not =0}. Лишь в конце XIX века Прингсхайм^[27] доказал, что существует бесконечно дифференцируемая функция, заданная единым выражением, ряд Маклорена для которой расходится. Пример такой функции представляет выражение

Ψ(x)=∑k=0∞cos⁡(3kx)k!{\displaystyle \Psi (x)=\sum \limits _{k=0}^{\infty }{\frac {\cos {(3^{k}x)}}{k!}}}.

Дальнейшее развитие[править | править код]

В XVIII веке были на основе классического анализа разработаны и практически применены такие новые ветви, как вариационное исчисление, обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных, преобразования Фурье и производящие функции. На фундаменте анализа возникла математическая физика, аналитические методы глубоко проникли в геометрию и даже в теорию чисел.

В XIX веке Коши первым дал анализу твёрдое логическое обоснование, введя понятие предела последовательности, он же открыл новую страницу комплексного анализа. Пуассон, Лиувилль, Фурье и другие изучали дифференциальные уравнения в частных производных и гармонический анализ.

В последней трети XIX века Вейерштрасс произвёл арифметизацию анализа, полагая геометрическое обоснование недостаточным, и предложил классическое определение предела через (ε,δ){\displaystyle (\varepsilon ,\delta )}-язык^[en]. Он же создал первую строгую теорию множества вещественных чисел. В это же время попытки усовершенствования теоремы об интегрируемости по Риману привели к созданию классификации разрывности вещественных функций. Также были открыты «патологические» примеры (нигде не дифференцируемые непрерывные функции, заполняющие пространство кривые). В связи с этим Жордан разработал теорию меры, а Кантор — теорию множеств, и в начале XX века математический анализ был формализован с их помощью. Другим важным событием XX века стала разработка Робинсоном нестандартного анализа — альтернативного подхода к обоснованию анализа; притом средствами нестандартного анализа обнаружены несколько новых результатов, которые не были известны в классическом анализе, но принципиально могли бы быть получены и классическими средствами^[28].

$(\varepsilon, \delta)$

Касательная в точке (x, f(x)). Производная f′(x) кривой в точке равна наклону касательной к этой кривой в данной точке.

Дифференциальное исчисление изучает определение, свойства и применение производных функций. Процесс нахождения производной называется дифференцированием. Для заданной функции и точки из области её определения производная в этой точке является способом кодирования мелкомасштабного поведения этой функции вблизи этой точки. Найдя производную функции в каждой точке в области определения, можно определить новую функцию, называемую производной функцией или просто производной от исходной функции. На математическом языке производная является линейным отображением, на входе которого одна функция, а на выходе другая. Это понятие является более абстрактным, чем большинство процессов, изучаемых в элементарной алгебре, где функции обычно имеют на входе одно число, а на выходе другое. Например, если для функции удвоения задать на входе три, на выходе будет шесть; если для квадратичной функции задать на входе три, на выходе будет девять. Производная же может иметь квадратичную функцию в качестве входа. Это означает, что производная берёт всю информацию о функции возведения в квадрат, то есть: при входе два, она даёт на выходе четыре, три преобразует в девять, четыре — в шестнадцать и так далее, и использует эту информацию для получения другой функции. (Производной квадратичной функции является как раз функция удвоения.)

Наиболее распространенным символом для обозначения производной является апострофо-подобный знак, называемый штрихом. Таким образом, производная функции f есть f′, произносится «f штрих». Например, если f(x) = x² является функцией возведения в квадрат, то f′(x) = 2x является её производной, это функция удвоения.

Если входом функции является время, то производная представляет собой изменение по времени. Например, если f является функцией, зависящей от времени, и она даёт на выходе положение мяча во времени, то производная f определяет изменение положения мяча по времени, то есть скорость мяча.

Если функция является линейной (то есть, если графиком функции является прямая линия), то функцию можно записать в виде y = mx + b, где x — независимая переменная, y — зависимая переменная, а b — это y-отсечка, при этом:

m=riserun=change in ychange in x=ΔyΔx.{\displaystyle m={\frac {\text{rise}}{\text{run}}}={\frac {{\text{change in }}y}{{\text{change in }}x}}={\frac {\Delta y}{\Delta x}}.}

Это выражение даёт точное значение угла наклона прямой линии. Если график функции не является прямой линией, то изменение y делённое на изменение x меняется от точки к точке. Производная даёт точный смысл понятия изменения выходного значения по отношению к изменению входа. Чтобы быть конкретным, пусть f есть функция, и мы фиксируем точку a в области определения f. (a, f(a)) является точкой на графике функции. Если h — близкое к нулю число, то a + h является числом, близким к a. Поэтому точка (a + h, f(a + h)) близка к точке (a, f(a)). Угол наклона между этими двумя точками равен:

m=f(a+h)−f(a)(a+h)−a=f(a+h)−f(a)h.{\displaystyle m={\frac {f(a+h)-f(a)}{(a+h)-a}}={\frac {f(a+h)-f(a)}{h}}.}

Это выражение называется разностным соотношением. Линия, проходящая через две точки на кривой, называется секущей линией, поэтому m является углом наклона секущей линии между (a, f(a)) и (a + h, f(a + h)). Секущая является лишь приближением к поведению функции в точке, поскольку она не учитывает поведение функции между точками a и (a + h, f(a + h)). Определить это поведении, установив h равным нулю, невозможно, поскольку потребовалось бы делить на ноль, что исключено. Производная определяется путём перехода к пределу при h стремящемся к нулю, что означает, что он рассматривает поведение f для всех малых значениях h и выделяет приемлемое значение для случая, когда h равно нулю:

limh→0f(a+h)−f(a)h.{\displaystyle \lim _{h\to 0}{f(a+h)-f(a) \over {h}}.}

Геометрически производная равна углу наклона касательной к графику функции f в точке a. Касательная является пределом секущих линий, так же как производная является пределом разностных соотношений. По этой причине производную иногда называют наклоном функции f.

Вот конкретный пример, производная функция возведения в квадрат в точке 3. Пусть f(x) = x² является квадратичной функцией.

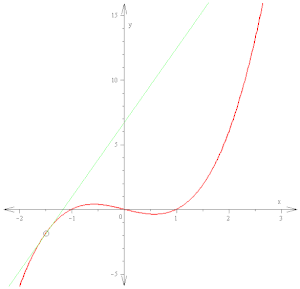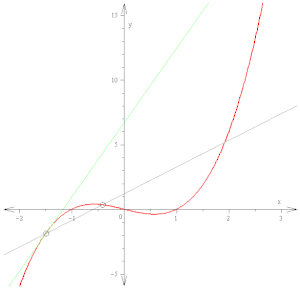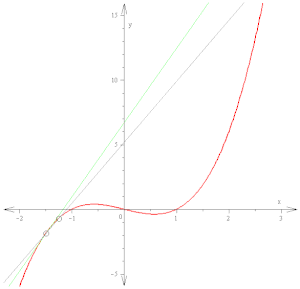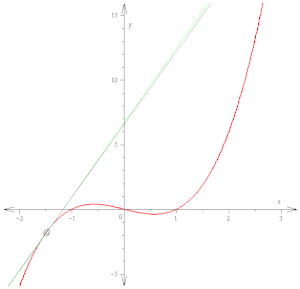$\lim_{h \to 0}{f(a+h) - f(a)\over{h}}.$ Производная f′(x) кривой в точке есть наклон касательной к этой кривой в данной точке. Этот наклон определяется путём нахождения предельной величины наклона секущих. Здесь используется функция f(x) = x³ − x (изображена красным цветом). Касательная (зелёный цвет), которая проходит через точку (-3/2, −15/8), имеет наклон 23/4. Обратите внимание, что вертикальный и горизонтальный масштаб в этом изображении разные.

f′(3)=limh→0(3+h)2−32h=limh→09+6h+h3−9h=limh→06h+h3h=limh→0(6+h)=6.{\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6.\end{aligned}}}

Наклон касательной к квадратичной функции в точке (3;9) равно 6, то есть она растёт вверх в шесть раз быстрее, чем отклоняется право. Вычисление предела, описанное выше, можно выполнить для любой точки в области определения квадратичной функции. Это определяет производную функцию или просто для краткости производную от функции возведения в квадрат. Проведённые расчёты показывают что производная квадратичной функции есть функция удвоения.

Интегральное исчисление — это изучение определения, свойств и применения двух взаимосвязанных понятий: неопределённого интеграла и определённого интеграла. Процесс поиска значения интеграла называется интегрированием. В технических терминах интегральное исчисление является исследованием двух связанных линейных операторов.

Неопределённый интеграл является первообразной, то есть операцией, обратной к производной. F является неопределённым интегралом от f в том случае, когда f является производной от F. (Это использование прописных и строчных букв для функции и её неопределённого интеграла распространено в исчислении).

Определенный интеграл входной функции и выходных значений есть число, которое равно площади поверхности, ограниченной графиком функции, осью абсцисс и двумя отрезками прямых линий от графика функции до оси абсцисс в точках выходных значений. В технических терминах определённый интеграл есть предел суммы площадей прямоугольников, называемой суммой Римана.

Примером из физики является вычисление пройденного расстояния при ходьбе в любой момент времени.

Distance=Speed⋅Time{\displaystyle \mathrm {Distance} =\mathrm {Speed} \cdot \mathrm {Time} }

Если скорость постоянна, достаточно операции умножения, но если скорость меняется, то мы должны применить более мощный метод вычисления расстояния. Одним из таких методов является приблизительное вычисление путём разбивки времени на отдельные короткие промежутки. Умножая затем время в каждом интервале на какую-либо одну из скоростей в этом интервале и затем суммируя все приблизительные расстояния (сумма Римана), пройденные в каждом интервале, мы получим полное пройденное расстояние. Основная идея состоит в том, что если использовать очень короткие интервалы, то скорость на каждом из них будет оставаться более или менее постоянной. Тем не менее, сумма Римана даёт только приблизительное расстояние. Чтобы найти точное расстояние, мы должны найти предел всех таких сумм Римана.

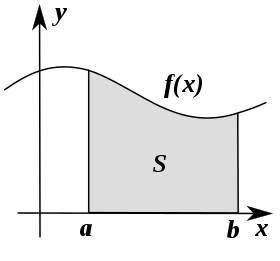$\mathrm{Distance} = \mathrm{Speed} \cdot \mathrm{Time}$

Интегрирование можно рассматривать как вычисление площади под кривой, определённой уравнением f(x), между двумя точками (здесь a и b).

Если f(x) на диаграмме слева представляет изменение скорости с течением времени, то пройденное расстояние (между моментами a и b) есть площадь заштрихованной области s.

Для приближённой оценки этой площади возможен интуитивный метод, состоящий в