Таблица умножения на 6, 7, 8 и 9 на пальцах
Если моя память мне не изменяет, таблица умножения до 5 включительно далась достаточно легко. Но вот с умножением на 6, 7, 8 и 9 возникали определенные трудности. Если бы я знала такой трюк раньше, домашнее задание выполнялось бы минимум в два раза быстрее 😉
©photo
Умножение на 6, 7 и 8
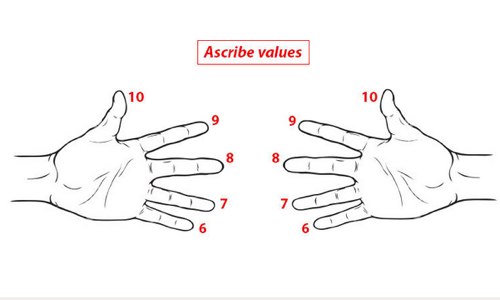таблица умножения на пальцахПоверните кисти ладонями к себе и присвойте каждому пальцу цифры от 6 и до 10 начиная с мизинца.
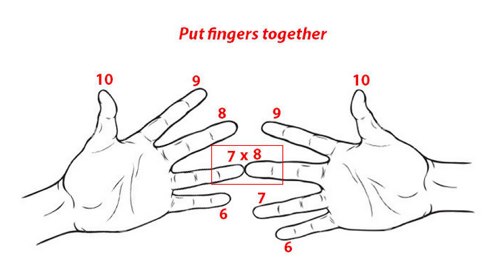
Теперь попробуем умножить, например, 7х8. Для этого соедините палец №7 на левой руке с пальцем №8 на правой.
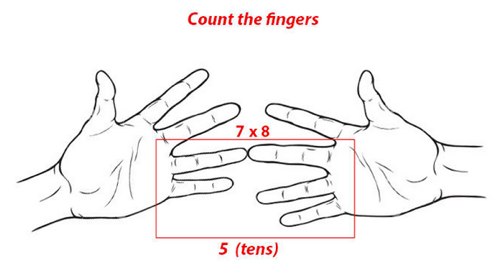
А теперь считаем пальцы: количество пальцев под соединенными — это десятки.
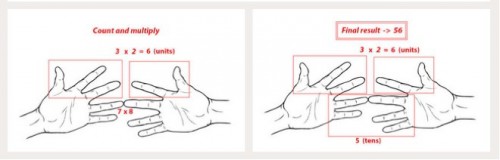таблица умножения на пальцах(картинка кликабельна)
А пальцы левой руки, оставшиеся сверху, умножаем на пальцы правой — это и будут наши единицы (3х2=6). Итоге равен 56.
Иногда бывает так, что при умножении «единиц» результат получается больше 9. В таких случаях нужно плюсовать оба результата в столбик.
Например, 7х6. В этом случае получается, что «единицы» равны 12 (3х4). В десятки равны 3.
3 (десятки)
+
12 (единицы)
________
42
Умножение на 9
Снова поверните кисти ладонями к себе, но теперь нумерация пальцев будет идти по порядку с лева на право, то есть от 1 до 10.
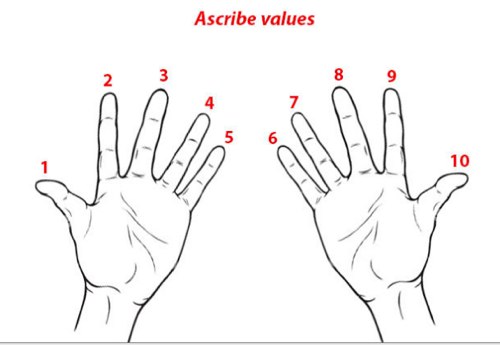
Теперь умножаем, например, 2х9. Все то, что идет до пальца №2 — это десятки (то есть 1 в этом случае). А все то, что остается после пальца №2 — единицы (то есть 8). В итоге получаем 18.
давайте посчитаем хотя бы один ряд Фурье в уме / Habr
Давайте проверим. Прочтите следующее:
Тригонометрическим рядом Фурье функции  называют функциональный ряд видагде
Значит, вам под кат. Постараюсь формул не использовать.
По моему глубокому убеждению, к математике можно подходить на двух уровнях: большинство людей её видит (им её именно так и преподают) как набор значков и правил операций над значками, что приводит к широким массам людей, математикой травмированных. А можно попытаться передать смысл и идеи, не особо заостряясь на значках. Лично я неспособен к синтаксическому подходу, я в цепи из двух формул обязательно потеряю какой-нибудь минус, что не мешает мне достаточно успешно считаться математиком. Просто у меня в голове графический ускоритель.
Actually, there was a certain amount of genuine quality to my guesses. I had a scheme, which I still use today when somebody is explaining
something that I’m trying to understand: I keep making up examples. For instance, the mathematicians would come in with a terrific theorem, and they’re all excited. As they’re telling me the conditions of the theorem, I construct something which fits all the conditions. You know, you have a set (one ball) — disjoint (two balls). Then the balls turn colors, grow hairs, or whatever, in my head as they put more conditions on. Finally they state the theorem, which is some dumb thing about the ball which isn’t true for my hairy green ball thing, so I say, «False!»
И при подготовке этого текста я наткнулся на замечательный доклад Анри Пуанкаре, который, пожалуй, был величайшим математиком конца девятнадцатого и начала двадцатого столетия. Он указывал, что даже в такой абстрактной науке, как математика, следует культивировать интуитивные понятия, например, понятие прямолинейности, хотя интуиция и должна проверяться формальными доказательствами.
Его доклад озаглавлен «Du rôle de l’intuition et de la logique en mathématiques», на французском можно прочитать тут, английский перевод доступен здесь. Крайне рекомендую интересующимся математикой, читается на одном дыхании.
Update: Вот тут лежит перевод на русский язык.
К сожалению, передавать интуицию очень сложно, но я попытаюсь, так как выгода от переданной интуиции несравнимо выше от выгоды передачи просто значков.
Перво-наперво нужно знать, что такое вектор, хотя бы на уровне «стрелочка». Ну и представлять, что стрелочки можно рисовать в существенно большем количестве размерностей, нежели 2 или 3. Ну и что хранить вектор можно в std::vector.
На пальцах скалярное произведение можно представлять как меру того, насколько один вектор похож на другой. То есть, это операция, которая на вход берёт два вектора, на выход даёт число. Нормирование данных это уже детали, пока не очень нужные. Поэтому если у меня есть две стрелочки единичной длины, то скалярное произведение равно единице, если стрелочки совпадают, нулю, если они ортогональны и минус единице, если они противонаправлены.
Это не просто лирика, это пример, который на первый взгляд не связан с темой разговора, но на самом деле является его сутью. Хотите понимать дальше — понимайте пример. Что неясно, задавайте вопросы.
Давайте на минуту рассмотрим крайне практическую задачу: у меня есть неспешный робот, и он должен знать, где он находится. Система навигации должна быть пассивной. Я люблю крайне дубовые решения, поэтому я ставлю на моего робота два микрофона (как уши у человека). Затем у меня есть маяк (на самом деле несколько, но давайте про один), который проигрывает в цикле некоторый (моно) звук. Например, вот такой:
Это просто сухие щелчки, положим для простоты один щелчок в секунду.
«Уши» робота находятся на разном расстоянии от маяка, а звук распространяется неспешно, поэтому каждый из двух микрофонов запишет плюс-минус один и тот же сигнал, но с небольшой задержкой один относительно другого. Я не ищу легких путей, поэтому у меня не лабораторные условия. Вот, например, как выглядит запись в течение нескольких секунд:
Два канала по количеству ушей, высокий уровень шума (играет музыка). На записи видно регулярные всплески сухих щелчков, но напрямую искать их в сигнале крайне непросто, иногда музыка бывает даже громче щелчков.
Как мне убрать фоновый шум? Напоминаю, робот у меня совсем неспешный. Самый дубовый способ — это записать час звука, затем порезать его на 3600 кусков в одну секунду длиной (у меня один щелчок в секунду), и взять среднее между всеми этими кусочками записи.
Получится нечто вот такое:
Пики щелчков приходятся в каждом из 3600 кусков на одно и то же место, а остальной шум размазан более-менее равномерно по всей длине, в итоге шум уходит. К слову сказать, маяков у меня несколько, никакой синхронизации между ними нет, а ушей только два. И именно так я и разделяю сигналы с маяков: один маяк щёлкает три раза в секунду, другой пять, третий семь. (Очень важно) Порезав один и тот же сигнал на кусочки в 1/3, в 1/5 или в 1/7 секунды, я получу сигнал именно с нужного маяка!
Итак, теперь мне нужно понять, как один сигнал сдвинут относительно другого. Мне абсолютно всё равно, в каком именно месте записи у меня пик, мне нужен сдвиг одного канала относительно другого.
Для начала давайте поймём, как я вообще представляю этот сигнал в памяти машины. Я пишу обычный wav с частотой дискретизации 44100Гц. Длина записи одна секунда, таким образом, у меня есть просто два массива (вектора!) вещественных чисел со 44100 элементами.
Фиксируем один вектор, а второй 44100 раз циклически сдвинем вправо. (Очень важно) Посчитаем 44100 скалярных произведения и возьмём тот сдвиг, при котором это скалярное произвдение максимально. То есть, именно этот сдвиг максимизирует похожесть двух сигналов. Поздравляю вас, вы только что посчитали взаимнокорреляционную функцию!
Update: хороший комментарий с иллюстрацией.
Предыдущая секция очень важна, но пока давайте её отложим и попробуем посчитать на пальцах простой ряд Фурье.
В качестве примера давайте возьмём простой квадратный сигнал, так любимый в электронике. Графики я рисую в sage.
def square_wave(t): return (sgn(sin(t))+1)/2
t = var('t')
plot(square_wave(t), (t, -10*pi, 10*pi),figsize=(10,2))Это простой периодический сигнал с периодом в 2 pi. Половину времени он равен нулю, половину времени равен единице. Давайте считать коэффициенты ряда Фурье (см. начало статьи).
Нулевая частота
Коэффициент a0 — это просто среднее сигнала, очевидно, что он равен половине. Как считать a1 и b1?
Первая частота
А вот тут я предлагаю нарисовать один период нашего сигнала, но на сей раз не в обычной декартовой системе координат, но в полярной. Итого у нас угол идёт от нуля до двух пи, и мы получим следующую картинку:
parametric_plot((cos(t)*square_wave(t), sin(t)*square_wave(t)), (t, 0, 2*pi))Почему в полярной системе? Очень просто. Как преобразуются полярные координаты точки (r,alpha) в декартовы?
x = r cos(alpha),
y = r sin(alpha).
А что у нас стоит под знаком интеграла в формуле для a1 и b1? Правильно, f sin(t) и f cos(t). Осталось проинтегрировать. Как это сделать в уме? Представьте, что у вас это не математический график, а отрезок проволоки. Давайте найдём его центр тяжести. Очевидно, что он будет лежать на оси ординат примерно в центре нашей дуги (на самом деле, на расстоянии 2/pi от центра, ну да это не суть, давайте назовём это расстояние A):
Координаты красной точки (центра тяжести графика) и есть нужные нам интегралы (с точностью до умножения на константу, ну да это не суть). Кстати, а можете сказать, почему именно так?
Итого a1 = 0, b1 = A.
Вторая частота
Что до a2 и b2? Давайте снова делать полярный график, «наматывая» наш обычный график вокруг нуля. Единственное, что теперь мы будем наматывать, делая два оборота.
Первый оборот:
parametric_plot((cos(2*t)*square_wave(t), sin(2*t)*square_wave(t)), (t, 0, pi))parametric_plot((cos(2*t)*square_wave(t), sin(2*t)*square_wave(t)), (t, pi, 2*pi))Второй оборот очевидно будет пустым, наш квадратный сигнал в этот момент равен нулю:
Центр масс первого + второго графиков лежит, очевидно, в нуле. Таким образом, a2=0, b2=0.
Третья частота
Теперь намотаем вокруг нуля один период нашей функции три раза, для наглядности я показываю три витка на раздельных графиках:
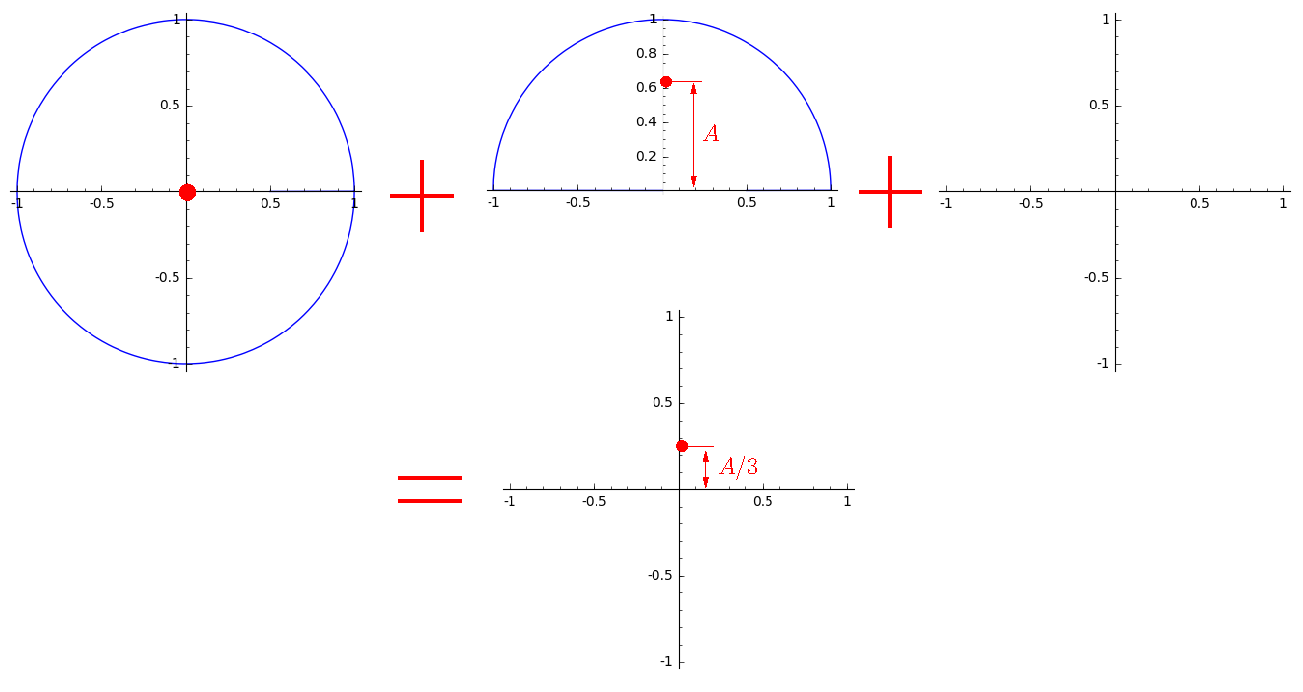
Первый виток заполняет полностью нашу окружность, второй наполовину, а третий пуст. Если один полный виток весит один килограмм, то мы имеем один килограмм в нуле и полкило на расстоянии A от нуля. Итого, центр тяжести будет на расстоянии A/3 от нуля.
a3 = 0
b3 = A/3
Более высокие частоты
Что будет с четвёртой частотой? Два заполненных витка и два пустых, центр в нуле. И так для всех чётных.
Что будет с пятой частотой? Два заполненных, два пустых и один полувиток. Итого центр тяжести на оси ординат на расстоянии A/5 от нуля.
Если посмотреть ещё раз, как мы считаем интегралы, то станет понятно, что между нашим сигналом (квадратной волной) и функциями cos(nx), sin(nx) мы ищем скалярные произведения. То есть, мы смотрим, насколько наш сигнал похож на cos(nx) и насколько он похож на sin(nx). Наматывая определённое количество раз график (периодической!) функции вокруг нуля, мы гасим все частоты, кроме текущей.
Полярный угол нашего центра тяжести говорит, насколько сигнал похож на соответствующий синус или насколько он похож на соответствующий косинус. А расстояние, на котором находится центр тяжести, говорит о силе их вклада в формирование нашего сигнала.
Итого наш ряд равен f(x) = 1/2 + 2/pi sin(x) + 2/(3 pi) sin(3x) + 2/(5 pi) sin(5x) +…
1) Вы поняли связь между примером с роботом и квадратной волной?
2) А как связан ряд Фурье с преобразованием Фурье?
Мужик считает на пальцах — Memepedia
Мужик считает на пальцах — изображение усатого мужчины в очках, который с задумчивым лицом пытается указательным пальцем правой руки пересчитать что-то на двух пальцах левой. Картинка используется для иллюстрирования ситуаций, когда «совсем плохо с математикой», и приходится буквально считать на пальцах, либо же в более юмористическом контексте — когда сказанное или увиденное плохо совпадает с реальным положением дел.
Происхождение
Фотография задумчивого мужчины в очках принадлежит фотографу Мисбаху Чоудхури. В июне 2017 года он же и выложил это фото в своем твиттере, создав первый мем на тему «что-то тут не сходится»:
Солдат, вернувшийся после 3-летнего задания наконец встретил своего двухмесячного ребенкаАвтор озадачен ситуацией с солдатом — ведь откуда у того мог взяться двухмесячный ребенок, если военного, судя по подписи на фото, не было 3 года дома. Ироничное подсчитывание пальцев высмеивает происходящее, ведь всем понятно, что эти сроки не могут совпасть, как ты их не считай.
Пользователи твиттера сначала искали самые очевидные и неочевидные варианты, которые могли привести к подобному исходу, а потом начали использовать фото «считающего» Мисбаха для собственных мемов. Юмор в таком виде и само фото с усатым мужчиной быстро набрало популярность как в твиттере, так и за его пределами.
Значение
Задумка, в целом, аналогична мему, где женщину с задумчивым лицом окружают математические формулы:
Похожий мем есть и с героем «Мальчишника в Вегасе», роль которого сыграл Зак Галифианакис:
Картинка обычно используется в двух случаях: если что то сходится, но подсчеты в этом случае будут выглядеть крайне иронично, либо же когда подсчеты, очевидно, ни к чему не приведут. Прямо как в ситуации с тем невезучим солдатом, который обязан задать своей жене пару вопросов.
Обычно мем подается либо с текстом вверху и внизу, как классический представитель жанра, либо с вставкой какого-либо изображения, которое «нормальное» только на первый взгляд. При минимальных попытках подумать, приложенная картинка мгновенно убивает всю серьезность, и вкупе с задумчивостью главного героя просто смешит общей абсурдностью.
Шаблон
Галерея
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Нескучная учеба: объяснить математику можно на пальцах
Приемы, которые помогут ученикам и их родителям.
Для родителей наступили жаркие деньки — пришла пора школьной «домашки». Хорошо, если ребенок самостоятельный и все схватывает на лету. Если нет, то было бы неплохо подятнуть дома его знания. Только не превращайте вечера в бесконечные уроки!Введите в обучение элемент игры. Мы собрали забавные приемы, которые помогут младшим школьникам лучше понять математику.
Вместо транспортира
Ладошка отчасти сможет заменить транспортир. Например, запомнить значения углов: представьте, что каждый палец обозначает угол от 0 до 90 градусов. Большой палец — 90 градусов, указательный — 60, средний — 45, безымянный — 30, мизинец — 0. Конечно, точностью такие расчеты не отличаются, но приблизительно величину углов прикинуть можно (см. рисунок).
|
|
Умножаем с помощью ладошек
Обычно дети неплохо справляются с умножением маленьких чисел. А вот все, что больше 6х7, вызывает вопросы. Сколько будет 7х8? А 6х9? Если ребенок еще не выучил толком таблицу умножения, помогут собственные ладошки.
Представим, что две ладони — это два числа, которые надо умножить друг на друга. Запоминаем правила: один загнутый палец — это число 6, два загнутых пальца — число 7, три загнутых пальца — это 8, а четыре загнутых пальца — это 9. То есть если надо умножить семь на восемь, то на одной ладони загибаем два пальца (см. рисунок), а на другой — три.
Теперь считаем, сколько всего пальцев согнуто, это будут десятки в ответе. В нашем примере загнуто 5 пальцев, это будет 50. Затем умножаем число незагнутых пальцев на одной ладони и на другой — это будут единицы. В нашем примере надо умножить 2 на 3, это будет шесть. Совмещаем десятки и единицы — получается 56.
Увы, со всем, что меньше 6х8, это правило не работает.
|
|
Правило бабочки
Говоря научным языком, это визуализация алгоритма, которая поможет научиться складывать и вычитать простые дроби. Рисуем «крылья» бабочки — объединяем числители и знаменатели дробей. Умножаем их крест-накрест и пишем получившиеся значения в «усиках» бабочки. Теперь складываем или вычитаем их — в зависимости от того, что нужно сделать в задании. Получившийся результат — это и есть итоговый числитель.
Теперь нужно разобраться с нижней частью дроби. Для этого рисуем «хвостик» бабочки — умножаем нижние части дробей друг на друга. Это и будет знаменатель (см. рисунок).
|
|
Умножение на 9
Умножать на 9 при помощи пальцев проще всего. Для этого надо мысленно (ну или фломастером) пронумеровать пальцы на обеих руках от 1 до 10. Затем загибаем палец под тем числом, на которое надо умножить 9. То есть если в примере 9х3, загибаем третий (средний) палец левой руки. Затем смотрим, сколько пальцев осталось прямыми до загнутого (это будут десятки) и после него (это будут единицы). В нашем примере будет 2 пальца до загнутого безымянного и 7 после — то есть 27 (см. рисунок).
|
|
КСТАТИ
Не только цифры
Памятка для других уроков
Нет чулок или чулков? Носков или носок? Помним: что короче, то длиннее пишется, и наоборот! Правильно: нет чулок, нет носков.
Для тех, кто путает «надеть» и «одеть»: надеть одежду, одеть Надежду.
Ударение в слове «торты»
Долго ели тОрты,
Не налезли шорты.
Три закона Ньютона
1. Не пнешь — не полетит: всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
2. Как пнешь, так и полетит: изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
3. Как пнешь, так и получишь: действию всегда есть равное и противоположное противодействие; взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.
Стишки для геометрии
Биссектриса — это такая крыса,
Которая бегает по углам
И делит угол пополам.
***
Медиана — это обезьяна,
Которая ползает по сторонам
И разделяет стороны пополам.
Учим римские цифры
Mы — 1000
Dаем — 500
Cоветы — 100
Lишь — 50
Xорошо — 10
Запоминаем планеты
«Мы Все Знаем: Мама Юли Села Утром На Пилюли» — Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон.
Справедливости ради скажем, что 2006 году ученые исключили Плутон из числа планет Солнечной системы и перевели в разряд карликовых планет.