Интуитивная математика – Ментальная арифметика – что это такое? Как научиться ментальной арифметике в домашних условиях?

Интуиционизм — Википедия

Материал из Википедии — свободной энциклопедии

Интуициони́зм — совокупность философских и математических взглядов, рассматривающих математические суждения с позиций «интуитивной убедительности». Различаются две трактовки интуиционизма: интуитивная убедительность, которая не связана с вопросом существования объектов, и наглядная умственная убедительность.

В интуиционистской математике отвергается подход классической теории множеств (в частности, не принимаются аксиома выбора и аксиома регулярности) и ряд рассуждений классической логики. Абстракция потенциальной осуществимости, которая используется в интуиционистской математике, лучше соотносится с действительностью, чем абстракция актуальной бесконечности.

В интуиционистской математике суждение считается истинным, только если его можно доказать некоторым «мысленным экспериментом». То есть истинность утверждения «Существует объект x, для которого верно суждение A(x)» доказывается построением такого объекта, а истинность утверждения «

A или B» доказывается либо доказательством истинности утверждения A, либо доказательством истинности утверждения B. Отсюда, в частности, следует, что утверждение «A или не A» может быть не истинным, а закон исключённого третьего неприемлем. Истинным математическим суждением является ряд выполненных построений эффективного характера с использованием интуиционистской логики. Эффективность не обязательно связана с наличием алгоритма и может зависеть от физических и исторических факторов, фактического решения проблем^[1].

Основными объектами исследования интуиционистской математики являются конструктивные объекты: натуральные и рациональные числа, конечные множества конструктивных объектов со списком элементов, свободно становящиеся последовательности (последовательности выбора, каждый член которых может быть эффективно доступен), интуиционистские виды (свойства, которыми могут обладать объекты исследования). Свободно становящиеся последовательности различают в зависимости от степени информации, известной исследователю. Если закон формирования последовательности известен полностью, то её называют заданной законом, если известен только начальный отрезок — беззаконной. Виды строятся в иерархию, когда элементы вида определяются независимо от самого вида, что позволяет избегать антиномий. Виды редко являются объектами исследования, большинство результатов интуиционистской математики можно получить без их использования

[1].

Интуиционизм и другие математические подходы[править | править код]

В трактовке теории множеств не делается различие между абстрактными объектами и объектами, существование которых можно подтвердить построением. В классической математике на бесконечные множества экстраполировали свойства и законы конечных совокупностей. При этом не существует способа эффективного построения объектов, что находит своё отражение в так называемых «теоремах чистого существования». Отсутствие возможности построения не имеет связи с антиномиями теории множеств и относится ко всем разделам математики

[1].

Значительное влияние друг на друга оказали концепции формализма и интуиционизма. Содержательные критерии метаматематики, необходимые для обоснования непротиворечивости формальных теорий, обычно уточняются в рамках интуиционизма. В то же время, ряд результатов интуиционистской логики был получен с помощью формализации метода^[1].

В широкой трактовке конструктивное направление математики можно рассматривать как часть интуиционистской математики^[1].

Критика теории множеств привела к возникновению двух течений: интуиционизма Лёйтзена Эгберта Яна Брауэра и формализма Давида Гильберта. В 1904 году Брауэр подверг развёрнутой критике ряд концепций классической математики. Его внимание привлёк статус существования: можно ли потенциально построить такие объекты исследования, как неизмеримое множество действительных чисел, нигде не дифференцируемая функция? Можно ли полагать, что в окружающем мире существуют бесконечные множества объектов

[1]?

Интуиционистская математика в трактовке Брауэра — это убедительность мысленных построений, не связанная вопросом существования объектов. Другая трактовка — это «наглядная умственная убедительность простейших конструктивных процессов реальной действительности». Брауэр возражал против формализации интуиционизма^[1].

Аренд Гейтинг сформулировал интуиционистское исчисление предикатов и интуиционистское арифметическое исчисление, Альфредом Тарским была открыта топологическая интерпретация, а Андреем Николаевичем Колмогоровым — интерпретация в виде исчисления задач. Понимание в форме рекурсивной реализуемости было предложено Стивеном Коулом Клини и поддержано научной школой Андрея Андреевича Маркова. К 70-м годам XX века было завершено построение теории свободно становящихся последовательностей^[1].

1. ↑ ^{1 2 3 4 5 6 7 8} Виноградов И. М. Интуиционизм // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 2.

Интуиционистское исчисление высказываний — Википедия

Материал из Википедии — свободной энциклопедии

Интуициони́стское исчисле́ние выска́зываний, называемое иногда Интуициони́стской ло́гикой — формальная система, отражающая некоторые способы рассуждений, приемлемые с точки зрения интуиционизма. Предложена А. Гейтингом в 1930.

Основное отличие от привычного исчисления высказываний заключается в том, что отсутствует закон исключённого третьего.

Схемы аксиом 1-10 и правило «модус поненс» задают интуиционистское исчисление высказываний. Все 12 схем аксиом и все 3 правила вывода задают интуиционистское исчисление предикатов. Интуиционистское исчисление предикатов отличается от классического тем, что в последнем вместо схемы аксиом 10 используется схема аксиом ((¬¬A)→A{\displaystyle ((\neg \neg A)\to A}.

[1].

∧{\displaystyle \land } (знак конъюнкции), ∨{\displaystyle \lor } (знак дизъюнкции), →{\displaystyle \to } (знак импликации) и ¬{\displaystyle \neg } (знак отрицания).

Далее через A{\displaystyle A}, B{\displaystyle B} и C{\displaystyle C} обозначаются произвольные пропозициональные формулы.

1. (A→(B→A)){\displaystyle (A\to (B\to A))}
2. ((A→B)→((B→C)→(A→C))){\displaystyle ((A\to B)\to ((B\to C)\to (A\to C)))}
3. (A→(B→(A∧B))){\displaystyle (A\to (B\to (A\land B)))}
4. ((A∧B)→A){\displaystyle ((A\land B)\to A)}
5. ((A∧B)→B){\displaystyle ((A\land B)\to B)}
6. (A→(A∨B)){\displaystyle (A\to (A\lor B))}
7. (B→(A∨B)){\displaystyle (B\to (A\lor B))}
8. ((A→C)→((B→C)→((A∨B)→C))){\displaystyle ((A\to C)\to ((B\to C)\to ((A\lor B)\to C)))}
9. ((A→B)→((A→(¬B))→(¬A))){\displaystyle ((A\to B)\to ((A\to (\neg B))\to (\neg A)))}
10. ((¬A)→(A→B)){\displaystyle ((\neg A)\to (A\to B))}
11. ∀xA(x)→A(y){\displaystyle \forall xA(x)\to A(y)}
12. A(y)→∃xA(x){\displaystyle A(y)\to \exists xA(x)}

1. Modus ponens: A,(A→B)B{\displaystyle {\frac {A,\;(A\to B)}{B}}}.
2. C→A(x)C→∀xA(x){\displaystyle {\frac {C\to A(x)}{C\to \forall xA(x)}}}
3. A(x)→C∃xA(x)→C{\displaystyle {\frac {A(x)\to C}{\exists xA(x)\to C}}}

1. ↑ В. Е. Плиско Интуиционистская логика. — Математический энциклопедический словарь. — М., Советская энциклопедия, 1988. — Тираж 150 000 экз. — c. 243

• Гейтинг А. Интуиционизм. — М., 1965.
• Клини С. К. Введение в метаматематику. — М., 1957.
• Новиков П. С. Конструктивная математическая логика с точки зрения классической. — М., 1977.
• Драгалин А. Г. Математический интуиционизм. Введение в теорию доказательств. — М., 1979.

интуитивная математика — это… Что такое интуитивная математика?



интуитивная математика

мат. intuitive mathematics

Большой англо-русский и русско-английский словарь. 2001.

• интуитивная вероятность
• интуитивная переменная

Смотреть что такое «интуитивная математика» в других словарях:

• ИНТУИЦИОНИЗМ — (от позднелат. intuitio, от лат. intueor пристально смотрю) направление в обосновании математики и логики, согласно которому конечным критерием приемлемости методов и результатов этих наук является наглядно содержательная интуиция. Вся математика …   Философская энциклопедия

• Интуиционизм — Интуиционизм  система философских и математических идей и методов, связанных с пониманием математики как совокупности «интуитивно убедительных» умственных построений. С точки зрения интуиционизма, основным критерием истинности… …   Википедия

• Интуиционистская логика — Интуиционизм  система философских и математических идей и методов, связанных с пониманием математики как совокупности «интуитивно убедительных» умственных построений. С точки зрения интуиционизма, основным критерием истинности математического… …   Википедия

• множеств теория —         МНОЖЕСТВ ТЕОРИЯ учение о множествах, зародившееся в середине 19 в. и изучающее свойства множеств произвольной природы. Создание М. т. было подготовлено работами математиков, ставивших целью разработку оснований анализа. Первые работы в… …   Энциклопедия эпистемологии и философии науки

• ЛОГИКА В РОССИИ — эволюция современной (математической) логики в России. Кон. 19 в. и нач. 20 в. знаменуют выход логики за рамки силлогистики и появление логиков новаторов, таких как П.С. Порецкий, М.В. Каринский, Л.В. Рутковский, СИ. Поварнин, и др. Казанский… …   Философская энциклопедия

• ТЕОРИЯ ПОЗНАНИЯ — Гносеология (от греч. gno sis знание, logos слово, понятие), Эпистемолог и я (от греч. episteme знание) раздел философии, исследующий природу человеческого познания, его источники и предпосылки, отношение знания к предмету познания, условия… …   Философская энциклопедия

• ИНТУИЦИОНИЗМ — совокупность философских и математич. идей и методов, рассматривающих математику как науку об умственных построениях. С точки зрения И., основным критерием истинности математич. суждения является интуитивная убедительность возможности построения… …   Математическая энциклопедия

• Кант Иммануил — Жизненный путь и сочинения Канта     Иммануил Кант родился в Кенигсберге (ныне Калининград) в Восточной Пруссии в 1724 г. Отец был шорником, а мать домохозяйкой, шестеро их детей не дожили до зрелого возраста. Кант всегда вспоминал родителей с… …   Западная философия от истоков до наших дней

• ИНТУИЦИОНИСТСКАЯ ЛОГИКА — одна из наиболее важных ветвей неклассической логики, имеющая своей филос. предпосылкой программу интуиционизма. Выдвигая на первый план математическую интуицию, интуиционисты не придавали большого значения систематизации логических правил.… …   Философская энциклопедия

• Парадигма — (Paradigm) Определение парадигмы, история возникновения парадигмы Информация об определении парадигмы, история возникновения парадигмы Содержание Содержание История возникновения Частные случаи (лингвистика) Управленческая парадигма Парадигма… …   Энциклопедия инвестора

• ЧИСЛО — Понятие числа в математике может относиться к объектам различной природы: натуральным числам, используемым при счете (положительным целым числам 1, 2, 3 и т.д.), числам, являющимся возможными результатами (идеализированных) измерений (это такие… …   Энциклопедия Кольера

Математическая интуиция (стр. 1 из 5)

Введение.

Еще древних интересовали вопросы: как создается новое, откуда берется то, чего еще не было вчера, кто или что является его источником? И уже древние пытались на него ответить, создавая грандиозные мифологические, потом религиозно-философские, а затем и научные картины мира. Однако в отношении творений человека этот вопрос приобретал особую остроту. Ибо, во-первых, пути поиска нового, даже в одной области, зачастую очень сильно разнятся, а во-вторых, способность создавать новое присуща далеко не всем людям.

Деятельность человека, порождающая качественно новое, оригинальное и уникальное, получила название творчество. По-видимому, первые попытки рациональной реконструкции творческого процесса начались в античности, причем тогдашние мыслители имели в своем распоряжении достаточно развитую математику. Поэтому практически все их исследования так или иначе касались ее. Уже античные авторы заметили специфичность математики, которая заключалась в воплощении принципов логической последовательности выводов из принятых постулатов. В таком подходе они увидели идеал, к которому нужно было привести остальные области знания — философию, физику, астрономию и др. Но в последствии от этого отказались и на смену математическому идеалу пришли другие.

Дальнейшие исследования только подчеркнули обособленность математики, уникальность ее методов и выводов, что позволяет говорить нам об особом виде творчества — математическом творчестве. Нас будет интересовать вопрос, как осуществляется это творчество, т.е. появляется новое в математике, и какова роль интуиции в появлении этого нового. Кроме того, мы рассмотрим некоторые вопросы взаимоотношений математической интуиции и гуманитарного знания.

Интуиция в математическом творчестве.

“Чистая логика всегда приводила бы нас только к тавтологии; она не могла бы создать ничего нового…”

А. Пуанкаре [17, стр.210]

Виды интуиции.

Во введении мы отметили, что процесс открытия одного и того же может протекать у разных людей по-разному. Это не удивительно, т.к. в каждом таком случае мы имеем дело с творческой индивидуальностью, которая во многом определяется работой уникального органа – человеческого мозга. Раскрытие механизмов его работы могло бы дать точный ответ на наши вопросы. Но до сих пор эти механизмы остаются загадкой. Более того, современные исследования подчеркивают сложность их раскрытия. Так, И. Пригожин и И. Стенгерс приводили следующие интересные сведения: “В стадии глубокого сна в <электрической> активности головного мозга обнаруживается детерминистический хаос с фрактальным аттрактором в шестимерном пространстве<…> С другой стороны, в состоянии бодрствования конечномерный аттрактор не был идентифицирован. С точки зрения электрической активности мы имеем дело с истинной случайностью” [16, стр. 78]. Это говорит о том, что исследование процесса творчества через изучение функционирования головного мозга не может сегодня существенно помочь в достижении наших целей. Казалось бы, на этом можно ставить точку в попытке изучения творчества вообще и математического – в частности, объявив эту задачу пока неразрешимой. Такая негативная реакция вполне естественна. Однако, там где мы доходим до границ специального знания, где мы осознаем принципиальную ограниченность этого знания и где у нас возникает потребность перешагнуть эти границы, там у нас остается одно средство – это гипотеза и философский анализ проблемы. Здесь мы встаем на этот путь. Его суть заключается в изучении свидетельств субъектов творчества и его продуктов. Как мы увидим, такой путь позволит хотя бы частично ответить на заявленные вопросы.

Исследователи давно заметили два совершенно различных магистральных пути в понимании математики: геометрический (или топологический) и алгебраический. Геометрический способ понимания включает в себя оперирование наглядными идеями, привлечение чертежей и рисунков, отказ, хотя бы на этапе самого творения, от формул и вычислений, огрубляя, можно сказать так: геометрическое понимание – это сначала наглядное представление, потом формула. Под алгебраическим способом понимают полную противоположность геометрическому. Несмотря на то, что оба подхода можно достаточно четко идентифицировать, они не являются самодостаточными. Т. е. не всегда задача может быть сведена только к геометрии или только к алгебре. Заметим, что в истории были попытки такого сведения.

В VI в. до н. э. пифагорейцы выдвинули философский принцип – “все есть число”. И попытались все известные им закономерности свести к числовым соотношениям. Однако открытие проблемы несоизмеримости отрезков привело к отказу от этого принципа и переходу к геометрическому способу рассуждений. Такой подход просуществовал довольно долго. Например, Д. Кардано (1501-1576) при выводе своих знаменитых формул рассуждал примерно так: “… если куб со стороной β=α+х разрезать плоскостями, параллельными граням, на куб со стороной α и куб со стороной х, получается, кроме двух кубов, три прямоугольных параллелепипеда со сторонами α, α, х и три – со сторонами α, х, х; соотношение между объемами дает

х³+3х²α+ 3хα² +α³ = β³ ;

для перехода к

х³+3αβх = β³-α³

параллелепипеды разных типов попарно объединяются.” [9, стр. 27]

Т. о. выглядела привычная нам выкладка 3х²α +3хα²=3хα (х+α)= 3хαβ (с учетом того, что х+α=β).

Переход на алгебраическую символику, в частности открытие аналитической геометрии, существенно упростили рассуждения. И позволил студентам-первокурсникам просто решать задачи, многие из которых потребовали бы значительных усилий у великих математиков древности.

Как видим, применение геометрического подхода в данной задаче затрудняло ее решение, а алгебраическая символизация существенно упростила ее понимание.

Более того, в любой содержательной задаче можно выделить как геометрическую, так и алгебраическую составляющие, причем составляющие независимые. Простой пример – это понятие действительного числа. Вот, что пишет по этому поводу Г. Вейль [8]: “Система действительных чисел подобна двуликому Янусу: с одной стороны – это совокупность алгебраических операций “+” и “” и им обратных, с другой – континуальное многообразие, части которого связаны друг с другом непрерывно. Первый лик чисел алгебраический, второй топологический.”

Необходимо отметить, что сочетание обоих подходов жизненно необходимо для развития математики. Мы частично продемонстрировали это на примере вывода формул Кардано. Приведем еще несколько свидетельств в пользу нашего вывода. Так, известно, что основную теорему алгебры невозможно доказать чисто алгебраическими методами. На каком-то этапе нам обязательно потребуется свойство непрерывности в той или иной геометрической интерпретации.

Или возьмем понятие группы Ли. Как отмечает выдающийся специалист в области группового анализа дифференциальных уравнений П. Олвер [12]:

“На первый взгляд группа Ли выглядит каким-то неестественным сочетанием алгебраического понятия группы, с одной стороны, и дифференциально- геометрического понятия многообразия <…>, однако <…> комбинация алгебры и анализа приводит к мощной технике для изучения симметрии … ” [12, стр. 37-38].

Итак, мы выделили два направления в понимании математики. Причем указали на их принципиальную взаимодополняемость или на то, что Г. Вейль называл “предустановленной гармонией между геометрией и алгеброй”. Изучение творчества реально действующих математиков показывает, что последние всегда тяготеют к какому-то одному из направлений. Классическим примером является школа теории функций К. Вейерштрасса с формально-алгебраической направленностью и топологическая теория алгебраических функций Г. Римана. Такое разделение скорее всего является не только действием окружающих факторов. Так, те же К. Вейерштрасс и Г. Риман творили в одно и то же время, в одной и той же культурной среде. Поэтому с большой долей вероятности можно утверждать, что в основе такого пристрастия лежат личные мотивы, основой которых является, при прочих равных условиях, физиологические особенности головного мозга конкретного ученого. В подтверждение сошлюсь на открытие, сделанное профессором Калифорнийского технического института Р. Сперри. Р. Сперри исследовал больных с перерезанным “мозолистым телом”, соединяющим два полушария мозга и доказал, что функции этих полушарий обладают определенной несимметричностью. За свои исследования Р. Сперри получил Нобелевскую премию по биологии и медицине в 1981 году. Коротко суть открытия Р. Сперри сформулировал академик В. И. Арнольд: “Наш мозг состоит из двух полушарий. Левое отвечает за умножение многочленов, языки, шахматы, интриги и последовательности силлогизмов, а правое – за пространственную ориентацию, интуицию и все необходимое для реальной жизни” [2, стр. 49].

Т. о., можно принять разделение математиков на “правополушарных” и “левополушарных”. “Левополушарных” будем еще называть аналитиками или алгебраистами. Рассмотрим более подробно “правополушарных” математиков. Эту категорию называют еще геометрами. Но в силу того, что “правополушарные” математики черпают свои идеи не только из пространственных представлений, такое название кажется слишком узким. Кроме, собственно, геометрических представлений к математическому открытию могут вести представления из смежных областей знания. Наиболее ярко это проявляется во взаимоотношениях математики и физики. Причем физика не только ставит задачи, она так же является поставщиком новых понятий и методов. Так, основные факты теории обобщенных функций появились исходя из чисто физических абстракций и были сформулированы и использованы задолго до строгих математических обоснований. А упоминавшийся выше В. И. Арнольд вообще указывает на “фундаментальное единство математики и физики” [6, стр. 10].

Интуиционистская логика — это… Что такое Интуиционистская логика?

Интуициони́зм — система философских и математических идей и методов, связанных с пониманием математики как совокупности «интуитивно убедительных» умственных построений. С точки зрения интуиционизма, основным критерием истинности математического суждения является интуитивная убедительность возможности проведения мысленного эксперимента, связываемого с этим суждением. Поэтому в интуиционистской математике отвергается теоретико-множественный подход к определению математических понятий, а также некоторые способы рассуждения, принятые в классической логике.

Интуиционистская математика является достаточно разработанным направлением, которое достигло многих существенных результатов, в том числе и в таких областях, как теория меры, функциональный анализ, топология, теория дифференциальных уравнений.

Критика классической математики

Отдельные черты интуиционизма можно проследить ещё в античной математике, а позднее в высказываниях таких учёных, как Гаусс, Кронекер, Пуанкаре, Лебег, Э.Борель. Однако в своём современном виде интуиционизм возник как результат критического пересмотра основ классической математики, проведённого начиная с 1907 года Л. Э. Я. Брауэром.

В основе критики Л. Э. Я. Брауэра лежит вопрос о природе математических объектов и суждений о них. Так, естественно представить, что произвольное натуральное число может быть построено в виде последовательного ряда однородных предметов, например, ряда точек. Столь же естественно представить, что, построив некоторое натуральное число, можно построить затем и следующее, добавив к уже построенному ещё одну точку. Поэтому природа натуральных чисел является интуитивно ясной. Однако наряду с такими объектами в классической математике рассматриваются и объекты с интуитивно неясной природой, например, «множество всех натуральных чисел» и «множество, неизмеримое по Лебегу». С ними не связывается никакого способа их мысленного построения, и потому их действительное существование представляется сомнительным.

Одним из источников возникновения такого рода «монстров» в классической математике являются теоремы чистого существования, в которых наличие искомого объекта утверждается лишь на основе формального опровержения гипотезы о его невозможности. Иначе говоря, фундамент таких теорем составляет представление об абсолютной непогрешимости законов классической логики.

Это представление также стало одной из мишеней критики Брауэра. С его точки зрения, законы классической логики возникли в результате рассмотрения конечных совокупностей, при работе с которыми доказательство чистого существования заведомо может быть дополнено эффективным способом построения искомого объекта — полным перебором. При переходе же к рассмотрению бесконечных совокупностей эти законы становятся недостоверными, поскольку полного перебора таких совокупностей мы провести уже не можем.

В качестве простейшего примера рассмотрим следующую теорему чистого существования:

«для любого вещественного числа x найдётся натуральное число n, равное 1 в случае x = 0, и равное 2 в случае »

Признать такое число n действительно существующим мы могли бы лишь в том случае, если бы умели сравнивать произвольное вещественное число x с нулём, чего, однако, мы делать не умеем. Действительно, число x на деле задаётся некоторой бесконечной последовательностью рациональных чисел 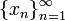. Эффективным способом сравнения числа x с нулём был бы лишь такой, который позволял бы производить это сравнение на основе просмотра некоторого конечного (пусть и очень большого) набора чисел x_k. Однако такое рассмотрение не позволяет надёжно установить верность равенства x = 0.

Аналогичные трудности возникают при попытках прояснения статуса существования многих других объектов классического анализа, например, точек экстремума непрерывной функции на отрезке, нулей знакопеременных непрерывных функций на отрезке и т. д. Никакого способа эффективного построения указанных объектов в нашем распоряжении не имеется.

Такая критика классической математики не связана непосредственно с антиномиями теории множеств. Появление антиномий можно рассматривать как дополнительный довод в пользу неудовлетворительности теоретико-множественного подхода, но критика относится и к таким разделам математики, где антиномий не возникает.

Интуиционистская логика

Для более ясной формулировки интуиционизма последователь Л. Э. Я. Брауэра А. Гейтинг создал интуиционистскую логику.

При построении интуиционистской математики обычные логические связки, употребляемые для формулировки математических суждений, истолковываются способом, отличным от классического. Любое суждение считается осмысленным, только если оно выражает возможность некоторого умственного построения, и считается истинным, только если исследователю удалось выполнить соответствующее построение. Так, утверждение, начинающееся с квантора существования, означает наличие способа мысленного построения искомого объекта. Дизъюнкция 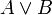суждений A и B означает возможность непосредственно указать среди этих суждений верное. С этой точки зрения, суждение вида 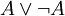может и не быть истинным, если проблема A не решена к настоящему времени. Отсюда видно, что закон исключённого третьего неприемлем в интуиционистской математике в качестве логического принципа.

Соотношение теоретико-множественной, интуиционистской и конструктивной математик с точки зрения допускаемых логических средств и абстракций может быть охарактеризовано следующей таблицей:

1. ↑  Отказ от абстракции актуальной бесконечности провозглашался как один из принципов интуиционизма, в то же время, впоследствии было показано, что использование принятого в интуиционизме аппарата построений на деле означает привлечение абстракции актуальной бесконечности.

2. ↑  Эффективность в интуиционизме понимается достаточно широко, она не обязательно связана с наличием алгоритма в точном понимании этого термина и может носить, например, характер исторического наступления события, зависеть от фактического решения проблем, от физических факторов.

Объекты исследования

Объектами исследования интуиционистской математики являются прежде всего конструктивные объекты, такие, как натуральные числа, рациональные числа, списки конструктивных объектов. Кроме того, характерной чертой интуиционизма, отличающей его от конструктивной математики, является рассмотрение свободно становящихся последовательностей математических объектов (то есть неограниченно продолжающихся и не управляемых никаким заранее определённым законом процессов выбора таких объектов). Рассмотрение свободно становящихся последовательностей связано с привлечением абстракции актуальной бесконечности (отказ от которой в интуиционизме, таким образом, не является абсолютным).

Требование интуитивной ясности используемых понятий и проводимых конструкций приводит к тому, что некоторые разделы традиционной математики приобретают в интуиционизме весьма необычный вид. Числовой континуум трактуется не как совокупность отдельных точек, а как «среда становления», поток измельчающихся рациональных интервалов. Каждое отдельное интуиционистское вещественное число определяется как свободно становящаяся последовательность неограниченно уменьшающихся вложенных друг в друга рациональных интервалов. В рассуждениях об интуиционистском числовом континууме (и вообще, в интуиционистской теории потоков) применяется ряд тесно связанных с представлением о свободном становлении логических принципов, основным из которых является бар-индукция. Это позволяет, в частности, утверждать, что всякая интуиционистская вещественная функция, определённая на отрезке, равномерно непрерывна.

Рецепция принципов и методов интуиционизма в других направлениях математики

Сторонники интуиционизма не связывают свои воззрения с какими бы то ни было логическими системами. Так, один из виднейших интуиционистов А. Гейтинг утверждал, что «логика — не та почва, на которой мы стоим», и что формализовать можно лишь завершённую часть интуиционистской математики (развивающиеся же её части могут потребовать существенного пересмотра используемых логических средств). В конце жизни он даже высказывал сожаление, что его известность связана в значительной степени с предложенной им системой логических правил, допустимых с точки зрения интуиционизма уже ввиду их формы. Дело в том, что в исследовании этой системы (получившей известность под неточным названием «интуиционистского исчисления высказываний») приняли значительное участие и математики, не разделявщие взглядов интуиционизма, и пытавшиеся сводить всё его содержание к набору логических правил Гейтинга. В настоящее время мнение о возможности такого сведения является одним из основных математических предрассудков, касающихся интуиционизма.

Как и подавляющее большинство математиков, интуиционист А. Гейтинг вместе с другими последователями школы Л. Э. Я. Брауэра признает объективность математических истин, их включенность в структуру действительности, но, говорит он, описание того, каким именно образом математические истины включены в реальность, математики дать не в состоянии. Таким образом, можно вполне определенно утверждать наличие реалистических установок в интуиционистском понимании природы математического знания в целом.

Тем не менее, исследования интуиционистского исчисления высказываний и основанных на нём формальных теорий представляют и самостоятельный интерес. В частности, была открыта топологическая интерпретация этого исчисления (А. Тарский) и его интерпретация в виде исчисления задач (А. Н. Колмогоров). Была доказана независимость логических связок и невозможность представления интуиционистской логики высказываний в виде конечнозначной логики (К. Гёдель). А. Гейтинг описал интуиционистское арифметическое исчисление, которое получается, если классическое арифметическое исчисление рассматривать на базе интуиционистского исчисления предикатов.

Для исчисления предикатов и арифметического исчисления Колмогоров и Гёдель предложили погружающую операцию классического исчисления в негативный фрагмент соответствующего интуиционистского исчисления (позволяющую, в частности, сводить вопрос о непротиворечивости классического исчисления к аналогичному вопросу для соответствующего ему интуиционистского). Были установлены свойства интуиционистской дизъюнкции и существования, состоящие в том, что если выводимо предложение 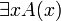, то для некоторого терма t выводимо A(t), и если выводимо предложение 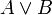, то выводимо одно из предложений A и B.

В 1945 году С. К. Клини предложил новый вариант интуиционистского понимания арифметических суждений, основанный на развитой в 1930-е годы теории алгоритмов и получивший известность под именем рекурсивной реализуемости. Дальнейшая разработка этого понимания и связанных с ним идей в научной школе А. А. Маркова привела к возникновению современной конструктивной математики.

Литература

• Гейтинг А. Интуиционизм. — М.: Мир, 1965.

• Вейль Г. О философии математики. — М.-Л.: ГТТИ, 1934.

• Клини С., Весли Р. Е. Основания интуиционистской математики с точки зрения теории рекурсивных функций / Пер. с англ. — М., Наука, 1978. — 272 с.

Wikimedia Foundation. 2010.

Развитие математической интуиции учащихся

Евдокимова Ирина Сергеевна, студент,ФГБОУ ВО «Смоленский государственный университет», г. Смоленска[email protected]

Шатохина Анастасия Андреевна,студент,ФГБОУ ВО «Смоленский государственный университет», г. Смоленска[email protected]

Развитие математической интуиции учащихся

Аннотация. В статье рассматриваются роль и место интуиции в математике, соотношение интеллектуального мышления и интуитивного созерцания. Авторами подчеркивается специфика математической интуиции в изучении самого предмета. Выявляется особенность интуиции при формировании математических теорий. В статье приведены примеры применения интуитивного мышления на разных этапах деятельности при изучении математики.Ключевые слова: математическая интуиция, предзнание, послезнание, оценка ситуации, прикидка, анализ.

В условиях перехода системы образования на новые федеральные государственные образовательные стандарты требования к качеству математического образования учащихся серьезно возросли, что приводит к необходимости в дальнейшем совершенствования теории и методики обучения математике. Важный резерв совершенствования методики обучения, усиления ее развивающей составляющей заключается в объединениианалитической левополушарной деятельности, доминирующей сегодня в реальном учебном процессе, с правополушарной, придающей этой деятельности синтетическую творческую направленность. В связи с этим необходимо в большей степени придавать значение исследованию проблемы интуиции в учебном математическом познании учащихся.Ряд известных учёных(Ж. Адамар, К. Дункер, Ю.М. Колягин, Н. Майер, А.И. Маркушевич, Д.Д. МордухайБолтовский, А. Пуанкаре, В. Хаекер, А.Я. Хинчин, Т. Циген,

С.И. Шварцбурд и др.)—математиков, психологов, педагогов, методистов —указывают на значительную роль интуиции в процессе обучения математике и на важность развития интуиции учащихся. «Главная цель обучения математике —это развить известные способности ума, а между этими способностями интуиция отнюдь не является наименее ценной», —писал французский математик А. Пуанкаре[1, с. 359].Его мнение разделял русский математик В. А. Стеклов: «Метод открытия и изобретения один и тот же, та же интуиция, ибо при помощи логики никто ничего не открывает» [2, с. 68].Математическая интуиция имеет сложную структуру и представляет собой неалгоритмический процесс. Постановка задачи, размышление, упорные поиски, накопление знаний и умений, творческие усилия и воля, страстность и одержимость, высокое осознание необходимости достижения определённого результата в своей познавательной деятельности —все этопорождает интуицию как эвристический феномен.Очень интересно определяет роль математической интуиции в обучении математике Ян Стюарт: «Я не могу объяснить, что я сам понимаю под интуицией. Просто это то, чем живет настоящий математик (или физик, инженер, поэт). Интуиция позволяет ему «ощущать» свой предмет, видеть, что теорема верна, еще не зная ее формального доказательства, а потом придумывать это доказательство[3, c136].Практически каждый человек в какойто мере обладает математической интуицией. Ею наделен ребенок, складывающий картинку из кубиков, ею обладает всякий, кому удалось уложить вещи в багажник автомобиля, перед тем как всей семьей отправиться на нем в отпуск.Главной целью подготовки математиков следовало сделать оттачивание их интуиции до такой степени, чтобы она превратилась в управляемое орудие исследования.Возможности развития интуиции включены и не столько в содержании обучения, сколько в его методах, в специально ориентированный на этой работе учителя. И такая работа должна быть поддержана способствующие методической литературой, которой пока еще недостаточно. Здесь мы хотим привести несколько общих положений, относящихся к развитию математической интуиции, и подкрепить их примерами.Возможности развития интуиции заключены не столько в содержании обучения, сколько в его методах, в специально ориентированной на этой работе учителя. И такая работа должна быть поддержана соответствующей методической литературой, которой пока еще недостаточно. Здесь мы хотим привести несколько общих положений, относящихся к развитию математической интуиции, и подкрепить их примерами.Одно из проявлений математической интуиции учащихся состоит как бы непосредственном ведении тех или иных математических понятий и фактов без строгих формальных определений и дедуктивных выводов. Такое видение может либо предшествовать систематическому изучению соответствующего раздела математики (предзнание), либо появляется в результате этого изучения (послезнание).Предзнание лежит по сути в основе всего обучения математике в школе, так как, за крайний редкими исключениями, учащийся может понять формально строгое определение только после его усвоения на интуитивном уровне. При этом необходимо специальная работа по развитию интуитивного предзнания не только непосредственно перед введением понятия, но и задолго до этого, особенно для более важных понятий и фактов. С этой целью следует по возможности раньше употреблять соответствующие термины (линия, фигура, тело, длина, площадь, объем, касательная, выпуклость, приближённое равенство и т.п.), даваяим наглядное пояснение;приводить соответствующие факты (площадь целого больше площади частей и равна сумме площадейчастей,составляющих данную фигуру,и т.п.) и предлагать упражнения,направленные наихзакрепление в сознании учащихся.Интуитивное послезнание.Интуитивное знание развивается в основном при разборе конкретных ситуаций–примеров,задач,картинок. Для этого нужно сопровождать такой разбор краткими, пусть огрубленнымиформулировками основных понятий,фактов,идей,на которые желательно направить внимание учащихся.Например:«В этой задаче два неизвестных, поэтому мы составили два уравнения,так как число уравнений должно равняться числу неизвестных»;«Обратите внимание, что она рассматриваемом промежуткеесть хотя бы один корень данного уравнения()=0, поскольку на концах промежутка левая часть уравнения принимает значения разных знаков,аграфик ее сплошная линия, и, значит, в некоторой точкепромежутка он обязательно пересекает ось абсцисс»;«Полученноесоотношение можно условно записать в виде1∞=0. Это отражает тот факт,что,деля единицу на очень большое число,мы получили число очень маленькое,«почти нуль»и т.п.Ориентируясь на развитие интуитивного знания,следует систематически раскрывать «грубый»смысл обсуждаемых основных понятий. Более того,учитывая важную роль «свежих»впечатлений, желательно, чтобы сами определенияосновных понятий максимально способствовали появлению этого смысла. Рассмотрим,например, понятиепроизводной. Вприложениях оно выступает как скорость изменения одной величины по отношению к другой,либо как наклон (угловой коэффициент)элемента графиков функций. Стандартноежеопределение с помощью предела отношения приращения является лишь уточнением (впрочем,весьма существенным),формализациейэтого основного,«грубого» содержанияпонятия. Поэтому как при определении,так и в дальнейшем надо регулярно освещать, демонстрировать это содержание,стараясь внедрять его в интуицию.Следует иметь в виду,что в процессе обучения может развиться не только правильная, но ошибочнаяинтуиция. Так,до самого последнего времени у учащихся глубоко укоренилась ошибочное представление,что «некруглый»ответ (не извлекаются нацелокорни и т.п.) свидетельствует об ошибкев решении.Мы надеемся,что систематическое (начиная примерно с6 класса) применение микрокалькуляторовв школьной практике приведет к разрушению этого представления.Оценка ситуации.Важнейшими проявлениями продуктивной математической интуиции являются умение ориентироваться в новой незнакомой ситуации, способность предвидеть верные результаты, выбирать пути их получения, замечать явные ошибочные выводы. Такая продуктивная интуиция должна опираться на интуитивное видение соответствующих математических понятий и фактов.Навыки правильной предварительной оценки ситуации следует воспитывать при решении как условноприкладных (текстовых), так и чисто математических задач. При решении текстовой задачи желательно с максимальной ясностью представить ситуацию, как бы вообразив себя ее участником, прибегая к схематическим чертежам и неформальному анализу, сравнивая исходные данные задачи с хорошо известными значениями, проводя аналогии и так далее. Для развития продуктивной интуиции очень полезно, чтобы в процессе неформального обсуждения учащиеся пришли к некоторой оценке ожидаемого ответа –в виде неравенства( «более двух часов»), двусторонней оценки («от двух до пяти часов»), прикидке значения («часа три») или хотя бы его порядка («несколько часов»). Такие предварительные оценки у разных учеников могут быть различными, и после полученияточного решения важно выслушать соображения как тех, кто оказался близким к истинному результату, так и «неудачников». Пример: «Первый кран наполняет бассейн за 2 часа, второй –за 4 часа, за сколько часов наполниться бассейн, если оба крана открыты?» Сначала выясняем, что первый кран более мощный. Далее, без всяких выкладок, на основе здравого смысла заключаем, что, поскольку краны помогают друг другу, искомое время составит меньше двух часов. Несколько труднее, но все же не так уж сложно получить и оценку снизу: если бы второй кран был той же мощности, что и первый, то они вместе заполнили бы весь бассейн за 1 ч, значит, искомое время больше чем 1 час. Таким образом, до решения задачи мы получили гарантированную двустороннюю оценку ответа. Получив ответ, надо проверить, что он удовлетворяет этой оценке. Невнимание к подобным оценочным суждениям при обучении математике приводит к тому, что многие школьники (или студенты вуза), получая заведомо неверные ответы, которые даже самая грубая прикидка отбрасывает, спокойно их записывают как решение.Навык освоения ситуации весьма важен для построения математических моделей даже простейших реальных задач, не менее важен, чем формальные навыки решения задач.Предварительную оценку ситуации следует проводить при решении формальных задач.Прикидки.Оценка ситуации и прогноз ответа опираются на навык пользоваться прикидками. Они обычно осуществляются устно, в уме, поэтому требует твердых навыков устного счета. Приближенные прикидки проводят чаще всего с точностью до 12 верных цифр, порой даже до порядка величины. Пример: Пусть надо произвести прикидку значения ܽ=2,371∗72251,6+0,0976.Числитель приближенно равен 2б4∗7∗102≈17∗102. В знаменателе второе слагаемое на два порядка меньше первого, а потому второе слагаемое можно не учитывать. Значит, ܽ≈17∗1025∗10≈34.Отметим, что значение ܽ, подсчитанное на микрокалькуляторе и округленное по известным правилам, равно 33,0.Полезными для развития числовой интуиции являются задачи на оценку и нахождение целой части корней и логарифмов. Примеры типичных вопросов такого рода: «Какова масса стального шара диаметром 1 дм?», «Сколько человек может уместиться на баскетбольной площадке?».Рассмотрим простые правила округлений при прикидках. Если при подсчете произведения один из множителей округляется большую сторону, то второй желательно округлить в меньшую сторону, чтобы по возможности компенсировать первое округление. Пример: 3,5∗2,5надо округлять как 4∗4=8или 3∗3=9, но не 3∗2=6или 4∗3=12.Такое же правило действует и при сложении, а вот при вычитании и делении округление желательно производить в одну сторону. Необходимо иметь в виду резкую потерю точности при вычитании друг из друга близких приближенных значений, делающую порой непосредственную прикидку невозможной. Прикидка 12,11∗2,87−5,17∗1,22≈12∗3−5∗1≈1является грубо ошибочной (заменить 1,22 не на 1, а на 1,2). Точный подсчет дает после округления значение −4.Как при вычислении на микрокалькуляторе выяснить точность результата, если исходные данные были приближенными? Для этого имеются соответствующие правила. Однако часто бывает проще всего повторить вычисления, «пошатав» исходные данные в пределах их точности; при этом изменившийся результат укажет на недостоверные цифры, которые в ответе наверняка надо округлить. Если такое вычисление несложно или если оно осуществляется с помощью программирования, то его желательно повторить несколько раз.Систематическое применение подобных прикидок способствует воспитанию интуиции оценки величин. Это интуиция помогает правильно поставить задачу, отбросив малозначащие факторы, заметить ошибки.Навыки устных прикидок позволяют в ряде случаев быстро получать точные целочисленные решения несложных задач.Рассмотрим в качестве примера старинную задачу о стае гусей. «Летел гусь, а навстречу ему стая гусей. «Здравствуйте, сто гусей!» сказал он. «Нас не сто гусей, отвечает вожак стаи, если бы нас было еще столько, и ещё пол столько и еще четверть столько, да ты, гусь, с нами, то нас было бы сто». Сколько гусей было в стае?». Задачу можно решить с помощью уравнения. Но для развития арифметической интуиции полезнее путь прикидок. По смыслу задачи число гусей в стае кратно четырем и имеет порядок нескольких десятков. Попробуем значение =40получаем 40+40+20+10+1 –больше, чем 100; при =32–меньше, чем 100. Остается =36,и легко убедиться, что это значение подходит. Еще пример такого рода: пусть требуется вычислить ܽ=√175763, причём известно, чтоацелое число. Решение: прикидкой устанавливаем, что 20

интуитивная математика — с английского на русский

См. также в других словарях:

• ИНТУИЦИОНИЗМ — (от позднелат. intuitio, от лат. intueor пристально смотрю) направление в обосновании математики и логики, согласно которому конечным критерием приемлемости методов и результатов этих наук является наглядно содержательная интуиция. Вся математика …   Философская энциклопедия

• Интуиционизм — Интуиционизм  система философских и математических идей и методов, связанных с пониманием математики как совокупности «интуитивно убедительных» умственных построений. С точки зрения интуиционизма, основным критерием истинности… …   Википедия

• Интуиционистская логика — Интуиционизм  система философских и математических идей и методов, связанных с пониманием математики как совокупности «интуитивно убедительных» умственных построений. С точки зрения интуиционизма, основным критерием истинности математического… …   Википедия

• множеств теория —         МНОЖЕСТВ ТЕОРИЯ учение о множествах, зародившееся в середине 19 в. и изучающее свойства множеств произвольной природы. Создание М. т. было подготовлено работами математиков, ставивших целью разработку оснований анализа. Первые работы в… …   Энциклопедия эпистемологии и философии науки

• ЛОГИКА В РОССИИ — эволюция современной (математической) логики в России. Кон. 19 в. и нач. 20 в. знаменуют выход логики за рамки силлогистики и появление логиков новаторов, таких как П.С. Порецкий, М.В. Каринский, Л.В. Рутковский, СИ. Поварнин, и др. Казанский… …   Философская энциклопедия

• ТЕОРИЯ ПОЗНАНИЯ — Гносеология (от греч. gno sis знание, logos слово, понятие), Эпистемолог и я (от греч. episteme знание) раздел философии, исследующий природу человеческого познания, его источники и предпосылки, отношение знания к предмету познания, условия… …   Философская энциклопедия

• ИНТУИЦИОНИЗМ — совокупность философских и математич. идей и методов, рассматривающих математику как науку об умственных построениях. С точки зрения И., основным критерием истинности математич. суждения является интуитивная убедительность возможности построения… …   Математическая энциклопедия

• Кант Иммануил — Жизненный путь и сочинения Канта     Иммануил Кант родился в Кенигсберге (ныне Калининград) в Восточной Пруссии в 1724 г. Отец был шорником, а мать домохозяйкой, шестеро их детей не дожили до зрелого возраста. Кант всегда вспоминал родителей с… …   Западная философия от истоков до наших дней

• ИНТУИЦИОНИСТСКАЯ ЛОГИКА — одна из наиболее важных ветвей неклассической логики, имеющая своей филос. предпосылкой программу интуиционизма. Выдвигая на первый план математическую интуицию, интуиционисты не придавали большого значения систематизации логических правил.… …   Философская энциклопедия

• Парадигма — (Paradigm) Определение парадигмы, история возникновения парадигмы Информация об определении парадигмы, история возникновения парадигмы Содержание Содержание История возникновения Частные случаи (лингвистика) Управленческая парадигма Парадигма… …   Энциклопедия инвестора

• ЧИСЛО — Понятие числа в математике может относиться к объектам различной природы: натуральным числам, используемым при счете (положительным целым числам 1, 2, 3 и т.д.), числам, являющимся возможными результатами (идеализированных) измерений (это такие… …   Энциклопедия Кольера
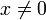