Примеры по арифметике
В математике арифметика является тем ее подразделом, в котором предметом изучения являются отношения, свойства чисел, а также они сами. Что касается происхождения названия этой дисциплины, то оно – греческое. Дело в том, что на языке эллинов само по себе слово «аритмос» означает в переводе на русский язык ни что иное, как «число».
Таким образом, арифметика представляет собой науку, которая изучает простейшие числа и те операции, которые над ними производятся. Во втором случае арифметика называется высшей. Кроме того, еще одно из очень важных задач арифметики является изучение свойств отдельных целых чисел.
Именно с ее теорией арифметика связана самым тесным образом, причем не только с ней, но также и с геометрией и алгеброй.
Предмет арифметики
Свойства чисел, их множества, а также действия над ними являются предметом арифметики. Кроме того, к нему зачастую также относят и изучение таких вопросов, как техника счета, умножение, деление, вычитание, вычисление квадратного корня, а также решение комплексных численных уравнений.
В принципе если рассмотреть арифметику с чисто математической точки зрения, то можно обнаружить, что она включает в себя целый ряд действий. К таковым, помимо обычного счета, относятся удвоение (то есть, увеличение в два раза даже без умножения), а также некоторые другие операции ( в том числе деление и умножение с остатком). Еще одной важной операцией, которая решается арифметикой, является поиск суммы и точное определение как геометрической, так и арифметической прогрессии.
Что касается рассмотрения степени сложности иерархии арифметики, то она имеет, по сути дела, несколько ступеней. Самыми низкими из них являются вычитание и сложение, чуть выше располагаются умножение и деление, а потом – такие действия, как извлечение корней и возведение в степень. Если говорить о тех возможностях, которые, что называется, прилагаются дополнительно, то к таковым относятся построение пропорций, вычисление процентов, а также многие другие операции, которые относятся к сфере практической и теоретической арифметики.
Раздел математики, называемый арифметикой, достаточно тесно связан с алгеброй. Предметом ее изучения является проведение операций, который не учитывают ни свойства, ни особенности чисел.
Арифметика в повседневной жизни
В повседневной жизни арифметика используется не просто очень часто, а практически постоянно. Без базовых арифметических навыков не может прожить ни один современный человек. В принципе, они прививаются людям еще тогда, когда они учатся в начальной школе. Впоследствии навыки, средства, приемы и техника элементарной арифметики становятся, по сути дела, нормой жизни, и даже не воспринимаются теми, кто ими пользуется, как некие отдельные возможности, позволяющие решать те или иные проблемы.
С бытовой точки зрения получается так, что к арифметическим операциям прибегают практически все люди, и практически постоянно. Они предполагают подсчет соотношения тех или иных величин (скажем, денежных единиц или их сумм), а также таких показателей, как скорость, промежутки времени, объем, площадь и пр. Необходимо отметить, что арифметика очень тесно связана с такими науками, как экономика и техника, а также с некоторыми другими, в которых активно используются арифметические вычисления.
Простой арифметический пример вызвал войну ответов в сети

Математика наука точная и разночтений не допускает. Но наш мир не так прост, как кажется и даже такая серьезная «дама» может подкинуть тему для серьезного спора. Посмотрите на этот простенький пример, который легко решить с самыми элементарными знаниями арифметики.

Ответ очевиден — 1. Именно так посчитало большинство пользователей сети.

Но не тут-то было — оказывается нашелся и другой вариант.



И тут понеслось — Сеть взорвалась, в дело пошли самые веские аргументы . Народ начал мериться авторитетом, уровнем образованности и просто «зуб давать».


В качестве рефери привлекли беспристрастную технику…




Попытка снять напряжение легкой шуткой не удалась…

Google-калькулятор принял одну из сторон

Наконец, в ход пошло правило PEMDAS

Все просто. В англоязычных странах действует правило PEMDAS, которое регулирует последовательность выполнения арифметических действий. Итак, первым делом выполняются действия в скобках (Р), затем — возведение в степень (Е), далее умножение и деление (MD) и сложение и вычитание (AS). Причем после раскрытия скобок все операции выполняются слева направо.

Вот так-то.
© Ribalych.ru
Двоичная арифметика
Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.
Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.
Таблица сложения, вычитания и умножения для двоичной системы счисления
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 — 0 = 0 | 0 ∙ 0 = 0 |
| 0 + 1= 1 | 1 — 0 = 1 | 0 ∙ 1 = 0 |
| 1 + 0 = 1 | 1 — 1 = 0 | 1 ∙ 0 = 0 |
| 1 + 1 = 10 | 10 — 1 = 1 | 1 ∙ 1 = 1 |
Сложение двоичных чисел
Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.
Пример: 1011,12 + 1010,112
Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример: 111,12 + 1112 + 101,12
При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 1002. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 1012. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.
Вычитание двоичных чисел
В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример: 10110,012 — 1001,12
Умножение и деление двоичных чисел

Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.
Пример: Перевести число 1011110112 в десятичную систему счисления.
Поскольку 1010 = 10102, запишем

Полученные остатки, 10012 = 910, =1112 = 710, 112 = 310. Искомое число 1011110112 = 37910.
Назад: Представление данных и архитектура ЭВМ
Предложения со словосочетанием АРИФМЕТИЧЕСКИЕ ПРИМЕРЫ
Выражение (1. 2) описывает условие обмена двух подразделений в случае расширенного воспроизводства в общем виде, без привлечения арифметических примеров из «Капитала». Необходимо приучить учеников давать развёрнутые объяснения при решении арифметических примеров и задач. Например, гимнастка может решать простые арифметические примеры, идя по бревну, ширина которого равна 10 см, в то же время человек, далёкий от спорта, вряд ли это сделает. Пропишите
 Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: вольнодумие — это что-то нейтральное, положительное или отрицательное?
Положительное
Отрицательное
Школьник-рационал может аккуратно решить подряд 20 арифметических примеров и не заметить, что в половине случаев вместо сложения от него требовалось произвести умножение. Задачи эти конкретны и абсолютно ясны; например, вам предложат решить квадратное уравнение или простенький арифметический пример на уровне пятого класса школы. В большинстве школ давно прошли те времена, когда уроки математики представляли собой решение бесконечных арифметических примеров, которые следовало выполнять в полной тишине по методикам сложения и умножения, разработанным сотни лет назад. Вообще, на порядок выполнения действий формулы влияют все её функции и операции, так как у каждой из них есть своя, вполне определённая очерёдность выполнения, которую можно сравнить с порядком действий в арифметических примерах, где умножение и деление выполняется в первую очередь, а сложение и вычитание — во вторую. Что же касается арифметических примеров, то «2 +2» и «9-5» представляют собою обозначение арифметических операций и в этом качестве являются именами называемых процессов как отдельных объектов познания. Например, я долго не мог составлять в столбики арифметические примеры. Один при письме не допускал грамматических ошибок, другой хорошо считал арифметические примеры. Для этого перед дегустацией половину участников заставили не думать о белом медведе, а второй дали решать несложные арифметические примеры. Он воспринимает окружающий мир, словно одновременно решает несколько трудных арифметических примеров. Я был голоден, но едва я проглотил первый кусок, как на меня посыпались арифметические примеры, которых хватило на всё время завтрака. И одного взгляда на моего мучителя, на его рыбьи глаза и разинутый рот, на рыжеватые волосы, вопросительно торчащие кверху, на жилет, распираемый арифметическими примерами, было достаточно, чтобы я решил назло ему ничего не рассказывать. Решить арифметический пример — тоже действие. Однако он не компонент арифметического примера для верующих христиан, а человек. Больному предлагают списать несколько простых слов или решить простые арифметические примеры. Представился и попросил её решить простой арифметический пример, но девушка сосредоточила всё внимание на вилке, на него даже не взглянула. Она с тихим ужасом взирала на колонки арифметических примеров.Неточные совпадения
То же самое можно пояснить на всяком другом примере: спрашиваю ли я об исторической дате какого-либо события, истина, которой я ищу, есть абсолютный синтез между датою и событием; решаю ли я какую-нибудь арифметическую задачу, опять-таки искомая истина выразится в виде синтеза того или другого понятия с тем или другим числом. Образцы арифметических записей учителя, его объяснения, направленные на раскрытие последовательности в решении примера, служат лучшими средствами обучения вычислениям.занимательная арифметика в картинках с ответами
Занимательные примеры на сложение и вычитание
Перед вами 7 заданий, которые можно использовать для короткого дополнительного занятия с первоклассником. Решать сейчас эти примеры в уме или на бумаге не обязательно.
Вы сможете выполнять интерактивные задания в персональном кабинете. А здесь мы просто показываем родителям и учителям примеры задач. Чтобы вы сразу поняли, что наконец-то нашли то, что искали 😉.
В магическом квадрате сумма чисел в любой горизонтали, вертикали и диагонали одинакова.
Определи недостающее число.
Расставь знаки арифметических действий между числами.
Определи, какой знак спрятался за кругом.
С ЛогикЛайк ребёнок не соскучится! И подружится с логикой и математикой.
Злобный вирус прячет одинаковые цифры за одинаковыми картинками.
Какие цифры спрятались за совой и попугаями?
5 математических уравнений, над которыми сейчас ломает голову весь интернет

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Ученые настаивают на том, что занятия математикой — это одна из лучших тренировок для нашего мозга. Интересно, что полезными могут быть не только сложные вычисления, но и простые головоломки, которые часто можно встретить в интернете.
Мы в AdMe.ru любим испытывать себя такими задачками, поэтому предлагаем и вам решить несколько уравнений, которые стали вирусными в последнее время.
1. В твиттере спорят из-за школьной задачки
Недавно хитом стало простое на первый взгляд уравнение. Спорить пользователи социальной сети начали из-за уточнения автора твита: «Это математический мем, который на самом деле смешной, а не глупый. Вы, вероятно, не поверите, но ответ — 5!»
Большинство людей считает, что правильный ответ — 120. Но профессора математики продолжают настаивать на том, что 230 — 220 × 0,5 = 5! Кто прав?
Нажмите на картинку, чтобы узнать ответ.
2. Еще одно уравнение, которое разделило интернет на 2 лагеря
Есть 2 распространенных ответа: 1 и 16. Даже калькуляторы запутались:
Вы на чьей стороне?
Нажмите на картинку, чтобы узнать ответ.
3. Тест на внимательность
В Гонконге эту задачку должны уметь решать ученики 1-го класса.
Нажмите на картинку, чтобы узнать ответ.
4. По какому принципу построены эти примеры?
Нажмите на картинку, чтобы узнать ответ.
Нажмите на картинку, чтобы узнать ответ.
Может, вы помните уравнения, которые еще больше запутают людей? Если да, поделитесь ими с другими читателями. Кто знает, может, ваша задачка станет новым хитом интернета.
Понятие арифметики. Арифметические действия | matematicus.ru
Арифметика (от греч. .«аритмос» или «арифмос» — число ) — это наука о числах и входит в раздел математики. В арифметике изучаются простейшие свойства чисел и правила вычислений.
Простым числом называют натуральное число, которое имеет два делителя — единицу и само себя. Например, 5, 7, 11, 13. Таблица простых чисел.
Составным числом называют натуральное число, которое имеет более двух делителей. Например, 9, 10, 16, 100. Любое составное число можно представить единственным способом в виде произведения простых множителей. Например, 20 = 2·2·5.
2; 4; 6; 8; 10; 12 … – четные числа.
1; 3; 5; 7; 9; 11 … – нечетные числа.
1.Сложение
a + b = c
a и b — слагаемые, c — сумма.
2. Вычитание
a — b = c
a — уменьшаемое,
b — вычитаемое,
c — разность.
3. Умножение
a · b = c
a — множимое,
b — множитель,
c — произведение.
Замечание
Если множимое и множитель поменять местами, то произведение останется тем же. Также множитель и множимое называются «сомножителями».
4. Деление
a : b = c
a — делимое,
b — делитель,
c — частное.
Если делимое не делится нацело на делитель, то такое деление называют деление с остатком.
5. Возведение в степень.
ab = c
a — основание степени, b — показатель степени, c — степень; 34 = 3*3*3*3.
Замечание
Вторая степень называется квадратом, а третья степень — кубом.
6. Извлечение корня.
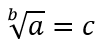
a — подкоренное число,
b — показатель корня,
c — корень
Замечание
Корень второй степени называется квадратным, а корень третьей степени — кубичным.
Замечание
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно являются обратными действиями.
Сложение.
a + 0 = a
Вычитание.
a — 0 = a
Умножение.
a · 0 = a
Деление.
0 : a = a
Замечание
Частное от деления нуля на нуль неопределенно. В подобных случаях рассматривают «раскрытие неопределенности 0:0»
Замечание
Частное от деления любого числа, отличного от нуля, на нуль не определенно или не существует. Также записывают как бесконечно большое число, т.е. a:0 = ∞
Первое арифметическое действие всегда выполняется в скобках слева направо.
Если выражение без скобок, то сначала выполняются действия умножения или деления, затем сложения или вычитания.

Арифметические действия с дробями см. здесь
