Арифметика что это – Ментальная арифметика – что это такое? Как научиться ментальной арифметике в домашних условиях?

АРИФМЕТИКА — это… Что такое АРИФМЕТИКА?

— область знаний о числах и операциях в числовых множествах. Говоря об А., имеют в виду рассмотрение вопросов о происхождении и развитии понятия числа, приемы и средства вычислений, исследование операций с числами различной природы, анализ аксиоматич. структуры числовых множеств, свойства чисел. Когда делается упор на логич. анализе понятия числа, то иногда употребляют термин теоретическая арифметика. А. тесно связана с алгеброй, в к-рой, в частности, изучаются свойства операций над числами. Свойства же самих целых чисел составляют предмет теории чисел (см. Элементарная теория чисел, Чисел теория).

Термин «А.» иногда употребляют и тогда, когда имеют дело с операциями над объектами самой различной природы: «А. матриц», «А. квадратичных форм» и т. д.

Культура счета возникла и развивалась задолго до создания дошедших до нас письменных памятников. Наиболее древними письменными математич. памятниками являются кахунские папирусы и знаменитый папирус Ринда, относящийся приблизительно к 2000 до н. э. Аддитивная иероглифич. система

счисления позволяла египтянам сравнительно просто производить только операции сложения и вычитания натуральных чисел.

Умножение выполнялось с помощью удвоения, т. е. множитель разбивался на сумму степеней двойки, производилось умножение на отдельные слагаемые, а затем компоненты складывались. Действия с дробями египтяне сводили к операциям саликвотными дробям п, т. е. с дробями вида -. Более сложные дроби разбивались с помощью таблиц на сумму алпквотных дробей. Деление осуществлялось вычитанием из делимого чисел, получаемых в процессе последовательного удвоения делителя. Громоздкая шестидесятичная система счисления вавилонян вызывала большие трудности при выполнении арифметич. операций. До нас дошли многочисленные таблицы, с помощью к-рых вавилоняне выполняли умножение и деление.

А. у греков — изучение свойств чисел; они не относили к ней практику вычислений. Вопросы, связанные с техникой операций над числами, т. е. способы вычислений, составляли особую науку, наз. логистикой. Такое разделение от греков перешло в средневековую Европу. Только в эпоху Возрождения общим назв. А. стали объединять как начатки теории чисел, так и практику вычислений. Греческая математика резко разграничивала понятия числа и величины. Греческие математики называли числами только те числа, к-рые теперь наз.

натуральными числами, и различали такие разнородные, по их представлениям, понятия, как числа п гео-метрич. величины. Специальные греческие сочинения по логистике до нас не дошли: все же известно, что греки применяли способ умножения, близкий к современному. Алфавитная система нумерации сильно усложняла операции над числами. Греки практиковали вычисления с обыкновенными дробями, однако дроби не рассматривались как- числа, а только как отношения натуральных чисел.

7 -9-ю книги «Начал» Евклид (3 в. до н. э.) посвятил целиком А. в античном. алгоритм отыскания

наибольшего общего делителя (см. Евклида алгоритм), теоремы о простых числах. Евклид обосновывает коммутативность умножения, а также дистрибутивность этой операции относительно сложения. Рассматривается теория пропорций, т. е., по существу, теория дробей. В других книгах в геометрич. форме излагается общая теория отношений величин, к-рую можно рассматривать как зачатки теории действительных чисел.

8 дошедших до нас рукописях Диофанта (вероятно, 3 в.) можно найти действия со степенями, показатели к-рых не превосходят шести, и нек-рые приемы операций с вычитаемыми. В неявной форме это операции с отрицательными числами. Сформулированные Диофантом правила применялись им только к рациональным числам.

Китайские математики во 2 в. оперировали с дробями и отрицательными числами. Несколько позже ими рассматривались методы извлечения квадратных п кубич. корней, приближенные значения к-рых выражались в виде

десятичных дробей. Применявшиеся китайскими математиками для решения арифметич. задач правила, в частности правило двух ложных положений, вошли во многие руководства по А. сначала у арабов, а затем и в Европе. О начальном периоде арифметич. культуры в Индии не имеется достаточно данных. Простейшие дроби употреблялись в Индии задолго до нашей эры. Ныне общепринятая десятичная система счисления индийского происхождения. Начиная с 5 в. имеются датированные письменные источники и они показывают высокую арифметич. культуру Индии в ту эпоху. Индийские математики оперировали с целыми и дробными числами методами, близкими к современным. Решались многие задачи на пропорции, тройное правило и проводились процентные вычисления. С 7 в. начали рассматриваться отрицательные числа. В сочинениях Бхаскары II «Венец науки» (12 в.) приводятся правила умножения и деления отрицательных чисел.

Индийская математика оказала решающее влияние на развитие арифметич. знаний у арабов. Написанный в 9 в. Мухаммедом аль-Хорезмп трактат по А. способствовал повсеместному распространению индийской десятичной системы записи чисел и способов сложения, вычитания, умножения, деления и извлечения квадратного корня.

У многих древних народов первоначальные приемы счета на пальцах заменяются вычислениями на абаке. Абак менял свою форму, но принцип оставался один и тот же — разграфленные колонны или к.-л. другим образом отведенные места для поразрядной отметки чисел. У греков абак употреблялся задолго до нашей эры. Абак (суан-пан) у китайцев по форме близок к нашим русским счетам, представляющим собой также разновидность абака.

В то время как теоретико-числовые исследования в Европе возникли на базе греческой математики, в первую очередь трудов Евклида п Диофанта, совершенно иначе обстоит дело с техникой вычислений. Развитие А. в Европе связано с распространением индийской десятичной позиционной системы и

арабских цифр. Техника арифметич. операций заимствована из Индии не непосредственно, а в результате ознакомления с трудами Мухаммеда аль-Хорезми и других арабских математиков.

В средние века широко применялся абак. Он стал даже синонимом слова А., так что Леонардо Ппзанский (Leonardo Pisano, 13 в») назвал свой трактат по А. «Книга абака». В этой книге изложены заимствованные иа арабских источников приемы вычисления, однако сделаны и существенные усовершенствования. Напр., при сложении дробей используется наименьшее общее кратное знаменателей, а проверка действий производится не только, как это делали индийцы с помощью девятки, но и с использованием нек-рых других модулей, Рассматриваются задачи на тройное правило, правиле товарищества, на смешение величин, задачи, в к-рыз фигурируют рекуррентные последовательности, арифметические прогрессии и геометрические прогрессии. В Европе первые шаги в направлении применения десятичных дробей были сделаны в 15 в., но широкое распространенпе они получили только в 16 в. после выхода сочинений С. Стевина (S. Stevin).

В 15-16 вв., да и позже, предлагались разные схемы для умножения и деления многозначных чисел. Эти схемы отличаются друг от друга, в сущности, только характером записи промежуточных вычислений. Общепринятый в настоящее время способ умножения ввел А. Ризе (A. Riese, 16 в.).

Отрицательные числа появляются в Европе впервые у Леонардо, к-рый трактовал их в форме долга. Операции с отрицательными числами систематизируются М. Штифелем (М. Stiefel, 16 в.). Такие числа он наз. «фиктивными». В 18 в. еще рассматривались доказательства правил операций с отрицательными числами и только критич. мышление 2-й пол. 19 в. положило конец серьезному восприятию таких работ.

Арифметич. действия над иррациональными числами до 15-16 вв. в Европе ограничивались квадратными корнями. Все же Леонардо рассматривал вопрос о приближенном вычислении не только квадратных, но и кубич. корней. С. Даль Ферро (S. Dal Ferro, конец 15 в.-начало 16 в.) и Н. Тарталья (N. Tartaglia, 16 в.) при решении уравнения 3-й степени стали употреблять кубич. корни. Общая трактовка операций с действительными числами отсутствовала. Понятие действительного числа входило в математпч. обиход только постепенно в связи с развитием аналитич. еометрии и математич. анализа.

Вплоть до 18 в. обоснование операций над иррациональными числами ограничивалось величинами выражаемыми в радикалах. При рассмотрении квадратных уравнений математики разных эпох, начиная с индийских математиков, встречались с комплексными величинами. Однако мнимые решения отбрасывались как несуществующие. А. комплексных чисел начинается с работ Р. Бомбеллн (R. Bombelli, 16 в.), давшего формальные правила арифметич. действий над такими числами. Но и в 17 в. операции над комилексными числами производили по аналогии с операциями над действительными числами, что часто приводило к ошибкам. Только в 18 в. формулы Муавра и Эйлера обеспечили возможность четкого построения А. комплексных чисел.

Идея введения логарифмов восходит к Архимеду (3 в. до н. э.), к-рый сравнивал члены геометрич. и арифметич. прогрессий. М. Штифель (М. Stiefel, 16 в.) продолжил сравниваемые прогрессии влево, добавив отрицательные степени. Он показал связь между операциями над этими рядами, дав, таким образом, основную идею логарифмов. Логарифмирование и использование этой операции для вычислений начали применять в 1-й пол. 17 п. после работ Дж. Непера (J. Napier) и и. Бюрги (J. Burgi).

В 17 в. В. Шиккард (W. Schickard) и Б. Паскаль (В. Pascal) создали независимо друг от друга вычислительные машины — прототипы современных арифмометров. Но широкое практич. применение счетные машины получили только в 19 в. В сер. 20 в. распространяются быстродействующие электронные вычислительные машины. В связи с этим актуальными становятся задачи отыскания алгоритмов, позволяющих выполнять арифметич. действия с наименьшим числом элементарных операций.

Чтобы обосновать какую-нибудь теорию, со времени Евклида считалось достаточным выделить в ней небольшое число ясных простейших первичных начал и убедиться, что все основные положения данной теории можно вывести из них чисто логически. Подразумевалось, что связь этих начал с действительным миром должна быть доступной непосредственному восприятию.

В 19 в. был открыт метод моделей для обоснования математич. теорий. Необходимость этого метода была обусловлена тем, что в математике стали рассматриваться объекты и теории, для к-рых не удавалось найти реального истолкования. непротиворечивость одной математич. теории к непротиворечивости другой. Так, в предположении, что непротиворечива евклидова геометрия, была доказана непротиворечивость геометрии Лобачевского, а непротиворечивость евклидовой геометрии была сведена к непротиворечивости А. действительных чисел.

К концу 19 в. обоснование А. казалось завершенным. Р. Дедекинд (Н. Dedekind) и, независимо от него, Дж. Пеано (G. Реапо) указали систему аксиом А. натуральных чисел, из к-рой можно вывести все известные положения этой науки. К. Вейерштрасс (К. Weierstrass) предложил в качестве моделей для целых и положительных рациональных чисел классы пар натуральных чисел. Геометрич. истолкование комплексных чисел, открытое Ж. Арганом (J. Argand), К. Весселем (С. Wes-sel) и К. Ф. Гауссом (К. F. Gauss), по существу является моделью для теории комплексных чисел в рамках теории действительных чисел. И, наконец, теоретико-множественный подход позволил Р. Дедекинду, Г. Кантору (G. Cantor) и К. Вейерштрассу построить теории действительных чисел.

Но после того, как стали известны парадоксы в теории множеств, возник вопрос: как обосновать А. натуральных чисел и действительных чисел? Есть ли гарантия, что парадоксы не будут обнаружены и в этих разделах математики? Непосредственное восприятие не позволяет сделать заключение ни о бесконечной протяженности Вселенной, ни о бесконечной делимости вещества. Поэтому представления о бесконечности множества натуральных чисел и о непрерывности числовой прямой нельзя рассматривать как непосредственно связанные с физическим миром. С другой стороны, для А. натуральных чисел нет более простой модели, чем сама эта теория, а при построении моделей для теории действительных чисел существенным образом используется аппарат теории множеств, в надежности к-рого появились основания усомниться.

Какими должны быть способы и средства рассуждений, на основании к-рых, не прибегая к построению модели, непосредственно можно убедиться, что в данной теории никогда не возникнет противоречий, что на основании аксиом данной теории нельзя с помощью цепочки логич. умозаключений получить результаты, противоречащие друг другу?

Д. Гильберт (D. Hilbert) считал, что парадоксы в теории множеств возникают вследствие того, что безотказно работающие в области конечных систем объектов способы рассуждений без должных оснований применяются к бесконечным совокупностям. Но этого можно избежать, если рассматривать употребляемые символы как объекты нек-рой новой теории, а логич. умозаключения выражать с помощью формального процесса. В таком случае любое высказывание теории представляется в виде формулы, составленной из конечного множества символов, а доказательство — в виде конечной цепочки формул, образованной по определенным правилам из формул, наз. аксиомами. Тогда, по мысли Д. Гильберта, появится возможность оперирования с бесконечным заменить оперированием с конечным и получить надежный способ установления непротиворечивости любой теории. Д. Гильберт надеялся, что на этом пути будет в первую очередь найдено положительное решение проблемы непротиворечивости А. натуральных чисел и, более того, будет показано, что присоединение к формулам А. любой недоказуемой формулы теории чисел превращает эту систему аксиом в противоречивую систему.

Но эти надежды не оправдались. В 1931 К. Гёдель (К. Godel) доказал неполноту арифметики формальной. Более того, оказывается, что для всякой непротиворечивой формальной системы, содержащей аксиомы А., можно дать явное описание нек-рой замкнутой формулы итакой, что ни сама формула и, ни ее отрицание не выводимы в этой формальной системе.

Воспользовавшись этим результатом, можно доказать существование неизоморфных моделей формальной А. Вместе стем система Пеано аксиом категорична. Как объяснить это? Система аксиом Пеано содержит аксиому индукции: каждое натуральное число обладает нек-рым свойством Р, если 1 обладает этим свойством и вместе с каждым натуральным числом п, обладающим свойством Р, натуральное число n+l также обладает свойством Р. В этой аксиоме за Рможет быть принято любое мыслимое свойство натуральных чисел. В соответствующей аксиоме формальной А. за Рможет быть принято лишь такое свойство натуральных чисел, к-рое выразимо средствами данного формализма. Различие между этими аксиомами незаметно, пока речь идет о теоремах элементарной теории чисел, и весьма существенно, когда выясняются свойства формальной теории. К. Гёдель показал также, что в непротиворечивой формальной системе, включающей формальную А., содержится формула, выражающая ее непротиворечивость, и что эта формула недоказуема в этой системе. Следовательно, непротиворечивость такой формальной системы может быть обоснована только средствами более сильными, чем те, к-рые формализованы в данной системе.

В 1936 Г. Генцен (G. Gentzen) получил доказательство непротиворечивости формальной А., использующее трансфннитную индукцию до трансфинитного числа 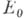. Естественно возникает вопрос о непротиворечивости тех средств, к-рые при этом были использованы. В связи с характером используемых средств рассматривались п другие подходы к проблеме непротиворечивости А. натуральных чисел.

Попытки преодоления трудностей, связанных с обоснованием теории действительных чисел, послужили одним из источников развития конструктивного направления в математике.

Лит.:[1] История математики, т. 1-3, М., 1970-72; [2] Ван дер Варден Б. Л., Пробуждающаяся наука, пер. с голл., М., 1959; [3] Клини С. К., Математическая логика, пер. с англ., М., 1973; [4] Гильберт Д., Основания геометрии, пер. с нем., М.-Л., 1948, с. 315-99; [5] Энциклопедия элементарной математики, кн. 1 — Арифметика, М.-Л., 1951; (6] Молодший В. Н.. Основы учения о числе в XVIII и начале XIX века, М., 1963; [7] Нечаев В. И., Числовые системы, М., 1975. А. А. Бухштаб, В. И. Нечаев.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.

Простая арифметика

Арифметикой называется тот раздел математики, предметом изучения которого являются числа, их свойства и отношения.

Ее название имеет греческое происхождение: на языке древней Эллады слово «аритмос» (его еще произносят как «арифмос») означает «число».

Арифметика изучает правила вычислений и простейшие свойства чисел. В том ее разделе, который называется теория чисел (или высшая арифметика), изучаются свойства отдельных целых чисел.

Арифметика самым тесным образом связана с теорией чисел, алгеброй и геометрией, и является одной из главных математических наук, а также самой древней из них.

Основными предметами арифметики являются действия над числами, их свойства, а также числовые множества. Кроме того, в арифметике изучаются такие вопросы, как происхождение и развитие понятия чисел, измерения и техника счета.

Действия над числами, являющиеся предметом изучения арифметики, – это сложение, вычитание, деление и умножение. К ним также можно отнести и такие операции, как извлечение корня, возведение в степень и решение различных численных уравнений.

Кроме того, исторически сложилось так, что к арифметическим действиям относят, помимо умножения, удвоение; помимо деления, деление с остатком и на два; счет; вычисление суммы геометрической и арифметической прогрессий. При этом все арифметические действия имеют собственную иерархию, в которой высшую ступень занимает извлечение корней и возведение в степень, более низкую – умножение и деление, и далее – сложение и вычитание.

Следует заметить, что те измерения и математические расчеты, которые находят широкое практическое применение (например, проценты, пропорции и т.п.) относятся к так называемой низшей арифметике, а понятие числа и его логический анализ – к арифметике теоретической.

Арифметика находится в очень тесной связи с алгеброй, основным предметом изучения которой являются различные операции с числами, не учитывающие их свойства и особенности. При этом извлечение корней и возведение в степень представляют собой техническую часть алгебры.

Поскольку в повседневной жизни арифметика используется практически повсеместно, то определенные познания в этой науке необходимы абсолютно всем. На протяжении жизни такие операции, как счет, вычисление объемов, площадей, скорости, временных промежутков и протяженностей приходится выполнять очень часто.

Для освоения любой профессии необходимо владеть основными арифметическими знаниями, и особенно это касается тех специальностей, которые связаны с экономикой, техникой и естественными науками.

Что такое арифметика? Основная теорема арифметики. Двоичная арифметика

Что такое арифметика? Когда человечество начало использовать числа и работать с ними? Куда уходят корни таких обыденных понятий, как числа, дроби, вычитание, сложение и умножение, которые человек сделал неотделимой частью своей жизни и мировоззрения? Древнегреческие умы восхищались такими науками, как математика, арифметика и геометрия, как прекраснейшими симфониями человеческой логики.

Возможно, арифметика не так глубока, как другие науки, но что было бы с ними, забудь человек элементарную таблицу умножения? Привычное нам логическое мышление, использующие цифры, дроби и другие инструменты, нелегко давалось людям и долгое время было недоступно для наших предков. Фактически до развития арифметики ни одна область человеческого знания не была по-настоящему научной.

Арифметика — это азбука математики

Арифметика – это наука о числах, с которой любой человек начинает знакомство с увлекательным миром математики. Как говорил М. В. Ломоносов, арифметика – это врата учености, открывающие нам путь к миропознанию. А ведь он прав, разве познание мира можно отделить от знания цифр и букв, математики и речи? Возможно, в былые времена, но не в современном мире, где бурное развитие науки и техники диктует свои законы.

Слово «арифметика» (греч. «арифмос») греческого происхождения, обозначает «число». Она изучает число и все что может быть с ними связано. Это мир чисел: различные действия над числами, числовые правила, решение задач, которые связаны с умножением, вычитанием и т. д.

Общепринято считать, что арифметика является начальной ступенькой математики и твердой основой для более сложных ее разделов, таких, как алгебра, матанализ, высшая математика и т. д.

Основной объект арифметики

Основа арифметики – это целое число, свойства и закономерности которого рассматриваются в высшей арифметике или теории чисел. По сути, от того, насколько верный подход взят в рассмотрении такого небольшого блока, как натуральное число, зависит прочность всего здания – математики.

Поэтому на вопрос о том, что такое арифметика, можно ответить просто: это наука о числах. Да, о привычной семерке, девятке и всем этом разнообразном сообществе. И подобно тому, как и хороших, и самых посредственных стихов не напишешь без элементарной азбуки, без арифметики не решить даже элементарной задачи. Вот почему все науки продвинулись только после развития арифметики и математики, будучи до этого всего лишь набором предположений.

Арифметика — наука-фантом

Что такое арифметика — натуральная наука или фантом? На самом деле, как рассуждали древнегреческие философы, ни чисел, ни фигур в реальности не существует. Это всего лишь фантом, который создается в человеческом мышлении при рассматривании окружающей среды с ее процессами. В самом деле, что такое число? Нигде вокруг мы не видим ничего подобного, что можно было бы назвать числом, скорее, число — это способ человеческого разума изучать мир. А может быть, это изучение нас самих изнутри? Об этом спорят философы много веков подряд, поэтому дать исчерпывающий ответ мы не беремся. Так или иначе, арифметике удалось настолько прочно занять свои позиции, что в современном мире никто не может считаться социально адаптированным без знания ее основ.

Как появилось натуральное число

Конечно, основной объект, которым оперирует арифметика, – натуральное число, такое, как 1, 2, 3, 4, …, 152… и т.д. Арифметика натуральных чисел является результатом счета обычных предметов, например, коров на лугу. Все-таки определение «много» или «мало» когда-то перестало устраивать людей, и пришлось изобретать более совершенные техники счета.

Но настоящий прорыв случился, когда человеческая мысль дошла до того, что можно одним и тем же числом «два» обозначить и 2 килограмма, и 2 кирпича, и 2 детали. Дело в том, что нужно абстрагироваться от форм, свойств и смысла предметов, тогда можно производить некоторые действия с этими предметами в виде натуральных чисел. Так родилась арифметика чисел, которая дальше развивалась и ширилась, занимая все большие позиции в жизни общества.

Такие углубленные понятия числа, как ноль и отрицательное число, дроби, обозначения чисел цифрами и другими способами, имеют богатейшую и интереснейшую историю развития.

Арифметика и практичные египтяне

Два древнейших спутника человека в исследовании окружающего мира и решении бытовых задач – это арифметика и геометрия.

Считается, что история арифметики берет свое начало на Древнем Востоке: в Индии, Египте, Вавилоне и Китае. Так, папирус Ринда египетского происхождения (назван так, поскольку принадлежал одноименному владельцу), датируемый XX в. до н.э, кроме других ценных данных содержит разложение одной дроби на сумму дробей с разными знаменателями и числителем, равным единице.

Например: 2/73=1/60+1/219+1/292+1/365.

Но в чем смысл такого сложного разложения? Дело в том, что египетский подход не терпел абстрагированных размышлений о числах, наоборот, вычисления производились только с практической целью. То есть египтянин станет заниматься таким делом, как расчеты, исключительно для того, чтобы построить гробницу, например. Нужно было высчитать длину ребра сооружения, и это заставляло садиться человека за папирус. Как видно, египетский прогресс в расчетах был вызван, скорее массовым, строительством, нежели любовью к науке.

По этой причине расчеты, найденные на папирусах, нельзя назвать размышлениями на тему дробей. Скорее всего, это практическая заготовка, которая помогала в дальнейшем решать задачи с дробями. Древние египтяне, не знавшие таблицы умножения, производили довольно длинные вычисления, разложенные на множество подзадач. Возможно, это одна из таковых подзадач. Нетрудно заметить, что расчеты с такими заготовками весьма трудоемки и малоперспективны. Может быть, по этой причине мы не видим большого вклада Древнего Египта в развитие математики.

Древняя Греция и философская арифметика

Многие знания Древнего Востока были успешно освоены древними греками, известными любителями отвлеченных, абстрактных и философских размышлений. Практика их интересовала не меньше, но лучших теоретиков и мыслителей найти сложно. Это пошло на пользу науке, поскольку в арифметику невозможно углубиться, не разорвав ее с реальностью. Конечно, можно умножать 10 коров и 100 литров молока, но далеко продвинуться не удастся.

Мыслящие глубоко греки оставили значительный след в истории, и их труды дошли до нас:

• Евклид и «Начала».
• Пифагор.
• Архимед.
• Эратосфен.
• Зенон.
• Анаксагор.

И, конечно, превращающие все в философию греки, а особенно продолжатели дела Пифагора, настолько были увлечены числами, что считали их таинством гармонии мира. Числа настолько были изучены и исследованы, что некоторым из них и их парам приписывали особые свойства. Например:

• Совершенные числа — те, которые равны сумме всех своих делителей, кроме самого числа (6=1+2+3).
• Дружественные числа — это такие числа, одно из которых равно сумме всех делителей второго, и наоборот (пифагорейцы знали только одну такую пару: 220 и 284).

Греки, считавшие, что науку нужно любить, а не быть с ней ради выгоды, достигли больших успехов, исследуя, играя и складывая числа. Нужно отметить, что не все их изыскания нашли широкое применение, некоторые из них остались лишь «для красоты».

Восточные мыслители Средневековья

Точно так же и в Средние века арифметика своим развитием обязана восточным современникам. Индийцы передали нам цифры, которые мы активно используем, такое понятие как «нуль», и позиционный вариант системы исчисления, привычный современному восприятию. От Аль-каши, который в 15 веке работал в Самарканде, мы унаследовали десятичные дроби, без которых трудно представить современную арифметику.

Во многом знакомство Европы с достижениями Востока стало возможно благодаря труду итальянского ученого Леонардо Фибоначчи, который написал произведение «Книга абака», знакомящее с восточными новшествами. Оно стало краеугольным камнем развития алгебры и арифметики, исследовательской и научной деятельности в Европе.

Российская арифметика

И, наконец, арифметика, нашедшая свое место и укоренившаяся в Европе, стала распространяться и на русские земли. Первая русская арифметика вышла в 1703 году – это была книга об арифметике Леонтия Магницкого. Долгое время она оставалась единственным учебным руководством по математике. Она содержит начальные моменты алгебры и геометрии. Цифры, которые использовал в примерах первый в России учебник арифметики, арабские. Хотя арабские цифры встречались и ранее, на гравюрах, датирующихся 17 веком.

Сама книга украшена изображениями Архимеда и Пифагора, а на первом листе — образ арифметики в виде женщины. Она сидит на престоле, под ней написано на иврите слово, обозначающее имя Бога, а на ступенях, которые ведут к престолу, начертаны слова «деление», «умножение», «сложение» и т. д. Можно только представить, какое значение предавали таким истинам, которые сейчас считаются обыденным явлением.

Учебник из 600 страниц описывает как основы вроде таблицы сложения и умножения, так и приложения к навигационным наукам.

Не удивительно, что автор выбрал изображения греческих мыслителей для своей книги, ведь он и сам был пленен красотой арифметики, говоря: «Арифметика есть числительница, есть художество честное, независтное… ». Такой подход к арифметике вполне обоснован, ведь именно ее повсеместное внедрение можно считать началом бурного развития научной мысли в России и общего образования.

Непростые простые числа

Простое число – это такое натуральное число, которое имеет только 2 положительных делителя: 1 и само себя. Все остальные числа, не считая 1, называют составными. Примеры простых чисел: 2, 3, 5, 7, 11, и все другие, которые не имеют прочих делителей, кроме числа 1 и себя самого.

Что же касается числа 1, то оно на особом счету – существует уговор, что его нужно считать ни простым, ни составным. Простое на первый взгляд простое число таит множество неразгаданных тайн внутри себя.

Теорема Евклида говорит, что простых чисел бесконечное множество, а Эратосфен придумал специальное арифметическое «решето», которое отсеивает непростые числа, оставляя только простые.

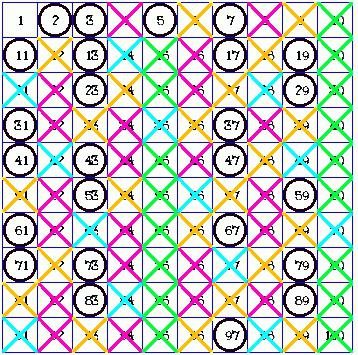
Ее суть в том чтобы подчеркивать первое невычеркнутое число, а в последующем вычеркивать те, которые ему кратны. Многократно повторяем эту процедуру — и получаем таблицу простых чисел.

Основная теорема арифметики

Среди наблюдений о простых числах нужно особым образом упомянуть основную теорему арифметики.

Основная теорема арифметики гласит, что любое целое число, большее 1, либо является простым, либо его можно разложить на произведение простых чисел с точностью до порядка следования сомножителей, причем единственным образом.

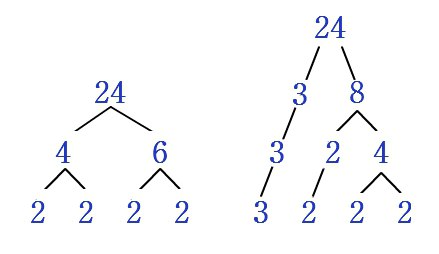
Основная теорема арифметики доказывается достаточно громоздко, да и понимание ее уже не похоже на простейшие основы.

На первый взгляд простые числа — элементарное понятие, однако это не так. Физика также некогда считала атом элементарным, пока не нашла внутри него целую вселенную. Простым числам посвящен прекрасный рассказ математика Дона Цагира «Первые пятьдесят миллионов простых чисел».

От «трех яблочек» до дедуктивных законов

Что поистине можно назвать армированным фундаментом всей науки – это законы арифметики. Еще в детстве все сталкиваются с арифметикой, изучая количество ножек и ручек у кукол, количество кубиков, яблочек и т. д. Так мы изучаем арифметику, которая дальше переходит в более сложные правила.

Вся наша жизнь знакомит нас с правилами арифметики, которые стали для простого человека наиболее полезными из всего, что дает наука. Изучение чисел — это «арифметика-малышка», которая знакомит человека с миром чисел в виде цифр еще в раннем детстве.

Высшая арифметика — дедуктивная наука, которая изучает законы арифметики. Большинство из них нам известно, хотя, возможно, мы и не знаем их точных формулировок.

Закон сложения и умножения

Два любых натуральных числа a и b могут быть выражены в виде суммы a+b, которая также будет числом натуральным. Касательно сложения действуют следующие законы:

• Коммутативный, который говорит, что от перестановки слагаемых местами сумма не изменяется, или a+b= b+a.
• Ассоциативный, который говорит, что сумма не зависит от способа группировки слагаемых местами, или a+(b+c)= (a+ b)+ c.

Правила арифметики, такие, как сложение, — одни из элементарных, но их используют все науки, не говоря уже о повседневной жизни.

Два любых натуральных числа a и b могут быть выражены в произведении a*b или a*b, которое также является числом натуральным. К произведению применимы те же коммутативные и ассоциативные законы, что и к сложению:

• a*b= b* a;
• a*(b*c)= (a* b)* c.

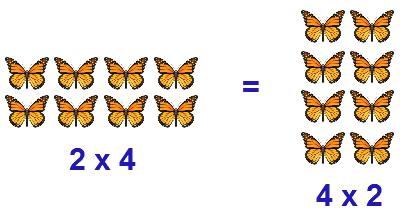
Интересно, что существует закон, который объединяет сложение и умножение, называемый также распределительным, или дистрибутивным законом:

a(b+c)= ab+ac

Этот закон фактически учит нас работать со скобками, раскрывая их, тем самым мы можем работать уже с более сложными формулами. Это именно те законы, которые будут вести нас по причудливому и непростому миру алгебры.

Закон арифметического порядка

Закон порядка человеческая логика использует каждый день, сверяя часы и считая купюры. И, тем не менее, и его нужно оформить в виде конкретных формулировок.

Если мы имеем два натуральных числа a и b, то возможны следующие варианты:

• a равно b, или a=b;
• a меньше b, или a < b;
• a больше b, или a > b.

Из трех вариантов справедливым может быть только один. Основной закон, который управляет порядком, говорит: если a < b и b < c, то a< c.

Существуют также и законы, связывающие порядок с действиями умножения и сложения: если a< b, то a + c < b+c и ac< bc.

Законы арифметики учат нас работать с числами, знаками и скобками, превращая все в стройную симфонию чисел.

Позиционные и непозиционные системы исчисления

Можно сказать, что числа – это математический язык, от удобства которого зависит многое. Существует множество систем исчисления, которые, как и алфавиты разных языков, отличаются между собой.

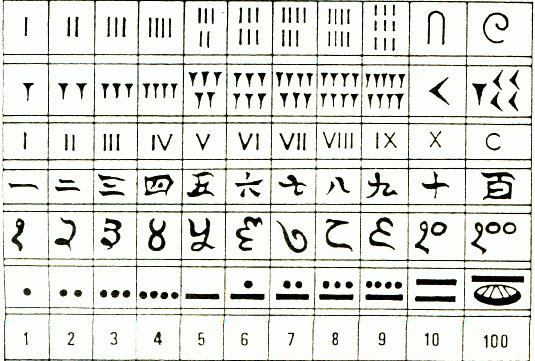
Рассмотрим системы счисления с точки зрения влияния позиции на количественное значение цифры на этой позиции. Так, например, римская система является непозиционной, где каждое число кодируется определенным набором специальных символов: I/ V/ X/L/ C/ D/ M. Они равны, соответственно, числам 1/ 5/10/50/100/500/1000. В такой системе цифра не изменяет своего количественного определения в зависимости от того, на какой она стоит позиции: первой, второй и т. д. Чтобы получить другие числа, нужно сложить базовые. Например:

Более привычная для нас система счисления с использованием арабских цифр является позиционной. В такой системе разряд числа определяет количество цифр, например, трехразрядные числа: 333, 567 и т.д. Вес любого разряда зависит от позиции, на которой находится та или иная цифра, например цифра 8 на второй позиции имеет значение 80. Это характерно для десятичной системы, существуют и другие позиционные системы, например двоичная.

Двоичная арифметика

Нам знакома десятичная система исчисления, состоящая из одноразрядных чисел и многоразрядных. Цифра слева у многоразрядного числа в десять раз больше по значимости той, которая справа. Так, мы привыкли читать 2, 17, 467 и т. д. Совершенно другая логика и подход у раздела, который носит название «двоичная арифметика». Это и неудивительно, ведь двоичная арифметика создана не для человеческой логики, а для компьютерной. Если арифметика чисел произошла от счета предметов, что в дальнейшем абстрагировалось от свойств предмета к «голой» арифметике, то с компьютером такое не пройдет. Чтобы можно было поделиться своими знаниями с ЭВМ, человеку пришлось изобрести такую модель исчисления.

Двоичная арифметика работает с двоичным алфавитом, который состоит всего из 0 и 1. А использование этого алфавита называется двоичной системой исчисления.

Отличие двоичной арифметики от десятичной в том, что значимость позиции слева больше не в 10, а в 2 раза. Двоичные числа имеют вид 111, 1001 и т. д. Как понимать такие числа? Итак, рассмотрим число 1100:

1. Первая цифра слева — 1*8=8, помня о том, что четвертая цифра, а значит, ее нужно умножить на 2, получаем позицию 8.
2. Вторая цифра 1*4=4 (позиция 4).
3. Третья цифра 0*2=0 (позиция 2).
4. Четвертая цифра 0*1=0 (позиция 1).
5. Итак, наше число 1100=8+4+0+0=12.

То есть при переходе на новый разряд слева его значимость в двоичной системе умножается на 2, а в десятичной — на 10. Такая система имеет один минус: это слишком большой рост разрядов, которые необходимы для записи чисел. Примеры представления десятичных чисел в виде двочиных можно посмотреть в следующей таблице.

Десятичные числа в двоичном виде изображены ниже.

Используются также и восьмеричная, и шестнадцатеричная системы исчисления.

Эта загадочная арифметика

Что такое арифметика, «дважды два» или неизведанные тайны чисел? Как видим, арифметика, может, и кажется на первый взгляд простой, но ее неочевидная легкость обманчива. Ее можно изучать и детям вместе с тетушкой Совой из мультика «Арифметика-малышка», а можно погрузиться в глубоко научные изыскания чуть ли не философского порядка. В истории она прошла путь от счета предметов до поклонения красоте чисел. Одно только точно известно: с установлением основных постулатов арифметики вся наука может опираться на ее крепкое плечо.

Универсальная арифметика — это… Что такое Универсальная арифметика?

Латинское издание (1707) Английское издание (1720)

«Универсальная арифметика» (или «Всеобщая арифметика», лат. Arithmetica Universalis) — монография Исаака Ньютона, впервые опубликованная в 1707 году на латинском языке. Универсальной арифметикой Ньютон называл алгебру, и данный труд внёс существенный вклад в развитие этого раздела математики. Позднее книгу под таким же названием опубликовал Эйлер в 1768—1769 годах.

История создания

Среди курсов, которые вёл в Тринити-колледже Исаак Ньютон, был курс алгебры, и согласно правилам Ньютон сдал в университетскую библиотеку аккуратно оформленный латинский конспект этих лекций^[1]. После ухода Ньютона от преподавательской деятельности его преемник на кафедре, Уильям Уинстон опубликовал эту рукопись под названием «Универсальная арифметика». К первому изданию был приложен мемуар Галлея о численном методе нахождения корней уравнений. Книга вызвала большой интерес и неоднократно переиздавалась на разных языках; в XVIII веке вышли 5 только латинских её переизданий. Каждое новое издание сопровождалось растущим число комментариев и дополнений.

Краткое содержание

В начале книги Ньютон поясняет отношение арифметики и алгебры: цель алгебры — открыть и исследовать общие законы арифметики, а также предложить практические методы решения уравнений. Далее Ньютон даёт классическое определение вещественного числа как отношения результата измерения к единичному эталону^[2]:

Под числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой-нибудь величины к другой величине того же рода, принятой за единицу. Оригинальный текст  (лат.)   Per Numerum non tam multitudinem unitatum quam abstractam quantitatis cujusvis ad aliam ejusdem generis quantitattem quae pro unitate habetur rationem intelligimus.

Это определение фактически завершает многолетний процесс «уравнения в правах» целых, дробных и иррациональных чисел. В отличие от многих математиков того времени, Ньютон не рассматривал отдельно отрицательные числа и на примерах показал их полезность.

Затем излагается теория десятичных дробей, действий с ними и используемых обозначений. Ньютон в своих выкладках использовал обозначения Декарта, мало чем отличающиеся от современных. Однако, в отличие от Декарта, он полностью отделил алгебру от геометрии, подчеркнув, что при всей взаимной пользе у этих наук разные предметы.

В отдельных разделах, с многочисленными примерами и геометрическими иллюстрациями, излагаются действия с дробями, извлечение корней, типы уравнений, методы их упрощения и решения. Ньютон почти не приводит доказательств своих утверждений и основное внимание уделяет прикладным аспектам материала. Некоторые высказанные в книге глубокие теоремы удалось строго доказать только в XIX веке^[1].

Особое внимание Ньютон уделил решению алгебраических уравнений, эта тема занимает почти половину книги. В ходе изложения приводятся решения 77 типовых задач (в основном геометрического характера), снабжённые подробными разъяснениями и методическими рекомендациями.

Среди других открытий Ньютона, изложенных в книге, можно упомянуть:

Перевод на русский язык

Литература

• История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
• Никифоровский В. А. Из истории алгебры XVI-XVII вв. — М.: Наука, 1979. — С. 174-204. — 208 с. — (История науки и техники).
• Юшкевич А. П. О «Всеобщей арифметике» И. Ньютона. // В книге: Ньютон И. Всеобщая арифметика. М.: Изд. АН СССР, 1948, стр. 347-391.

Ссылки

Примечания