Значение слова арифметика википедия – Значение слова «Арифметика» в 10 онлайн словарях Даль, Ожегов, Ефремова и др.

арифметика — Викисловарь

Морфологические и синтаксические свойства[править]

падеж	ед. ч.	мн. ч.
Им.	арифме́тика	арифме́тики
Р.	арифме́тики	арифме́тик
Д.	арифме́тике	арифме́тикам
В.	арифме́тику	арифме́тики
Тв.	арифме́тикой арифме́тикою	арифме́тиками
Пр.	арифме́тике	арифме́тиках

а·риф-ме́-ти-ка (дореформ. ариѳметика)

Существительное, неодушевлённое, женский род, 1-е склонение (тип склонения 3a по классификации А. А. Зализняка).

Корень: -арифмет-; суффикс: -ик; окончание: -а ^{[Тихонов, 1996]}.

Произношение[править]

• МФА: ед. ч. [ɐrʲɪf⁽ʲ⁾ˈmʲetʲɪkə], мн. ч. [ɐrʲɪf⁽ʲ⁾ˈmʲetʲɪkʲɪ]

Семантические свойства[править]

Значение[править]

1. часть математики, изучающая простейшие свойства целых и дробных чисел и действия над ними ◆  — Помню, у нас в гимназии учителем арифметики был Сигизмунд Урбаныч, из поляков. А. П. Чехов, «Накануне поста», 1887 г.
2. перен., разг. то, что подсчитано, итог ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы[править]

1. —

Антонимы[править]

1. частичн.: высшая математика

Гиперонимы[править]

1. математика

Гипонимы[править]

1.  ?

Родственные слова[править]

Этимология[править]

Происходит от др.-греч. ἀριθμητική «искусство счёта, учение о числах, арифметика», далее из ἀριθμός «количество, число», далее из праиндоевр. *re(i)- «рассуждение, счёт».

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Библиография[править]

• Словарь новых слов русского языка (середина 50-х — середина 80-х годов) / Под ред. Н. З. Котеловой. — СПб. : Дмитрий Буланин, 1995. — ISBN 5-86007-016-0.

Морфологические и синтаксические свойства[править]

арифметика

Существительное.

Корень: —.

Произношение[править]

Семантические свойства[править]

Значение[править]

1. арифметика (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы[править]

1. —

Антонимы[править]

1. —

Гиперонимы[править]

1.  ?

Гипонимы[править]

1. —

Родственные слова[править]

Ближайшее родство

Этимология[править]

От ??

Фразеологизмы и устойчивые сочетания[править]

Библиография[править]

Морфологические и синтаксические свойства[править]

арифметика

Существительное.

Корень: —.

Произношение[править]

Семантические свойства[править]

Значение[править]

1. арифметика (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы[править]

1. —

Антонимы[править]

1. —

Гиперонимы[править]

1.  ?

Гипонимы[

Значение слова АРИФМЕТИКА. Что такое АРИФМЕТИКА?

Арифме́тика (др.-греч. ἀριθμητική; от ἀριθμός — число) — раздел математики, изучающий числа, их отношения и свойства. Предметом арифметики является понятие числа в развитии представлений о нём (натуральные, целые и рациональные, действительные, комплексные числа) и его свойствах. В арифметике рассматриваются измерения, вычислительные операции (сложение, вычитание, умножение, деление) и приёмы вычислений. Изучением свойств отдельных целых чисел занимается высшая арифметика, или теория чисел. Теоретическая арифметика уделяет внимание определению и анализу понятия числа, в то время как формальная арифметика оперирует логическими построениями предикатов и аксиом. Арифметика является древнейшей и одной из основных математических наук; она тесно связана с алгеброй, геометрией и теорией чисел.

Причиной возникновения арифметики стала практическая потребность в счёте, и вычислениях, связанных с задачами учёта при централизации сельского хозяйства. Наука развивалась вместе с усложнением задач, требующих решения. Большой вклад в развитие арифметики внесли греческие математики, в частности философы-пифагорейцы, пытавшиеся с помощью чисел постичь и описать все закономерности мира.

В Средние века арифметику относили, вслед за неоплатониками, к числу так называемых семи свободных искусств. Основными областями практического применения арифметики тогда были торговля, навигация, строительство. В связи с этим особое значение получили приближённые вычисления иррациональных чисел, необходимые в первую очередь для геометрических построений. Особенно бурно арифметика развивалась в Индии и странах ислама, откуда новейшие достижения математической мысли проникли в Западную Европу; Россия знакомилась с математическими знаниями «и от греков, и от латин».

С наступлением Нового времени мореходная астрономия, механика, усложнившиеся коммерческие расчёты поставили новые запросы к технике вычислений и дали толчок к дальнейшему развитию арифметики. В начале XVII века Непер изобрёл логарифмы, а затем Ферма выделил теорию чисел в самостоятельный раздел арифметики. К концу века сформировалось представление об иррациональном числе как о последовательности рациональных приближений, а в течение следующего столетия благодаря трудам Ламберта, Эйлера, Гаусса арифметика включила в себя операции с комплексными величинами, приобретя современный вид.

Последующая история арифметики ознаменована критическим пересмотром её основ, попытками дедуктивного её обоснования. Теоретические обоснования представления о числе связаны в первую очередь со строгим определением натурального числа и аксиомами Пеано, сформулированными в 1889 году. Непротиворечивость формального построения арифметики была показана Генценом в 1936 году.

Основам арифметики издавна и неизменно уделяется большое внимание в начальном школьном образовании.

Арифметика что это? Значение слова Арифметика

Значение слова Арифметика по Ефремовой:

Арифметика — 1. Раздел математики, изучающий простейшие свойства чисел, способы их записи и действия над ними.
2. Учебный предмет, содержащий основы данного раздела математики.
3. разг. Учебник, излагающий содержание данного учебного предмета.

Арифметика в Энциклопедическом словаре:

Арифметика — (от греч. arithmos число) — часть математики. изучаетпростейшие свойства чисел, в первую очередь натуральных (целыхположительных) и дробных, и действия над ними. Развитие арифметики привелок выделению из нее алгебры и чисел теории.

Значение слова Арифметика по словарю Ушакова:

АРИФМЕТИКА
арифметики, мн. нет, ж. (греч. arithmetike). Учение о числах, выражаемых цифрами, и действиях над ними.

Значение слова Арифметика по словарю Даля:

Арифметика
ж. греч. учение о счете, наука о счислении. основа всей математики (науки о величинах, о измеримом). стар. счетная или цифирная мудрость. счет, счисление, цифирная сметка, выкладка. Арифметичный, арифметический, к ней относящийся. Арифметик, в народе арифметчик м. сведущий в науке этой, счетчик, счислитель, выкладчик, цифирщик, сметчик. Общая

арифметика, алгебра, счисление буквами и другими знаками, со вставкою цифр в окончательный вывод. прикладная арифметика, именованные числа, приложение счета к делу, когда сочетаются не отвлеченные (безыменные) цифры, а деньги, мера, вес и пр.

Определение слова «Арифметика» по БСЭ:

Арифметика (греч. arithmetika, от arithmys — число)
наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними.
Владение достаточно развитым понятием натурального числа и умение производить действия с числами необходимы для практической и культурной деятельности человека. Поэтому А. является элементом дошкольного воспитания детей и обязательным предметом школьной программы.

С помощью натуральных чисел конструируются многие математические понятия (например, основное понятие математического анализа — действительное число). В связи с этим А. является одной из основных математических наук. Когда делается упор на логический анализ понятия числа, то иногда употребляют термин теоретическая арифметика. А. тесно связана с алгеброй, в которой, в частности, изучаются действия над числами без учёта их индивидуальных свойств. Индивидуальные свойства целых чисел составляют предмет чисел теории.
Историческая справка. Возникнув в глубокой древности из практических потребностей счёта и простейших измерений, А. развивалась в связи с усложнением хозяйственной деятельности и социальных отношений, денежными расчётами, задачами измерений расстояний, времени, площадей и требованиями, которые предъявляли к ней другие науки.
О возникновении счёта и о начальных стадиях образования арифметических понятий судят обычно по наблюдениям, относящимся к процессу счёта у первобытных народов, и, косвенным образом, путём изучения следов аналогичных стадий, сохранившихся в языках культурных народов и наблюдающихся при усвоении этих понятий детьми. Эти данные говорят о том, что развитие тех элементов мыслительной деятельности, которые лежат в основе процесса счёта, проходит ряд промежуточных этапов. К ним относятся: умение узнавать один и тот же предмет и различать предметы в подлежащей счёту совокупности предметов. умение устанавливать исчерпывающее разложение этой совокупности на элементы, отличимые друг от друга и вместе с тем равноправные при счёте (пользование именованной «единицей» счёта).
умение устанавливать соответствие между элементами двух множеств, вначале непосредственно, а затем сопоставлением их с элементами раз навсегда упорядоченной совокупности объектов, т. е. совокупности объектов, расположенных в определённой последовательности. Элементами такой стандартной упорядоченной совокупности становятся слова (числительные), применяемые при счёте предметов любой качественной природы и отвечающие образованию отвлечённого понятия числа. При самых различных условиях можно наблюдать сходные особенности постепенного возникновения и усовершенствования перечисленных навыков и отвечающих им арифметических понятий.
Сначала счёт оказывается возможным лишь для совокупностей из сравнительно небольшого числа предметов, за пределами которого количественные различия осознаются смутно и характеризуются словами, являющимися синонимами слова «много». при этом орудием счёта служат зарубки на дереве
(«бирочный» счёт), счётные камешки, чётки, пальцы рук и т.п., а также множества, заключающие постоянное число элементов, например: «глаза» — как синоним числительного «два», кисть руки («пясть») — как синоним и фактическая основа числительного
«пять», и т.п.
Словесный порядковый счёт (раз, два, три и т.д.), прямую зависимость которого от пальцевого счёта (последовательное произнесение названий пальцев, частей рук) в некоторых случаях можно проследить непосредственно, связывается в дальнейшем со счётом групп, содержащих определённое число предметов. Это число образует основание соответствующей системы счисления, обычно, в результате счёта по пальцам двух рук, равное 10. Встречаются, однако, и группировки по 5, по 20 (французское 80 «quatre-vingt» = 4 Ч 20),
по 40, по 12 («дюжина»), по 60 и даже по 11 (Новая Зеландия). В эпоху развитых торговых сношений способы нумерации (как устной, так и письменной) естественно обнаруживали тенденцию к единообразию у общавшихся между собой племён и народностей. это обстоятельство сыграло решающую роль в установлении и распространении применяемой в наст. время системы нумерации (счисления), принципа поместного (поразрядного) значения цифр и способов выполнения арифметических действий. По-видимому, аналогичными причинами объясняется и общеизвестное сходство имён числительных в различных языках: например, два — dva (санскр.), &delta.v&omicron. (греч.), duo (лат.), two (англ.).
Источником первых достоверных сведений о состоянии арифметических знаний в эпоху древних цивилизаций являются письменные документы Др. Египта (Папирусы математические), написанные приблизительно за 2 тыс. лет до н. э. Это — сборники задач с указанием их решений, правил действий над целыми числами и дробями со вспомогательными таблицами, без каких бы то ни было пояснений теоретического характера. Решение некоторых задач в этом сборнике производится, по существу, с помощью составления и решения уравнений. встречаются также арифметические и геометрические прогрессии.
О довольно высоком уровне арифметической культуры вавилонян за 2-3 тыс. лет до н. э. позволяют судить Клинописные математические тексты. Письменная нумерация вавилонян в клинописных текстах представляет собой своеобразное соединение десятичной системы (для чисел, меньших 60) с шестидесятиричной, с разрядными единицами 60, 60І и т.д. Наиболее существенным показателем высокого уровня А. является употребление шестидесятиричных дробей с распространением на них той же системы нумерации, аналогично современным десятичным дробям. Техника выполнения арифметических действий у вавилонян, в теоретическом отношении аналогичная обычным приёмам в десятичной системе, осложнялась необходимостью прибегать к обширным таблицам умножения (для чисел от 1 до 59). В сохранившихся клинописных материалах, представлявших собой, по-видимому, учебные пособия, находятся, кроме того, и соответствующие таблицы обратных чисел (двузначные и трёхзначные, т. е. с точностью до ¹/₆₀І и ¹/₆₀і), применявшихся при делении.
У древних греков практическая сторона А. не получила дальнейшего развития. применявшаяся ими система письменной нумерации с помощью букв алфавита была значительно менее приспособлена для производства сложных вычислений, нежели вавилонская (показательно, в частности, что древнегреческие астрономы предпочитали пользоваться шестидесятиричной системой). С другой стороны, древнегреческие математики положили начало теоретической разработке А. в части, касавшейся учения о натуральных числах, теории пропорций, измерения величин и — в неявной форме — также и теории иррациональных чисел.
В «Началах» Евклида (3 в. до н. э.) имеются сохранившие своё значение и до сих пор доказательство бесконечности числа простых чисел, основные теоремы о делимости, алгоритмы для нахождения общей меры двух отрезков и общего наибольшего делителя двух чисел (см. Евклида алгоритм), доказательство несуществования рационального числа, квадрат которого равен 2 (иррациональность числа &radic.2), и изложенная в геометрической форме теория пропорций. К рассматривавшимся теоретико-числовым задачам относятся задачи о совершенных числах (Евклид), о пифагоровых числах, а также — уже в более позднюю эпоху — алгоритм для выделения простых чисел (Эратосфена решето) и решение ряда неопределённых уравнений 2-й и более высоких степеней (Диофант).
Существенную роль в образовании понятия бесконечного натурального ряда чисел сыграл «Псаммит» Архимеда (3 в. до н. э.), в котором доказывается возможность именовать и обозначать сколь угодно большие числа. Сочинения Архимеда свидетельствуют о довольно высоком искусстве в получении приближённых значений искомых величин: извлечение корня из многозначных чисел, нахождение рациональных приближений для иррациональных чисел, например

&radic.Ї3 &asymp.

265 153

.   3

10 71

1  7

.

Римляне не продвинули вперёд технику вычислений, оставив, однако, дошедшую до нашего времени систему нумерации (римские цифры), мало приспособленную для производства действий и применяемую в настоящее время почти исключительно для обозначения порядковых чисел.
Трудно проследить преемственность в развитии математики в отношении предыдущих, более древних, культур. однако чрезвычайно важные этапы в развитии А. связываются с культурой Индии, оказавшей влияние как на страны Передней Азии и Европы, так и на страны Вост. Азии (Китай, Япония). Помимо применения алгебры к решению задач арифметического содержания, наиболее существенная заслуга индийцев — введение позиционной системы счисления (с применением десяти цифр, включая нуль для обозначения отсутствия единиц в каком-либо из разрядов), сделавшей возможной разработку сравнительно простых правил выполнения основных арифметических действий.
Учёные средневекового Востока не только сохранили в переводах наследие древнегреческих математиков, но и содействовали распространению и дальнейшему развитию достижений индийцев. Методы выполнения арифметических действий, в значительной части ещё далёкие от современных, но уже использующие преимущества позиционной системы счисления, с 10 в. н. э. стали постепенно проникать в Европу, раньше всего в Италию и Испанию.
Сравнительно медленный прогресс А. в средние века сменяется к началу 17 в. быстрым усовершенствованием приёмов вычисления в связи с возросшими практическими запросами к технике вычислений (задачи мореходной астрономии, механики, усложнившиеся коммерческие расчёты и т.п.). Дроби со знаменателем 10, употреблявшиеся ещё индийцами (при извлечении квадратных корней) и неоднократно обращавшие на себя внимание и европейских учёных, применялись сначала в неявной форме в тригонометрических таблицах (в форме целых чисел, выражающих длины линий синуса, тангенса и т.д. при радиусе, принятом за 10⁵). Впервые (1427) подробно описал систему десятичных дробей и правила действий над ними аль-Каши. Запись десятичных дробей, по существу совпадающая с современной, встречается в сочинениях С. Стевина в 1585 и с этого времени получает повсеместное распространение. К той же эпохе относится изобретение логарифмов в начале 17 в. Дж. Непером. В начале 18 в. приёмы выполнения и записи вычислений приобретают современную форму.
В России до начала 17 в. применялась нумерация, сходная с греческой. хорошо и своеобразно была разработана система устной нумерации, доходившая до 50-го разряда. Из русских арифметических руководств начала 18 в. наибольшее значение имела высоко оцененная М. В. Ломоносовым
«Арифметика» Л. Ф. Магницкого (1703). В ней содержится следующее определение А.: «Арифметика или числительница, есть художество честное, независтное, и всем удобопонятное, многополезнейшее, и многохвальнейшее, от древнейших же и новейших, в разные времена живших изряднейших арифметиков, изобретенное, и изложенное».
Наряду с вопросами нумерации, изложением техники вычисления с целыми числами и дробями (в т. ч. и десятичными) и соответствующими задачами в этом руководстве содержатся и элементы алгебры, геометрии и тригонометрии, а также ряд практических сведений, относящихся к коммерческим расчётам и задачам навигации. Изложение А. приобретает уже более или менее современный вид у Л. Эйлера и его учеников.
Теоретические вопросы арифметики. Теоретическая разработка вопросов, касающихся учения о числе и учения об измерении величин, не может быть оторвана от развития математики в целом: решающие этапы её связаны с моментами, определявшими в равной мере и развитие алгебры, геометрии и анализа. Наиболее важным надо считать создание общего учения о Величинах, соответствующего абстрактного учения о числе (целом, рациональном и иррациональном) и буквенного аппарата алгебры.
Фундаментальное значение А. как науки, достаточной для изучения непрерывных величин различного рода, было осознано лишь к концу 17 в. в связи со включением в А. понятия иррационального числа, определяемого последовательностью рациональных приближений. Немаловажную роль при этом сыграли аппарат десятичных дробей и применение логарифмов, расширивших область осуществляемых с требуемой точностью операций над действительными числами (иррациональными наравне с рациональными).
И. Ньютон, впервые высказавший общее определение числа как отношения двух значений какой-либо величины, всё ещё избегал, однако, записывать найденные им законы в виде формул, выражающих значение одной из величин через значения других, неоднородных с ней, и предпочитал придавать такого рода соотношениям форму пропорций. Например, y₁/y₂ = x₁І/x₂І вместо соответствующей формулы y = kxІ.
Современная точка зрения, согласно которой все буквы в формулах означают просто числа и действия производятся над числами, равноправными между собой, независимо от их конкретного происхождения, ещё и сейчас в элементарном преподавании иногда осознаётся не в достаточной степени (это сказывается в наименованиях при записи действий, в избыточной осторожности при определении производных физ. величин и т.п.).
Аксиоматическое построение арифметики. Начало следующего этапа — аксиоматических построение А. — относится уже к 19 в. и связано с общим процессом критического пересмотра логических основ математики, в котором важнейшую роль сыграли, в частности, работы Н. И. Лобачевского по геометрии. Самая простота и очевидная бесспорность начальных положений А. затрудняли выделение основных положений — аксиом и определений, которые могли бы служить исходным пунктом построения теории. Первые намёки на возможность такого построения имеются уже в доказательстве соотношения 2
Ч 2= 4, данном Г. Лейбницем (см. ниже).
Лишь в сер. 19 в. Г. Грасману удалось выбрать систему основных аксиом, определяющих действия сложения и умножения так, чтобы остальные положения А. вытекали из неё как логическое следствие. Если иметь в виду натуральный ряд чисел, начиная от 1, и определить 2 как 1+1, 3 как 2+1, 4 как 3+1 и т.д., то одного общего положения а +(b + 1) = (а + b)+ 1, принимаемого в качестве аксиомы или определения сложения, оказывается достаточно для того, чтобы не только вывести формулы частного типа, как, например, 3+2 = 5, но, пользуясь методом математической индукции, доказать и общие свойства сложения, верные для любых натуральных чисел, — переместительный и сочетательный законы. Подобную же роль для умножения играют формулы а·1 = а и а (b + 1) = ab + а.
Так, упомянутое выше доказательство соотношения 2·2 = 4 можно представить в виде цепочки равенств, вытекающей из приведённых здесь формул и определения чисел 2, 3 и 4, именно: 2·2 = 2(1 + 1) = 2·1 + 2·1 = 2 + 2 = 2 + (1 + 1) = (2 + 1) + 1 = 3 + 1 = 4.
После доказательства переместительного (см. Коммутативность), сочетательного (см. Ассоциативность) и распределительного (см. Дистрибутивность) (по отношению к сложению) законов действия умножения дальнейшее построение теории арифметических действий над натуральными числами не представляет уже принципиальных затруднений. Если оставаться на том же уровне абстракции, то дробные числа приходится вводить как пары целых чисел (числитель и знаменатель), подчинённые определённым законам сравнения и действий (см. Дробь).
Построение Грасмана было завершено в дальнейшем работами Дж. Пеано, в которых отчётливо выделена система основных (не определяемых через другие понятия) понятий, именно: понятие натурального числа, понятие следования одного числа непосредственно за другим в натуральном ряде и понятие начального члена натурального ряда (за который можно принять 0 или 1). Эти понятия связаны между собой пятью аксиомами, которые можно рассматривать как аксиоматическое определение указанных основных понятий.
Аксиомы Пеано: 1) 1 есть натуральное число. 2) следующее за натуральным числом есть натуральное число. 3) 1 не следует ни за каким натуральным числом. 4) если натуральное число а следует за натуральным числом b и за натуральным числом c, то b и c тождественны. 5) если какое-либо предложение доказано для 1 и если из допущения, что оно верно для натурального числа n, вытекает, что оно верно для следующего за п натурального числа, то это предложение верно для всех натуральных чисел. Эта аксиома — аксиома полной индукции — даёт возможность в дальнейшем пользоваться грасмановскими определениями действий и доказывать общие свойства натуральных чисел.
Эти построения, дающие решение задачи обоснования формальных положений А., оставляют в стороне вопрос о логической структуре А. натуральных чисел в более широком смысле слова, с включением тех операций, которые определяют собой приложения А. как в рамках самой математики, так и в практической жизни. Анализ этой стороны вопроса, выяснив содержание понятия количественного числа, вместе с тем показал, что вопрос об обосновании А. тесно связан с более общими принципиальными проблемами методологического анализа математических дисциплин. Если простейшие предложения А., относящиеся к элементарному счёту объектов и являющиеся обобщением многовекового опыта человечества, естественно укладываются в простейшие логические схемы, то А. как математическая дисциплина, изучающая бесконечную совокупность натуральных чисел, требует исследования непротиворечивости соответствующей системы аксиом и более детального анализа смысла вытекающих из неё общих предложений.
Лит.: Клейн Ф., Элементарная математика с точки зрения высшей, пер. с нем. т. 3 изд., т. 1, М.-Л., 1935. Арнольд И. В., Теоретическая арифметика, 2 изд., М., 1939. Беллюстин В. К., Как постепенно дошли люди до настоящей арифметики, М., 1940. Гребенча М. К., Арифметика, 2 изд., М., 1952. Берман Г. Н., Число и наука о ней, 3 изд., М., 1960. Дептяан И. Я., История арифметики, 2 изд., М., 1965. Выгодский М. Я., Арифметика и алгебра в Древнем мире, 2 изд., М., 1967.
И. В. Арнольд.

---

Длинная арифметика — Википедия

Длинная арифметика — выполняемые с помощью вычислительной машины арифметические операции (сложение, вычитание, умножение, деление, возведение в степень, элементарные функции) над числами, разрядность которых превышает длину машинного слова данной вычислительной машины. Эти операции реализуются не аппаратно, а программно, с использованием базовых аппаратных средств работы с числами меньших порядков. Частный случай — арифметика произвольной точности — относится к арифметике, в которой длина чисел ограничена только объёмом доступной памяти.

Длинная арифметика применяется в следующих областях:

Необходимые аппаратные средства для работы с длинной арифметикой[править | править код]

Строго говоря, для реализации арифметики произвольной точности от процессора требуется лишь косвенная адресация; в арифметике фиксированной точности можно обойтись даже без неё. Тем не менее, определённые функции процессора ускоряют длинную арифметику, одновременно упрощая её программирование.

Реализация в языках программирования[править | править код]

Языки программирования имеют встроенные типы данных, размер которых, в основном, не превышает 64 бита (около 10¹⁹). Десятичная длинная арифметика была реализована в советских языках программирования АЛМИР-65 на ЭВМ МИР-1 и АНАЛИТИК на ЭВМ МИР-2. Для работы с большими числами, в современных языках программирования существует довольно много готовых оптимизированных библиотек для длинной арифметики.

Большинство функциональных языков позволяют переключаться с обычной арифметики на длинную без необходимости изменения кода арифметических расчётов. Например, Erlang и Scheme всегда представляют точные числа длинными. В Standard ML реализации всех разновидностей целых чисел определяются на основании сигнатуры INTEGER, позволяя выбирать необходимую размерность,— в том числе присутствует модуль IntInf, реализующий целые числа произвольной точности; в реализации PolyML этот модуль используется по умолчанию.

Встроенные библиотеки работы с большими числами есть в Ruby, Python и Java.

Алгоритмы умножения[править | править код]

Для описания алгоритмов обычно используется следующее представление целых чисел. Выбирается основание β>1{\displaystyle \beta >1}. Тогда целое число длины n{\displaystyle n} можно представить в виде^[1]:

A=an−1⋅βn−1+…+a1⋅β+a0,{\displaystyle A=a_{n-1}\cdot \beta ^{n-1}+…+a_{1}\cdot \beta +a_{0},}

где 0≤ai≤β−1.{\displaystyle 0\leq a_{i}\leq \beta -1.}

Базовый[править | править код]

Представляет собой алгоритм по школьному методу «в столбик». Занимает время O(n⋅m),{\displaystyle O(n\cdot m),} где n,m{\displaystyle n,m} — размеры перемножаемых чисел.

Алгоритм может быть представлен в виде^[1][2]:

Algorithm 1 BasecaseMultiply
Input: A=∑i=0m−1aiβi,B=∑j=0n−1bjβj{\displaystyle A=\sum \nolimits _{i=0}^{m-1}a_{i}\beta ^{i},B=\sum \nolimits _{j=0}^{n-1}b_{j}\beta ^{j}}
Output: C=AB:=∑k=0m+n−1ckβk{\displaystyle C=AB:=\sum \nolimits _{k=0}^{m+n-1}c_{k}\beta ^{k}}
1:C←A⋅b0{\displaystyle 1:C\gets A\cdot b_{0}}
2:{\displaystyle 2:} for j{\displaystyle j} from 1{\displaystyle 1} to n−1{\displaystyle n-1} do
3:    C←C+βj(A⋅bj){\displaystyle 3:~~~~C\gets C+\beta ^{j}(A\cdot b_{j})}
4:return  C.{\displaystyle 4:return~~C.}

Умножение Карацубы[править | править код]

Метод умножения Карацубы относится к парадигме «разделяй и властвуй». Сложность вычисления алгоритма:

M(n)=O(nlog2⁡3),log2⁡3=1,5849…{\displaystyle M(n)=O(n^{\log _{2}3}),\quad \log _{2}3=1{,}5849\ldots }.

Данный алгоритм представляет собой простую реализацию^[3] идеи разделения входных данных, которая стала базисной для нижеперечисленных алгоритмов. Идея заключается в разделении одной операции умножения над n{\displaystyle n}-значными числами на три операции умножения над числами длины n/2{\displaystyle n/2} плюс O(n){\displaystyle O(n)}^[1].

Для перемножения двух чисел, превышающих длину машинного слова, алгоритм Карацубы вызывается рекурсивно до тех пор, пока эти числа не станут достаточно маленькими, чтобы их можно было перемножить непосредственно. Пример такого алгоритма:

Algorithm 2 KaratsubaMultiply
Input: A=∑i=0n−1aiβi,B=∑j=0n−1bjβj{\displaystyle A=\sum \nolimits _{i=0}^{n-1}a_{i}\beta ^{i},B=\sum \nolimits _{j=0}^{n-1}b_{j}\beta ^{j}}
Output: C=AB:=∑k=02n−1ckβk{\displaystyle C=AB:=\sum \nolimits _{k=0}^{2n-1}c_{k}\beta ^{k}}
k←[n/2]{\displaystyle k\gets [n/2]}
(A0,B0):=(A,B)modβk,(A1,B1):=(A,B)divβk{\displaystyle (A_{0},B_{0}):=(A,B)mod\beta ^{k},(A_{1},B_{1}):=(A,B)div\beta ^{k}}
sA←sign(A0−A1),sB←sign(B0−B1){\displaystyle s_{A}\gets sign(A_{0}-A_{1}),s_{B}\gets sign(B_{0}-B_{1})}
C0←{\displaystyle C_{0}\gets } KaratsubaMultiply(A0,B0){\displaystyle (A_{0},B_{0})}
C1←{\displaystyle C_{1}\gets } KaratsubaMultiply(A1,B1){\displaystyle (A_{1},B_{1})}
C2←{\displaystyle C_{2}\gets } KaratsubaMultiply(|A0−A1|,|B0−B1|){\displaystyle (|A_{0}-A_{1}|,|B_{0}-B_{1}|)}
return C:=C0+(C0+C1−sAsBC2)βk+C1β2k{\displaystyle return~C:=C_{0}+(C_{0}+C_{1}-s_{A}s_{B}C_{2})\beta ^{k}+C_{1}\beta ^{2k}}

Посчитаем x=12345⋅6789{\displaystyle x=12345\cdot 6789}:

12345=12⋅1000+345{\displaystyle 12345=12\cdot 1000+345}

6789=6⋅1000+789{\displaystyle 6789=6\cdot 1000+789}

Нужно вычислить три промежуточных коэффициента:

C0=345⋅789=272205{\displaystyle C_{0}=345\cdot 789=272205}

C1=12⋅6=72{\displaystyle C_{1}=12\cdot 6=72}

C2=C1+C0−(345−12)⋅(789−6)=72+272205−333⋅783=11538{\displaystyle C_{2}=C_{1}+C_{0}-(345-12)\cdot (789-6)=72+272205-333\cdot 783=11538}

Результат:

x=C1⋅10002+C2⋅1000+C0{\displaystyle x=C_{1}\cdot 1000^{2}+C_{2}\cdot 1000+C_{0}}

x=72⋅10002+11538⋅1000+272205=83810205{\displaystyle x=72\cdot 1000^{2}+11538\cdot 1000+272205=83810205}

Алгоритм Тоома[править | править код]

Этот алгоритм является обобщением алгоритма Карацубы и работает быстрее. Для двух данных целых чисел A{\displaystyle A} и B{\displaystyle B} алгоритм Toom-a делит их на k{\displaystyle k} меньших частей, длина каждой из которых равна длине машинного слова, и производит операции над этими частями. Сложность вычисления алгоритма: O(nln⁡(2k−1)/ln⁡(k)).{\displaystyle O(n^{\ln(2k-1)/\ln(k)}).}

Алгоритм Тоома-3[править | править код]

Идея впервые была предложена А. Л. Тоомом в 1963 году^[4], и заключается в разделении входных данных (множителей) на 3 равные части (для простоты все части считаем равными). Toom-3 сокращает число элементарных операций умножения с 9 до 5. Сложность алгоритма O(n1.465).{\displaystyle O(n^{1.465}).}

Рассмотрим данный алгоритм на следующем примере. Пусть дано два числа Y{\displaystyle Y} и X{\displaystyle X}. Пусть определены операции над числами, размер которых равен 1/3 от размеров исходных чисел (см. рисунок). Предположим также, что числа занимают равную память и делятся ровно на 3 части, в противном случае дополним оба числа нулями до необходимых размеров.

Затем происходит отображение (параметризация) этих частей на полиномы 2 степени.

X(t)=x2⋅t2+x1⋅t+x0,{\displaystyle X(t)=x_{2}\cdot t^{2}+x_{1}\cdot t+x_{0},}

Y(t)=y2⋅t2+y1⋅t+y0,{\displaystyle Y(t)=y_{2}\cdot t^{2}+y_{1}\cdot t+y_{0},}

Введем b{\displaystyle b}, по определению такую, что значения многочленов X(b), Y(b){\displaystyle X(b),~Y(b)} соответственно равны входным числам x{\displaystyle x} и y{\displaystyle y}. Для битового представления чисел это число равно двойке в степени, равной длине каждой из частей в битах.

Также введем полином:

W(t)=X(t)⋅Y(t),{\displaystyle W(t)=X(t)\cdot Y(t),} (1)

W(t)=w4⋅t4+w3⋅t3+w2⋅t2+w1⋅t+w0,{\displaystyle W(t)=w_{4}\cdot t^{4}+w_{3}\cdot t^{3}+w_{2}\cdot t^{2}+w_{1}\cdot t+w_{0},}

После того как будут определены элементы wi{\displaystyle w_{i}} — коэффициенты многочленаW(t){\displaystyle W(t)}, они будут использованы в целях получения w=W(b){\displaystyle w=W(b)}, так как x⋅y=X(b)⋅Y(b)=W(b){\displaystyle x\cdot y=X(b)\cdot Y(b)=W(b)}. Размер коэффициентов wi{\displaystyle w_{i}} в 2 раза больше (по памяти), чем разбиение xi{\displaystyle x_{i}} или yi{\displaystyle y_{i}}. Конечное число, равное произведению x⋅y{\displaystyle x\cdot y} можно найти, складывая wi{\displaystyle w_{i}} со сдвигом, как показано на рисунке ниже.

Коэффициенты wi{\displaystyle w_{i}} могут быть вычислены следующим образом: w4=x2⋅y2,w3=x2⋅y1+x1⋅y2,  w2=x2⋅y0+x1⋅y1+x0⋅y2{\displaystyle w_{4}=x_{2}\cdot y_{2},w_{3}=x_{2}\cdot y_{1}+x_{1}\cdot y_{2},~~w_{2}=x_{2}\cdot y_{0}+x_{1}\cdot y_{1}+x_{0}\cdot y_{2}} и так далее, но это потребует все 9 перемножений: xi⋅yj{\displaystyle x_{i}\cdot y_{j}} для i, j=0,1,2, и будет эквивалентно простому перемножению.

Вместо этого был использован иной подход. X(t),Y(t){\displaystyle X(t),Y(t)} вычисляются в (1) в 5 точках при разных t{\displaystyle t}.

В таблице, представленной ниже, приведены значения полиномов в равенстве (1)

Параметр t=∞{\displaystyle t=\infty } условный. Он означает банальное равенство коэффициентов при t4{\displaystyle t^{4}}, тем самым мы получим значение w4{\displaystyle w_{4}} сразу. Данная система линейна относительно 5 неизвестных. При её разрешении мы получаем неизвестные wi{\displaystyle w_{i}}. Далее получаем значение многочлена, как было описано выше.

Алгоритм Тоома-4[править | править код]

Сложность алгоритма O(n1.404).{\displaystyle O(n^{1.404}).} Представляет собой 7 элементарных операций умножения. Toom-4 разделяет входные данные на 4 части.

По такому же принципу как и в Toom-3 строим два полинома:

X(t)=x3⋅t3+x2⋅t2+x1⋅t+x0,{\displaystyle X(t)=x3\cdot t^{3}+x2\cdot t^{2}+x1\cdot t+x0,}

Y(t)=y3⋅t3+y2⋅t2+y1⋅t+y0.{\displaystyle Y(t)=y3\cdot t^{3}+y2\cdot t^{2}+y1\cdot t+y0.}

X(t){\displaystyle X(t)}

Арифметика Википедия

Арифме́тика (др.-греч. ἀριθμητική, arithmētikḗ — от ἀριθμός, arithmṓs «число») — раздел математики, изучающий числа, их отношения и свойства. Предметом арифметики является понятие числа (натуральные, целые, рациональные, вещественные, комплексные числа) и его свойства. В арифметике рассматриваются измерения, вычислительные операции (сложение, вычитание, умножение, деление) и приёмы вычислений. Изучением свойств отдельных целых чисел занимается высшая арифметика, или теория чисел. Теоретическая арифметика уделяет внимание определению и анализу понятия числа, в то время как формальная арифметика оперирует логическими построениями предикатов и аксиом. Арифметика является древнейшей и одной из основных математических наук; она тесно связана с алгеброй, геометрией и теорией чисел^[1][2].

Причиной возникновения арифметики стала практическая потребность в счёте и вычислениях, связанных с задачами учёта при централизации сельского хозяйства. Наука развивалась вместе с усложнением задач, требующих решения. Большой вклад в развитие арифметики внесли греческие математики — в частности, философы-пифагорейцы, пытавшиеся с помощью чисел постичь и описать все закономерности мира.

В Средние века арифметику относили, вслед за неоплатониками, к числу так называемых семи свободных искусств. Основными областями практического применения арифметики тогда были торговля, навигация, строительство. В связи с этим особое значение получили приближённые вычисления иррациональных чисел, необходимые, в первую очередь, для геометрических построений. Особенно бурно арифметика развивалась в Индии и странах ислама, откуда новейшие достижения математической мысли проникли в Западную Европу; Россия знакомилась с математическими знаниями «и от греков, и от латин».

С наступлением Нового времени мореходная астрономия, механика, усложнившиеся коммерческие расчёты выдвинули новые требования к технике вычислений и дали толчок к дальнейшему развитию арифметики. В начале XVII века Непер изобрёл логарифмы, а затем Ферма выделил теорию чисел в самостоятельный раздел арифметики. К концу века сформировалось представление об иррациональном числе как о последовательности рациональных приближений, а в течение следующего столетия благодаря трудам Ламберта,

Интервальная арифметика — Википедия

Материал из Википедии — свободной энциклопедии

Интервальная арифметика — математическая структура, которая для вещественных интервалов определяет операции, аналогичные обычным арифметическим. Эту область математики называют также интервальным анализом или интервальными вычислениями. Данная математическая модель удобна для исследования различных прикладных объектов:

• Величины, значения которых известны только приближённо, то есть определён конечный интервал, в котором эти значения содержатся.
• Величины, значения которых в ходе вычислений искажены ошибками округления.
• Случайные величины.

Объекты и операции интервальной арифметики можно рассматривать как обобщение модели вещественных чисел, поэтому интервалы в ряде источников называются интервальными числами. Практическая важность этой модели связана с тем, что результаты измерений и вычислений почти всегда имеют некоторую погрешность, которую необходимо учесть и оценить.

Мы будем рассматривать всевозможные конечные вещественные интервалы [a,b] (a⩽b){\displaystyle [a,b]\ (a\leqslant b)}. Операции над ними определяются следующим образом:

• Сложение: [a,b] + [c,d] = [a + c, b + d]
• Вычитание: [a,b] − [c,d] = [a − d, b − c]
• Умножение: [a,b] × [c,d] = [min (ac, ad, bc, bd), max (ac, ad, bc, bd)]
• Деление: [a,b] / [c,d] = [min (a/c, a/d, b/c, b/d), max (a/c, a/d, b/c, b/d)]

Из определения видно, что интервал-сумма содержит всевозможные суммы чисел из интервалов-слагаемых и определяет границы множества таких сумм. Аналогично трактуются прочие действия. Отметим, что операция деления определена только в том случае, когда интервал-делитель не содержит нуля.

Вырожденные интервалы, у которых начало и конец совпадают, можно отождествить с обычными вещественными числами. Для них данные выше определения совпадают с классическими арифметическими действиями.

Сложение и умножение интервалов коммутативны и ассоциативны. Дистрибутивное свойство имеет место в ослабленном виде:

X(Y+Z)⊂XY+XZ{\displaystyle X(Y+Z)\subset XY+XZ}

Варианты и расширения интервальной арифметики[править | править код]

Стандарт компьютерной реализации интервальной арифметики IEEE 1788-2015 был принят в июне 2015 года.^[1] Рабочей группой по подготовке стандарта были подготовлены две свободно распространяемые референсные его реализации:^[2] библиотека C++ libieeep1788^[3] library for C++, и пакет, реализующий интервальные вычисления для свободного математического ПО GNU Octave^[4].

Минимальное подмножество стандарта, предназначенное для упрощения и ускорения его реализации — IEEE Std 1788.1-2017, было принято в декабре 2017 и опубликовано в феврале 2018.^[5]

Существует много реализаций интервальной арифметики в различных пакетах программного обеспечения^[6]. Зачастую они оформляются как специализированные библиотеки. Ряд компиляторов Fortran и C++ включают в себя поддержку интервальных значений как специального типа данных.

Обсуждение:Арифметика — Википедия

Материал из Википедии — свободной энциклопедии

Рецензия на 26 октября 2012 года[править код]

Дело близится к концу, хотелось бы услышать комментарии. Zanka 02:01, 26 октября 2012 (UTC)

В преамбуле можно дать ссылки на разделы, где будет говориться о теме подробнее. В разделе «Предмет арифметики» я ожидал увидеть, рассуждения для чего нужна арифметика и чем занимается, но никак не психологию первобытных народов. Было бы проще читать если упомянуть предмет арифметики в начале параграфа и позже порассуждать о происхождении арифметики в историческом плане. Кроме того не отражено как комплексные числа помогают счёту — в этом параграфе вообще мало о предмете арифметики. Зачем нужно сравнение множеств в этой части? Это тоже предмет арифметики? А почему операции над множествами не рассмотрены? В целом статья смотрится неоднородно из-за наличия истории, и отсутствия арифметики. Относятся ли к арифметики операции с числами в памяти компьютера? Alexander Mayorov 17:17, 26 октября 2012 (UTC)

Спасибо за мнение. Постараюсь ответить по порядку. Ссылки из преамбулы, такое новшество в статьях, которое мне не нравится, поэтому пока добавлять не собираюсь. Раздел «Предмет арифметики» до вчерашнего дня назывался «Элементарная арифметика», но оказалось, что для арифметики «элементарная» означает «формальная», а формальная арифметика — это уже мат.логика. Возможно имело смысл по-другому назвать раздел, но идея была вот в чём: арифметика — это собственно счёт, числа, операции, законы. Причём арифметика — это не столько все эти элементы, сколько история их развития. Всё это хорошо видно в книгах и энциклопедических статьях. Не совсем понятно про комплексные числа: они просто появились в какой-то момент и с ними тоже надо было определить арифметические операции. Сравнение множеств в самом первом абзаце самого первого раздела — это просто начало, что было когда не было числа и как появилось число. Если убрать минимальную историю из первого раздела, то там окажется то же, что уже есть во введении. По поводу арифметических операций в памяти компьютера: я планирую расширить раздел про арифмометры, они упоминаются во многих статьях связанных с арифметикой и тогда, видимо допишу и про компьютеры. К сожалению фундаментальных современных трудов нет, а в статьях я встречала понятие — арифметика больших чисел, относящееся в первую очередь к особенностям выполнения операций на компьютере. Zanka 20:35, 26 октября 2012 (UTC)

Тогда приведите источники во введении. По предмету не всё. Не может получиться бесконечный ряд при счёте предметов, поэтому для счёта бесконечные числа не нужны. Почему про технические аспекты ничего не сказано? Как собственно складывать числа? Деление с остатком не рассмотрено, а ведь оно важно для счёта. Деление столбиком.Alexander Mayorov 21:05, 26 октября 2012 (UTC)

Вы так вольно ходите по тексту, что я потерялась, извините. Давайте я разобью по пунткам. Мне думается будет удобнее, если вы сможете отвечать также в разных ветках. Извините, я работаю медленно. Zanka 14:02, 27 октября 2012 (UTC)

• Введение. Уточнить, что к арифметике как таковой относится и история развития понятия числа и операций. Проставить ссылки на источники. Сделано Посмотрите, я поправила первый абзац введения, так лучше? Исторический абзац и культурные влияния снабжены источниками в соответствующих разделах. Zanka 14:02, 27 октября 2012 (UTC)
• Предмет арифметики. 1. В самом начале добавить обобшающие предложения. 2. Убрать большое количество истории. 3. Добавить техническую информацию по операциям и 4. деление с остатком. Попробую кое-что убрать и переставить акценты с первобытных людей на детей, так как этот момент мне кажется важным именно в этой части статьи. Как осуществлять операции частично уже есть, на простейшем уровне (пересчёт для сложения, и т.п.), ещё добавлю. Zanka 14:02, 27 октября 2012 (UTC)
• Давайте по-порядку. Основная проблема в том, что статья сильно неоднородна, поскольку в ней идёт речь об истории, и частью о фомальных вещах. Поэтому это смотрится как несвязанные между собой вещи.
• В преамбуле должно быть по логике кракое описание статьи, то есть эта часть имеет смысл аннотации, и её можно написать в самом конце.
• Так что если не будет чёткого определения задач и предмета арифметики не будет видна логика. Я её и не вижу — почему исторический очерк в конце, а психология в самом начале?
• Предложение такое: дать определение арифметики, написать о предмете арифметики, и после расписать последовательно о конкретных вещах более подробнее. Если рассматриваются числа, то в истории должно быть зачем они нужны, а то я не понимаю зачем нужны комплексные числа для счёта яблок. Определение должно быть хотя бы близким к нормальному [1]. Alexander Mayorov 17:33, 27 октября 2012 (UTC)

По-порядку так по-порядку :). Временно забыли про введение. Предмет арифметики (ссылки текстом, никакой викификации, просто как заготовка):

Предметом арифметики является понятие числа как конкретной, вполне определённой, величины и его свойства, действия с числами(эсбе). В основном арифметика занимается изучением натуральных и рациональных чисел, или дробей(бсэ). На основе аксиоматической структуры множества натуральных чисел осуществляется построение других чиловых множеств, включая целые, действительные и комплексные числа, проводится их анализ(мэ). К основным действиям над числами относят в первую очередь сложение, вычитание, умножение и деление(эсбе), реже возведение в степень, извлечение корней(брит) и решение численных уравнений (эсбе). Исторически список арифметических действий также включал собственно счёт, удвоение, деление на два и деление с остатком как отдельные действия независимые от собственно умножения и деления, нахождение суммы арифметической и геометрической прогрессий (источники есть). Деление арифметических действий от Непера (см. в статье). В целом, осуществление и исследование операций над различными объектами называют арифметикой, как-то «арифметика квадратичных форм», «арифметика матриц»(мэ). К арифметике также относят исторические вопросы, связанные с происхождением и развитием понятия числа(мэ), и измерения(брит).

Математические расчёты и измерения, необходимые для практических нужд, как то пропорции, проценты, тройное правило, относят к низшей или практической арифметике(эсбе), в то время как логический анализ понятия числа относят к теоретической арифметике(мэ). Свойства целых чисел, деление их на части, построение непрерывных дробей являются составной частью теории чисел (мэ), которая долгое время носила название высшей арифметики (эсбе). Арифметика также тесно связана с алгеброй, которая занимается изучением собственно операций без учёта особенностей и свойств чисел (мэ, бсэ). Такие арифметические действия как возведение в степень, извлечение корней и решение численных уравнений являются технической частью алгебры. В этом ключе, вслед за Ньютоном и Гауссом, алгебру принято считать обобщением арифметики(эсбе, брит).

Арифметика как математическая дисциплина занимается изучением «бесконечной совокупности натуральных чисел». Как и прочие дисциплины она сталкивается с принципиальными методологическими проблемами, для неё необходимо исследование вопросов непротиворечивости и полноты аксиом (бсэ). Логическими построениями формальной системы предикатов и аксиом арифметики занимается формальная арифметика (бсэ_фа).

Это то что вы хотели? Zanka 20:36, 29 октября 2012 (UTC)

Если есть возможность, посмотрите по ссылкам энциклопедические статьи (помимо бсэ, который вы мне выше дали): Математическая энциклопедия, ЭСБЕ/Арифметика, наука, Britannica. Обратите внимание, у нас обычно идёт сразу за определением исторический очерк, а потом аксиомы Пеано и что-то про теоретические обоснования и формализацию. В британнике материал даётся с меньшим количеством истории. Так же и у нас в энциклопедии элементарной математики, откуда я брала определения. Я считаю, что большая часть истории должна быть отдельным разделом. Встаёт вопрос куда его поместить? Либо пусть он остаётся там где есть, либо переносить наверх после предмета арифметики, но в таком случае это будет означать разрыв повествования про собственно арифметику. … Хотя я опять убежала, это потом, пока предмет арифметики. Zanka 20:36, 29 октября 2012 (UTC)

Здесь у меня нет претензий. А что касается истории, я бы отказался от дублирования информации в этой статье и в истории арифметики. История и так везде и ещё эта огромная часть собственно истории. Нужно написать что-то обобщающее, не вдаваясь в детали. Alexander Mayorov 22:21, 29 октября 2012 (UTC)

Хорошо, перенесу тогда этот текст с оформлением. А куда вы предлагаете поставить вопросы образования арифметических понятий (текущий первый абзац). Вы в нём увидели историю, я же в нём вижу становление арифметических понятий у детей. По меньшей мере принципы нумерации должны быть представлены в начале статьи, потому как к ним идёт отсылка по тексту (из сложения, например). Zanka 23:25, 29 октября 2012 (UTC)

Не относящиеся к теме статьи вопрос рассматривать в конце. Если отсылка в разделе сложение, то написать лучше в одном месте. Alexander Mayorov 07:45, 30 октября 2012 (UTC)

Вставила текст, убрала лишнее из раздела (кое-что совсем, кое-что в соседние разделы). Планирую здесь же добавить операции возведения в степень и извлечение корня, формулы для законов. Как вы думаете: Куда лучше поместить деление с остатком (и надо ли) и основную теорему арифметики? Zanka 18:36, 30 октября 2012 (UTC)

Ну если это к арифметике не относится, то не надо включать (я так и знал, что при делении без остатка на пальцах рубили лишнее, поэтому все древние математики при использовании пальцев для счёта останавливались на сложении и вычитании). Теперь без психологии стало лучше. Alexander Mayorov 19:25, 30 октября 2012 (UTC)

В статье написаны два латинских названия, substractio и subtractio. Думаю, надо оставить какое-то одно (подозреваю, что второе).—Kov 18:42, 28 октября 2012 (UTC)

Спасибо, исправлено. Zanka 20:41, 28 октября 2012 (UTC)

обозначения a, b и так далее[править код]

В статье по арифметике не являются ли неуместными обобщающие обозначения чисел буквами, которые, вроде бы, прерогатива уже алгебры? —Nashev 21:19, 7 апреля 2013 (UTC)

По-другому никак не скажешь, так и в источниках. —Zanka 22:58, 7 апреля 2013 (UTC)

Источники смешивают в своих целях с арифметикой алгебру, и не сильно отделяют от арифметики теорию чисел. Вряд ли есть хоть один источник, ну, кроме совсем уж древних, посвящённый арифметике в чистом виде и не касающийся начал алгебраического анализа. Но у нас тут другие цели — мы пишем статью про арифметику в чистом виде, посему для чистоты можно попробовать…

Вот, например, первый из абзацев с буквенными обозначениями в примере:

Для натуральных чисел естественным образом определены операции сложения и умножения. При объединении двух наборов, содержащих некоторое количество предметов, новый набор будет иметь столько предметов, сколько было в первых двух наборах в сумме. Если первый набор содержал a{\displaystyle a} предметов, а второй — b{\displaystyle b} предметов, то их сумма будет содержать a+b=c{\displaystyle a+b=c} предметов. Указанное действие носит название сложение, определяется символом «+» и является простейшей бинарной операцией. Вообще говоря, таблицу сложения знать не обязательно, достаточно осуществить пересчёт. Последовательное сложение элементов нескольких одинаковых множеств не зависит от порядка этих множеств, что позволило определить другую бинарную операцию — умножение. Помимо умножения в древности существовало отдельное арифметическое действие — удвоение, или умножение на два.

Можно попробовать написать просто с числами:

Для натуральных чисел естественным образом определены операции сложения и умножения. При объединении двух наборов, содержащих некоторое количество предметов, новый набор будет иметь столько предметов, сколько было в первых двух наборах вместе. Если первый набор содержал 3 предмета, а второй — 2 предмета, то их сумма будет содержать 2+3=5{\displaystyle 2+3=5} предметов. Указанное действие носит название сложение, обозначается символом «+» и является простейшей бинарной операцией. Таблицу сложения знать не обязательно, достаточно пересчитать объекты вместе. Последовательное сложение элементов нескольких одинаковых множеств не зависит от порядка этих множеств, что позволило определить другую бинарную операцию — умножение. Помимо умножения в древности существовало отдельное арифметическое действие — удвоение, или умножение на два.

кстати, «в сумме» — это там что? Авторекурсивное определение суммы? Думаю, написать «вместе» будет корректнее… И «определяется символом» странно звучит. Написал «обозначается». «Осуществить пересчёт» тоже подправить тянет. —Nashev 13:45, 8 апреля 2013 (UTC)

Правьте смело! Насколько я вижу, поправить нужно ещё простейшее определение вычитания. Дальше без букв не обойтись, да и в теоретической арифметики сделана оговорка, что используется алгебраический аппарат. —Zanka 14:19, 8 апреля 2013 (UTC)

Посмотрите внимательно ваши правки: 1. иллюстрации нагромождены и портят визуальный ряд, кроме того они другого качества и в другом стиле. 2. Раньше раздел плавно подводил к стеоретической арифметике (правда потом я туда практическую воткнула), но всё же была изначальная логика. Теперь описание выглядит сумбурно. Если вы посмотрите историю правок (но это нудно, так что поверьте на слово), я эти операции тусовала в разном порядке неоднократно. В каждом варианте есть свои плюсы и минусы. Мой последний вариант казался мне наиболее сбалансированным. В общем не торопитесь в ваших правках, статья всё-таки уже со статусом. —Zanka 17:04, 8 апреля 2013 (UTC)

ну, иллюстрации я ставил чтобы как-раз друг на друга не громоздились, и текст читабельным был — в частности, по очереди ставил их слева-справа. Логику тоже «выровнял» — сложение у умножение с их правилами, затем обратные им операции с их расширениями видов чисел, затем всякие более крутые операции с их собственными расширениями. Мне так кажется сбалансированнее. Уверены, что у Вас «глаз не замылился» на этот счёт во время всех тех перестановок? Это действительно непростой труд, и вполне может приводить к разным странностям… —Nashev 17:30, 8 апреля 2013 (UTC)

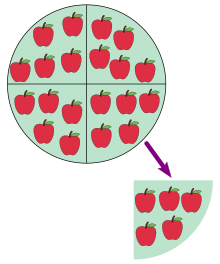
Некоторые абзацы получились короткими, если бы их схлопнуть … Картинка про деление такая мне больше нравится, она в стиле, может поменяете? Ещё бы такой пересчёт найти. —Zanka 17:49, 8 апреля 2013 (UTC)

Во что Вы меня втянули?! 😉 Я уже второй рабочий день на этот подраздел убил %). Авось, не зря. 🙂 —Nashev 15:59, 9 апреля 2013 (UTC)

Я полтора года на эту стать убила. Прочитайте теперь целиком, у вас появились повторы, скачки, стилистика добавленного резко выделяется. Везде стоит добавочка «в алгебраической форме», иногда по два раза на одну формулу. Сделайте так, чтобы викиссылок на перенаправления было меньше (я зелень не люблю). —Zanka 16:24, 9 апреля 2013 (UTC)

Зелень включил, увидел и почистил (кста, мож Вам лучше выключить подсветку, раз не любите? ;). Дубль про алгебраическую форму убрал, остальные по нисходящей там — ИМХО, не мешают и полезны. Стилистику не различаю уже, так что, похоже, не исправлю. Руки убрал, больше правок здесь в ближайшее время делать не буду. Теперь Вы правьте смело, если ещё не надоело 😉 —Nashev 16:51, 9 апреля 2013 (UTC)

Кстати, о каком пересчёте речь? Я картинки с яблочками и персиками перерисовывал, скачав Inkscape и подрезав Notepad-ом вступление в ранее выложенных в викисклад SVG, чтоб они в Inkscape открывались. Можно и пересчёт из них в Inkscape собрать, что бы это ни было… Хотите, научу? —Nashev 17:07, 9 апреля 2013 (UTC)

Уже не надо, я про картинку к натуральным числам (которая первая была), вы её уже перерисовали. По поводу Inkscapeт — спасибо не надо, не хочу голову лишним забивать. Но буду иметь ввиду, что вы умеете :). Если вы закончили, то я посмотрю, но быстро не обещаю. —Zanka 21:15, 9 апреля 2013 (UTC)

Деятельность арифметики[править код]

И кстати, по введению: арифметика (не высшая) числа изучает разве? В смысле, она их природу анализирует? —Nashev 13:45, 8 апреля 2013 (UTC)

Ну а как же аксиоматика? Все эти натуральные-целые-рациональные-вещественные-комплексные… —Zanka 14:20, 8 апреля 2013 (UTC)

Ну, она ж их не анализирует, а постулирует и использует, грубо говоря… —Nashev 17:49, 8 апреля 2013 (UTC)

Согласно источникам, изучение самого процесса развития понятия числа также относится к арифметике. Это особенно заметно, если смотреть статьи больших энциклопедий: общие фразы вначале, потом большой исторический очерк, потом аксиомы Пеано. Разумеется вся конструкция включает высшую арифметику, то есть теорию чисел и иногда вопросы логики применительно к системе аксиом арифметики, то есть формальную арифметику. —Zanka 18:07, 8 апреля 2013 (UTC)

А куда из статьи делось то прекрасное вступление, которое тут в закрытом разделе дано Вами перед вопросом «это то что вы хотели?»? —Nashev 16:05, 9 апреля 2013 (UTC)

Оно в разделе Предмет арифметики 🙂 Не похоже? —Zanka 21:12, 9 апреля 2013 (UTC)

Неа, не очень… Она бывала в перамбуле? Я б практически без изменений её в преамбуле хотел бы видеть, вместо того что там сейчас… —Nashev 22:28, 9 апреля 2013 (UTC)

Нет, в преамбуле она не была. Не забывайте, что часть статьи до содержания — это короткая выжимка со всей статьи. Первый абзац введения сейчас говорит именно о предмете, перечисляя элементарную, теоретическую, высшую, формальную. Далее во введении идёт история, но она объясняет применение прикладных вещей, а также переход к аксиоматике, плюс частично философия, то есть всё, что потом будет в статье подробно. В последнем абзаце упоминается образование: ему в статье отведён раздел. Всё по делу. —Zanka 00:33, 10 апреля 2013 (UTC)

Хм… Часть статьи до содержания не должна быть краткой выжимкой из статьи. Она должна давать самую важную информацию о предмете статьи. Основную, а не по чуть-чуть из каждой. Это разные вещи. По чуть-чуть из каждой, вообще говоря, само оглавление часто лучше даёт. Если соберусь с решимостью заняться переупорядочиванием вступления и предмета, обязательно из этих трёх блоков соберу два на свой вкус. Но это не сегодня точно… —Nashev 13:53, 10 апреля 2013 (UTC)

Может, не настаиваю, это следует упомянуть, что остаток от целочисленного деления на n называется взятием числа по модулю n? (наши секунды и минуты в изображении времени по модулю 60). Д.Ильин 09:53, 8 апреля 2013 (UTC).

А есть предложение куда это добавить? Просто сейчас деление с остатком, если я правильно помню, упоминается как одна из арифметических операций прошлого, туда добавлять некорректно. Добавить к простому определению деления — резкий скачок в сложность, в теоретическую арифметику — выбивается из картины. Я подумаю, идея статьи — показать, что арифметика — это не просто четыре арифметических действия. —Zanka 14:14, 8 апреля 2013 (UTC)

Дело в том, что в высокоуровневых языках программирования термин «остаток от целочисленного деления» не используется, всегда «по модулю», например: mod(i, n) или i\n, а некоторые прикладные программы буквально испещрены этими модулями индексов массивов (оперирующие с кольцевыми регистрами, тороидальными двумерными массивами, БПФ на окне и др.). Думаю, начинающим полезно знать про модуль, что это синоним «остаток целочисленного деления». С уважением, Д.Ильин 07:13, 9 апреля 2013 (UTC).

Может тогда этот модуль и добавить в компьютерную арифметику? А тот, который «абсолютная величина», можно либо к вычитанию, либо к правилу знаков у умножения. —Zanka 14:16, 9 апреля 2013 (UTC)

Уже добавил вскользь к делению, вспомнив про деление с остатком. —Nashev 15:57, 9 апреля 2013 (UTC)

Некоторая неоднозначность «модуль числа» в русском языке. Модуль х по n не есть abs(x) — тоже модуль, нужно подчеркнуть, если вообще то будет в статье. Д.Ильин 07:47, 9 апреля 2013 (UTC).

А как получилось, что они одним словом называются? Вот корни арифметические оказались вполне себе корнями уравнения, хоть и, по историческим причинам, вполне конкретного — степенного. А модули и деление по модулю как связаны? —Nashev 11:17, 9 апреля 2013 (UTC)

Когда появился в математических работах на русском языке термин «модуль» — требует исторического исследования, когда расщепилось это понятие на «абсолютную величину» и «модуль по n» также тема истории математики. Мне труднодоступны работы историков математики позапрошлого века. У современных историков математики ничего по этой теме не нашел, вероятно потому, что лениво искал. Д.Ильин 12:25, 9 апреля 2013 (UTC).

Ошибка с генерацией PDF файла[править код]

Пожалуйста, обратите внимание на это обсуждение. Stannic 17:46, 26 октября 2015 (UTC)

Не возможно сохранить и скачать страницу как PDF файл.

Автор сообщения: 46.200.245.0 06:03, 19 октября 2015 (UTC)

Подтверждаю, именно эта страница почему-то не скачивается.—Valdis72 21:14, 20 октября 2015 (UTC)

А не может ли это быть связано с многократным использованием на странице оператора <math>? —Гдеёж?-здесь 06:00, 23 октября 2015 (UTC)

• Подтверждаю ошибку, по-моему, User:Гдеёж? прав насчёт тегов math. При попытке сгенерировать PDF выводится малопонятное сообщение:

Создание файла не выполнено
Создание файла документа не удалось.
Статус: Rendering process died with non zero code: 1
Возврат к Арифметика

Я попытался скопировать текст страницы к себе в черновик и получил сообщение о том, что адрес academic точка ru включён в чёрный список. Чтобы сохранить страницу, пришлось заменить адрес на несуществующий. Черновик сохранился, но PDF всё равно не генерируется с той же ошибкой. Полная замена всех тегов math на пары <code><nowiki></nowiki></code> «решила» проблему (файл генерируется, скачивается 1,3 MB, читается, всё вроде на месте, кроме формул; вместо формул — их исходный код). Отменил удаление тегов math, ссылок на портал и шаблонов; изменил в двух местах подозрительные теги. Но файл снова не генерируется с той же ошибкой.

Похоже, что действительно дело в слишком большом числе вставок через теги math (кнопкой «Поиск и замена» насчиталось 171 вхождение). Или с числом вставок всё в порядке, но где-то в формуле закралась опечатка. Ещё заметил, что некоторые пары тегов math пустые. Поскольку статья избранная и правка может вызвать возражения, даже если решит проблему, не стану сам лезть чинить, но, видимо, нужно удалить какую-то (существенную) часть тегов math, заменив их на html-разметку. Не понимаю, зачем подряд обрамлять тегами math перечисленные через запятую числа и даже отдельные числа, но, возможно, в этом есть смысл. Stannic 17:40, 26 октября 2015 (UTC)

Пустые тэги я убрала, числа в математической статье должны выглядеть как числа, поэтому даже в тексте я предпочитаю использовать шаблон. Ссылки на академик постараюсь убрать в ближайшее время. Всё равно основной источник БСЭ оффлайн. —Zanka 00:44, 27 октября 2015 (UTC)

• Теперь у меня PDF генерируется, похоже дело было в пустых парах <math></math>.
• Врезка «Боэций об арифметике» в PDF-файле вышла неудачно — заголовок в первом столбце, сам текст во втором, нет выделения. Впрочем, это скорее вина не статьи, а механизма создания PDF.
• Мелочь, но в предложении «Обычно это пальцы на двух руках (основание равно 10), но в исторических источниках встречаются группировки по 5, 11, 12, 20, 40, 60, 80.» после чисел 10 и 80 в PDF-файле видны пробелы. Примерно так: (основание равно 10 ) и 40, 60, 80 . Такие пробелы (после закрывающего тега </math> и перед знаком препинания, скобкой или сноской) заметил ещё в нескольких местах по тексту статьи; минимум в одном месте сноска переходит на следующую строку (сноска 14 в разделе «Исторический очерк» после 1,2,4,8,16). При чтении статьи через браузер таких пробелов нет.
• На 4-5 страницах PDF (раздел «Вычитание: отрицательные числа») фраза «записывается в виде 5−2=3{\displaystyle 5-2=3}» ещё на 4 странице, а точка в конце фразы перескочила уже на 5 страницу.
• В разделе про переместительные законы (возможно, где-то ещё) у формул, стоящих на отдельной строке, в PDF-файле неодинаковые отступы — некоторые с отступом, некоторые без. В браузере как будто отступы одинаковые.
• В разделе «Точные методы» длинная формула вылезает вправо за пределы видимости. Непосредственно перед этим другая формула переносится на новую строку. Stannic 06:55, 27 октября 2015 (UTC)

К обсуждению Stannic 07:57, 27 октября 2015 (UTC)

Аксиоматическое построение арифметики[править код]

Статья совершенно не касается этого важного подхода к теории чисел, хотя этот подход (особенно после после результатов Гёделя) вскрыл глубинную сложность обоснования теории чисел и математики в целом (в частности, вопросы неполноты и непротиворечивости), что обедняет содержание этой статьи. Gnivic (обс) 01:28, 13 июня 2016 (UTC)

Вы не заметили раздел «Формальная арифметика». Хотя название раздела не очень удачно, лучше было бы назвать его именно «Аксиоматическое построение арифметики». LGB (обс) 12:06, 13 июня 2016 (UTC)

Господа, если уйти от сложной патетики Ваших, то, на самом деле я бы не хотела, чтобы мой сын прочитал в Википедии это…арифметика — «понятие числа в развитии представлений о нём». Простите что это? Ребенок, например, отрыл Википедию и сразу же понял, что такое «понятие числа в развитии представлений о нём». Вы же не только для себя пишите — Эта реплика добавлена с IP 93.74.162.161 (о) 22:31, 26 января 2018 (UTC).