Пальцевый счёт — Википедия
Пальцевый счёт, счёт на пальцах или дактилономия — математические вычисления, осуществляемые человеком с помощью сгибания, разгибания или указывания пальцев рук (иногда и ног). Пальцы рук считаются самым первым счётным инструментом древнего человека с эпохи верхнего палеолита. Счёт на пальцах широко применялся в древнем мире и в средневековье, в настоящее время используется ограниченно, арабскими и индийскими торговцами на Среднем Востоке,[1] в европейских странах — в примитивном виде преимущественно детьми или для отображения цифр жестами, ради убедительности в споре по мере перечисления аргументов, а также рефери в боксе при отсчёте секунд во время нокдауна[2].
Создание числовой последовательности[править | править код]
Пальцы рук и ног дали человеку первую числовую последовательность, которая полностью отделилась от считаемых объектов. Будучи разделены на дифференцируемые группы природой, числа сформировали следующие разряды: 5 — пальцев на одной руке, 10 — пальцы на двух руках, 20 — все пальцы рук и ног. Это нашло своё отражение в названиях чисел в языках некоторых народов: пять — «одна рука»
Включение пальцев рук и ног определило создание двадцатичной системы счисления у цивилизации майя в Новом Свете (при этом существовала структура в виде четырёх блоков по пять цифр, что соответствовало пяти пальцам руки и ноги), а ограничение исчисления пальцами рук привело к формированию десятичной системы счисления, возобладавшей у народов Евразии. Пятеричная система, взявшая за основу пальцы одной руки, распространилась в тропической Африке. Двадцатеричная система счисления в Старом Свете была традиционной у чукчей, до настоящего времени используется в названии чисел в нахских языках, а в качестве языкового пережитка оставила след во французском слове «quatre-vingts» («восемьдесят»: буквально — «четырежды двадцать»)[4].
Самое раннее упоминание о десятичной системе пальцевого счёта в литературе содержится у Публия Овидия Назона в книге «Фасты», где автор поэтически отобразил представление древних римлян о числе пальцев рук, которые были увязаны с десятью лунными месяцами женской беременности[1].
Другой весьма распространённый в древности вариант — счёт четвёрками пальцев, при этом счёте большой палец не засчитывался. Так, в древнерусском языке все пальцы, кроме большого, назывались словом «пьрстъ», а большой — «пальць», в английском языке до настоящего времени четыре «счётных» пальца именуются словом «fingers», а большой палец — «thumb». В этом исчислении пальцы двух рук составляют основу древней восьмеричной системы счисления (отличается от современной)[2].
Кроме того на четырёх пальцах одной руки 12 фаланг, если их считать пятым, большим пальцем, то есть прикосновение кончика большого пальца к каждой фаланге принимать за единицу[5]. Эта особенность повлияла на появление двенадцатиричной и шестидесятиричной систем счисления (во втором случае, большой палец несколько раз подряд касался всех фаланг и счёт продолжался дальше, но после каждого нового цикла касаний загибался один палец на второй руке).[6][7]
Римский счёт[править | править код]
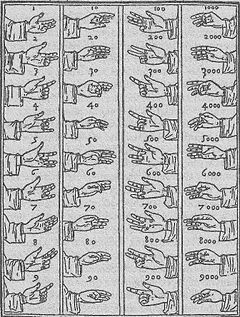Распространённый в средневековой Европе и на Ближнем Востоке пальцевый счёт (из книги «Сумма арифметики» итальянского математика Луки Пачоли, 1494 г.) Отличается от пальцевого счёта Беды Достопочтенного (725 г.) тем, что сотни и тысячи здесь показаны на правой руке, как в древнеримском счёте 
Крупные числа, показанные пальцевым счётом Беды (из книги «Арифметическо-геометрический театр» Якоба Леопольда, 1727 г.)В состав Римской республики, а позднее — империи, входило множество народов, а сфера торговли охватывала всё Средиземноморье и страны Ближнего Востока, имеющие разную счётную письменность или не имеющие таковой. Как результат, возникла весьма развитая, и главное, работающая, система счёта на пальцах, при которой торговцы могли оперировать числами до 10.000 с помощью одних только пальцев двух рук, и до 1.000.000.000, задействуя другие части тела.
Плиний Старший (23-79 гг.) и Макробий (V в.) оставили описания римской статуи бога Януса, которого многие горожане считали также богом Солнца, поскольку пальцы этой статуи изображали число 300 на правой руке и число 65 — на левой: всего 365, что означало количество дней в году, на протяжении которых Солнце совершало свой годичный круг по небосводу. Римский историк Ювенал (ум. ок. 130 г.), рассказывая о мудром старце Несторе, осаждавшем среди прочих греческих героев Трою, между прочим свидетельствует, что пальцы правой руки изображают сотни (и счастлив тот из людей, кто смог обмануть смерть и может показать свой возраст на правой руке). Квинтилиан (ум. ок 96 г.) говорит, что необразованного человека прежде всего выдаёт неумение правильно показать числа на пальцах. Вероятно для неизвестной римской игры использовались комплекты жетонов из слоновой кости по 15 штук каждый, на одной стороне жетона стояла римская буквенная нумерация, а на другой было нанесено изображение руки, показывающей это число особым жестом. Всеобщее знание пальцевого счёта образованными людьми Римской империи подтверждается и трудами ранних отцов Церкви, которые с помощью символики числовых жестов толковали Евангелие, считая, что их читатели прекрасно понимают, о чём идёт речь, и не нуждаются в специальных пояснениях. Так, святой Иероним (342—419/420 гг.), комментируя притчу Иисуса Христа о сеятеле и семенах, которые, упав в добрую почву, дали зерна — «одни — сотню, другие — шестьдесят, а третьи — тридцать», в качестве растолкования привлекает форму жестов римского пальцевого счёта как самоочевидного для всех (хотя к раввинским традициям она отношения и не имеет):
Эта система древнеримского счёта перешла в средневековую Европу, первая реконструкция пальцевого счёта, была впервые подробно изложена в капитальном труде по хронологии «De temporum ratione» английского учёного монаха Беды Достопочтенного в 725 году. По свидетельству Валафрида Страбо, аббата монастыря в Рейхенау на Бодензее, изучавшем арифметику летом 922 года под руководством Татто, великовозрастных учеников учили искусству счёта по пальцевой методике, изложенной в вышеназванной книге Беды. В это время малоиспользуемый в торговле пальцевый счёт занял своё место в учёных кабинетах и школах для духовенства. Об исчезновении счёта на пальцах из повседневного светского обихода как о свершившемся факте говорит знаменитый проповедник Бертольд Регенсбургский (1220—1272 гг.). Считать на пальцах умел всесторонне образованный император Фридрих II Гогенштауфен (ум. 1250 г.). Первой средневековой светской книгой, в которой вновь возрождается интерес к пальцевому счёту и приводится его подробное описание, становится трактат «Сумма арифметики, геометрических пропорций и соразмерности» итальянского математика Луки Пачоли, отпечатанный типографским способом в Венеции в 1494 году. В трактате утверждалось, что пальцевый счёт в то время имел огромное значение в математической науке. В книге «Абака и старинный обычай древних латинян считать с помощью рук и пальцев», изданной в Нюрнберге в 1522 году немецкий писатель Аветин использует пальцевый счёт как вспомогательный для фиксирования промежуточных результатов расчётов на абаке. О том же применении счёта на пальцах, но в сочетании с арабскими (индийскими) цифрами в своё время говорил и итальянский математик Леонардо Пизанский (1180—1250 гг.), утверждая, что тот, кто хочет в совершенстве овладеть искусством вычислений, должен выучится считать на пальцах. Однако с распространением в Европе в XVI веке новых арабских (индийских) цифр, вычисления которыми были удобны на бумаге, пальцевый счёт стал исчезать. Последним произведением, в котором подробно описывался пальцевый счёт в качестве исторического курьёза, стал
Арабско-восточноафриканский счёт[править | править код]
В течение длительного времени на территории Арабского халифата и стран, возникших после его распада, в торговых операциях использовался римский пальцевый счёт, ещё в XIV веке арабские и персидские документы свидетельствуют о хорошем знании арабами римской системы счёта, сходной с той, которая была записана Бедой Достопочтенным в Европе начала VIII века. Особенностью этого счисления стала смена рук, означающих десятки и сотни, в соответствии с системой арабского письма справа-налево. Таким образом, правая рука стала означать сотни, а левая — единицы и десятки. Впоследствии, на восточных базарах и в портах Красного моря и восточного побережья Африки, торговцы выработали собственный оригинальный математический язык жестов. Покупатель и продавец, во избежание нечистоплотных посредников, конкурентов и нежелательных свидетелей, тайно договариваются о цене, накрыв свои руки тканью и касаясь ладоней друг друга по определённым правилам. [1]
Прикосновение к вытянутому указательному пальцу продавца, в зависимости от цены и используемых денежных единиц, будет означать 1, 10 или 100. Одновременное прикосновение к двум, трём или чётырём пальцам продавца будет означать соответственно 2 (20, 200), 3 (30, 300) или 4 (40, 400). Касание открытой ладонью указывает на число 5, 50 или 500. Дотронуться до мизинца означает 6, 60 или 600, безымянный палец — 7, 70 или 700, средний палец — 8, 80 или 800, согнуть указательный палец — 9, 90 или 900, коснуться Большого пальца — 10, 100 или 1000. При этом счислении может соблюдаться последовательность числовых степеней, например число 78 задаётся касанием безымянного пальца продавца, а затем — его среднего пальца. Постукивание по указательному пальцу продавца в направлении от среднего сустава к кончику пальца — предложение о снижении цены вдвое (1/2), на четверть (1/4) или на восьмую часть (1/8) от первоначальной. Постукивание по указательному пальцу от основания пальца до его среднего сустава — будет являться надбавкой половины (1/2) от предложенной цены, или 1/4, или 1/8. Если перед указанием дробной степени указывается целое число, то оно умножается на дробную степень.
Китайский счёт[править | править код]
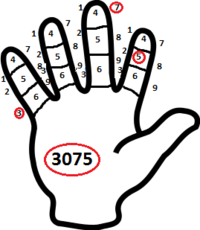Китайская позиционная десятичная система счёта с примером (выделено красным)Китайский метод счёта основан на количестве и символике пальцев. Используя этот метод, на двух руках можно посчитать до 20. Стоит заметить, что в некоторых провинциях жесты могут отличаться.
- 0 — сложенный кулак;
- 1 — разжатый указательный палец;
- 2 — разжаты и растопырены указательный и средний пальцы;
- 3 — разжаты и растопырены указательный, средний и безымянный пальцы;[8]
- 4 — кроме прижатого к ладони большого пальца, остальные разжаты;
- 5 — открытая ладонь;
- 6 — выпрямлены мизинец и большой палец, остальные — сжаты в кулак;
- 7 — большой палец вместе с указательным и средним сложены в щепоть;
- 8 — выпрямлены указательный и большой пальцы, остальные — сжаты в кулак;
- 9 — указательный и большой изогнуты в виде буквы «С», остальные — сжаты в кулак;
- 10 — три варианта. Первый: рука сжимается в кулак; второй: указательные пальцы обеих рук пересекаются; третий: выпрямленный средний палец заводится за выпрямленный указательный, остальные — сжаты в кулак.
Древнекитайская позиционная десятичная система счёта по двум рукам является наиболее сложной из существующих подобных, но при всём том позволяет показать числа от 1 до 99 999 999. На обеих руках фалангам каждого пальца задаются цифровые значения от 1 до 9: причём задействуется пространство как посреди фаланги, так и по бокам. Роль указателя играют ногти больших пальцев. Каждый палец имеет собственную разрядность, как на абаке: указательный палец правой руки — означает единицы, средний палец — десятки, безымянный — сотни и т. д. Переход от пальца к пальцу характеризуется последовательным повышением разряда. Пропуск имеет значение нуля[2].
Японский счёт[править | править код]
В Японии счёт начинается с открытой ладони. Поджатый большой палец представляет число 1, мизинец является числом 5. Таким образом, пальцы, сложенные в кулак, указывает на число 5. Затем совершается обратное действие: число 6 обозначается разжатым мизинцем. Возврат к открытой ладони означает число 10. Однако, чтобы показать цифры другим собеседникам, используется тот же порядок, что в английской или русской традиции: выпрямленный указательный палец становится номером 1, большой палец теперь представляет число 5. Для чисел свыше пяти соответствующее количество выпрямленных пальцев другой руки прижимаются к раскрытой ладони первой. Например, число 7 отображают указательный и средний палец. Число 10 изображается двумя раскрытыми к собеседнику ладонями[9].
Английский счёт[править | править код]
В англоязычных странах счёт до 5 ведётся разжатием пальцев, первоначально собранных в кулак, начиная с указательного пальца, и продолжается до мизинца (число 4). Разжатый большой палец указывает на число 5. Аналогичным образом процесс счёта продолжается на другой руке для чисел от 6 до 10. Например, число 7 указывается открытой ладонью с растопыренными пальцами одной руки и разжатыми указательным и средним пальцами другой. Чтобы указать на количество своему собеседнику, коренной житель англоговорящей страны поднимает руку или руки вверх. Например, разжатые указательный, средний и безымянный пальцы на поднятой вверх ладони будут означать число 3[10].
Балканские страны на юго-востоке Европы имеют счёт, схожий с английским.
Континентальный европейский счёт[править | править код]
У народов континентальной Западной Европы, таких, как немцы или французы, разжатый большой палец представляет собой начало исчисления (число 1). Затем разжимается указательный палец (число 2) и так далее — до мизинца (число 5)[10].[11]
В некоторых европейских странах, а зачастую и во Франции, альтернативный метод подсчёта проводится путём сгибания пальцев в порядке: большой, указательный, средний, безымянный и мизинец.
Русский счёт[править | править код]
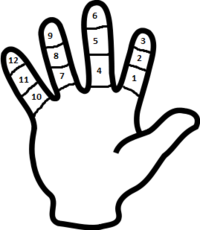«Счёт дюжинами» 
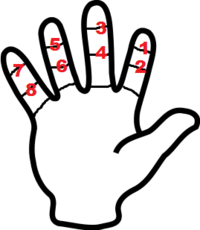«Счёт сороками»Русский счёт на пальцах до десяти начинается с загибания мизинца левой руки и последовательно ведётся до загнутого большого пальца правой руки. Но когда требуется наглядно показать количество, рука сжимается в кулак и сначала разжимается указательный палец, затем средний, безымянный, мизинец и большой[2].
Этот счёт также имеет место в странах бывшего СССР.
Старинный русский способ умножения на пальцах однозначных чисел от 6 до 9 издревле применялся купцами как вспомогательный при устном счёте. Первоначально пальцы обеих рук сжимали в кулаки. Затем на одной руке разгибали столько пальцев, на сколько первый множитель превосходит число 5, а на второй руке делали то же самое для второго множителя. Суммарное число вытянутых пальцев умножалось на 10, потом перемножалось число загнутых пальцев одной руки на число загнутых пальцев другой. Два полученных результата складывались[2].
Из других способов счисления по пальцам был распространён «счёт дюжинами» (двенадцатеричная система), употреблявшийся в торговле (особенно в Новгородской республике XII—XV веков). Счет дюжинами вёлся большим пальцем по фалангам остальных четырёх пальцев правой руки и начинался от нижней фаланги указательного пальца, а заканчивался верхней фалангой мизинца. Другой вариант — от верхней фаланги мизинца левой руки до нижней фаланги указательного пальца. Если число превышало 12, то при достижении 12 считающий загибал один палец на противоположной руке. По достижении числа 60 (пятёрки дюжин) все пальцы руки, фиксировавшей полные дюжины, оказывались сжатыми в кулак. Дюжинами до начала XX века в России было принято считать носовые платки, пишущие перья, карандаши, школьные тетрадки, набор из 12 предметов по традиции составляли ложки, вилки, ножи, а посудные сервизы и комплекты стульев и кресел рассчитывались на 12 персон (что оставило след в названии романа «Двенадцать стульев»)[2].
Но наибольшее распространение в Древней Руси получил «счёт сороками» («сороковицами»). Охотники за пушным зверем в Сибири вели счет «сорочками», то есть укомплектованными в мешки шкурками (как правило, 40 собольих хвостов или 40 беличьих шкурок), которые полностью уходили на пошив богатой шубы («сорочки») русского боярина XVI века. Так, в таможенной грамоте 1586 года «сороками» были посчитаны шкурки соболей и куниц, посланные в качестве платы за ведение войны с турками от царя Фёдора Ивановича австрийскому императору Рудольфу. Методика счёта была схожа со «счётом дюжинами», только вместо подсчёта фаланг считали суставы пальцев (переходы между фалангами), которых было всего 8. Если число превышало 8, то при достижении 8 считающий загибал один палец на противоположной руке. По достижении числа 40 все пальцы руки, фиксировавшей полные осьмушки, оказывались сжатыми в кулак. Следы пальцевого «счёта сороками» сохранились в народных суевериях. Например, несчастливым для охотника считался сорок первый медведь и т. д. Также словом «сороконожка» традиционно называлась любая многоножка. Выражение «сорок сороков» или «тьма» для древнерусского крестьянина символизировало некое число, превосходящее всякое воображение и собственно математические познания самого земледельца[2].
Пальцевый счёт в качестве культурной идентификации[править | править код]
Культурные различия в подсчете на пальцах у разных народов иногда используются как тайный пароль, в частности, для различия национальностей во время войны. Эта возможность культурной идентификации является частью сюжета в фильме «Бесславные ублюдки» Квентина Тарантино и в романе «Пи в небе» («Pi in the Sky: Counting, Thinking, and Being»), Джона Барроу[12][13].
Английский писатель Р. Мейсон в книге «А ветер не мог читать» приводит житейский пример из истории Второй мировой войны об японке Сабби, волей судьбы оказавшейся в Индии, принадлежащей тогда Великобритании, которая находилась с Японией в состоянии войны. Когда Сабби представили одному англичанину как китаянку, тот предложил ей сосчитать на пальцах до пяти, после чего обман раскрылся: «Вы видели как она считает? Загибает один за другим пальцы. Вы когда-нибудь видели, чтобы китаец при счёте загибал пальцы? Никогда! Китайцы считают так же, как и англичане. Они поднимают кулак и разгибают пальцы! Она японка!»[1]
В некоторых видах спорта, например в велосипедной гонке «Тур де Франс», перед стартом используется обратный отсчёт от 5 до 1 на пальцах поднятой руки судьи. Числа в этой системе, отображаются следующим образом:
- 5 — разжаты все пальцы, включая большой
- 4 — кроме большого все пальцы разжаты
- 3 — разжаты большой, указательный и средний палец
- 2 — разжаты указательный и средний палец
- 1 — разжат большой или указательный палец
- 0 — все пальцы вытянуты снова, но рука отводится в сторону. Это сигнал о начале гонки.
Одной из самых примитивных систем счёта, является телесный счёт — разновидность пальцевого счёта, задействующая и другие части человеческого тела в определённом порядке. Как правило, первобытные племена, использующие эту разновидность счисления, не имеют в языке достаточного количества слов для обозначения цифр, поэтому те же самые слова могут означать разные цифры и не могут быть верно поняты без содействия жестового языка. Также отсутствует настоящая числовая последовательность, как это имеет место в пятеричной, восьмеричной, десятичной, двенадцатеричной или двадцатичной системах счисления. Так, пальцевая арифметика народности панцах исчерпывается следующими цифрами[1]:
- 1 (ануси) — выпрямленный мизинец правой руки;
- 2 (доро) — выпрямленный безымянный палец правой руки;
- 3 (доро) — выпрямленный средний палец правой руки;
- 4 (доро) — выпрямленный указательный палец правой руки;
- 5 (убеи) — выпрямленный большой палец правой руки;
- 6 (тама) — указывание на правое запястье;
- 7 (унубо) — указывание на правый локоть;
- 8 (виса) — указывание на правое плечо;
- 9 (деноро) — указывание на правое ухо;
- 10 (дити) — указывание на правый глаз;
- 11 (дити) — указывание на левый глаз;
- 12 (медо) — указывание на нос;
- 13 (бее) — указывание на рот;
- 14 (деноро) — указывание на левое ухо;
- 15 (виса) — указывание на левое плечо;
- 16 (унубо) — указывание на левый локоть;
- 17 (тама) — указывание на левое запястье;
- 18 (убеи) — выпрямленный большой палец левой руки;
- 19 (доро) — выпрямленный указательный палец левой руки;
- 20 (доро) — выпрямленный средний палец левой руки;
- 21 (доро) — выпрямленный безымянный палец левой руки;
- 22 (ануси) — выпрямленный мизинец левой руки.
- ↑ 1 2 3 4 5 6 7 8 9 Карл Меннингер «История цифр. Числа, символы, слова», — М: ЗАО Центрполиграф, 2011, С. 49-53, 257—278. ISBN 978-5-9524-4978-7
- ↑ 1 2 3 4 5 6 7 Б. Казаченко «Тридевятое царство, тридесятое государство, или как считали наши предки» // Журнал «Наука и жизнь», № 10, 2007 год.
- ↑ Например: «пядь» — старинная единица измерения, равная ладони (17,78 см), также старорусское слово «пясть» означает ладонь, кисть руки (Владимир Даль «Словарь живого великорусского языка»)
- ↑ В. П. Алексеев, А. И. Першиц «История первобытного общества: учебник для студентов вузов по специальности „История“», — М.: АСТ, 2007, С. 299. ISBN 5-17-022316-1
- ↑ (яп.) Nishikawa, Yoshiaki (2002), ヒマラヤの満月と十二進法 (The Full Moon in the Himalayas and the Duodecimal System), <http://www.kankyok.co.jp/nue/nue11/nue11_01.html>. Проверено 24 марта 2008. Архивная копия от 29 марта 2008 на Wayback Machine
- ↑ (англ.) Ifrah, Georges (2000), The Universal History of Numbers: From prehistory to the invention of the computer., John Wiley and Sons, ISBN 0-471-39340-1
- ↑ (англ.) Macey, Samuel L. The Dynamics of Progress: Time, Method, and Measure (англ.). — Atlanta, Georgia: University of Georgia Press (англ.)русск., 1989. — P. 92. — ISBN 978-0-8203-3796-8.
- ↑ Китайский счет до десяти пальцами одной руки (видео на youtube).
- ↑ (яп.) Namiko Abe. Counting on one’s fingers (яп.). About.com. Дата обращения 12 августа 2012. Архивировано 2 октября 2012 года.
- ↑ 1 2 (англ.) Pika,Simone; Nicoladis, Elena; and Marentette, Paula. How to Order a Beer: Cultural Differences in the Use of Conventional Gestures for Numbers (англ.) // Journal of Cross-Cultural Psychology (англ.)русск. : journal. — 2009. — January (vol. 40, no. 1). — P. 70—80. — DOI:10.1177/0022022108326197.
- ↑ См. также: Французский счёт на пальцах, Compter sur ses doigts (видео на youtube)
- ↑ (англ.) Barrow, John D. Pi in the Sky (неопр.). — Penguin, 1993. — С. 26. — ISBN 978-0140231090.
- ↑ (англ.) Dactylonomy (неопр.). Laputan Logic (16 ноября 2006). Дата обращения 12 августа 2012. Архивировано 2 октября 2012 года.
Воображаемые счёты: сложные вычисления «на пальцах»
Маленькие дети в Южной Азии могут производить сложные математические вычисления за несколько секунд, просто щёлкая пальцами в воздухе.
Их секретный инструмент — воображаемые счёты-абак.
Новости с программы Mind Mathlon 2014, которая проходила в марте в Технологическом институте города Карачи, рассказывали о маленьких детях, которые просто щёлкают пальцами и производят сложнейшие вычисления с невероятной точностью.
Очевидно, детей научили использовать пальцы в качестве бусинок на счётах, что позволило им складывать и вычитать со скоростью калькулятора.
Эта техника довольно проста, но чтобы её освоить, требуется несколько лет практики. Пальцы правой руки — единицы. Поднятый вверх большой палец правой руки — число 5. Каждый палец левой руки соответствует десяткам. А поднятый вверх большой палец левой руки — это число 50. То есть два больших пальца, поднятых вверх — это 55.
Удивительная особенность этой техники в том, что использовать её может любой: слабовидящий ребёнок, участвующий в вышеуказанной программе, считал ничуть не хуже всех остальных. 11-летние дети запросто умножали 10-значные числа и даже извлекали квадратный корень из 6-значного числа, и всё это без калькулятора, карандаша и бумаги.
Ясин Атальф генеральный директор лаборатории робототехники, пояснил, что детей просто научили двигать воображаемые бусинки на воображаемых счётах-абак.
Эта техника популярна среди школьников в ряде азиатских стран, например, в Китае, Японии и Индии.
Майкл Франк из Стенфордского университетаи Дэвид Баннер из Университета Калифорнии отправились в школу в штате Гуджарат в Индии, чтобы понять, как эта техника работает.
В частности специалисты хотели понять, как детям удаётся следить за всеми 15 столбцами воображаемых счёт, в то время как многие люди едва смогут отследить 3 или 4 столбца. Они изучали детей, которые обучались технике только один год. И эти дети не могли выполнять арифметические действия с числами, в которых больше трёх или четырёх знаков. Это означало, что эти дети в состоянии держать в голове лишь три или четыре столбца своих «счёт».
А ещё специалисты установили, что работа на воображаемых счётах не зависит от языковых систем. В других похожих техниках учащимся приходится представлять числа, оперируя их названиями на том или ином языке. А воображаемые счёты-абак — задача полностью визуальная, и от языка никак не зависит.
По словам Альтафа, эта «психическая математика» подойдёт каждому, кто желает отточить свои навыки счёта в уме. Но чтобы добиться действительно впечатляющих результатов, потребуется не один год напряжённой работы.
Китайские педагоги научили детей решать сложнейшие примеры с молниеносной быстротой
Обгонять калькулятор воспитанникам помогают тренировки с незатейливым предметом, хорошо знакомым каждому из нас.
Детские пальцы ловко перебирают пластмассовые косточки. 11 летние девчонки складывают, вычитают и умножают пятизначные числа. Мгновение и ответ готов. Еще один трудный пример, но все расчеты уже в уме. Потом еще сложнее: нужно считать и прыгать через скакалку. Удивительно, но ответ снова верный.
«Взрослые всегда удивляются: я считаю быстрее них! Научиться этому несложно. Нужно просто каждый день тренироваться», — говорит ученица Чжань Сяожань.
Дети считают быстрее, чем калькулятор. Система, по которой их учат в течение 6 лет, называется «менар» или ментальная арифметика.
«Эта система устного счета стара, как мир. Сами счеты появились в глубокой древности. И с тех пор принципиально не изменились. Только называются везде по-разному», — говорит секретарь организации устного счета Ucmas Ван Лигуан (Пекин).
Международное название «Абак». В Китае «суаньпань», в Японии «соробан», а в России русские счеты. Между собой они отличаются только количеством спиц и косточек на них. Сам же принцип работы одинаков. Хорошо забытая старая система счета, как новая заработала в 1993 году в
Азии. А сегодня более 5 тысяч таких школ по всему миру. Исключая Россию.
Русские счеты, аналог римских, появились в начале XVI столетия. Их использовали и в коммерции, и в школе для обучения арифметике. Но в 60-х годах XX века русские счеты, из системы школьного образования исключили. Как устаревший метод.
«Абака, может быть, и развивает устный счет. Но вообще имеет очень маленькое отношение к математике как к науке. Понимаете, математика это логика, это логическое умение решать сложные логические проблемы. Устный счет не заменяет этого», — считает заслуженный учитель РФ, заместитель директора школы Борис Давидович.
Древние счеты год от года становятся все популярнее. Тем не менее, учителя спорят. Преимущество менара над другими системами развития научно не доказано. А современному человеку считать в уме вообще практически не приходится. Но если под рукой калькулятора нет — можно посчитать и самим. В столбик или на счетах, неважно.
Счёт на пальцах: viata — LiveJournal
Римский легионер входит в бар, показывает бармену два пальца и говорит: «Пять бутылок для меня и моих друзей!»Самое забавное в этой шутке, что отчасти она верна: разные народы действительно считают на пальцах по-разному, и древние римляне действительно показывали числа на пальцах иначе, чем мы. Примерно вот так: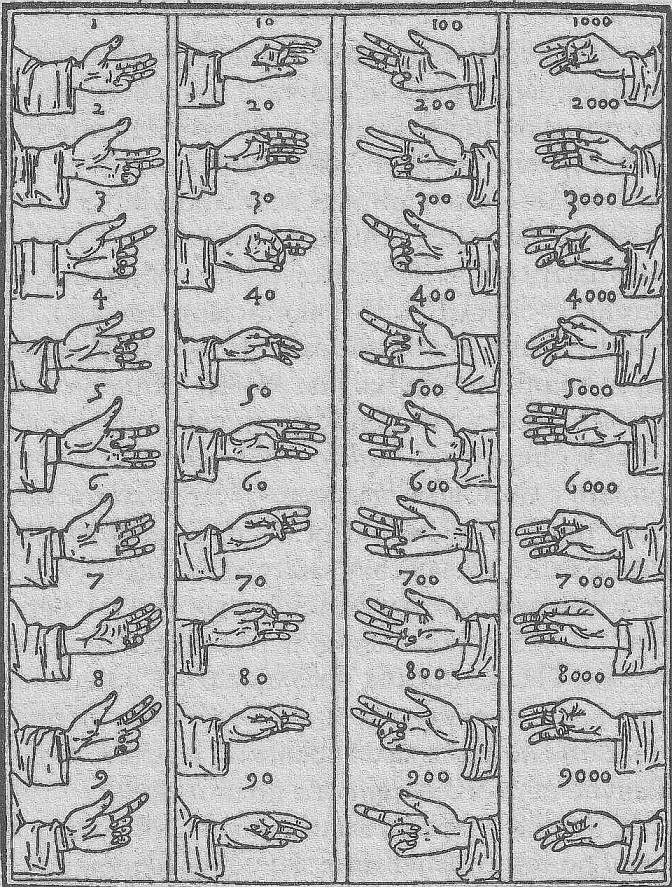
Эта система активно использовалась по всей Европе и Средиземноморью в начале нашей эры и довольно часто упоминается в текстах того времени, а также используется в изобразительном искусстве, когда персонажи картин или статуи показывают те или иные символичные числа.
На основе этой римской системы в средневековой Европе возникла другая, описанная Бедой Достопочтенным:
В арабском мире в ту же эпоху тоже знали европейский пальцевый счёт, но использовали и свой собственный, позволявший договариваться о цене не глядя и незаметно для окружающих, накрыв руку продавца и покупателя. Вот описание этой системы из Википедии:
«Прикосновение к вытянутому указательному пальцу продавца, в зависимости от цены и используемых денежных единиц, будет означать 1, 10 или 100. Одновременное прикосновение к двум, трём или чётырём пальцам продавца будет означать соответственно 2 (20, 200), 3 (30, 300) или 4 (40, 400). Касание открытой ладонью указывает на число 5, 50 или 500. Дотронуться до мизинца означает 6, 60 или 600, безымянный палец — 7, 70 или 700, средний палец — 8, 80 или 800, согнуть указательный палец — 9, 90 или 900, коснуться Большого пальца — 10, 100 или 1000. При этом счислении может соблюдаться последовательность числовых степеней, например число 78 задаётся касанием безымянного пальца продавца, а затем — его среднего пальца. Постукивание по указательному пальцу продавца в направлении от среднего сустава к кончику пальца — предложение о снижении цены вдвое (1/2), на четверть (1/4) или на восьмую часть (1/8) от первоначальной. Постукивание по указательному пальцу от основания пальца до его среднего сустава — будет являться надбавкой половины (1/2) от предложенной цены, или 1/4, или 1/8. Если перед указанием дробной степени указывается целое число, то оно умножается на дробную степень.»
Увы, «пять» ни в одной из этих систем не похоже на соответствующий письменный знак. Зато, например, китайцы и сейчас намекают на иероглифы для соответствующих цифр, когда показывают количество на пальцах.
От одного до пяти они считают так же, как мы (начиная с указательного пальца), за тем исключением, что 3 обычно показывают не указательным, средним и безымянным пальцем, а знаком «окей».
Но самое веселье начинается потом.
Скрещенные пальцы (средний и указательный) при загнутых остальных — Ещё один вариант цифры 10, встречающийся и в Китае, и в Японии. Отсылает, конечно, к тому же иероглифу 十.
И даже если считать простым загибанием пальцев – обратите внимание, что в одной и той же России можно делать это двумя способами: считая загнутые пальцы – или выпрямленные.
Интересно, что каждая система счёта на пальцах кажется пользователям совершенно логичной и разумной, но чем больше таких систем брать, тем больше в них различий. Например, если добавить в эту картину ещё и жестовые языки, то этот знак:
в русском жестовом будет по-прежнему означать 3, а в американском жестовом – уже шесть. А вот китайский жестовый полностью унаследовал все жесты для цифр из обычной китайской традиции.
Из современных систем пальцевого счёта можно упомянуть ещё двенадцатеричную систему, которую продвигают, в частности, два общества, агитирующие за полный переход к двенадцатиричной системе (Dozenal Society of America и Dozenal Society of Great Britain). Аналогичных обществ в других странах мне не известно.
Идея состоит в том, что разным фалангам на пальцах одной руки присваиваются значения, и на эти фаланги можно указывать большим пальцем или другой рукой. Вот так выглядит эта двенадцатиречная рука:
При этом на второй руке можно загибать пальцы по числу полных дюжин. Интересно, что такой счёт, по-видимому, использовался средневековыми новгородцами. Есть версия, что и древними шумерами тоже, но аргумент в её пользу обычно приводят всего один: должны же были шумеры как-то считать на пальцах — почему бы не так.
А вот рука для счёта не восьмёрками, как можно было бы подумать, а сороками:
Когда на второй руке оказываются загнуты все пять пальцев по числу полных восьмёрок, в общей сложности получаем 40.
Но самая сложная из подобных систем существовала в Китае, где тоже указывали на фаланги пальцев, но на каждом пальце были места для девяти цифр, и каждый палец сответствовал разряду. Например, указательный означал единицы.
Чтобы показать 3075 в этой системе, нужно было указать большим пальцем на нужные места мизинца, среднего и указательного пальцев.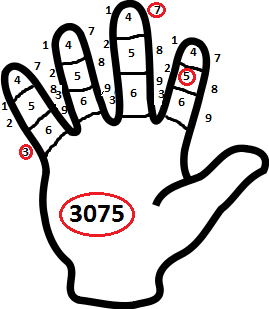
Из новых и ныне здравствующих систем пальцевого счёта стоит назвать бинарную, в которой загнутые и прямые пальцы означают нули и единицы. Такой счёт, понятно, возник с развитием информатики и широко распространён только в узких кругах.
Выглядит это так:
И, конечно, существует множество мнемонических приёмов, позволяющих на пальцах умножать однозначные и двузначные числа на девять, перемножать числа от 6 до 9, переводить из десятичной системы в двоичную и делать много прочего интересного.
| Константин Кноп в ФБ обратил внимание на виральное видео, на котором девочки очень быстро складывают и вычитают в уме трехзначные числа (а также делят и умножают двузначные): https://www.facebook.com/thatscoop/videos/935148249840024/ Вопрос: как они это делают и что они делают пальцами. Насколько я смог разобраться: эта техника называется «ментальные счеты» (mental abacus), и она популярна в последние годы в странах Азии. Вот статья в психологическом журнале о ней: Representing exact number visually using mental abacus. Там рассказывается, что эти дети держат счеты перед собой в уме — два или три разряда, расположенных горизонтально. В каждом разряде вертикально есть от 0 до 4 костяшек, и отдельно костяшка, которая символизирует пятерку. Как вот такие счеты примерно, только они эту картинку целиком держат в уме и «смотрят» на нее во время вычислений: В статье не объясняются странные движения рук девочек на видео. Сначала я думал, что они на пальцах держат какую-то часть информации о текущем числе, и таким образом помогают себе запомнить. Но потом я нашел другое видео, замедлил его в два раза, просмотрел внимательно несколько раз… теперь я убежден, что они руками ДВИГАЮТ КОСТЯШКИ воображаемых счетов. Это помогает, по-видимому, сохранять картинку перед глазами и не путаться в том, как она меняется. Девочки на видео выше делают слишком сложные вычисления, чтобы это ясно разглядеть, но вот на этом видео проще: Правая рука занята разрядом десятков, левая — разрядом единиц. Например это четко видно по движениям девочки на 01:01. Ей говорят: 47 (движутся обе руки, счеты ставятся в правильное положение), +2 (движется только правая рука), +6 (движутся обе руки — нужно сменить десятки тоже), -9 (движутся обе руки), +1 (только правая), и она говорит ответ: 47. Мне кажется, что я понял в общих чертах, как они это делают. Правда, зачем это нужно, все равно остается непонятным. |
Как вы можете посчитать на пальцах рук до 59 000? :: Инфониак
Наука Как вы думаете, до скольких можно посчитать на пальцах ваших обеих рук?
Конечно, большинство ответит, что до 10.
Математик Джеймс Тантон (James Tanton) объясняет, как можно существенно увеличить число, до которого можно дойти, считая только на пальцах рук.
* Более продвинутые люди скажут, что могут на одной руке досчитать до 12-и, так как каждый из 4 пальцев руки можно разделить на 3 секции и считать большими пальцами. На 2-х руках можно досчитать до 24-х.
Читайте также: 10 интересных фактов о числах
* Можно использовать 5 пальцев одной руки, чтобы посчитать, сколько раз мы досчитали до 12 на другой руке. Так как у нас на одной руке 5 пальцев, значит, мы можем посчитать 5 раз до 12, а это значит, что на пальцах можно посчитать до 60-и.
* Но мы знаем, что 4 пальца каждой руки можно разделить на 3 секции, значит можно использовать каждую из 12 секций на одной руке, чтобы посчитать, сколько раз мы досчитали до 12-и на второй руке. Так мы доберемся до 144.
Считаем на пальцах
Дальше больше.
Вот, где начинается самое интересное. Вы можете досчитать на пальцах до еще большего числа, если найдете больше секций на руках.
* Каждый палец имеет 3 секции и 3 сгиба, а значит, на одном пальце мы можем досчитать до 6-ти, а значит на 4-х пальцах можно досчитать до 24-х, а на двух руках до 48-и.
* Если использовать одну руку, чтобы посчитать, сколько раз мы досчитали до 24 на другой руке, то получится 24*24 = 576.
Да, на одном пальце можно досчитать максимум до 6-ти, но это не значит, что мы закончили считать.
Давайте прибегнем к позиционной системе счисления, возникшей в древнем Вавилоне. В этой системе значение цифр в записи числа зависит от разряда данной цифры в числе. Попробуем использовать этот метод, чтобы побить наш рекорд.
Для этого забудем про секции на каждом пальце!
Представьте, что вы можете двигать пальцами только вверх и вниз. С помощью двоичной системы счисления – то есть каждое число в два раза больше предыдущего – а также, если назначить каждому пальцу отдельное значение, можно пойти еще дальше.
Читайте также: Названы самые любимые числа в мире
Посмотрите на изображение. Каждый палец имеет своё значение. Каждый следующий палец равен значению предыдущего пальца, умноженное на 2. Если первый палец 1, то второй будет 1х2=2, третий 2*2=2, четвертый 4х2=8, пятый 8х2=16 и так далее.
Например, вы хотите показать число 7, значит можно поднять 3 пальца со значениями 1,2 и 4 (1+2+4=7).
Или, допустим, вы хотите показать число 250. Вы суммируете: 128+64+32+16+8+2=250. Можно показать это трехзначное число 6-ю поднятыми пальцами.
* Если поднять все пальцы вверх, то получится максимальное число, то есть 1 023 (1+2+4+8+16+32+64+128+256+512).
Давайте пойдем дальше.
Можно согнуть каждый палец наполовину, а значит, у нас получаются 3 позиции: полностью согнутый палец, наполовину согнутый и полностью поднятый.
Теперь можно использовать троичную систему счисления, чтобы досчитать до 59 048.
Взгляните на изображения, чтобы понять значение каждой позиции:
Первый палец имеет значение 2, второй 2х3=6, третий 6х3=18, четвертый 18х3=54, пятый 54х3=162 и так далее.
Если поднять все пальцы, то получается число 59 048.
Ниже вы можете ознакомиться с видео, где математик детально всё объясняет.
Наши компьютеры работают по такому же принципу.
То, как вы считаете на пальцах, может многое рассказать :: Инфониак
Культура Проведите один занимательный эксперимент. Оторвитесь от ваших дел и посчитайте до десяти, используя пальцы. Закончили? Как вы это делали? Вы начали считать с левой или с правой руки? Вы начали считать с большого пальца или с мизинца? А может даже с указательного? Вы начали считать с закрытого кулака или открытой руки?
Если вы европеец, то велики шансы того, что вы начали с закрытого кулака, считали с большого пальца на левой руке. Если вы со Среднего Востока, вы тоже начали со среднего кулака, но начали считать с мизинца на правой руке.
Большинство китайцев и многие североамериканцы также используют систему закрытого кулака, но начинают считать с указательного пальца, а не с большого. Японцы, как правило, начинают с открытой руки, загибая первым мизинец, а затем оставшиеся пальцы.
В Индии, используют сегменты пальцев, чтобы досчитать до 20, а амазонские народы Пира вообще не используют пальцы для того, чтобы подсчитать что-то.
Счет по пальцам кажется нам естественным, как дыхание, но это не врожденная характеристика, и даже не общепринятая. Существует множество техник, и они культурно обусловлены.
Немецкие ученые Андреа Бендер (Andrea Bender) и Сигхард Беллер (Sieghard Beller) утверждают, что изучая технику счета по пальцам, можно лучше понять, как культура влияет на когнитивные процессы, а именно на арифметику, производимую в уме.
Существует умственная связь между руками и цифрами, но эта связь произошла не от того, что люди научились считать, используя руки. Она уходит корнями в эволюцию. Та часть мозга, которая изначально развилась, чтобы представлять наши пальцы, была задействована для того, чтобы представлять наши числа, и сегодня она выполняет обе эти функции.
Сканирование мозга с помощью функциональной магнито-резонансной томографии показало, что области, которые связаны с ощущением пальцев, активизируются, когда мы выполняем задания на счет, даже если мы не используем при этом пальцы. Также исследования показывают, что маленькие дети с хорошим восприятием пальцев лучше выполняют количественные задачи, чем дети с меньшим пониманием пальцев. Даже будучи взрослыми, то, как мы представляем себе цифры в уме, связано с рукой, с которой мы начинаем счет.
Из немецких исследований языка жестов, известно, что тип системы счета по пальцам, который мы используем, влияет на то, как мы мысленно представляем и обрабатываем числа. Возможно, так происходит потому, что это является сенсорно-моторной функцией с прямой связью между движениями тела и активностью мозга.
Так означает ли все то, что мы думаем о числах по-разному, в зависимости от культурных корней?
Возможно. Взять, например евразийскую систему. Она практически буквальна. Один палец равен одному числу и мозг моментально воспринимает эту концепцию. Но в китайской счетной системе по пальцам используются символические жесты, чтобы представить любое число выше пяти. Люди из Папуа-Новой Гвинее используют большую часть верхней части тела для того, чтобы представить числа. Такие жесты нужно выучить и затем извлечь в случае необходимости из рабочей памяти. Это требует больших умственных усилий, но символическая система позволяет и лучше выполнять сложные арифметические действия.
Тут возникает вопрос: может ли быть так, что некоторые люди превосходят других в математике только из-за того, что они живут в другой стране?
Специалисты говорят, что это маловероятно, так как некоторые аспекты счета по пальцам распространены по всему миру, тогда как другие различаются даже в одной культуре. Но они, все же, считают, что практикуя различные техники счета по пальцам, можно улучшить свою умственную арифметику. Пока это не было эмпирически доказано, но ничто не мешает вам попробовать.