03.03.1970

Примеры для абакуса: Ментальная арифметика задания, примеры для решения

Содержание

Ментальная арифметика для детей от 5 до 16 лет • Детский клуб «Классики»

Вы сможете решить этот пример за несколько секунд, без помощи калькулятора?

872+116-761+262-378=?

А ваш ребенок сможет.

Детский клуб «Классики» открывает новое направление – Ментальная Арифметика для детей от 5 до 16 лет.

Что такое ментальная арифметика?

  • Ментальная – значит «мысленная». Ментальная арифметика – вычисления в уме, без помощи калькулятора, тетрадок и других вспомогательных средств
  • Ментальная арифметика зародилась в древнем Китае, а в 21 веке приобрела фантастическую популярность. Завоевав азиатские страны, ментальная арифметика быстро развивается в Европе и Америке. Сейчас во всем мире работает более 5000 школ этого направления.
  • На первом этапе ребенок учится считать при помощи абакуса. Это прибор, похожий на счёты.
  • На следующем этапе дети откладывают настоящие абакусы в сторону и переходят на воображаемые. Теперь они только представляют этот прибор в уме и считают, мысленно передвигая косточки.
  • Как раз в этот момент начинается самая большая польза от занятий. Почему? Сейчас объясним.

Положительный эффект от занятий ментальной арифметикой

Собственно зачем ребенку уметь делать такие сложные вычисления в уме? Ведь удобные калькуляторы есть в любом смартфоне.

Быстрые вычисления в уме – это не самоцель.

Когда дети переходят к работе с «мысленными абакусами», в работу включается воображение, концентрация внимания. То есть, задействуется правое полушарие головного мозга.

В это же время синхронно работает и развивается левое полушарие, отвечающее за логику и счет.

Таким образом мышление ребенка с детства «привыкает» решать жизненные задачи двумя полушариями головного мозга одновременно: сконцентрироваться на вопросе, вообразить какую-то схему и логически решить эту задачу. Очень быстро возникает креативный и в то же время логический подход к решению вопросов.

Итак

  • Ребенок учится делать сложные вычисления в уме и удивлять окружающих.
    Растет его самооценка и уверенность в себе
  • Развивается кратковременная, долговременная и фотографическая память, концентрация внимания, как следствие – повышается успеваемость в школе
  • Ребенок с детства учится решать жизненные задачи, задействуя оба полушария головного мозга сразу: сконцентрировался, вообразил схему решения, быстро нашел креативное и логически обоснованное решение вопроса.

Преимущества нашего курса

  • Все ученики получают доступ к порталу с упражнениями, чтобы ребенок мог тренироваться каждый день самостоятельно по 10 минут, а родитель мог отслеживать прогресс
  • Каждый урок всего курса прописан по минутам. Ученики получают рабочие тетради, в которых к каждому занятию предусмотрено определенное количество упражнений. Преподаватель отпускает ребенка когда убедится, что все они выполнены корректно и ребенок усвоил материал.
  • Стоимость пропущенных занятий не пропадает: мы «перебрасываем» эти деньги на депозит, который можно впоследствии использовать для посещения занятий и мастер-классов творческих направлений.

Результаты детей 5-6 лет:

Через 4 месяца занятий: Дети умеют складывать и вычитать на абакусе двузначные числа, а в уме они считают легкие примеры с двузначными числами и одинаковыми цифрами, например 11+66-55+77 и т.д.

Через 8 месяцев занятий: Дети складывают и вычитают на абакусе двузначные числа, используя несложные формулы, а в уме они решают легкие примеры, такие как 11+66-55+77, 54+45-31-15, и т.д.

Через полтора года занятий: Дети складывают и вычитают на абакусе двузначные и трехзначные числа, переходят к расчету примеров с четырехзначными числами. В уме решают примеры с двузначными числами. Знают таблицу умножения на скорость.

Через 3 года занятий (к 8 годам): Ребенок в уме проводит вычисления с четырехзначными числами — сложение, вычитание, умножение, деление, извлечение квадратного корня и выведение процента.

Результаты детей 6-7 лет:

Через 2 месяца занятий: Дети складывают и вычитают на абакусе двузначные числа, а в уме считают легкие примеры с двузначными числами и одинаковыми цифрами, например 11+66-55+77 и т. д.

Через 4 месяца занятий: Дети складывают и вычитают на абакусе двузначные числа, используя несложные формулы, а в уме они решают легкие примеры, такие как 11+66-55+77, 54+45-31-15, и т.д.

Через 1 год занятий: Дети складывают и вычитают на абакусе двузначные и трехзначные числа, переходят к расчету примеров с четырехзначными числами. В уме решают примеры с двузначными числами. Знают таблицу умножения на скорость.

Через 2,5 года занятий: Ребенок в уме проводит вычисления с четырехзначными числами — сложение, вычитание, умножение, деление, извлечение квадратного корня и выведение процента.

Результаты детей старше 8 лет

Через 2 месяца занятий: Дети складывают и вычитают на абакусе двузначные числа, используя несложные формулы, а в уме решают легкие примеры, такие как 11+66-55+77, 54+45-31-15, и т.д.

Через 9 месяцев занятий: Дети складывают и вычитают на абакусе двузначные и трехзначные числа, переходят к расчету примеров с четырехзначными числами.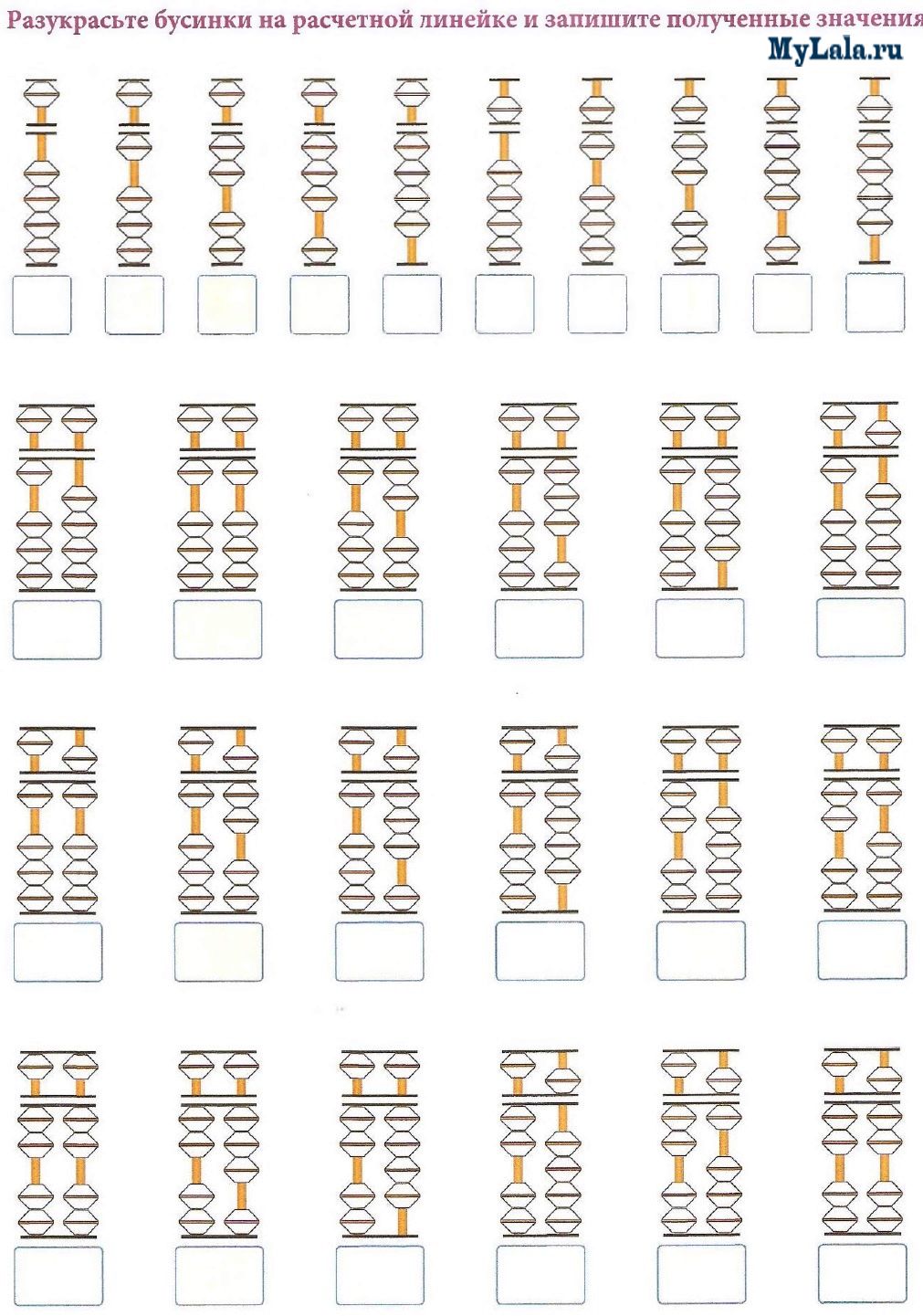 В уме решают примеры с двузначными числами. Знают таблицу умножения на скорость.

Через 2,5 года занятий: Ребенок в уме проводит вычисления с четырехзначными числами — сложение, вычитание, умножение, деление, извлечение квадратного корня и выведение процента.

Организационные моменты

Расписание: занятия проводятся 1 раз в неделю по 2 академических часа.

Общая продолжительность курса: 2,5-3 года.

Запишитесь на пробное занятие по телефону +7 495 724 19 04 или заполнив форму на этом сайте.

Ментальная арифметика для детей. Развитие ребенка. Развитие памяти, логики, внимания. Развивающие занятия для детей

Подробная информация о курсе

Ментальная арифметика — это методика, по которой дети научатся быстро совершать в уме сложные арифметические вычисления (от скоростного сложения 100+ чисел до операций с десятичными числами и извлечения корней). 

Кому можно заниматься ментальной арифметикой? 

Ментальная арифметика показана всем детям от 4 лет, которые:

  • Умеют считать от 1 до 10.
  • Умеют соотносить изображение цифры с ее названием.
  • Умеют писать цифры.
  • Имеют развитую мелкую моторику.

Как работает ментальная арифметика? 

Счет на абакусе
Дети учатся считать на абакусе — древних китайских ментальных счетах.

Представление
Дети решают примеры, представляя абакус мысленно. Ребенок учится концентрироваться до тех пор, пока не решит пример.

Автоматизм
Действия доводятся до автоматизма и примеры усложняются. С увеличением сложности, количество объектов возрастает и развивается распределение внимания.

Формулы
Запоминание большого количества формул. У детей развивается краткосрочная память при решении примеров. Долгосрочная — при запоминании формул Фотографическая — при работе с флеш-картами.

Занятия по ментальной арифметике дают детям многое: 

Развивается мышление, творческий потенциал, воображение
Ваш ребенок начинает думать на несколько шагов вперед и применять знания для решения конкретных задач.

Развиваются навыки выполнения сложных расчетов в уме


Занятия по математике выходят на новый уровень

Повышается концентрация внимания ребенка
Ваш ребенок успешнее справляется с заданиями в школе и дома

Улучшается поведение, появляется уверенность в себе
Ваш ребенок сможет смело общаться со сверстниками и взрослыми, находить друзей

Программа полного курса включает в себя 6 уровней обучения:

Уровень S 
Знакомство с абакусом, его составляющими, правилами работы с ним

Длительность: 3 месяца

Результат: дети узнают как правильно складывать и вычитать на абакусе. Активно развивается навык мелкой моторики: почерк, манипуляция с мелкими предметами. Первые заметные улучшения успеваемости в школе.

Уровень M
Закрепление навыков, изучение формул счета

Длительность: 3 месяца

Результат: ребенок начинает считать по формулам.

Ощутимо улучшается память и концентрация внимания. Заметно лучше запоминаются стихотворения, и виден прогресс в артикуляции.

Уровень А
Доведение техник сложения и вычитания до автоматизма

Длительность: 5-6 месяцев

Результат: дети могут посчитать любые примеры на сложение и вычитание за считанные секунды. Феноменально развиваются воображение, представление и фотографическая память.

Уровень R
Умножение на абакусе

Длительность: 3 месяца

Результат: молниеносный ментальный счет, доскональное знание и оперирование таблицей умножения, увеличение скорости счета. Значительно вырастает способность к аналитической деятельности, самостоятельность и заметно повышается самооценка.

Уровень T
Техника деления на абакусе

Длительность: 3 месяца

Результат: ребенок делит на абакусе, используя уже изученные формулы.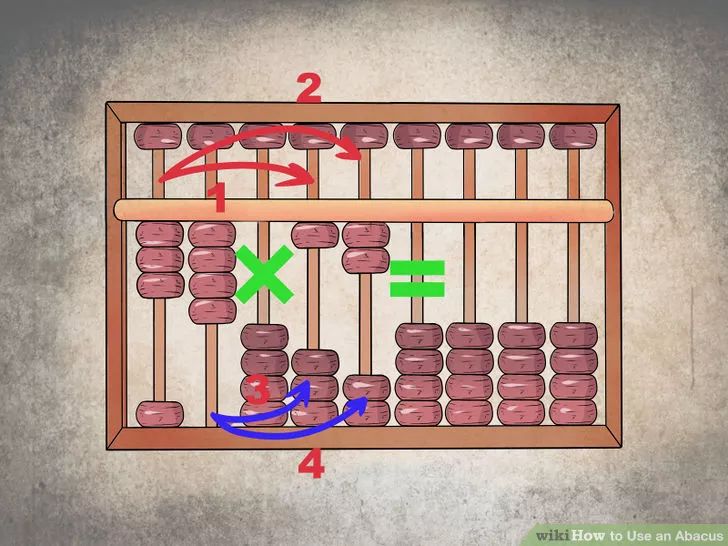 На этом этапе ребенок тратит минимальное время на решение любых арифметических задач в школе. Многие дети занимают призовые места на олимпиадах.

Уровень Y
Техника счета отрицательных и десятичных чисел, квадратных и кубических корней на абакусе

Длительность: 3 месяца

Результат:  ребенок не только с легкостью подходит к решению любых задач как в школе, так и в жизни. Активно выражено стремление к лидерству, умение аргументированно отстаивать свою точку зрения, улучшается успеваемость по большей части предметов в школе.

Занятия на курсе по ментальной арифметике ведут сертифицированные преподаватели, в группах до 6 детей.
Для достижения результатов ребенку необходимо ежедневное выполнение домашних заданий (15 минут в день).

Дошкольники занимаются 2 раза в неделю, продолжительность каждого занятия — 60 минут. 
Школьники занимаются 1 раз в неделю, продолжительность занятия — 105 минут.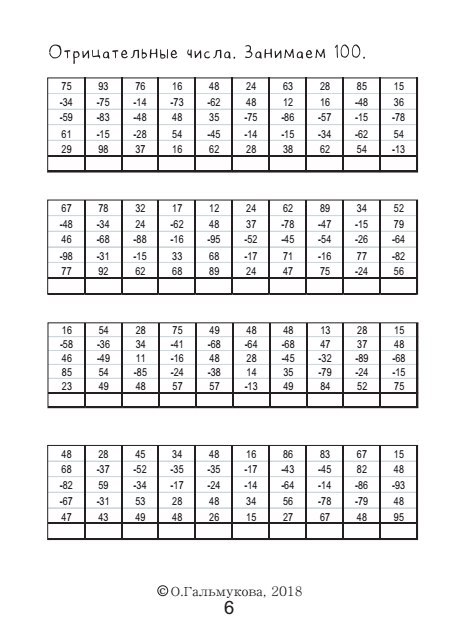  


Дополнительно приобретается комплект учебных материалов. 



Что такое ментальная арифметика и как ей научиться

Фото: Chris Liverani / Unsplash

Как устный счет помогает решать творческие задачи и готовит ребенка к будущему, рассказывает методист «Фоксфорда» Анастасия Кузнецова

Об эксперте: Анастасия Кузнецова, методист онлайн-школы «Фоксфорд», автор и преподаватель курсов повышения квалификации по ментальной арифметике.

Что такое ментальная арифметика

Попробуйте за несколько секунд решить пример без черновика и калькулятора:

Дети решают такие задачи в уме с помощью ментальной арифметики. Это система развития интеллекта, построенная на обучении устному счету.

Современные родители часто рассказывают о неразвитом воображении и фантазии у ребенка. Дело в том, что мы тренируем левое полушарие мозга ребенка — оно отвечает за логику и математические способности, — но очень мало развиваем правое. Правое полушарие мозга распознает сложные визуальные и звуковые образы. Отвечает за концентрацию внимания и воображение. От гармоничного развития двух полушарий мозга ребенка зависят его когнитивные способности [1].

Ментальная арифметика — это способ развития детского интеллекта с помощью быстрого счета в уме. Сначала ребенок учится считать на счетах-абакус и тренирует мелкую моторику рук. Затем счеты убирают, ребенок представляет их в голове — считает ментально. Развивает воображение и креативность.

Ментальная арифметика помогает комплексно развивать интеллектуальные способности. Моментальный устный счет — приятное дополнение.

Овладев ментальной арифметикой, ребенок намного легче справляется с любой интеллектуальной и творческой работой. Он умеет быстро решать задачи и применять к ним нестандартный подход.

История возникновения ментальной арифметики

Ментальную арифметику придумали около 5 тыс. лет назад. Методикой пользовались в Древней Греции, Индии и Риме, чтобы научить детей считать. В ее основе — умение вычислять на древних счетах-абакус.

Со временем счеты доработали до калькулятора, в 1993 году сформулировали понятие «ментальной арифметики». Сегодня ментальную арифметику используют в 50 странах мира. В Японии и Китае она стала частью школьной программы.

Счеты-абакус — главный инструмент ментальной арифметики. На занятиях ученики работают с доской и счетами, а после — считают только в уме. В Японии такие счеты называют соробан (Фото: Unsplash)

Польза ментальной арифметики

Умение быстро вычислять в уме — не конечная цель. В момент отказа от работы с реальными счетами-абакус правое полушарие мозга начинает работать активнее. В это же время дети развивают логическое мышление и счет, за которые отвечает левое полушарие.

Усиленная работа обоих полушарий мозга становится привычкой и помогает ребенку креативнее решать жизненные задачи. Концентрироваться, смотреть на проблему шире и строить логические цепочки для ее решения. Еще один плюс — развитие сразу нескольких видов памяти: долговременной, кратковременной и фотографической.

Что ученые думают о ментальной арифметике

Американские исследователи проверяли влияние ментальной арифметики на интеллектуальные способности учеников первых и вторых классов в течение года [2]. Результаты получились неоднозначными — первоклассники не справлялись с устным счетом, ребята из второго класса учились лучше, но ученые не выявили заметного улучшения когнитивных способностей.

В 2016 году психолог Дэвид Барнер группой ученых провел подобное исследование в Индии, но за детьми наблюдали уже в течение трех лет [3]. Ментальная арифметика помогла некоторым школьникам лучше учиться, но результат может зависеть и от способностей конкретного ученика. В большинстве других исследований тоже проверяли навыки арифметики. Достаточного количества данных о том, как ментальная арифметика влияет на когнитивные способности, пока нет, поэтому выводы делать рано.

Когда и где учиться ментальной арифметике

Самый подходящий возраст для обучения — от 4 до 12-14 лет. В это время мозг развивается интенсивнее, чем в другие периоды взросления. После 12-14 лет способность мозга приобретать и использовать сложные навыки в таком количестве и темпе снижается.

Сейчас набирают популярность занятия ментальной арифметикой с пожилыми людьми. Такая тренировка мозга — отличный метод профилактики болезней, связанных с памятью и концентрацией внимания.

Самостоятельное обучение может стать непростой задачей. Учеба требует усидчивости, внимательности и разнообразные форматы занятий. Чтобы правильно обучить ребенка ментальной арифметике, лучше обратиться к квалифицированному педагогу.

Как выбрать школу или курс ментальной арифметики

Чтобы выбрать подходящую школу ментальной арифметики для ребенка, проверьте:

  1. Сколько детей в группе. Чем младше дети, тем меньше должна быть группа. Рекомендуемый размер группы для дошкольников — до восьми человек, для начальной школы — до десяти человек.
  2. Какая квалификация у преподавателя. Преподавателю необходимы профильные навыки. Он может их получить в центрах ментальной арифметики. Узнайте об образовании педагога и посмотрите его сертификаты. Международный сертификат по ментальной арифметике — дополнительный плюс.
  3. Дают ли учебные материалы. Одно из важнейших условий обучения — возможность наблюдать за каждым действием педагога. Так вы сможете проверить учебные материалы и качество образования. Хорошим решением может стать онлайн-платформа.
  4. Есть ли домашние задания. Ментальная арифметика предполагает регулярное закрепление полученных знаний, поэтому важно обратить внимание на качество и формат домашних заданий.
  5. Есть ли пробное занятие. Для ребенка это безопасная возможность попробовать ментальную арифметику, для вас — проверить качество школы или курса.

Что такое ментальная арифметика | Детский клуб «Академиум»

Детский клуб «Академиум».

Методист Ирина Астахова

Что такое ментальная арифметика? Ментальная арифметика — это древняя система счета, проверенная тысячелетиями на Востоке, когда арифметические действия производятся в уме с помощью воображения специальных восточных счетов — абакуса (или соробана). Эта техника счета применяется более 2 тысяч лет в Китае и Японии.

Что же дает курс ментальной арифметики детям? Благодаря одновременной работе правой и левой руки на абакусе во время решения примеров у детей в возрасте от 4 до 12 (иногда до 16) лет активизируются оба полушария мозга, образуются новые нейронные связи, происходит интенсивное развитие головного мозга. Навыки и знания, полученные в этот период, отлично усваиваются и закрепляются на долгие годы вперед. Именно поэтому они могут оказать значительное влияние на успешное будущее вашего ребенка. Многие международные научные исследования подтверждают пользу ментальной арифметики:

  • ►Lynn R. , Irwing P. (2008) Effect of Abakus trainig on the intelligence of Sudanese children.
  • ►Min-Sheng Chen, Chang-Tzu Wang. (2011) Effect of mental abacus training on working memory for children.
  • ►Bhaskaran M., Sengottaiyan A., (2006). Evaluation of Memory in Abacus Learners. Indian J Physiol Pharmacol.
Сначала дети учатся считать с помощью косточек на абакусе, постепенно переходя на счет в уме (ментальный счет), представляя в воображении арифметические действия на абакусе. В общем итоге, во время занятий ментальной арифметикой дети развивают:
  • ►воображение (представляя абакус)
  • ►логику (применяя формулы)
  • ►память (во время расчетов итоги и подитоги держатся в уме)
  • ►внимание (постоянно тренируется во время решения примеров и выполнения упражнений)
  • ►восприятие информации (при решении примеров на слух)
Как результат, дети становятся более уверенными в себе и своих силах, проявляют успехи и в творчестве, и при обучении иностранным языкам. Успеху способствует и улучшение усваиваемости школьного материала — оценки и баллы становятся выше, что подтверждается многолетней практикой ментальной арифметики в России и в Казахстане.

Откройте маленького гения в своем ребенке! Посетите пробный урок в детском клубе «Академиум» бесплатно! График занятий и цены, а также предварительная запись на занятия по телефону (351) 77-77-527.

Реши примеры worksheet

Advanced search

Content:

Language: AfarAbkhazAvestanAfrikaansAkanAmharicAragoneseArabicAssameseAsturianuAvaricAymaraAzerbaijaniBashkirBelarusianBulgarianBihariBislamaBambaraBengali, BanglaTibetan Standard, Tibetan, CentralBretonBosnianCatalanChechenChamorroCorsicanCreeCzechOld Church Slavonic, Church Slavonic,Old BulgarianChuvashWelshDanishGermanDivehi, Dhivehi, MaldivianDzongkhaEweGreek (modern)EnglishEsperantoSpanishEstonianBasquePersian (Farsi)Fula, Fulah, Pulaar, PularFinnishFijianFaroeseFrenchWestern FrisianIrishScottish Gaelic, GaelicGalicianGuaraníGujaratiManxHausaHebrew (modern)HindiHiri MotuCroatianHaitian, Haitian CreoleHungarianArmenianHereroInterlinguaIndonesianInterlingueIgboNuosuInupiaqIdoIcelandicItalianInuktitutJapaneseJavaneseGeorgianKongoKikuyu, GikuyuKwanyama, KuanyamaKazakhKalaallisut, GreenlandicKhmerKannadaKoreanKanuriKashmiriKurdishKomiCornishKyrgyzLatinLuxembourgish, LetzeburgeschGandaLimburgish, Limburgan, LimburgerLingalaLaoLithuanianLuba-KatangaLatvianMalagasyMarshalleseMāoriMacedonianMalayalamMongolianMarathi (Marāṭhī)MalayMalteseBurmeseNauruanNorwegian BokmålNorthern NdebeleNepaliNdongaDutchNorwegian NynorskNorwegianSouthern NdebeleNavajo, NavahoChichewa, Chewa, NyanjaOccitanOjibwe, OjibwaOromoOriyaOssetian, OsseticEastern Punjabi, Eastern PanjabiPāliPolishPashto, PushtoPortugueseQuechuaRomanshKirundiRomanianRussianKinyarwandaSanskrit (Saṁskṛta)SardinianSindhiNorthern SamiSangoSinhalese, SinhalaSlovakSloveneSamoanShonaSomaliAlbanianSerbianSwatiSouthern SothoSundaneseSwedishSwahiliTamilTeluguTajikThaiTigrinyaTurkmenTagalogTswanaTonga (Tonga Islands)TurkishTsongaTatarTwiTahitianUyghurUkrainianUrduUzbekValencianVendaVietnameseVolapükWalloonWolofXhosaYiddishYorubaZhuang, ChuangChineseZulu    Subject:   

Grade/level:    Age: 3456789101112131415161718+

Search: All worksheetsOnly my followed usersOnly my favourite worksheetsOnly my own worksheets

Ментальный калькулятор

Математика – самый нелюбимый предмет в школе для большинства детей. Сложные вычисления на бумаге и ворох функций, интегралов и чисел отталкивают от себя непоседливых школьников, особенно когда они понимают, что трехстраничные решения примеров никогда не пригодятся им в жизни. А что, если большие числа можно научиться вычислять в уме? Центр ментальной арифметики «Smarty Kids» обучает детей именно этому, просто играя с ними.

Полный абакус

Ментальная арифметика – это счёт в уме. То есть даже самые сложные примеры ребенок, владеющий этим приемом, сможет решить без помощи ручки и бумаги. Суть метода заключается в визуализации чисел. Добиться такого эффекта помогает хитроумный на вид, а на самом деле очень простой в использовании счетный инструмент – абакус. Внешне он напоминает счёты, да и действует практически также.

— Конструкция абакуса очень похожа на нашу руку. Именно поэтому детям просто визуализировать последовательность косточек, чтобы сделать вычисления. Сначала мы считаем единицы – в разных последовательностях, на разных скоростях, а уже потом переходим к десяткам, сотням и тысячам, — рассказала руководитель центра ментальной арифметики «Smarty Kids» Татьяна Ланцева.

Фото: detstvodetstvo.ru

Самый оптимальный возраст для изучения ментальной арифметики – 6-12 лет. Именно в этот промежуток времени ребенку легче всего перестроиться под счет в уме. Но есть в центре «Smarty Kids» и группы для малышей от 4 лет и для более взрослых детей.

— Абакус – это не только большой предмет, на котором надо перемещать косточки. Есть еще и маленький. Ребятишки воспринимают его, как массажер, катают по нему ручками. Из-за этого на ладошках активизируются все активные зоны. То есть по факту, ребенок еще ничего не знает про абакус, но ему уже нравится, — рассказала Татьяна Владимировна.

«Бешеный» счет

Занимаясь ментальной арифметикой, ребенок может дойти до уровня «бешеного счета». Именно таких результатов добился учитель Татьяны Ланцевой, чемпион мира по ментальной арифметике Девид Ляо. Сегодня он уже соревнуется в скорости вычислений с компьютером.

— «Бешеный» счет нужен не для того, чтобы быстро-быстро считать.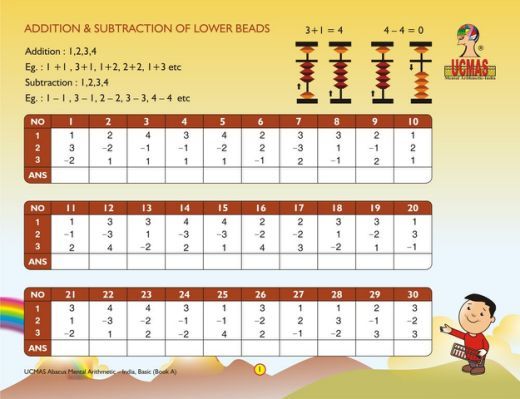 Он развивает мозг, активизируются все психические процессы. Мы работаем не для того, чтобы ребенок моментально начал быстро считать. Мы развиваем воображение, память, концентрацию. Бывали случаи, что даже самые гиперактивные дети, которые вообще не могут спокойно сидеть на месте, начинали концентрироваться, находились внутренние резервы для того, чтобы спокойно заниматься одним делом продолжительное время, — добавила руководитель центра.

Обучение проводится в игровой форме. Дети не сидят за партами – они играют, читают, занимаются зарядкой и при всем этом считают.

— Для ребенка это не обучение – это игра, развлечение. Дети находятся среди сверстников, и все они увлечены одним делом. Такой метод работы очень продуктивен, ведь ребятам незачем отлынивать от занятий, потому что они воспринимают учебный процесс, как что-то увлекательное и интересное, — рассказала Татьяна Ланцева.

Новый друг Смартик

Во время занятий дети находят себе не только друзей-сверстников.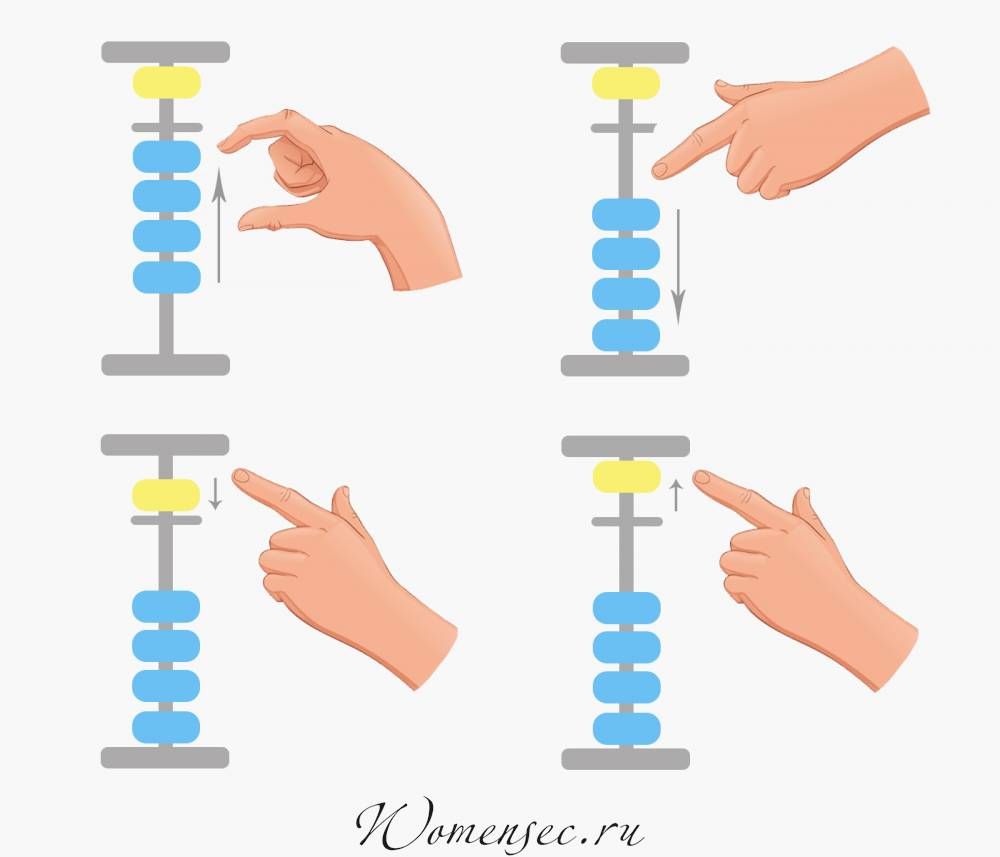 У них появляется и еще один приятель Смартик – мальчик-проводник в мир ментальной арифметики. С помощью специального приложения, которое можно установить на мобильный телефон, Смартик «оживает». Проще говоря, вместо рисунка-помощника в учебнике, дети видят мультяшного персонажа, который помогает понять предмет и дает полезные советы.

— В учебнике есть продуманная и увлекательная геймификация. Она учтена на протяжении всего учебного процесса, — сообщила педагог.

Школьная программа отдыхает

К сожалению, в школьной программе в России занятия ментальной арифметикой просто не предусмотрены. Происходит это даже несмотря на то, что множество продвинутых стран – Япония, Китай, Корея, Индия и другие, давно внедрили этот предмет в учебные заведения.

Интересно, что цена занятий и количество академических часов рассчитывается в центре ментальной арифметики «Smarty Kids» индивидуально для каждого ребенка в зависимости от его особенностей.

— Каждый ребенок индивидуален. То, что один поймет всего за одно занятие, у другого займет три. Поэтому, чтобы сориентировать родителей по времени обучения и его стоимости, нам необходимо пообщаться с ребенком, найти с ним точки соприкосновения, понять, что ему интересно. Мы применяем только индивидуальный подход, — рассказала Ланцева.

Ученики центра регулярно принимают участие в олимпиадах всероссийского уровня. Они входят в десятку лучших по всей стране.

Центр ментальной арифметики «Smarty Kids» вы найдете по адресу: г. Чита, ул. Кастринская, 6, ул. Белорусская, 4, КСК СРЦ «Страна чудес», ул. Красной Звезды, 51А, ДК «Железнодорожников». Получить консультацию специалистов и задать интересующие вас вопросы можно по телефону: 8-914-463-54-44.

Smarty Kids Чита, ул. Кастринская, 6, ул. Белорусская, 4, КСК СРЦ «Страна чудес», ул. Красной Звезды, 51А, ДК «Железнодорожников»8-914-463-54-44

На правах рекламы

Методика ментальной арифметики

Дошкольники и школьники: 1 уровень «Просто»

Сложение и вычитание на уровне «Просто» (9 недель, 80 страниц)

Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.)

1-я неделя. Знакомство с абакусом. Сложение и вычитание примеров с числами от 0 до 4 на абакусе и ментально. Флеш-карты. Состав числа 1-4. Развитие обеих рук. Логика. Развития внимания. Нейрогимнастика. 8 листов.

2-я неделя. Сложение и вычитание примеров с числами 0-7 на абакусе и ментально. Флеш-карты. Состав числа 5-7. Развитие обеих рук. Логика. Развитие внимания. Нейрогимнастика. 8 листов.

3-я неделя. Сложение и вычитание примеров с числами 0-9 на абакусе и ментально. Флеш-карты. Состав числа 8-9. Развитие обеих рук. Логика. Развитие внимания. Нейрогимнастика. 8 листов.

4-я неделя. Знакомство с сотней. Сложение и вычитание примеров с круглыми и парными двузначными числами на абакусе и ментально. Флеш-карты. Состав чисел второго десятка. Развитие обеих рук. Логика. Развитие внимания. Нейрогимнастика. 8 листов.

5-я неделя. Сложение и вычитание примеров с двузначными числами на абакусе и ментально. Флеш-карты. Состав числа в сотне. Понятие четных и нечетных чисел. Повторение состава числа 5 и 10 (подготовка к формулам). Развитие обеих рук. Логика. Развитие внимания. Нейрогимнастика. 8 листов.

6-я неделя. Сложение и вычитание примеров с чередованием двузначных и однозначных чисел на абакусе и ментально. Двузначные флеш-карты. Счёт в сотне. Числа соседи. Повторение состава числа 10 (подготовка к формулам). Развитие обеих рук. Логика. Развитие внимания и пространственного мышления. Нейрогимнастика. 8 листов.

7-я неделя. Сложение и вычитание примеров с трёхзначными числами на абакусе. Трёхзначные флеш-карты. Счёт в сотне, состав числа сотни, состав трёхзначного числа. Числа соседи. Последовательность чисел в сотне. Понятие тысячи. Работа с монетной системой. Развитие обеих рук. Логика. Развитие внимания и пространственного мышления. Нейрогимнастика. 8 листов.

8-я неделя. Закрепление. Сложение и вычитание примеров с трёхзначными числами на абакусе и ментально. Трёхзначные флеш-карты. Счёт в сотне, состав числа сотни, состав трёхзначного числа. Числа соседи. Последовательность чисел в сотне. Понятие тысячи. Работа с монетной системой. Развитие обеих рук. Логика. Развитие внимания и пространственного мышления. Нейрогимнастика. 8 листов.

9-я неделя. Итоговое занятие по первому уровню. Сложение и вычитание примеров с одно-, дву- и трёхзначными числами на абакусе и ментально. Замер скорости и правильности решения примеров. Двузначные и трёхзначные флеш-карты. Счёт в сотне, состав числа второго десятка, сотни. Работа с монетной системой. Развитие обеих рук. Логика. Развитие внимания и пространственного мышления. Нейрогимнастика. 8 листов.

Дошкольники и школьники: 2 уровень «Помощь брата»

Сложение и вычитание на уровне «Помощь брата» (9 недель, 80 страниц)

Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.)

10-я неделя. Состав числа 5, сложение и вычитание. Формулы +4=+5-3, -4=-5+3. Однозначные, двузначные числа, трехзначные числа. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов.

11-я неделя. Состав числа 5, сложение и вычитание. Формулы +4=+5-3, -4=-5+3. Однозначные, двузначные числа, трехзначные числа. Счёт сотен. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов.

12-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3. Формулы +3=+5-2. Однозначные, двузначные. Трехзначные без новых формул. Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов.

13-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3. Формулы +3=+5-2, -3=-5+2. Однозначные, двузначные, трехзначные. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов.

14-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3, +3=+5-2, -3=-5+2. Формулы: +2=+5-3; Однозначные, двузначные; Трехзначные без новых формул. Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов.

15-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3, +3=+5-2, -3=-5+2. Формулы: +2=+5-3; -2=-5+3; Однозначные, двузначные, трехзначные. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов.

16-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3, +3=+5-2, -3=-5+2, +2=+5-3; -2=-5+3; Формулы: +1=+5-4. Однозначные, двузначные; Трехзначные без новых формул. Понятие умножение. Умножение через сложение. Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов.

17-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3, +3=+5-2, -3=-5+2, +2=+5-3, -2=-5+3, +1=+5-4; Формулы: -1=-5+4. Однозначные, двузначные; Трехзначные без новых формул. Понятие умножение. Умножение через сложение. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов.

18-я неделя. Закрепление формул: +4=+5-3, -4=-5+3, +3=+5-2, -3=-5+2, +2=+5-3; -2=-5+3; Формулы: +1=+5-4, -1=-5+4; Однозначные, двузначные, трехзначные. Умножение через сложение. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов.

19-я неделя. Итоговое занятие, получение 2 уровня. Замер скорости и правильности работы с вычислениями на абакусе с формулами «Помощь брата».Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов.

Дошкольники и школьники: 3 уровень «Помощь друга»

Сложение и вычитание на уровне «Помощь друга» (13 недель, 105 страниц)

Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.)

20-я неделя. Состав числа 10. Сложение и вычитание с формулой «помощь друга» +9 и -9. Знакомство с переходом через 50. . Закрепление формул «Помощь брата». Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов.

21-я неделя. Сложение и вычитание с формулой «помощь друга» +8 и -8. Закрепление формул «Помощь брата», «Помощь друга +-9», перехода через 50. Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов.

22-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; Новые формулы: +7=+10-3; -7=-10+3; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов.

23-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; Новые формулы: +6=+10-4; -6=-10+4; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов.

24-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; +6=+10-4; -6=-10+4; Новые формулы: +5=+10-5; -5=-10+5; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов.

25-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; +6=+10-4; -6=-10+4; +5=+10-5; -5=-10+5; Новые формулы: +4=+10-6; -4=-10+6; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов.

26-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; +6=+10-4; -6=-10+4; +5=+10-5; -5=-10+5; +4=+10-6; -4=-10+6; Новые формулы: +3=+10-7; -3=-10+7; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов.

27-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; +6=+10-4; -6=-10+4; +5=+10-5; -5=-10+5; +4=+10-6; -4=-10+6; +3=+10-7; -3=-10+7; Новые формулы: +2=+10-8; -2=-10+8; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов.

28-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; +6=+10-4; -6=-10+4; +5=+10-5; -5=-10+5; +4=+10-6; -4=-10+6; +3=+10-7; -3=-10+7; +2=+10-8; -2=-10+8; Новые формулы: +1=+10-9; -1=-10+9; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов.

29-я неделя. Интенсив на переход через 50 на абакусе. Повторение всех формул «Помощь брата и друга». Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Каллиграфия чисел. 8 листов.

30-я неделя. Переход через 100 на абакусе. Повторение всех формул «Помощь брата и друга». Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.

31-я неделя. Закрепление формул друга и переходов через 50, 100. Повторение всех формул «Помощь брата и друга». Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Каллиграфия чисел. 8 листов.

32-я неделя. Итоговое занятие по третьему уровню. Замеры на время и правильность решения примеров со всеми формулами «помощь брата и друга» и переходами через 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.
ями на абакусе с формулами «Помощь брата».Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов.

Дошкольники и школьники: 4 уровень «Микс формулы»

Сложение и вычитание на уровне «Формулы Микс» (5 недель, 40 страниц)

Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.)

33-я неделя. Формула «Микс»: +6=+10-5+1 и -6=-10+5-1. Закрепление формул «Помощь брата и друга» и переходов через 50, 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Каллиграфия чисел. 8 листов.

34-я неделя. Формула «Микс»: +7=+10-5+2 и -7=-10+5-2. Закрепление формул «Помощь брата и друга» и переходов через 50, 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.

35-я неделя. Формула «Микс»: +8=+10-5+3 и -8=-10+5-3. Закрепление формул «Помощь брата и друга» и переходов через 50, 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.

36-я неделя. Формула «Микс»: +9=+10-5+4 и -9=-10+5-4. Закрепление формул «Помощь брата и друга» и переходов через 50, 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.

37-я неделя. Итоговое занятие по миксам формул. Замеры на время и правильность решения примеров со всеми формулами «помощь брата, друга и микс» и переходами через 50 и 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.

Дошкольники и школьники: 5 уровень «Анзан, сложение и вычитание без ограничений»

Сложение и вычитание на уровне «Анзан» (4 недели, 48 страниц)

Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.)

38-я неделя. Счёт АНЗАН — вычисления без ограничений. Замеры на время и правильность решения примеров со всеми формулами «помощь брата, друга и микс» и переходами через 50 и 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.

39-я неделя. Счёт АНЗАН. Закрепление. Головоломки и игры на решение примеров со всеми формулами «помощь брата, друга и микс» и переходами через 50 и 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. 8 листов.

40-я неделя. Итоговое занятие по пятому уровню. Замеры на время и правильность решения примеров без ограничений (анзан). Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. 8 листов.

41-я неделя. (Запасная) Счёт АНЗАН. Решебник. Усложнённый счёт анзан на абакусе. Игровые упражнения и упражнения на повторение тем года. 8 листов.

Дошкольники и школьники: 6 уровень «Умножение»

Умножение (16 недель, 64 страницы)

Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.)

6 уровень. Умножение ч.1. 11-й месяц.
Умножение двузначного числа на однозначное (x2, 3, 4, 5). Рабочие схемы и правила. Сложение/вычитание анзан. (4 стр.)
Умножение двузначного числа на однозначное (x6, 7, 8, 9). Сложение/вычитание анзан. (4 стр.)
Умножение трёхзначного числа на однозначное (x 2, 3, 4, 5, 6). Рабочие схемы и правила. Сложение/вычитание анзан. (4 стр.)
Умножение трёхзначного числа на однозначное (x7, 8, 9). Сложение/вычитание анзан. (4 стр.)

6 уровень. Умножение ч.2. 12-й месяц.
Умножение двузначного числа на двузначное. Рабочие схемы и правила. Сложение/вычитание анзан. (4 стр.)
Умножение трехзначного числа на двузначное. Рабочие схемы и правила. Сложение/вычитание анзан. (4 стр.)
Умножение трехзначного числа на трехзначное и повторение предыдущих тем. (8 стр.)

6 уровень. Умножение ч.3. 13-й месяц.
Умножение трехзначного числа на трехзначное и повторение предыдущих тем. (4 стр.)
Практикум умножения и сложения/вычитания анзан. (12 стр.)

6 уровень. Умножение ч.4. 14-й месяц.
Практикум умножения и сложения/вычитания анзан. (5 стр.)
Умножение четырёхзначного числа на трехзначное и повторение предыдущих тем. (4 стр.)
Практикум умножения всех предыдущих тем и сложения/вычитания анзан. (7 стр.)

Дошкольники и школьники: 7 уровень «Деление»

Деление (12 недель, 48 страниц)

Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.)

7 уровень. Деление ч.1. 15-й месяц.
Деление двузначного числа на однозначное (/2, 3, 4, 5). Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (4 стр.)
Деление двузначного числа на однозначное (/2, 3, 4, 5, 6, 7, 8, 9). Умножение и сложение/вычитание анзан. (4 стр.)
Деление трёхзначного числа на однозначное (/2, 3, 4, 5). Умножение и сложение/вычитание анзан. (4 стр.)
Деление трёхзначного числа на однозначное (/6, 7, 8, 9). Умножение и сложение/вычитание анзан. (4 стр.)

7 уровень. Деление ч.2. 16-й месяц.
Деление четырёхзначного числа на однозначное. Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (4 стр.)
Деление трехзначного числа на двузначное (/2, 3, 4, 5). Умножение и сложение/вычитание анзан. (4 стр.)
Деление трехзначного числа на двузначное (/2, 3, 4, 5, 6, 7, 8, 9). Умножение и сложение/вычитание анзан. (4 стр.)
Деление четырехзначного числа на двузначное (/2, 3, 4, 5). Умножение и сложение/вычитание анзан. (4 стр.)

7 уровень. Деление ч.3. 17-й месяц.
Деление четырехзначного числа на двузначное. (/2, 3, 4, 5, 6, 7, 8, 9). Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (4 стр.)
Практикум умножения, деления и сложения/вычитания анзан. (12 стр.)

Школьники: 8 уровень «Дроби»

Дроби (4 недели, 16 страницы)

Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.)

8 уровень. Дроби. 18-й месяц.
Понятие и работа с десятичными дробями. Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (16 стр.)

Школьники: 9 уровень «Отрицательные числа»

Отрицательные числа (4 недели, 16 страниц)

Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.)

9 уровень. Отрицательные числа. 19 месяц.
Понятие и работа с отрицательными числами. Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (16 стр.)

Школьники: 10 уровень «Квадратные корни»

Квадратные корни (4 недели, 16 страниц)

Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.)

10 уровень. Квадратные корни. 20 месяц.
Понятие и работа с квадратными корнями. Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (16 стр.)

Дошкольники: 8-10 уровень решебник «Умножение и деление»

Решебник  «Умножение и деление» (12 недель, 30 страниц)

Решебник.
Для детей дошкольного возраста на умножение и деление сложение/вычитания анзан (30 стр.).

Краткосрочный интенсив «Простое сложение и вычитание»

Краткосрочный интенсив «Простое сложение и вычитание»
(4 недели, 4 темы, 21 страница)

Тетрадь дополнена пояснительными записками учителю.

  • Знакомство с абакусом.
  • Простое сложение и вычитание чисел от 1 до 99.
  • Использование монетной системы, флеш-карт, подробное описание работы с абакусом для начинающих.
  • Классическая и ментальная арифметика.

Работу с краткосрочным интенсивом можно идеально дополнять работой с онлайн платформой.

Экспресс курс «Умножение»

Экспресс курс «Умножение» (20 страниц)

Тетрадь дополнена пояснительными записками учителю.

  • Умножение двузначного числа на однозначное. Рабочие схемы и правила. Сложение/вычитание анзан.
  • Умножение трёхзначного числа на однозначное. Рабочие схемы и правила. Сложение/вычитание анзан.
  • Умножение двузначного числа на двузначное. Рабочие схемы и правила. Сложение/вычитание анзан.
  • Умножение трехзначного числа на двузначное. Рабочие схемы и правила. Сложение/вычитание анзан.

Работу с краткосрочным интенсивом можно идеально дополнять работой с онлайн платформой.

Экспресс курс «Деление»

Экспресс курс «Деление» (20 страниц)

Тетрадь дополнена пояснительными записками учителю.

  • Деление двузначного числа на однозначное. Рабочие схемы и правила. Сложение/вычитание анзан.
  • Деление трёхзначного числа на однозначное. Сложение/вычитание анзан.
  • Деление четырёхзначного числа на однозначное. Сложение/вычитание анзан.
  • Деление трехзначного числа на двузначное. Сложение/вычитание анзан.
  • Деление четырехзначного числа на двузначное. Сложение/вычитание анзан.

Работу с краткосрочным интенсивом можно идеально дополнять работой с онлайн платформой.

Abacus — Cuemath

Знаете ли вы, что Cranmer Abacus специально разработан для работы слепых людей?

Счеты помогают нам понять математические концепции, развивая чувство числа, чего не всегда можно достичь с помощью калькулятора.

В этом мини-уроке мы узнаем о счетах — как пользоваться, калькулятором и изучим счеты, когда мы изучим концепцию счеты.

План урока

Что такое счеты?

Счеты — это простое счетное устройство, состоящее из бусинок, размещенных в стержнях из проволоки, заключенных в деревянную раму.

Расчеты можно производить, сдвигая валики по стержням.

Части Abacus

Различные части абака:

  • Внешняя граница счет называется рамкой.
  • Счеты, которые мы используем в настоящее время, имеют 17 стержней, и на каждом стержне 5 бусинок.
  • В счетах два деления. Горизонтальная планка, разделяющая верхнюю и нижнюю часть, называется балкой.
  • Бусинки, находящиеся в нижней части, называются нижними бусинками или земляными бусинками.
  • Бусинки, находящиеся в верхней части, называются верхними бусинами или небесными бусинками.

Как считать числа на счетах?

Счеты — это устройство, которое можно использовать для счета, сложения, вычитания, умножения и т. Д.

  • Крайний правый столбец — для своего места.
  • Следующий столбец используется для разряда десятков.
  • Третий столбец справа предназначен для разряда сотен и так далее.{\ text {rd}} \) в правом нижнем углу.

2. Считаем 8 в верхнем и нижнем ряду:

  • Используйте 1 бисеринку из верхнего ряда, что эквивалентно 5 и 3 бисеринкам из нижнего ряда.
  • Таким образом, расчет даст ответ 5 + 3 = 8.

В следующей таблице показаны различные счетные устройства, подобные счетам, используемые в разных странах:

Страна Устройство
Китай Суанпан
Япония Соробан
Россия Чоты

Как складывать и вычитать с помощью Abacus?

Как только вы научитесь использовать счет для счета, вы сможете использовать его для множества других операций.

Дополнение
Стратегия 10

Если нам нужно сложить 8 + 6, мы введем 6 и 8 в первые два столбца.

Затем перейдите от 6 к 8 так, чтобы 8 стало 10, а 6 стало 4.

Итак, теперь мы можем легко использовать 10 + 4 = 14.

Освоив эту стратегию на счетах, вы можете попробовать сделать это мысленно.

Стратегия двух пятерок

Если нам нужно сложить 6 + 8, мы введем 6 и 8 в первые два провода.Две пятерки сделают 10, а у нас останется 4 бусинки. Теперь выполнить 10 + 4 = 14 легко.

Эта стратегия работает в задачах, где два добавляемых числа больше пяти.

Добавление больших чисел

Предположим, мы должны сложить 57 + 86. Нам нужно будет представить 86 на счетах.

У первого провода справа будет 6, а у второго — 8. Начните с первого провода и прибавьте 7 к 6. В результате получится 13.

Сохраните цифру 3 и перейдите от 1 к 8, получив таким образом 9.

Теперь выполните 9 + 5, что даст 14.

Итак, фактический результат будет 143.

Вычитание

Процесс вычитания противоположен сложению.

Нам просто нужно заимствовать цифры из предыдущего столбца, а не переносить их.

Пример

Если мы хотим вычесть 672 из 945,

  • Введите 945 на счетах и ​​начните вычитание столбец за столбцом слева.
  • I Если мы вычтем 2 из 5, то получим 3 вместо единицы.
  • Используйте аналогичный метод для десятичных разрядов. Поскольку мы не можем вычесть 7 из 4, нам придется занять 1 из разряда сотен, оставив 8 в разряде сотни. Теперь у нас будет 14 в десятке. Вычитая 7 из 14, получаем 7 в разряде десятков.
  • Наконец, вместо сотни мы вычтем 6 из 9, и таким образом у нас останется 3 бусины.

Таким образом, наш окончательный ответ будет 945 — 672 = 273.

Калькулятор абак

Попробуем решить математические операции с помощью следующего калькулятора абак:

Каковы преимущества использования Abacus?

На счетах:

  • Улучшает умственные арифметические вычисления
  • Повышает концентрацию
  • Обостряет память
  • Улучшает воображение
  • Повышает уверенность
  • Повышает навыки решения проблем

  1. Abacus — это полезное обучающее оборудование для слабовидящих, а также для всех, кто хочет изучить происхождение современного калькулятора.
  2. Бусинки в верхнем стержне, имеющие значение 5, называются го-дама, а 4 бусинки в нижнем ряду, каждая из которых имеет значение 1, известны как ичи-дама.

Решенные примеры

Можете ли вы помочь Марте изобразить число 3687 на счетах?

Решение

Число 3687 можно представить на счетах следующим образом:

  • Сдвиньте 2 бисеринки вверх в нижнем ряду и 1 бисеринку вниз в верхнем ряду в крайнем правом столбце.{\ text {th}} \) столбец справа.

Лиззи застряла в проблеме при сложении двух чисел. Можете ли вы помочь ей, записав шаги, чтобы сложить 456 и 796, используя счеты?

Решение

Шаги для вычисления суммы 456 и 796:

  • Нам нужно будет представить 796 на счетах.
  • Первый провод справа будет иметь 6, второй провод 9 и третий провод 7.
  • Начните с первого провода и прибавьте 6 к 6. В результате получится 12. Сохраните цифру 2 и перейдите от 1 к 9, таким образом получится 10.
  • Теперь выполните 10 + 5, что даст 15. Оставьте 5 и перенесите 1 на следующий провод.
  • Теперь сложите 8 (7 + 1) и 4, и в результате получится 12.

Итак, результат будет 1252.

\ (\ следовательно \) Sum = 1252

Майк учится представлять числа на счетах.Можете ли вы сказать ему, какое число представлено на следующих счетах:

Решение

Бусины, представленные на счетах, имеют следующий вид:

  • 4 на месте
  • 2 в десятке
  • 1 раз в сотках
  • 3 в сотках

Итак, представленное число = 3124.

\ (\ следовательно \) Представленное число = 3124

Какие операции можно выполнять на счетах?

Решение

На счетах можно выполнять следующие операции:

  • Дополнение
  • Вычитание
  • Дивизион
  • Умножение

  • Как бы вы использовали счеты для умножения и деления?

Интерактивные вопросы

Вот несколько занятий для вас.Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

Подведем итоги

Мини-урок был посвящен увлекательной концепции счётов. Математическое путешествие по счетам начинается с того, что студент уже знает, и переходит к творческому созданию новой концепции в молодых умах. Сделано таким образом, чтобы не только было понятно и легко понять, но и навсегда осталось с ними.В этом заключается магия Куэмат.

О компании Cuemath

В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!

Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.

Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в которые мы, в Cuemath, верим.

Часто задаваемые вопросы (FAQ)

1. Что такое полная форма счеты?

Полная форма абака — это система «Изобилие бусинок, сложения и вычислений».

Это простое счетное устройство, состоящее из бусинок, размещенных в стержнях проволоки, заключенных в деревянную раму.

2. Чем полезны счеты в математике?

Abacus — это устройство, которое можно использовать для выполнения математических операций, таких как сложение, вычитание, умножение и деление.

Таким образом, это помогает сократить время при выполнении математических вычислений с большей эффективностью.

3. Как вы представляете числа на счетах?

Счеты — это устройство, которое можно использовать для счета, сложения, вычитания, умножения и т. Д.

Числа могут быть представлены как:

  • Крайний правый столбец — для своего места.
  • Следующий столбец используется для разряда десятков.
  • Третий столбец справа предназначен для разряда соток и так далее.

Что такое счеты?

Обновлено: 02.08.2020, Computer Hope

Альтернативно называемая счетной рамкой , счет — это механическое устройство, используемое для помощи человеку в выполнении математических вычислений и подсчета.

Кто построил первые счеты?

До сих пор неизвестно, кто построил первые счеты и когда они были построены. Есть свидетельства того, что счеты, использовавшиеся в Месопотамии, датируются 2700 годом до нашей эры.C., для использования с их шестидесятеричной системой счисления. Счеты также использовались в других ранних цивилизациях, включая китайскую, египетскую, греческую, персидскую и римскую цивилизации.

Почему использовались счеты?

До появления компьютеров, калькуляторов или даже арифметических операций с использованием бумаги и карандаша, счеты были наиболее совершенным устройством для вычисления чисел. До появления счётов единственными методами, которые люди должны были использовать для своих математических вычислений, были пальцы рук и ног или камни в земле.

Счеты все еще используются сегодня?

Да, даже сегодня в некоторых частях мира счеты все еще используются в качестве основного счетного устройства или в качестве резервного устройства для более современных счетных устройств.

Почему я должен изучать или обучать счетам?

Обучение работе со счетами помогает научить вас новому способу счета и тому, как складывать и вычитать, используя дополнительные числа. Научившись решать проблемы по-новому, вы сможете находить лучшие, а зачастую и более простые решения для всех видов проблем.

Как пользоваться счетами

Прежде чем научиться пользоваться счетами, осознайте, что существуют разные типы счетов. Например, классические счеты или китайские счеты имеют пять бусин внизу и две бусинки вверху. Современные счеты, японские счеты или соробан имеют четыре бусинки внизу и одну бусину вверху. В качестве примеров на этой странице мы используем современные счеты.

Верхние бусинки называются «Небесными бусами» и стоят пять в первом столбце.Нижние бусинки называются «Бусинки Земли», и каждая из них стоит одной в первом столбце. При перемещении бусинки к средней полосе (шкале счисления) она считается засчитанной, и когда ни одна бусинка не касается шкалы счисления, этот столбец равен нулю. Точки разделения и неокрашенные бусины различаются в зависимости от абака, но всегда используются для разделения чисел на наборы по три. Эти маркеры также могут отметить вашу первую позицию, если вы не хотите начинать отсчет с крайнего правого угла. Значения бусинок начинаются в крайнем правом столбце 1, которые имеют значение от 1 до 9.При движении справа налево значения бусинок увеличиваются до 10, 100, 1000 и т. Д.

Чтобы использовать счеты, положите их на ровную поверхность и установите на ноль, убедившись, что никакие бусинки не касаются счетной планки. Если у вас есть кнопка сброса, нажмите ее, чтобы сбросить бусинки. Чтобы считать на счетах, начните с крайней правой стороны абака и проведите большим пальцем одну земную бусину вверх до шкалы счисления. Одна бусинка, касающаяся шкалы счисления, делает счет равным 1. Сдвиньте еще три бусинки вверх, чтобы счет стал равным четырем (3 + 1 = 4).Поскольку современные счеты имеют только четыре земных бусины, если вы хотите сосчитать до пяти, вы должны переместить небесную бусину вниз к шкале счисления указательным пальцем. Одновременно переместите вниз все бусинки Земные. Если вы хотите, чтобы всего было семь, переместите две земные бусинки вверх до шкалы счисления (5 + 2 = 7).

Чтобы считать до более высоких чисел, двигайтесь дальше влево в зависимости от того, насколько высоко вы хотите считать. Например, изображение абака равно «283» с девятью бусинками, сдвинутыми к счетной планке.В третьем столбце (столбец 100) есть две бусины, рассчитанные на 200. Во втором столбце (столбец 10) есть небесная бусина, насчитывающая 50, и три земных бусины, рассчитанные на 30, что в сумме составляет 80. Наконец, первый столбец (единицы столбец) насчитывает три бисерины. Сложив все столбцы вместе (200 + 80 + 3), вы получите 283.

Как добавить с помощью счеты?

Чтобы прибавить к счетам, каждое число добавляется к счетам по слева направо . Например, если мы хотим добавить 200 + 123, переместите две Земные бусины в столбце 100 к шкале счисления для 200.Затем добавьте одну бусину Земли в столбец 100 для 100, 2 бусинки Земли в столбце 10 для 20 и, наконец, три бусины в столбце 1 для трех. После завершения счет будет равен 323.

Что делать, если в столбик недостаточно бусинок?

Когда у вас заканчиваются бусинки, вам нужно использовать дополнительные числа. См. Дополнительную информацию в разделе дополнительных номеров и список дополнительных номеров.

Как вычитать по счетам?

Простое вычитание на счетах похоже на сложение на счетах, введите ваше первое число, а затем вычтите из этого числа слева направо .Например, чтобы сделать 200 — 100, прибавьте 200 к счетам, переместив две Земные бусины вверх в столбце 100, затем вычтите 100 из столбца 100, чтобы получить в сумме 100.

Что делать, если не хватает бусин?

Если не хватает бусинок, чтобы убрать из столбца, используйте дополнительное число того, что вы пытаетесь вычесть. См. Дополнительную информацию и примеры в понимании дополнительных чисел.

Что такое дополнительные числа

Вообще говоря, «дополнения» — это любые два числа меньше десяти, которые в сумме дают десять.Они используются в вычислениях с участием более чем одного столбца. Очень важно запомнить пять наборов дополнительных чисел, содержащихся в рамке ниже. Они необходимы, если вы хотите выполнять все формы сложения и вычитания на счетах.

 9 и 1
8 и 2
7 и 3
6 и 4
5 и 5

Использование дополнительных чисел для сложения на счетах

Ниже приведен список шагов, как сложить числа с помощью счеты. Мы разбили эти шаги на маркированные списки, чтобы упростить их выполнение.

Кончик

При сложении, если в столбце недостаточно бусинок , вычтите дополнительное число из столбца и добавьте одну бусину в столбец слева.

Примечание

Многие из этих примеров вы, вероятно, сможете продумать в своей голове. Однако, следуя инструкциям на счетах, вы увидите все необходимые шаги.

Как добавить 4 + 7

  • Установите счет на четыре.
  • Вычтите три (дополнение семи) земных бусинок из столбца 1.
  • Добавьте одну бусину Земли в столбец десятков.
  • Итого должно быть 11 (10 + 1 = 11).

Как добавить 7 + 9

  • Установите счет на семь.
  • Вычтите одну (дополнение до 9) Земную бусину из столбца единиц.
  • Добавьте одну бусину Земли в столбец десятков.
  • Итого должно быть 16 (10 + 5 + 1 = 16).

Как добавить 19 + 6

  • Установите счет на 19.
  • Вычтите четыре (дополнение из шести) земных бусинок из столбца 1.
  • Добавьте одну бусину Земли в столбец десятков.
  • Итого должно быть 25 (20 + 5 = 25).

Как добавить 22 + 19

  • Установите счет на 22.
  • Вычтите одну (дополнение до девяти) Земную бусину из столбца 1.
  • Добавьте одну бусину Земли в столбец десятков.
  • Итого должно быть 31 (30 + 1 = 31).

Использование дополнительных чисел для вычитания на счетах

Ниже приведен список шагов по вычитанию чисел с помощью счеты.Мы разбили эти шаги на маркированные списки, чтобы упростить их выполнение.

Кончик

При вычитании, если в столбце недостаточно бусинок , добавьте дополнительное число к столбцу и вычтите одну бусину из столбца слева.

Как вычесть 10-6

  • Установите счет на 10.
  • Добавьте четыре (шесть) Земных бусинок в столбец 1.
  • Вычтите одну бусину из столбика десятков.
  • Всего должно быть четыре.

Как вычесть: 40-8

  • Установите счет на 40.
  • Добавьте две (восемь) бус Земли в столбец 1.
  • Вычтите одну бусину из столбика десятков.
  • Итого должно быть 32 (30 + 2).

Как вычесть 83-25

  • Установить счет на 83.
  • Вычтите две бисерины из столбика десятков.
  • Добавьте пять (дополнение из пяти) Небесных бусинок в столбец 1.
  • Вычтите одну бусину из столбика десятков.
  • Итого должно быть 58 (50 + 5 + 3).

Как вычесть 62-19

  • Установить счет на 62.
  • Вычтите одну бусину из столбика десятков.
  • Добавьте одну (дополнение из девяти) Земную бусину в столбец 1.
  • Вычтите одну бусину из столбика десятков. Для этого, поскольку столбец 10 равен 50 с Небесной бусиной, вычтите Небесную бусину и добавьте четыре Земных бусины.
  • Итого должно быть 43 (40 + 3).

Как вычесть 392-125

  • Установить счет на 392.
  • Вычтите одну бусину из столбца 100.
  • Добавьте одну (дополнение из девяти) Земную бусину в столбец десятков.
  • Вычтите две бисерины из столбика десятков.
  • Добавьте пять (дополнение пяти) Земных бусинок в столбец 1.
  • Вычтите одну бусину из столбика десятков.
  • Итого должно быть 267 (200 + 50 + 10 + 5 + 2).

Калькулятор

счётов в предложении | Примеры предложений по Кембриджскому словарю

Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.

Только каждый третий слышал о счетах .

Национальный полицейский компьютер будет представлять собой всего лишь счётов по сравнению с компьютером, необходимым для управления схемой национального удостоверения личности.

Я думаю, что кто-то убежал с abacus , так как схема явно будет стоить значительно дороже.

В этом интересном контексте он предположил, что abacus человек не имел сердца, сострадания или чувств.

У меня есть только простые счеты ; как это может быть?

Его особенно вознаграждают, если он предвидит это и производит, скажем, карманный калькулятор вместо счётов ; или даже в наши дни производит карманный компьютер.

Я не использовал логарифмическую линейку, калькулятор или счеты для вычислений, хотя до окончания обсуждения нам могут понадобиться счеты .

Перевернутая калаша украшает верх, на котором также изображены счеты с выступом .

Из

Википедия