Ментальная математика
Какую науку называют королевой?
Очень известная фраза «Математика-королева всех наук» была сказана великим немецким ученым Карлом Фридрихом Гауссом. Еще в детстве он удивлял всех своими способностями за секунды вычислять суммы чисел в пределах 100. Чем же помогли такие навыки юному математику?
Каким образом в 20 лет Гаусс уже получил степень доктора в университете г.Хельмштедт?
Его труды оказали большое влияние на развитие алгебры, теории чисел, математической физики, теории электричества, магнетизма и многих разделов астрологии.
Можно ли стать гением сегодня?
Если заниматься по традиционной системе образования, то это позволит развить левое полушарие мозга, чего будет достаточно для логического мышления.
Но если Вы заботливый родитель и планируете помочь своему ребёнку раскрыть весь потенциал, тогда внимательнее оцените новый метод в образовании, хотя и основанному на методиках более 3тыс.лет.
Более 5 миллионов вундеркиндов в 56 странах мира (от Канады до Австралии, от США до Японии) обучаются этому методу. Речь идёт о ментальной математике.
Что такое ментальная математика?
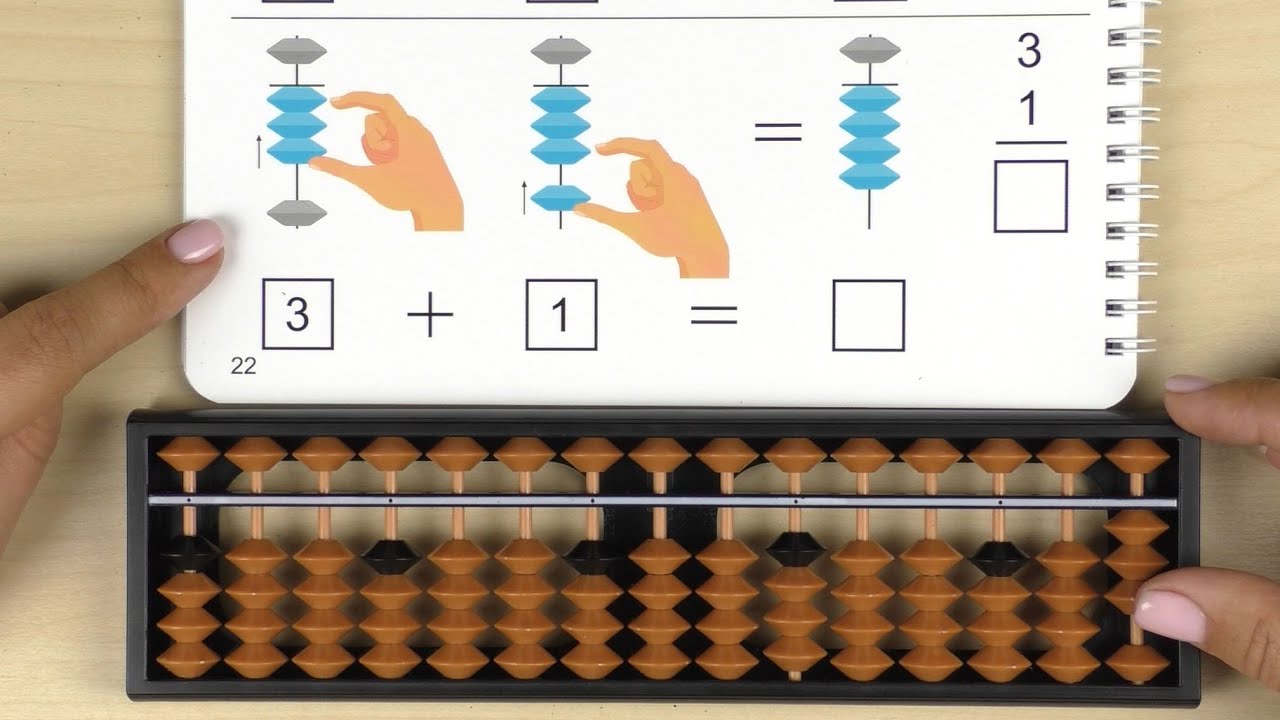
Ментальная математика- это китайская оригинальная методика развития интеллекта при помощи счёт АБАКУСа. У ребёнка во время игры на счётах происходит формирование умственных и творческих способностей, при этом побочным эффектом является мгновенный устный счёт.
АБАКУС
Материал из Википедии — свободной энциклопедии
Реконструкция римского абака
Аба́к (др.-греч. abacus — доска) — счётная доска, применявшаяся для арифметических вычислений приблизительно с V века до н. э. в Древней Греции, Древнем Риме и в Китае.
Доска абака была разделена линиями на полосы, счёт осуществлялся с помощью размещённых на полосах камней или других подобных предметов.
Камешек для греческого абака назывался псифос; от этого слова было произведено название для счёта —псифофория, «раскладывание камешков»
В чём заключается методика?
При освоении методики ваш ребенок использует 2 руки и задействует оба полушария мозга. На первом этапе обучения он использует счеты, на втором – визуальные картинки, а далее происходит волшебство – ребенок считает в уме, только воображая счеты перед собой. Только представьте скорость мышления такого ребенка!
Дети, занимающиеся в школах ABACUS, обгоняют взрослых и калькуляторы. После обучения ваш ребенок будет играючи выполнять все арифметические операции: сложение, вычитание, умножение, деление, с любыми числительными.
Работа на воображаемых счётах не зависит от языковых систем. В других похожих техниках учащимся приходится представлять числа, оперируя их названиями на том или ином языке. А воображаемые счёты-абак — задача полностью визуальная, и от языка никак не зависит.
Кому подходит эта методика?
Эта «психическая математика» подойдёт каждому от 4 лет до 14 лет, кто желает отточить свои навыки счёта в уме. В Китае этой методике обучают в детских садах. В Англии используют абакусы в профилактических целях — против болезни Альцгеймера, обучая людей преклонного возраста.
Сколько нужно заниматься?
В младших группах занятия проходят 2 раза в неделю по 45 минут, в старших- 1 раз в неделю-1,5 часа.
Период обучения зависит от поставленных вами целей. Если хотите, чтобы ребенок научился складывать и вычитать двузначные числительные, то достаточно 8-9 месяцев обучения. Но чтобы добиться действительно впечатляющих результатов и попробовать свои силы на международной олимпиаде по ментальному счёту, потребуется не один год напряжённой работы.
Вы захотели научить своего ребёнка ментальному счёту?
Добро пожаловать в ABACUS! Первый урок будет в подарок!
OSF | Реформа интернета.
Wiki <p>Реформа интернета.</p>
<p>Упорядочивание нейронной структуры мозга происходит в процессе межличностного и прочих форм взаимодействия, и овладения средствами коммуникации, одним из которых является язык, структура или упорядоченность которого основаны на ассоциациях ментальных объектов, называемых впечатлениями, образами, символами, понятиями, являющимися элементами памяти {1}. То, как эти объекты связаны между собой, определяет наше поведение, мировозрение и понимание. Внешним выражением этих связей является речь, посредством которой происходит обмен ментального содержания и в идеальном случае взаимопонимание и сотрудничество. </p>
<p>Географическая обособленность популяций людей стала причиной многообразия языков. Хотя структурный принцип различных языков одинаков, и они синонимичны друг другу, условием понимания является не только владение определённым языком, но и понятийная идентичность слов и смыслов в речи. </p>
<p>Развитие письменной фиксации разговорной речи, появление сначала рукописных книг, а затем книгопечатания, позволило стереотипизирование или стереотипизацию понятийной идентичности слов, что происходит как в словарях, так и контекстуально в книгах различного содержания. Хотя стереотипизирование или стереотипизация понятий имеет свои негативные стороны, и может являться как источником, так и симптомом психических заболеваний, потери связи с реальностью {2}, оно является системной необходимостью всякого языка.</p>
<p>Традиция книгопечатания связана с производством текстов, подвергающихся их содержательной проверке, что опять же имеет свои недостатки, например возможность необоснованной цензуры {3}, однако эта традиция позволила создать то, что является основой современной системы образования (также имеющей свои недостатки), мяжязыковой коммуникации, и научного знания. </p>
<p>Интернет, 30–летие которого недавно отмечалось {4}, привнёс в вышеуказанную традицию беспорядок, некоторые аспекты которого я описывал в 2011 году {5–6}.
authors
authors:Peregrine Hordern, Nicholas Purcell.The Corrupting Sea: A Study of Mediterranean History.book</p>
<p>Адрес книги в интернете:</p>
<p>pub:Blackwell.The Corrupting Sea: A Study of Mediterranean History.book</p>
<p>Пример 4. Публикация: Nguyen, T., Carnevale, J. J., Scholer, A. A., Miele, D. B., & Fujita, K. (2019). Metamotivational knowledge of the role of high-level and low-level construal in goal-relevant task performance. Journal of Personality and Social Psychology, 117(5), 879-899. </p>
<p>Информация об этой публикации, но не сама публикация доступна в интернете по следующим адресам:</p>
<p><a href=»https://www.ncbi.nlm.nih.gov/pubmed/31120290″ rel=»nofollow»>https://www.ncbi.nlm.nih.gov/pubmed/31120290</a> <br>
<a href=»https://doi.org/10.1037/pspa0000166″ rel=»nofollow»>https://doi.org/10.1037/pspa0000166</a> <br>
<a href=»https://psycnet.apa.org/doiLanding?doi=10.1037%2Fpspa0000166″ rel=»nofollow»>https://psycnet.apa.org/doiLanding?doi=10.1037%2Fpspa0000166</a> <br>
<a href=»https://psycnet.apa.org/record/2019-28590-001″ rel=»nofollow»>https://psycnet.apa.org/record/2019-28590-001</a> The accepted manuscript version of this article will be publicly available on 05/22/2020.</p>
<p>Поскольку префиксы https://www. бессмысленны и избыточны в адресе, так же как и номер doi, они в референции и адресе, написанных по новым правилам, отсутствуют:</p>
<p>journal:Journal of Personality and Social Psychology/2019/117/5/Metamotivational knowledge of the role of high-level and low-level construal in goal-relevant task performance. Tina Nguyen, Jessica J. Carnevale, Abigail A. Scholer, David B. Miele, Kentaro Fujita.authors</p>
<p>journal:ISSN.0022-3514/year.2019/volume.117/number.5/pages.876–899.pdf <br>
journal:ISSN.0022-3514/year.2019/volume.117/number.5/pages.876–899.article <br>
pub:<a href=»http://psycnet.
apa.org/record/2019-28590-001″ rel=»nofollow»>psycnet.apa.org/record/2019-28590-001</a></p>
<p>Сходным образом возможна адресация страниц различного содержания в интернете.</p>
<p>Пример 5. „Издательство «Наука» (Академический научно-издательский, производственно-полиграфический и книгораспространительский центр Российской академии наук «Издательство „Наука“», сокращённое наименование – ФГУП «Издательство „Наука“») – советское и российское академическое издательство книг и журналов. Крупнейшее в СССР и в мире (в 1982 году) научное издательство. На логотипе издательства «Наука» изображён первый искусственный спутник Земли и раскрытая книга. В 2019 году находилось на пороге банкротства.“</p>
<p>Цитата происходит из страницы Википедии, имеющей следующий адрес:</p>
<p><a href=»https://ru.wikipedia.org/wiki/%D0%9D%D0%B0%D1%83%D0%BA%D0%B0_(%D0%B8%D0%B7%D0%B4%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D1%81%D1%82%D0%B2%D0%BE)» rel=»nofollow»>https://ru.wikipedia.org/wiki/%D0%9D%D0%B0%D1%83%D0%BA%D0%B0_(%D0%B8%D0%B7%D0%B4%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D1%81%D1%82%D0%B2%D0%BE)</a> или <br>
<a href=»https://ru.wikipedia.org/wiki/Наука_(издательство)» rel=»nofollow»>https://ru.wikipedia.org/wiki/Наука_(издательство)</a></p>
<p>Информация об издательстве в стандартизированном виде:</p>
<p>изд:Наука.РАН <br>
РАН:Наука.изд </p>
<p>а страница в интернете представима следующим образом:</p>
<p>изд:ру.википедия.орг/вики/Наука.изд</p>
<p>Однако кроме страницы, посвящённой издательству Российской академии наук „Наука“, имеются другие страницы, где слово наука употребляется в качестве названия:</p>
<p>Пример 6. Наука (значения) <br>
<a href=»https://ru.wikipedia.org/wiki/Наука_(значения)» rel=»nofollow»>https://ru.wikipedia.org/wiki/Наука_(значения)</a> <br>
Наука может означать: <br>
Наука — сфера человеческой деятельности. <br>
«Наука» — один из предполагаемых модулей Российского сегмента Международной космической станции. <br>
«Наука» — стадион в Москве. <br>
«Наука» — стадион в Ивано-Франковске. <br>
«Наука» — российское научно-производственное объединение авиационно-космической отрасли. <br>
«Наука» — российский круглосуточный телеканал о достижениях науки и техники. <br>
«Наука» — название советского баскетбольного клуба «Буревестник» из Ленинграда в 1953—1954 годах. <br>
Издательства
«Наука» — издательство Академии наук, основано в 1923 году. <br>
«Наука» — бывшее название казахстанского издательства «Гылым» (основано в 1946 году). <br>
Топонимы <br>
Наука — хутор в Перелюбском районе Саратовской области. <br>
Наука — микрорайон (посёлок) в Томске. <br>
Сложные термины <br>
Математические науки <br>
Естественные науки <br>
Технические науки <br>
Гуманитарные науки <br>
Социальные науки</p>
<p>Поскольку слово наука может означать различные объекты, адрес вышеупомянутой страницы Наука_(значения) по новым правилам пишется следующим образом:</p>
<p>изд:ру.википедия.орг/вики/Наука.лексема</p>
<p>Прежний и новый адрес страницы о науке как сфере человеческой деятельности:</p>
<p><a href=»https://ru.wikipedia.org/wiki/Наука» rel=»nofollow»>https://ru.wikipedia.org/wiki/Наука</a> <br>
изд:ру.википедия.орг/вики/Наука.знание</p>
<p>То же самое в отношении предполагаемого модуля Международной космической станции, стадиона, научно-производственного объединения авиационно-космической отрасли, телеканала, спортивного клуба, издательства «Гылым», топонимов:</p>
<p><a href=»https://ru.wikipedia.org/wiki/Наука_(модуль_МКС)» rel=»nofollow»>https://ru.wikipedia.org/wiki/Наука_(модуль_МКС)</a> <br>
изд:ру.википедия.орг/вики/Наука.модуль</p>
<p><a href=»https://ru.wikipedia.org/wiki/Наука_(стадион,_Москва)» rel=»nofollow»>https://ru.
wikipedia.org/wiki/Наука_(стадион,_Москва)</a> <br>
изд:ру.википедия.орг/вики/Наука.стадион.Москва.город</p>
<p><a href=»https://ru.wikipedia.org/wiki/Наука_(стадион,_Ивано-Франковск)» rel=»nofollow»>https://ru.wikipedia.org/wiki/Наука_(стадион,_Ивано-Франковск)</a> <br>
изд:ру.википедия.орг/вики/Наука.стадион.Ивано-Франковск.город</p>
<p><a href=»https://ru.wikipedia.org/wiki/НПО_«Наука»» rel=»nofollow»>https://ru.wikipedia.org/wiki/НПО_«Наука»</a> <br>
изд:ру.википедия.орг/вики/Наука.НПО.ПАО</p>
<p><a href=»https://ru.wikipedia.org/wiki/Наука_(телеканал)» rel=»nofollow»>https://ru.wikipedia.org/wiki/Наука_(телеканал)</a> <br>
изд:ру.википедия.орг/вики/Наука.тв</p>
<p><a href=»https://ru.wikipedia.org/wiki/Буревестник_(баскетбольный_клуб,_Ленинград)» rel=»nofollow»>https://ru.wikipedia.org/wiki/Буревестник_(баскетбольный_клуб,_Ленинград)</a> <br>
изд:ру.википедия.орг/вики/Буревестник.клуб.Ленинград.город</p>
<p><a href=»https://ru.wikipedia.org/wiki/Гылым» rel=»nofollow»>https://ru.wikipedia.org/wiki/Гылым</a> <br>
изд:ру.википедия.орг/вики/Гылым.изд</p>
<p><a href=»https://ru.wikipedia.org/wiki/Наука_(хутор)» rel=»nofollow»>https://ru.wikipedia.org/wiki/Наука_(хутор)</a> <br>
изд:ру.википедия.орг/вики/Наука.хутор</p>
<p>изд:ру.википедия.орг/вики/Наука.топоним</p>
<p><a href=»https://ru.wikipedia.org/wiki/Академгородок_(Томск)#Современность» rel=»nofollow»>https://ru.wikipedia.org/wiki/Академгородок_(Томск)#Современность</a> <br>
изд:ру.википедия.орг/вики/Академгородок.Томск#Современность</p>
<p>Поскольку „естественные науки (устар.естественная история, от «естество» или природа) – науки, изучающие природу (понимаемую в широком смысле как материальный мир Вселенной)“, а „множество отраслей естественных наук объединено в систему наук – естествознание“, то соответствующие адреса имеют следующее написание:</p>
<p><a href=»https://ru.
wikipedia.org/wiki/Естественные_науки» rel=»nofollow»>https://ru.wikipedia.org/wiki/Естественные_науки</a> <br>
изд:ру.википедия.орг/вики/Естествознание.наука</p>
<p>Математику традиционно относят к естественным наукам, поэтому пишем:</p>
<p><a href=»https://ru.wikipedia.org/wiki/Математика» rel=»nofollow»>https://ru.wikipedia.org/wiki/Математика</a> <br>
изд:ру.википедия.орг/вики/Математика.наука</p>
<p>Поскольку наука отличается от техники тем, что техника является реализацией научного знания, адрес соответствующей страницы Википедии переформатируется по новым правилам:</p>
<p><a href=»https://ru.wikipedia.org/wiki/Технические_науки» rel=»nofollow»>https://ru.wikipedia.org/wiki/Технические_науки</a> <br>
изд:ру.википедия.орг/вики/Техника.знание</p>
<p>Выражение „гуманитарные науки“ является симптомом отсутствия науки о человеке, на что я неоднократно обращал внимание публики. Так называемые „гуманитарные науки“, англ. humanities, изучают разрозненные факты одного феномена и его производных, не будучи в состоянии сложить их в одну картину, понять и объяснить, что есть человек и человечность, как становятся человеком, и как создать науку о человеке, т.е. человекознание. Поэтому „гуманитарные науки“ я заменяю на человекознание:</p>
<p><a href=»https://ru.wikipedia.org/wiki/Гуманитарные_науки» rel=»nofollow»>https://ru.wikipedia.org/wiki/Гуманитарные_науки</a> <br>
изд:ру.википедия.орг/вики/Человекознание.наука</p>
<p>а так называемые социальные или общественные науки заменяются обществоведением, обществознанием, или социологией:</p>
<p><a href=»https://ru.wikipedia.org/wiki/Общественные_науки» rel=»nofollow»>https://ru.wikipedia.org/wiki/Общественные_науки</a> <br>
изд:ру.википедия.орг/вики/Социология.наука</p>
<p>Предложенная схема применима для описания любых других объектов в интернете, что я продемонстрирую нижеследующими примерами.
</p>
<p>Пример 7. Общественный фонд города Новотроицка. {11}</p>
<p>Однозначное определение города Новотроицка:</p>
<p>город:Новотроицк <br>
Новотроицк.город</p>
<p>Соответственно этому определению, общественный фонд города Новотроицка будет иметь форму:</p>
<p>город:Новотроицк.фонд <br>
фонд:Новотроицк.город</p>
<p>Пример 8. Город New York.</p>
<p>Адрес города New York в интернете:</p>
<p><a href=»http://www.nyc.gov» rel=»nofollow»>http://www.nyc.gov</a> </p>
<p>Доменное имя .gov для меня ассоциируется со словом говно, хотя для человека, чей родной язык английский, это неочевидно. В смысловой и осмысленной интерпретации город New York должен отображаться в комбинации с метаименем city, т.е. город, как в вышеприведённых примерах:</p>
<p>city:New York <br>
New York.city</p>
<p>Адреса органов самоуправления города New York в настоящее время: </p>
<p><a href=»https://portal.311.nyc.gov/category/?id=311-3″ rel=»nofollow»>https://portal.311.nyc.gov/category/?id=311-3</a> Courts and Law <br>
<a href=»https://portal.311.nyc.gov/category/?id=311-10″ rel=»nofollow»>https://portal.311.nyc.gov/category/?id=311-10</a> Health <br>
<a href=»https://portal.311.nyc.gov/category/?id=311-52″ rel=»nofollow»>https://portal.311.nyc.gov/category/?id=311-52</a> City Government <br>
<a href=»https://council.nyc.gov» rel=»nofollow»>https://council.nyc.gov</a> New York City Council <br>
<a href=»https://portal.311.nyc.gov/article/?kanumber=KA-01226″ rel=»nofollow»>https://portal.311.nyc.gov/article/?kanumber=KA-01226</a> Mayor</p>
<p>В подобном написании я усматриваю бессмыслицу: к <a href=»http://nyc.gov» rel=»nofollow»>nyc.gov</a> непонятным образом прибавилось portal.311, а категории портала 311 определяются через вопросительный знак и следующим за ним кодом.
Что есть портал 311 разъясняется в интернете:</p>
<p><a href=»https://www.ny.gov/agencies/nyc-311″ rel=»nofollow»>https://www.ny.gov/agencies/nyc-311</a> 311 provides access to New York City government services through eight platforms: Call Center, Social Media, Mobile App, Text, Video Relay Service and TTY/text telephone. <br>
<a href=»https://portal.311.nyc.gov/» rel=»nofollow»>https://portal.311.nyc.gov/</a> NYC311 – The Official Website of the City of New York.</p>
<p>Согласно предлагаемой схеме наименования объектов в интернете органы местного самоуправления города New York имеют следующую форму:</p>
<p>city:New York.council – City Council of New York. <br>
council:New York.city – City Council of New York.</p>
<p>city:New York.justice – Courts and Law, i.e. judicature or judiciary. <br>
justice:New York.city – Courts and Law, i.e. judicature or judiciary.</p>
<p>city:New York.healthcare – Public health care. <br>
healthcare:New York.city – Public health care.</p>
<p>city:New York.policy – Public policy. <br>
policy:New York.city – Public policy.</p>
<p>city:New York.mayor – Mayor of New York. <br>
mayor:New York.city – Mayor of New York.</p>
<p>Соответствующие адреса названных объектов в интернете определяются в зависимости от источника публичной информации:</p>
<p>pub:New York.city/council/… <br>
council:New York.city/…</p>
<p>pub:New York.policy/justice/… <br>
policy:New York.city/justice/…</p>
<p>и т.д.</p>
<p>Для реализации предложенной схемы наименований осталось только общими усилиями создать базу стандартных имён. Однако реформа интернета и преобразование его в средство общения и служения обществу требует также других мер. К этим мерам относится передача определённых имён в неотчуждаемое владение, чтобы их собственники безусловно и беспрепятственно могли осуществлять их право публикации, т.
е. публичного высказывания и выражения их мыслей, что также важно для документографии. Другой мерой должно стать упразднение всей сложившейся системы управления интернетом, т.е. бюрократии, после чего техническим службам будут делегированы обязанности по обеспечению его функционирования с учётом высказанной критики.</p>
<p>Интернет происходит от телефонной связи, которая обеспечивала передачу голоса. Телефонный разговор был экспромтом, он появлялся и исчезал одновременно с произнесением и восприятием звуков. Его транзитность прекратилась с появлением методов фиксации звуковой записи и соответствующих технических средств – магнитофонов. Этот же метод был использован для записи и кодирования других видов информации и их обработки счётными машинами (СМ), т.е. компъютерами (от compute считать). Новшество интернета состояло в использовании СМ для создания, передачи, приёма, фиксации, и использования информации, которая стала доступной не только участникам диалога и секретным службам, тайно прослушивавшим телефонные разговоры, но также прочей публике. </p>
<p>Попытки создания метаинтернета, т.е организаций, позиционирующих себя над ним и осуществляющих управление им (в качестве рулевого, κυβερνήτης), противоречат праву свободного высказывания и выражения мыслей в других возможных формах, а также праву быть услышанным. Именно поэтому всякая регуляция интернета, нарушающая права индивидуума, непозволительна.</p>
<p>Список цитированных источников.</p>
<ol>
<li>
<p>А. Полеев. Человек – это память. Enzymes, 2020.
<a href=»http://enzymes.at/download/memory.pdf» rel=»nofollow»>http://enzymes.at/download/memory.pdf</a></p>
</li>
<li>
<p>A. Poleev. Deutsche Krankheit. Enzymes, 2019.
<a href=»http://enzymes.at/download/Schizophrenie.pdf» rel=»nofollow»>http://enzymes.at/download/Schizophrenie.pdf</a> </p>
</li>
<li>
<p>A. Poleev. A review on a peer review.
Enzymes, 2016.
<a href=»http://enzymes.at/download/review.pdf» rel=»nofollow»>http://enzymes.at/download/review.pdf</a> </p>
</li>
<li>
<p>30th Anniversary of the World Wide Web
https://home.cern/events/web30 </p>
</li>
<li>
<p>А. Полеев. Универсальный стандарт метаданных. Enzymes, 2011.
<a href=»http://enzymes.at/download/metadata.pdf» rel=»nofollow»>http://enzymes.at/download/metadata.pdf</a> </p>
</li>
<li>
<p>A. Poleev. Universal Metadata Standard. Scientific and Technical Information Processing, 2011, Vol. 38, No. 2, pp. 119–122.</p>
</li>
<li>
<p>Thing – The most generic type of item according to vocabulary of the „semantic web“.
<a href=»https://schema.org/Thing» rel=»nofollow»>https://schema.org/Thing</a></p>
</li>
<li>
<p>„In the next step, the Semantic Web will break out of the virtual realm and extend into our physical world. URIs can point to anything, including physical entities, which means we can use the RDF language to describe devices such as cell phones and TVs. Such devices can advertise their functionality – what they can do and how they are controlled – much like software agents. Being much more flexible than low-level schemes such as Universal Plug and Play, such a semantic approach opens up a world of exciting possibilities.“ Tim Berners-Lee, James Hendler and Ora Lassila. The Semantic Web. A new form of Web content that is meaningful to computers will unleash a revolution of new possibilities. Scientific American, May 2001, p. 29-37.</p>
</li>
<li>
<p>Assembly – About this site.
<a href=»http://assembly.re/pages/about.html» rel=»nofollow»>http://assembly.re/pages/about.html</a> </p>
</li>
<li>
<p>For the attention of ICANN, registry operators and registrars.
http://constitution.fund/letters/internet.pdf </p>
</li>
<li>
<p>О месте и роли общественных фондов в структуре органов местного самоуправления.
http://constitution.fund/letters/funds.pdf </p>
</li>
</ol>Технологии интернет-обучения, ОЗО, 2013-14
На этой странице размещены задание лабораторных работ по дисциплине «Технологии интернет-обучения» для студентов заочной формы обучения профилей «Информатика» и «Математика».
Профиль «Математика»
Задание 1
- Изучить интерфейс и возможности программы Geogebra.
Разработать электронные ресурсы по математике (доказательства геометрических теорем, построения графиков и т.д.) с помощью программы GeoGebra.
GeoGebra — свободная кроссплатформенная динамическая математическая среда для всех уровней образования, включающая в себя геометрию, алгебру, таблицы, графы, статистику, арифметику.
Материалы:
Задание 2
Разработать пример учебного материала по математике в одном из следующих сервисов:
На выполнение задания отводится 3 пары, на зачетном занятии проводится защита разработанных материалов.
Профиль «Информатика»
Задание
Выбрать тему из школьного курса информатики или математики.
По выбранной теме разработать не менее двух дидактических материалов используя следующие сервисы сети Интернет:
Глог (glog) — графический блог (graphical blog).
При разработке дидактических материалов необходимо использовать различные сервисы сети Интернет!На выполнение задания отводится 3 пары, на зачетном занятии проводится защита разработанных материалов.
Наши работы
Справочные материалы
Веб 2.
0 — это обозначение новых течений, нового этапа эволюции в Интернете. Сервисы Веб 2.0 — это современные средства, сетевое программное обеспечение, поддерживающее групповые взаимодействия. Они позволяют пользователям Интернета размещать собственную информацию и выстраивать сеть личных отношений в виртуальном пространстве.
При разработке презентации учитывайте требования к оформлению и компоновке материала.
Дополнительно про дидактические материалы.
Примеры
Лента времени «История развития Интернета»
Пример prezi-презентации
Пример интерактивного плаката
Пример карты знаний
Создайте свой собственный mind карты при MindMeister
Назад: Технологии интернет-обучения
Грех телепортации: почему будущее и религия плохо совместимы
Так вот, в ближайшем будущем и эту проблему можно будет решить. Гены, как мы теперь знаем, — это практически конструктор лего. У всех земных организмов они схожи, и при желании скоро можно будет собрать самого настоящего человека, вообще не прибегая к биоматериалам, полученным от гомо сапиенс, а надергав их из всяких прочих живых существ — бабочек там, птичек, рыбок и чертополоха. И нате вам: человек канонически безгрешный!
Неудивительно, что еще католический богослов Клайв Стейплз Льюис уже начал стелить на этом неприятном месте соломку, намекая, что у всех животных тоже было свое грехопадение, еще пораньше человеческого. И да, у растений тоже. Не говоря уж о микробах. Подробностей мы не знаем, но достаточно посмотреть на их образ жизни, чтобы в этом убедиться.
И тем не менее любые манипуляции с геномом человека вызывают у большинства конфессий страшную агрессию. И прямо, и опосредованно именно этой области знания религиозные группы вставляют особенно большие палки в слишком шустрые колеса.
Если с неба не велят
Переливание крови.В Библии не раз сказано, что душа любого существа находится в его крови, поэтому кровь в пище должна быть запрещена. Мусульмане и иудеи придерживаются правила, христиане в массе своей на него наплевали. Но среди протестантских церквей есть те, кто очень серьезно относится к Ветхому Завету. Например, «Свидетели Иеговы» не признают переливание крови и ее компонентов, отказываются от него даже под угрозой гибели. Поэтому ежегодно в мире заводится десяток уголовных дел на родителей-иеговистов, препятствующих лечению своих несовершеннолетних детей.
Спиртосодержащие лекарства и ислам. Как известно, первая же капля вина губит мусульманина — по крайней мере, пророк на этом настаивал. Поэтому в клиниках, придерживающихся халяльных норм, спиртосодержащие препараты запрещены, в том числе простые дезинфицирующие. Существует даже особая отрасль исламской фармацевтики, которая придумывает безалкогольные альтернативы спиртосодержащей лекарственной продукции.
Теория эволюции. Католики уже признали теорию «божественной эволюции», православие не имеет единого мнения по этому вопросу (хотя противников эволюции среди православных деятелей немало — достаточно вспомнить депутата Виталия Милонова, который требует запретить преподавать в школах «обезьянью ересь»), а вот протестанты в массе своей креационисты, то есть обязаны свято верить, что всех животных Господь создал за один день шесть тысяч лет назад и никаких изменений и развития их не запланировал. Поэтому в половине штатов США преподавание теории эволюции в школах либо запрещено, либо разрешено, но с параллельным обязательным знакомством школьников с идеями креационизма.
Эвтаназия. Помочь смертельно больному и в муках умирающему человеку уйти из жизни легко и безболезненно? Пока человечество воевало, церковь мало вмешивалась в этот вопрос, и мизерикордии (ножи для милосердного добивания тяжелораненых) превесело сверкали на полях после сражений.
Сегодня же все христианские церкви ревностно стоят на страже интересов души, которая очищается страданием и должна быть спасена от страшнейшего греха — самоубийства. Светская этика тоже не имеет однозначного ответа на этот тяжелый вопрос: можно ли помочь уходящему или нужно всеми способами продлевать его мучения?
Изменение личности
Сегодня нейрокоррекцией называют область психологии, специализирующуюся на попытках улучшить состояние людей с серьезными проблемами в психике. Нейрокоррекция будущего будет производиться не психологами, а специалистами, умеющими влиять на работу нейронов. Нейробиология — одна из самых стремительно развивающихся отраслей знания, буквально ежегодно тут происходят революции, пусть даже не очень понятные для далеких от этих сфер граждан.
Создание в 90-х годах XX века аппаратов МРТ, машин, умеющих видеть мозговую активность, перенесло нас в другую эпоху (правда, мы пока еще этого не заметили). Можно с уверенностью прогнозировать, что уже в ближайшие десятилетия люди научатся изменять личность путем перенастройки нейронных связей в мозге или даже закачивать в него нужную информацию, скопированную из другого мозга. Самые первые шажки тут уже делаются.
★ Устный счёт — Вики .. | Информация
4. Феноменальные счетчики.
(Phenomenal counters)Феномен особых способностей в устном счете встречается с давно. как вы знаете, у них было много ученых, в частности, Андре Ампер и Карл Гаусс. впрочем, умение считать является общим для многих людей, чья профессия была далека от математики и науки в целом.
До второй половины XX века на сцене был популярен выступления специалистов в устном счете. иногда они устраивали между собой соревнования, занимал в том числе и в стенах уважаемых учебных заведениях, включая Московский государственный университет имени М. В университет.
Среди известных русских «супер счётчиков»:
- Г-Н Кутуков (Mr.
Kutukov) — «человек-календарь». - Дэвид Голдстейн. (David Goldstein)
- А. В. Некрасовская (A. V. Nekrasov) — «человек-компьютер».
- Игорь Селюков. (Igor Selyukov)
- Аарон Chikvashvili (Aaron Chikvashvili) — «чудо-счётчик».
- Горы Яшков Юрий Гаврилович.
- Арраго. (Arrago)
Kutukov) — «человек-календарь».Среди иностранных:
- Борислав Gadjanski. (Borislav Gadjanski)
- Yusnier Виера (Yusnier VIERA) — кубино-американский математик, феноменальный счетчик мировой рекордсмен в области устного перевода в календарном исчислении.
- Уильям Кляйн. (William Klein)
- Жак Иноди. (Jacques Inode)
- Луи Флери. (Louis Fleury)
- Томас Фуллер. (Thomas Fuller)
- Шакунталу Деви. (Sakuntala Devi)
- Мадемуазель Осака. (Mademoiselle Osaka)
- Морис Добер. (Maurice Dober)
- Урания Diamandi. (Urania Diamandi)
Хотя некоторые эксперты настаивают, что дело во врожденной способности, другие аргументированно доказывали обратное: «дело не только в каких-то исключительных, «феноменальных» способностями и знаниями математических принципов, позволяет быстро «вычислить» и охотно раскрывали эти законы.
Истина, как обычно, был на какой-то «золотой середине» сочетание природных способностей и грамотного, трудолюбивого их пробуждения, взращивания и использования. те, кто по Трофиму Лысенко, уповают исключительно на волю и напористость, со всеми уже хорошо известными способами и приемами устного счета обычно при всех усилиях не поднимаются выше очень средних достижений. более того, настойчивые попытки «хорошенько нагрузить» мозг такие задачи, как устный счет, шахматы, и слепой т. п. может легко привести к переоценивайте свои возможности и значительное снижение умственной работоспособности, памяти и здоровья, а в самых тяжелых случаях и шизофрении. С другой стороны, и одаренные люди в неизбирательное применение своим талантам в области психического математике быстро «перегорают» и перестают быть в состоянии длительно и устойчиво и показать значительные достижения.
История ментальной арифметики
ИСТОРИЯ МЕНТАЛЬНОЙ АРИФМЕТИКИ
Ментальная арифметика – методика достаточно молодая и в то же время очень древняя. Началом ее существования можно считать изобретение счетной доски (суаньпань) в Китае более 5 тысяч лет назад. Те древние счеты представляли собой дощечку со специальными обозначениями и песком, разделенным на строки. Чуть позже в Египте, Древней Греции и Древнем Риме появились аналогичные приспособления для арифметических вычислений. Они больше походили на современные счеты, поскольку подсчет велся на доске не с помощью песка, а с использованием камней или косточек.
Известно, что в России в конце XV столетия были придуманы так называемые «русские счеты». Их особенностью было то, что в них применялась десятичная система счисления. В XVI веке китайской счетной доской суаньпань заинтересовались в Японии. Японские счеты использовали пятеричную систему счисления и назывались соробан.
Современные японцы считают, что и сегодня обучение счету с использованием соробана имеет ряд неоспоримых преимуществ по сравнению с традиционным подсчетом на бумаге. Этот метод тренирует мозг, увеличивая количество нейронных связей, и способствует развитию интеллекта и творческих способностей.
На протяжении нескольких столетий соробан активно применяется для обучения детей в странах Азии. В Европе и Америке активно заинтересовались соробаном в XXI веке. А в нашей стране первые школы обучения ментальной арифметике появились в 2013 году.
Соробан неоднократно видоизменялся и совершенствовался. В настоящее время японские счеты используются в том виде, в котором их применяли в торговле в 40-х годах прошлого века. Счеты представляют собой коробку прямоугольной формы с 13 рядами косточек. Каждый ряд содержит по 5 косточек. 4 нижних косточки, называемые «земными», имеют значение «один». Верхняя же косточка – «небесная» — соответствует «пяти».
Способ вычислений с помощью счетов внесен в список устного и нематериального культурного наследия ЮНЕСКО.
И действительно, счетная доска – это уникальное изобретение человечества. Она позволила древним людям быстро складывать, вычитать, перемножать и делить многозначные числа, а также извлекать квадратные и кубические корни.
Соробан поможет вашему ребенку повысить уровень интеллекта, раскрыть творческие способности, улучшить внимание, память и школьные отметки!
Алан Тьюринг — человек, у которого отобрали право любить
- Александр Кан
- обозреватель по вопросам культуры<br> Русской службы Би-би-си
Автор фото, Studiocanal
Подпись к фото,Алан Тьюринг (Бенедикт Камбербатч), его жена Джоан (Кира Найтли) и их товарищи по группе, взломавшей нацистскую шифровальную машину «Энигма». Кадр из фильма «Игра в имитацию»
«Никто другой не внес такого же вклада в нашу победу в войне», — Уинстон Черчилль, охарактеризовавший таким образом британского математика Алана Тьюринга, лучше других знал цену победы и цену усилий разных людей в этой победе.
Суперпопулярный сейчас после «Шерлока Холмса» Бенедикт Камбербатч в главной роли, не менее популярная Кира Найтли в роли соратницы и жены Тьюринга – самые яркие звезды британского кино призваны привлечь усиленное внимание к и без того предельно увлекательной истории жизни ученого в выходящем в эти дни на британские экраны фильме «Игра в имитацию».
Кто такой Тьюринг?
Автор фото, studiocanal
Подпись к фото,Давление было чудовищным. Однажды Тьюринга чуть не арестовали по подозрению в шпионаже. Кадр из фильма «Игра в имитацию»
Игра в имитацию, или имитационная игра — один из математических, логических приемов, разработанных Тьюрингом для первых изобретенных им пракомпьютеров. Этот и многие другие методы работы с первыми самыми примитивными компьютерами помогли Тюрингу и его группе раскрыть сверхсекретный код германского вермахта.
В 1939 году, вскоре после начала войны Тьюринг, работавший тогда в Кембриджском университете, был привлечен к работе над раскрытием кода немецкой шифровальной машины «Энигма». Работа была сверхсекретной, велась на закрытой базе Блетчли-парк в графстве Бэкингемшир в центре Англии. Проблема с кодировкой «Энигмы» состояла в том, что система кодов менялась каждый день, и наутро все достигнутые за день результаты шли в корзину.
Работа продолжалась несколько лет в условиях чудовищного давления со стороны высшего руководства британской армии и контрразведки. Тьюринг был на грани увольнения и однажды даже ареста — по подозрению в шпионаже в пользу Советов, и лишь личное вмешательство Черчилля, к которому уверенный в правильности избранного метода ученый обратился за поддержкой, спасло его и его группу.
Автор фото, Science Photo Library
Подпись к фото,Алан Тьюринг — не кинематографический, а реальный — бежит марафонскую дистанцию в 1946 году
В то же время Тьюринг — каким мы видим его в фильме — был человек нелегкий, с людьми ладил трудно и даже внутри его собственной группы сплошь и рядом возникали трения, пока, наконец, код не был взломан.
И его работа, и сам Тьюринг оставались строго засекречены и после войны.
Преследование и посмертное помилование
В 1952 году, работая уже в Манчестере, гомосексуалист Тьюринг был арестован и подвергнут уголовному преследованию за тогда еще противозаконную связь с 19-летним молодым человеком. Его поставили перед суровым выбором – тюрьма или «лечение» эстрогеном, процесс, по сути своей являвшийся ничем иным как химической кастрацией.
Через год после такого «лечения» в 1954 году, за две недели до своего 42-го дня рождения Тьюринг принял дозу цианистого калия. Расследование постановило, что смерть наступила в результате самоубийства.
Автор фото, studiocanal
Подпись к фото,Даже следователь, допрашивавший Тьюринга по делу о гомосексуализме, признал его «человеком чести»
В 2009 году тогдашний премьер-министр Гордон Браун принес официальные публичные извинения от имени правительства Великобритании за «чудовищное обращение», которому был подвергнут ученый.
В 2013 году — лишь совсем недавно — специальным указом королевы Елизаветы Второй Тьюрингу было даровано посмертное помилование.
История в кино
«Игра в имитацию» — не первый художественный фильм, посвященный Алану Тьюрингу и его борьбе с «Энигмой».
В 2001 году вышла картина, которая так и называлась «Энигма», над ней работала блестящая команда английских деятелей культуры: писатель Роберт Харрис, автор одноименного романа; драматург Том Стоппард, превративший этот роман в сценарий; режиссер Майкл Эптед и автор музыки к фильмам о Джеймсе Бонде композитор Джон Барри. А возглавлял это созвездие выступивший в качестве продюсера Мик Джаггер — именно ему, собственно говоря, и принадлежала идея того фильма. Джаггер давно был очарован историей Тьюринга, и в фильме снималась подлинная немецкая машина «Энигма» из его собственной коллекции.
«Игра в имитацию» — тоже экранизация, но не романа, а биографии Тьюринга, написанной историком Эндрю Ходжесом.
Автор фото, studiocanal
Подпись к фото,Для норвежского режиссера Мортена Тилдима «Игра в имитацию» — первый полнометражный фильм на английском языке
Фильм не ставит перед собой задачу скрупулезно проследить жизненную историю ученого. Действие его начинается в 1939 году — со сцены дерзкого собеседования, в результате которого Тьюринг лишь чудом получает место в Блетчли-парк.
Однако ретроспективно мы попадаем в престижную закрытую частную школу, одну из тех английских школ, которые воспитывают известных на весь мир ученых и политиков. Оборотная их сторона — жестокая, удушающая атмосфера, столь блестяще и гротескно воспроизведенная еще в конце 60-х режиссером Линдсеем Андерсоном, намеки на которую мы видим и в «Игре в имитацию».
Поэзия и задавленность любви
Автор фото, studiocanal
Подпись к фото,Главное детище своей жизни — машину, с помощью которой был взломан код «Энигма» — Тьюринг назвал в честь юношеской любви «Кристофер»
Именно в школе пробуждается гомосексуальность Тьюринга. Пробуждается от даже не столько романтического, сколько дружеского чувства к однокласснику Кристоферу Моркому, единственному, кто сочувствует ему и помогает не потерять себя среди издевательств и побоев. Морком умрет в 18 лет от туберкулеза, и чувство к нему Тьюринг пронесет через всю жизнь. Главное изобретение своей жизни — машину, с помощью которой он взломал код «Энигмы», он назвал «Кристофер».
Гомосексуализм Тьюринга – центральный момент в фильме и в осознании личности его героя. Тьюринг по необходимости вынужден был скрывать свою сексуальную ориентацию. В какой-то момент он даже становится объектом шантажа от затесавшегося в группу советского шпиона. Но в то же время он нисколько не стыдится своей природы.
При аресте он совершенно не пытается увиливать и добровольно соглашается написать чистосердечное признание. Пятистраничный текст был написан настолько искренне и с таким достоинством, что даже допрашивавший его полицейский был вынужден признать, что перед ним — «человек чести».
При этом сексуальная сторона жизни Тьюринга совершенно не выпячивается. Во всем фильме нет ни единой сцены, в которой мы видели бы его физические отношения с мужчинами. Подростковое чувство к Моркому проявляется не более, чем взглядом. Кое-кто из критиков усмотрел в такой сдержанности даже чрезмерное для современного кино целомудрие.
«Для меня в фильме более чем достаточно откровенной любви, — отвечает критикам Бенедикт Камбербатч. – И гомосексуальность тут абсолютно ни при чем. Если бы такие сцены могли добавить смысла фильму, обогатить его, мы несомненно пошли бы на это. Для меня в этом не было бы никакой проблемы».
Автор фото, studiocanal
Подпись к фото,Жена Тьюринга (Кира Найтли) была прекрасно осведомлена о гомосексуальности мужа. Для них обоих интеллектуальная, духовная близость была куда важнее физической
«Однако главным для нас, — продолжает актер, — было невидимое: поэзия, тайна, подавленность его сексуальности. Это человек, у которого отобрали право любить — именно в этом трагедия его личности и трагедия фильма».
Жена Тьюринга была прекрасно осведомлена о его сексуальности. Для них обоих интеллектуальная, профессиональная духовная близость была куда важнее физической.
Гений ХХ века
Фильм завершается красноречивым титром: «Его изобретение было далеко от совершенства, но оно породило целую новую область исследований, которая получила название «машины Тьюринга». Сегодня мы называем их «компьютеры».
Шакунтала Деви — Интересные факты о Шакунтала Деви, человек-компьютер
Грядущий биографический фильм, который выйдет 8 мая 2020 года, снятый Ану Менон под названием «Шакунтала Деви», вызвал интерес людей к этой одаренной личности, которой приписывают название «человеческий компьютер». Гений, который мог произвести впечатление на людей с трехлетнего возраста, также является многогранной личностью, хорошо владеющей мотивационными речами и написанием книг разных жанров. Писательница и математик в одном лице, жизнь и достижения Шакунталы Деви вдохновили миллионы людей во всем мире.Вот несколько интересных фактов о Шакунтале Деви, которые вызовут у вас любопытство узнать ее.Рождение и ранние годы жизни Шакунталы Деви
Она родилась в семье индуистских браминов в Бангалоре 4 ноября 1929 года. Когда ей было всего три года, ее отец обнаружил, что она обладает удивительной способностью запоминать числа. Он ушел из цирка, где работал, и устраивал выездные шоу, демонстрируя талант своей дочери в расчетах. В возрасте шести лет Шакунтала Деви доказала свои арифметические способности в Университете Майсура.Она переехала в Лондон со своим отцом в 1944 году.
Признание ее математических талантовУже к пяти годам ее возраста мир понял, что она вундеркинд. Было обнаружено, что она является экспертом в сложной ментальной арифметике. Ее страсть к расширению человеческих возможностей побудила ее разработать концепцию, известную как «динамика разума».
Место в Книге рекордов Гиннеса
Реклама
Ее таланты принесли ей место в Книге рекордов Гиннеса в 1982 году.Ее хвалили как подлинную героиню своего времени, и она могла возглавлять заголовки газет и журналов. Было сказано, что она могла превзойти самые быстрые компьютеры своего времени.
Самая уникальная книга, которую она написала
У нее было мягкое сердце к гомосексуалистам. Она относилась к гомосексуализму в позитивном ключе и написала книгу под названием «Мир гомосексуалистов», которая является первой книгой о гомосексуализме в Индии. Она утверждала, что все люди в разное время проявляют разные сексуальные наклонности и ориентации, и в мире нет ничего, что называется гомосексуальностью или гетеросексуальностью.Она также является автором ряда книг по астрологии и кулинарии.
Ей никогда не нравилось название «Человек-компьютер»В знак признания ее таланта она была провозглашена «Человеком-компьютером» после того, как 5 октября 1950 года она представила свои таланты на канале BBC, организованном Лесли Митчелл. Однако ей никогда не нравилось это название. По ее словам, человеческий разум обладает несравнимо большими возможностями, чем компьютер, и сравнивать человеческий разум с компьютерами неуместно.
Число Шакунтала Деви
Шакунтала Деви приобрела всемирную известность, когда продемонстрировала свою способность умножать два случайных числа из 13 цифр.18 июня 1980 года она смогла мысленно умножить 7 686 369 774 870 × 2 465 099 745 779 и дала правильный ответ 18 947 668 177 995 426 462 773 730 всего за 28 секунд.Причина смерти Шакунтала Деви
Примечательно, что первая женщина-математик в Индии, Шакунтала Деви умерла в Бангалоре 21 апреля 2013 года в возрасте 83 лет из-за сердечных и респираторных заболеваний.
Источники:Shakuntala Devi
https://en.wikipedia.org/wiki/Shakuntala_Devi_(film)
https: // ru.wikipedia.org/wiki/Shakuntala_Devihttps://www.indiatoday.in/education-today/gk-current-affairs/story/shakuntala-devi-the-human-computer-and-author-of-india-s-first-study-on-homosexuality -1600045-2019-09-17
Роль математики в общей учебной программе
Математика является фундаментальной частью человеческого мышления и логики и неотъемлемой частью попыток понять мир и самих себя. Математика обеспечивает эффективный способ развития умственной дисциплины и поощряет логические рассуждения и умственную строгость.Кроме того, математические знания играют решающую роль в понимании содержания других школьных предметов, таких как естественные науки, общественные науки и даже музыка и искусство.
Целью данной TSG является исследование роли математики в общей учебной программе. В связи с широким кругом возможных вопросов, которые могут быть рассмотрены в этой TSG, мы планируем разбить документы и сопутствующие обсуждения по трем ключевым направлениям.
Во-первых, мы задаемся вопросом: почему математика занимает такое важное и уникальное место среди других предметов? То есть каково значение математики в общей школьной программе? В качестве отправной точки мы предлагаем несколько мыслей о том, почему математику следует рассматривать как важный предмет в общей учебной программе.
— Математика носит трансверсальный характер. Если задуматься об истории учебных программ в целом, то математика (геометрия и алгебра) была двумя из семи гуманитарных наук как в греческом, так и в средневековые времена. Эта историческая роль поддерживает представление о том, что математика обеспечивала умственную дисциплину, необходимую для других дисциплин.
— Математическая грамотность является важнейшим атрибутом людей, ведущих более эффективную жизнь в качестве конструктивных, заинтересованных и размышляющих граждан.Математическая грамотность включает в себя базовые вычислительные навыки, количественное мышление, пространственные способности и т. Д.
— Математика применяется в различных областях и дисциплинах, т.е. математические концепции и процедуры используются для решения задач в науке, технике, экономике. (Например, понимание сложных чисел является необходимым условием для изучения многих концепций электроники.) Сложность этих проблем часто требует относительно сложных математических концепций и процедур по сравнению с вышеупомянутой математической грамотностью.
— Математика является частью нашего культурного наследия человечества, и мы обязаны развивать это наследие.
Во-вторых, поскольку математика дает базовые знания и навыки для других школьных предметов, таких как естественные науки, искусство, экономика и т. Д., Вопрос о том, как математика переплетается с другими школьными предметами, заслуживает рассмотрения. В некоторых учебных программах математика предлагается отдельно для поддержки изучения других школьных предметов в качестве «инструментального предмета», а в других учебных программах предлагаются интегрированные курсы, сочетающие математику и другие области.
В-третьих, мы можем захотеть поразмышлять о количестве часов (пропорции часов) и / или курсов, отведенных на математику, по сравнению с другими школьными предметами в учебной программе каждой страны. Помимо этого количественного анализа, необходимо также собрать информацию о качественном описании школьной математики по отношению к другим предметам. Хотя это сравнение не покажет нам всей картины того, почему разные страны придают большое значение математике, сравнение, тем не менее, может вызвать дальнейшие дискуссии.
Скоростная система базовой математики Трахтенберга
Скоростная система базовой математики Трахтенберга — это система мысленной математики, которая частично не требует использования таблиц умножения для умножения. Метод был создан более семидесяти лет назад. Основная идея системы базовой математики Трахтенберга заключается в том, что должен быть более простой способ умножения, деления, возведения чисел в квадрат и нахождения квадратных корней, особенно если вы хотите делать это мысленно.
При решении уравнений недостаточно просто найти ответ, вы также должны доказать себе, что вы нашли правильный ответ. Система Trachtenberg показывает вам инструменты, позволяющие не только быстрее и проще получить ответ, но и то, как вы можете легко проверить свои результаты.
Яков Трахтенберг провел годы в нацистском концентрационном лагере и, чтобы избежать ужасов, он нашел убежище в своей голове, разрабатывая эти методы. Некоторые из методов не новы и используются уже тысячи лет.Вот почему, например, есть некоторое сходство между системой Трахтенберга и ведической математикой. Однако Джекоу считал, что даже эти методы можно упростить. В отличие от ведической математики и других систем, таких как превосходная скоростная математика Билла Хэндли, где метод, который вы выбираете для вычисления ответа, зависит от используемых вами чисел, система Трахтенберга масштабируется от однозначного умножения до умножения на большие числа без изменения метода.
Систему базовой математики Трахтенберга можно преподавать детям, когда они умеют складывать и вычитать.Им не нужно изучать таблицы умножения, прежде чем они смогут умножать с помощью этой системы. Основной метод умножения, преподаваемый в этой системе, идеально подходит для детей и взрослых, которые считают, что они плохо умеют умножать. Правила легко усвоить, и не нужно много практиковаться, чтобы стать профессионалом.
Когда ребенок или взрослый освоится с таблицами умножения, существует прямой метод умножения. При умножении двузначного числа на двузначное число, а также при возведении двузначного числа в квадрат система Трахтенберга использует биномиальное расширение, чтобы сделать вычисления проще и быстрее, чем более традиционный метод умножения.
Как только вы начнете использовать прямой метод умножения, вы обнаружите, что числа, которые вам приходится мысленно складывать, могут стать довольно большими, а итоговые суммы также могут состоять из нескольких цифр при умножении на числа с тремя или более цифрами. Яков Трахтенберг тоже это понимал и снова задавался вопросом, есть ли способ сделать это проще. Был, и это шедевр системы Трахтенберга, это метод умножения на десятки и единицы. Метод десятков и единиц также называется методом двух пальцев, поскольку вы можете использовать два пальца, чтобы отслеживать вычисления по мере продвижения.
При вычислении используется только цифра единицы или цифра десятков из двухзначного результата умножения двух однозначных чисел вместе. Это значительно уменьшает размер чисел, которые вам приходится складывать в голове.
Изучив метод двух пальцев, вы сможете умножить любые два числа и просто записать ответ, когда вы будете мысленно решать уравнение.
Этот сайт посвящен обучению вас системе базовой математики Трахтенберга.Очень краткое введение следует из методов, которые будут рассмотрены. Вы найдете более подробные объяснения всех этих методов на этом сайте.
Простой метод простого умножения
Первая часть системы включает набор правил для умножения любого числа на числа от 0 до 12. Она была спроектирована так, что вам не нужно было знать свои таблицы умножения, поэтому решение проблемы, возможно, не требует никакого умножения!
Например, чтобы умножить 427 на 12, вы следуете правилу «удвойте число и добавьте соседа».
Следующие шаги:
Приготовьтесь начать с того, что поставьте ноль перед множимым и затем подчеркните множимое, так как результат будет ниже.
Начиная справа, удвойте 7. У него нет соседа справа, который можно было бы добавить.
Двигаясь влево к следующему столбцу, удвойте 2 и добавьте 7, его соседа, затем добавьте перенесенную 1.
Двигаясь влево к следующему столбцу, удвойте 4, затем добавьте его соседа, 2, и добавьте перенос.
При переходе к последнему столбцу удвоение нуля по-прежнему равно нулю, поэтому мы игнорируем это и просто добавляем соседа, 4, а затем добавляем перенесенную 1.
Окончательный результат:
Ответ — 5124. Вы можете проделать все это в уме или, в худшем случае, просто записать каждую цифру ответа по мере того, как вы ее вычисляете. Если вам нужен полный пример того, что на самом деле делается, взгляните на умножение на двенадцать.Это очень упрощенный пример для этого введения.
Умножение на числа 0, 1, 2 и 10 настолько просты, что правила умножения на эти числа не новы.
Это была только первая глава книги, следующие главы посвящены умножению скорости прямым методом и методом «двумя пальцами». Эти методы включают другой подход к фактическому умножению, в частности, метод «двух пальцев» был разработан, чтобы максимально упростить вычисления.
Прямое умножение
Метод прямого умножения на самом деле тот же метод, который используется в ведической математике при выполнении «крест-накрест и вертикально», но представлен в одной строке.
Мы рассмотрим небольшой пример и покажем, как обычно решаются уравнения. Версия слева — это то, как уравнения составляются в методе Трахтенберга, вторая — как это показано в ведической математике.
Расчеты:
Первый шаг:
Второй шаг:
, что дает нам
, добавляя перенос из шага 1, который дает нам.
Пишем 2 и несем 1.
Третий шаг:
плюс 1 от переноса дает нам 3
, и ответ — 322.
Этот метод может обрабатывать большие числа, но это означает, что вычисления, которые необходимо сложить вместе, особенно на средних этапах, могут быть довольно сложными. Именно здесь метод «двух пальцев», разработанный Яковом, позволяет вам умножать любые два числа вместе, независимо от их размера, и иметь возможность использовать простое умножение.
«Два пальца» или умножение единиц и десятков
Метод единиц и десятков разбивает умножение на серию однозначных умножений и обрабатывает результаты умножения как двузначный результат:
Поскольку 81 — это максимально возможный результат однозначного умножения, мы знаем, что всегда будут две цифры, если мы поставим ноль перед однозначным результатом. Две цифры представляют собой цифру единиц и цифру десятков.
При объяснении метода мы проводим линию от множителя к множимому с разветвленным концом, чтобы указать, что мы умножим цифру множителя на две цифры множимого.
Для строки, оканчивающейся на U , нас интересует только единичная цифра результата умножения цифры умножителя на цифру множимого, расположенного под линией.
Для наклонной линии, заканчивающейся на T , нас интересует только цифра десятков результата умножения цифры умножителя на цифру множимого, расположенного под наклонной линией.
Опять же, это будет очень краткий пример метода. Вы можете перейти по ссылке, чтобы узнать больше о методе двумя пальцами.Мы рассмотрим тот же пример, который мы использовали выше:
Первый шаг:
, мы игнорируем цифру десятков, 1, и просто используем цифру единиц, 2.
Второй шаг:
Складывая их вместе, получаем
, поэтому мы пишем 2 и несем 1.
Третий шаг:
Мы складываем 2 плюс перенесенный 1 и получаем 3, записываем 3 и получаем ответ 322.
В этом примере метод не передается должным образом, поскольку он становится самостоятельным, когда цифры больше, например 7, 8 и 9. Я действительно хотел, чтобы вы увидели, что эти два метода похожи, а применяемый шаблон одинаков. Если вы сначала изучите прямой метод, тогда будет легче следовать методу двумя пальцами, хотя вам не нужно изучать прямой метод, и вы можете просто сразу перейти к методу двумя пальцами.
Как только вы освоите метод двух пальцев, вычисления станут очень быстрыми, и их очень легко проделать в уме.
Проверка результатов по корням цифр
Jakow также рассмотрел два метода проверки результатов, которые, хотя и были известны в течение сотен лет, в последнее время вышли из употребления с появлением карманных калькуляторов. Методы: изгонять девятки и изгонять одиннадцать.
Очень быстро эти методы включают поиск корня цифры, который в основном представляет собой остаток от деления числа на девять или одиннадцать, в зависимости от того, какой метод вы используете.
Для остатка из девяток корень цифры находится путем сложения всех цифр числа вместе, и если в этой сумме более одной цифры, то складывание цифр до тех пор, пока не останется только одна цифра.
Для одиннадцати остатков существует несколько способов вычисления корня цифры, один из способов — начать с правой цифры и добавить каждую нечетную цифру столбца. Затем вы складываете все четные цифры столбца, а затем вычитаете эту сумму из первой.
Шаг 1: сложите нечетные номера столбцов, выделенные красным
Шаг 2: сложите четные номера столбцов, выделенные синим цветом
Шаг 3: вычтите вторую сумму из первой.
Итак, одиннадцать остатков от 25764 составляют 2
Есть еще несколько соображений, например, что делать, если вторая сумма больше первой. Я не буду здесь рассказывать, что вы можете прочитать больше об остатке одиннадцати или изгнании одиннадцати здесь.
Кроме того, сложение корня из числа добавленных чисел должно совпадать с корнем из числа цифр в ответе. Этот метод также работает для вычитания, умножения и деления, хотя для вычитания лучше проверять его как сложение, а для деления лучше проверять как умножение.
Пример с добавлением остатка девяток:
Сумма 25 цифр:
Сумма 13 цифр:
Сумма 325 цифр:
Для проверки умножаем цифровые суммы множителей:
преобразование 28 в корень из цифры:
Итак, корни двух цифр равны одному, поэтому наш результат должен быть правильным.
Подробнее об остатке девяток или выбрасывании девяток можно прочитать здесь.
Увеличение скорости
В книге представлен метод сложения скорости, в котором вы складываете числа в столбцы, порядок, в котором вы делаете каждый столбец, не важен, поскольку каждый столбец отделен от других.
Что делает его более быстрым, так это одно правило этого метода сложения: вы не считаете больше одиннадцати, как только вы переходите после одиннадцати при суммировании, вы просто вычитаете одиннадцать из общей суммы, ставьте отметку рядом с цифрой, которая вызвала общая сумма должна достигнуть или превысить одиннадцать, и продолжать использовать уменьшенную сумму.
Давайте посмотрим на простой пример:
При суммировании столбца, когда ваша сумма больше 11, вы вычитаете 11 из общей суммы и ставите отметку рядом с числом, которое привело к тому, что общая сумма превысила 11.
В нижней части столбца запишите сумму, которая будет быть максимум 10, это часть вашей текущей суммы.
Ниже промежуточной суммы укажите количество оценок в каждом столбце.
Чтобы получить общую сумму, сложите промежуточную сумму и отметки, начиная с правого столбца и работая слева.
Двигаясь влево ко второму столбцу, складываем L-образную форму. К промежуточному итогу добавьте количество меток в этом столбце, а также количество меток в столбце справа, что дает нам L-образную форму.
Двигаясь влево к третьему столбцу, добавьте количество оценок в этом столбце, а также добавьте количество оценок в столбце справа к промежуточному итогу.
Двигаясь влево к четвертому столбцу, складываем L-образную форму.
В качестве ответа у нас есть сумма.
Длинный дивизион
Яков Трахтенберг также придумал совершенно другой способ деления в длину, который вообще не предполагает никакого деления.
Полностью рабочий пример выглядит так:
Я не буду вдаваться в подробное объяснение здесь, но вы можете перейти в Fast Long Division и узнать больше.
Возведение чисел в квадрат
Яков воспользовался математической техникой, известной как биномиальное разложение, чтобы придумать метод, позволяющий легко находить квадраты любых двух- или трехзначных чисел, а также особый метод для двухзначных чисел, заканчивающихся на 5, а также особый метод. для двузначных чисел, где цифра десятков равна 5.Ведическая математика использует ту же технику.
Примеры конкретных методов:
Возведение в квадрат двузначного числа, заканчивающегося на 5
Любое двузначное число, заканчивающееся на 5, при возведении в квадрат последние две цифры ответа всегда равны 25.
В квадрат 35
Первые одна или две цифры ответа находятся путем умножения первой цифры числа, возводимого в квадрат, на следующую большую цифру.
Мы знаем, что ответ закончится через 25.
Чтобы найти первые цифры ответа, мы берем 3 и умножаем его на 4, следующую большую цифру.
Итак, ответ 1225
Возведение в квадрат двузначного числа, начинающегося с 5
При возведении в квадрат двузначного числа, начинающегося с 5, последние две цифры всегда являются квадратом цифры единиц.
Чтобы получить первые две цифры ответа, мы прибавляем цифру единиц к 25.
Чтобы получить две последние цифры ответа, возводим 6 в квадрат
Чтобы получить первые две цифры ответа, мы добавляем цифру единицы к 25:
Итак, ответ: 3136
Зачем прибавлять к 25? Потому что 5 в квадрате равно 25.
Перейдите по этим ссылкам, чтобы узнать больше о возведении в квадрат двузначных чисел или возведения в квадрат трехзначных чисел. Я предлагаю сначала прочитать о возведении в квадрат двухзначных чисел.
Квадратные корни
Яков Трахтенберг рассказал о поиске квадратных корней из 3–8-значных чисел, но этот метод можно использовать для еще больших чисел. Чтобы увидеть здесь пример того, как найти квадратный корень из трех- или четырехзначных чисел.
Для меня метод вычисления квадратного корня был самым трудным из всех методов в книге, к которому можно было привыкнуть, но ни один из методов, которые я видел для нахождения квадратного корня из большого числа, не является простым.
В заключительную главу книги включены некоторые алгебраические доказательства системы Трахтенберга. Большинство людей не будут интересоваться алгебраическими доказательствами, но они хотят показать, что методы действительно работают и что за ними стоит настоящая математика.
Мои мысли
Эта книга содержит золото, и мне жаль, что меня не учили этим методам в детстве. Я буду учить им своего сына, когда он станет достаточно взрослым.
Методы, которые Яков Трахтенберг извлек из своих многолетних попыток упростить общую основную математику, прекрасны и изобретательны.Хотя он не изобрел некоторые методы, он смог взять это знание
и переработать его дальше, чем это было сделано раньше, и придумал метод двух пальцев и основные правила умножения.
Я могу понять, почему некоторые смеются над его достижениями, делая умножение без умножения, сумасшедший! Тем, кто уже потратил время на запоминание таблиц умножения, это может показаться безумием, но как насчет тех, кто еще не выучил таблицы умножения или тех, кто испытывает трудности с их изучением.Получить другой способ найти ответ, когда вы боретесь с таблицами умножения, намного лучше, чем позволить им потерять уверенность в себе и своих математических способностях.
Я изучал ведическую математику, а также читал некоторые книги Билла Хэндли. Ведическая математика кажется почти мистической из-за учителей, в основном индийских. Методы, используемые Биллом Хэндли, очень похожи на ведическую математику. Если вы заинтересованы в поиске еще одного способа заниматься базовой математикой, я бы порекомендовал книги Билла Хэндли, а не ведическую математику для себя или своих детей.
Почему я должен рекомендовать другой метод изучения математики, если у меня есть целый сайт, посвященный системе Трахтенберга? Ответ таков: не все учатся одинаково, и конечно, есть много людей, для которых метод, которому обучают в школе, достаточно. А что насчет остальных? Может быть, что-то здесь на этом сайте щелкнет для них, или, может быть, это сделают методы Билла.
Почему бы не изучить несколько способов решить одну и ту же математическую задачу? Уверенность в математике дает уверенность и в других областях.Не полагайтесь только на калькулятор, чтобы сделать все свои вычисления и позволить своему мозгу гнить, заставьте свой ум работать, и вы никогда не пожалеете об этом. Математика, которую вы изучаете здесь, — это математика, которую вы можете использовать каждый день.
Проведите некоторое время на этом сайте, осмотритесь, зарегистрируйтесь бесплатно и загрузите рабочие листы для практики. Посмотрите видео, и если у вас есть предложения или вопросы, свяжитесь со мной, и я сделаю все возможное, чтобы вам помочь.
Поделиться:
100 бесплатных вопросов и советов 2021
Числовые тесты мышления используются работодателями для измерения вашей способности выполнять задачи, связанные с числами, и являются одним из основных разделов любого психометрического оценочного теста.
Вопросы варьируются от простых арифметических операций, таких как сложение и вычитание, до более сложных вопросов, где вам нужно интерпретировать числовую информацию, представленную в виде таблиц, диаграмм и графиков.
Тесты на числовые способности популярны среди работодателей, потому что многие рабочие места требуют от вас работы с числами хотя бы часть времени. Если вы подаете заявление о приеме на работу, которая предполагает повседневную работу с цифрами, работодатель будет рассматривать ваши численные способности как ценный показатель вашей эффективности на работе.
В тестах численного мышления вы обычно будете иметь дело с графиками, таблицами, числовыми последовательностями и текстом . Они будут содержать необработанные данные, необходимые для ответа на письменный вопрос, но вам часто придется выполнить несколько операций с этими данными, чтобы получить ответ. Они также могут включать вопросы, в которых математическая задача сформулирована словами, и ваша задача — применить необходимую логику для поиска решения.
На экзаменах для выпускников и руководителей часто ожидается, что вы ответите на вопросов по интерпретации данных .Они имеют форму диаграмм и графиков, которые вам необходимо понять, а затем интерпретировать. Другими словами, вам нужно решить, как получить ответ, а не какие вычисления применить.
Мини-тест числовых способностей
Чтобы помочь вам понять, что включает в себя тест на числовые способности, вот практический тест, с которого вы можете начать:
Чего ожидать от теста на числовые способности
В психометрических тестах регулярно встречаются числовые вопросы двух типов:
- Вопросы о скорости — При неограниченном времени большинство людей, проходящих эти тесты, могут успешно ответить на все вопросы.Однако время, отведенное на выполнение теста, настолько короткое, что даже от самого способного человека не ожидается его завершения. Это означает, что результат зависит от количества правильных ответов, сделанных за относительно короткое время.
- Power test — содержит вопросы разной сложности; ни от кого не ожидается, что он получит правильные ответы на все вопросы, даже при наличии неограниченного времени. На практике для испытаний мощности устанавливается определенное, но достаточное время.
Некоторые более редкие формы числовых тестов не имеют ограничений по времени и / или не имеют отрицательной оценки (неправильные ответы вычитаются из вашей общей оценки, а не просто 0).
В зависимости от провайдера, тесты числового мышления можно сдать дома или в центре оценки; иногда и то и другое — многие организации используют метод борьбы с мошенничеством, который требует от кандидатов лично пройти еще один тест в центре оценки. Если домашний счет и очный счет сильно различаются, то начинают звонить тревожные звонки.
Продолжительность любого теста на числовые способности, который вас попросят пройти, будет зависеть от нескольких факторов, включая количество других тестов, которые вы будете проходить в день.Однако большинство тестов длятся от 30 до 40 минут и содержат от 30 до 40 вопросов.
Вопросы, используемые в тестах на числовые оценки, можно разделить на четыре основных типа:
- Числовые вычисления — Эти вопросы включают основные принципы арифметики, включая сложение, вычитание, умножение, деление, проценты, отношения, дроби и десятичные дроби. Чтобы получить высокие баллы по этим вопросам, вам необходимо быстро и точно рассчитать без использования калькулятора.
- Числовая оценка — Числовая оценка необходима во многих технических работах, когда вам нужно быстро и точно оценить количество материалов и т. Д. Эти вопросы требуют от вас быстрой оценки ответов на простые числовые вопросы. Вы не должны пытаться вычислить ответы; это займет слишком много времени и помешает вам ответить на достаточно вопросов, чтобы получить хорошую оценку.
- Числовое мышление — Эти вопросы проверяют вашу способность к рассуждению, а не способность выполнять вычисления.Другими словами, вам нужно решить, как получить ответ, а не просто сказать, какие вычисления нужно применить. Они всегда включают некоторые вопросы числовой серии, где вам нужно выяснить, какое число или числа отсутствуют в этой серии. Они также включают текстовые вопросы, в которых математическая задача формулируется словами, и ваша задача — применить необходимую логику, чтобы найти ответ.
- Интерпретация данных — Большинство управленческих и надзорных работ требуют от вас интерпретации данных, представленных в диаграммах, таблицах и графиках, для принятия повседневных решений.В этих тестах обычно используются круговые диаграммы, линейные графики, диаграммы рассеяния и таблицы данных, которые необходимо интерпретировать, чтобы ответить на вопросы. Более сложные вопросы могут отображать данные в одном формате (например, в таблице), а часть этих данных — в другом формате (например, в виде круговой диаграммы). Чтобы ответить на вопросы, вы должны иметь возможность логически связать эти два элемента.
Эта статья была разработана таким образом, чтобы вам было легче практиковать те области, в которых вы чувствуете себя наиболее слабыми, что дает вам наибольшую пользу в кратчайшие сроки.Таким образом, каждый тест содержит больше вопросов каждого типа, чем вы получили бы в реальном тесте.
Это также гарантирует, что вы получите максимальное внимание к как можно большему разнообразию стилей и типов вопросов. Важно помнить, что настоящий тест будет содержать вопросы разных типов.
Почему работодатели используют эти тесты?
Психометрические тесты имеют долгую историю исследований. Сильная корреляция между результатами этих тестов и производительностью на рабочем месте привела к тому, что компании во всем мире инвестируют в них как в важную часть процесса найма.
Многим работодателям необходимо знать, что у вас есть прочный фундамент из базовых математических навыков . Эти навыки (расчет процентов, соотношений, дробей, прибыли, выручки и т. Д.) Имеют решающее значение практически в любой сфере бизнеса.
Работодатели используют тесты на числовые способности главным образом по следующим причинам:
- Их проверенный послужной список по показателям производительности на рабочем месте
- Использование математических навыков, необходимых для работы, на которую вы претендуете.
- То, что эти тесты в целом довольно честны
- Они основаны ни на чем, кроме ваших грубых способностей и практики
По этим и другим причинам многие работодатели даже говорят, что они ценят эти тесты на пригодность больше, чем университетские степени.
Рекрутеры компании знают, что их новые сотрудники не обязательно обладают хорошими отраслевыми или специальными знаниями. Вот что приходит с опытом. Ключевым моментом для них является отбор кандидатов, у которых есть основы, позволяющие им адаптироваться к окружающей среде и приобретать необходимые им навыки и знания.
Компании в первую очередь заинтересованы в вашем понимании основ. Они также следят за тем, как быстро вы сможете работать под давлением. Такой вид арифметики должен быть таким, чтобы вы могли делать это быстро и точно, когда это необходимо.
Что усложняет тесты на числовые способности?
Тесты на числовые способности часто являются самым сложным типом проверки способностей для многих кандидатов. Это происходит по нескольким ключевым причинам, которые мы опишем здесь:
Срок
В среднем у вас обычно есть от 45 секунд до 2 минут, чтобы ответить на каждый вопрос.
В нижней части шкалы это действительно сложно. Есть много испытаний, в которых дойти до конца — само по себе подвиг.
Обладать способностями и уверенностью в том, чтобы иметь возможность интерпретировать данные, решать, что нужно сделать, а затем быстро выполнять эти операции, является сложной задачей, поэтому практика очень важна.Мы рекомендуем пакеты числовой практики от JobTestPrep .
Множественные операции
На многие вопросы нет однозначного ответа. Например, вам не нужно просто умножить два числа, чтобы найти решение.
Это навык, о котором часто забывают, который приходит только на практике. Вы можете быть гением в фактическом сложении, умножении, процентах и т. Д., Но вы все равно останетесь позади, если не сможете быстро и точно определить, какие операции вам нужно выполнить и в каком порядке.
Математика
Иногда математические навыки сами по себе могут оказаться трудными, особенно если математика не самая сильная ваша область.
Если учесть две предыдущие трудности — ограничение по времени и понимание того, как ответить на вопрос, — давление ситуации может очень легко помешать хорошей работе.
Различные поставщики тестов численного мышления
Не все численные тесты одинаковы. Хотя все они стремятся проверить одинаковый набор навыков, у каждого создателя тестов будут свои идеи о том, как лучше всего это сделать.
В рамках подготовки, если вы узнаете, какого поставщика услуг тестирования использует компания, к которой вы обращаетесь, вы сможете еще больше сфокусировать свою практику.
Основные провайдеры:
Двумя основными поставщиками тестов являются SHL и Pearson , одни из старейших компаний в отрасли. Их тесты, как правило, устанавливают отраслевой стандарт, и многие поставщики тестов следуют их примеру и вносят лишь относительно незначительные изменения в формат. Если вы сомневаетесь, вы не ошибетесь, практикуя их тесты.
С учетом сказанного, некоторые провайдеры действительно встряхивают.
Например, в Talent Q есть инновационный тест, который адаптируется к вашей работе. Ваши правильные и неправильные ответы помогают проинформировать тест о вашем уровне навыков и соответственно корректировать вопросы. Это позволяет сделать тест гибким и коротким.
cut-e также выделяется из упаковки. С очень короткими тестами, продолжительностью от 5 до 12 минут, его вопросы сосредоточены на более абстрактных математических элементах, а не на графиках и диаграммах.Это может сбить с толку кандидатов, которые привыкли работать с более практичными вопросами.
Выбор поставщика зависит от конкретной роли и отдела. Конечно, вы всегда должны помнить, что компании могут в любой момент сменить поставщика.
Всегда следите за тем, чтобы вы развили необходимые навыки, которые применимы к любому тесту на числовое мышление. Проверяются именно те навыки, а не конкретные знания о конкретном тесте. Большинство работодателей также будут стремиться к тому, чтобы думать на ногах и адаптироваться к изменениям.
Вопросы о численных вычислениях
Численные вычисления вопроса включают математические термины и методы, а также основные принципы арифметики, такие как:
Этот тип теста можно отнести к категории теста скорости и используется для определения вашей базовой математической грамотности. Вам не разрешат пользоваться калькулятором.
Если вы очень плохо разбираетесь в арифметике, попробуйте заново выучить таблицу умножения до 12 и попрактиковаться в умножении, делении и вычислении процентов.Практика может улучшить ваши результаты по всем типам тестов, поэтому попробуйте как можно больше примеров.
Эти вопросы непосредственно применимы ко многим административным и канцелярским должностям, но также могут появляться в качестве компонента выпускных и управленческих тестов.
Скорость, с которой вы можете ответить на эти вопросы, является критическим критерием, так как большинство людей могут получить очень высокий балл, если у них будет неограниченное время для ответа. Таким образом, вы можете рассчитывать на 25–35 вопросов за 20–30 минут.
Простая арифметика
Вы можете значительно улучшить свои результаты, тренируясь в мысленной арифметике, пока вы не станете одновременно быстрым и уверенным. Ваш результат в простых тестах на скорость будет во многом зависеть от вашей способности быстро и точно складывать, вычитать, умножать и делить.
В типичном тесте, состоящем из 60 смешанных вопросов, вам может потребоваться выполнить более 200 отдельных операций умножения и деления. Важно знать свои таблицы умножения (до десятикратной таблицы умножения) и уметь мгновенно ответить на любую операцию.
Ключевое слово здесь — «мгновенный». Большинство людей могут дать мгновенные ответы примерно на 80% этих операций и потратить несколько секунд на то, чтобы подумать об остальном. Эти дополнительные несколько секунд складываются в течение теста, когда ответ на один вопрос может включать три или четыре таких простых действия.
Если вы побрите несколько секунд здесь и там, у вас будет время ответить на четыре или пять дополнительных вопросов в типичном тесте — и это будет иметь большое значение для вашего окончательного результата.
У вас вряд ли возникнут какие-либо проблемы с таблицами умножения на 1, 2, 5 и 10, поэтому вы, вероятно, можете их игнорировать. Возьмите лист бумаги формата A4 и перечислите числа 3, 4, 6, 7, 8, 9 в столбце в левой части страницы и вдоль верхнего поля, как показано:
Работайте по сетке слева направо и сверху вниз, вписывая каждый ответ. Если вы остановитесь хотя бы на секунду, чтобы обдумать ответ, поставьте прочерк и продолжайте.
Не переставай думать.Либо напишите ответ сразу, либо поставьте прочерк. Вы должны выполнить это упражнение менее чем за 40 секунд.
В результате обычно получается лист с несколькими черточками, правильный ответ на который приходит не сразу. Вам нужно будет потратить немного времени на освежение памяти для этих операций — делайте это в течение нескольких дней, тратя пару минут за раз, пока они не станут мгновенными.
Когда вы будете полностью довольны, попробуйте снова сетку — вы сможете правильно заполнить ее менее чем за 40 секунд.
Правила выполнения основных арифметических операций с целыми числами (целыми числами) должны быть вам знакомы, хотя вы можете обнаружить, что некоторые вещи вы забыли. Например:
- Умножение или деление двух целых чисел с разными знаками дает отрицательный результат; например, 5 x –3 = –15
- Умножение или деление двух отрицательных целых чисел дает положительный результат; например, –3 x –3 = 9
Есть несколько советов и приемов, которые помогут вам с умственной арифметикой, которые стоит потратить время на их практику.Все они немного повлияют на вашу общую скорость; если вы сможете освоить несколько из них, и все они просты, то совокупный эффект позволит вам ответить на еще несколько вопросов в отведенное время.
Как вы уже знаете, эти несколько дополнительных оценок могут существенно повлиять на то, как вас будут воспринимать как кандидата на работу.
Вычитание
Рассмотрим сумму: a — b . Есть три подхода к этому виду расчета:
1.Прямой расчет
Когда все цифры «b» меньше, чем цифры «a», расчет может производиться цифра за цифрой.
Например:
Оцените 862 — 41, просто вычтя 1 из 2 в разряде единиц и 4 из 6 в разряде десятков. Это равно 821.
2. Косвенный расчет
Если описанная выше ситуация не применима, проблему иногда можно изменить:
Если только одна цифра в «b» больше, чем соответствующая цифра в «a», уменьшите неправильную цифру в «b» до тех пор, пока она не станет равной соответствующей цифре в «a».
Затем вычтите еще раз, что величина «b» была уменьшена на «a».
Например:
Чтобы вычислить 872–92, превратите задачу в 872–72 = 800. Затем вычтите 20 из 800 = 780.
Если более одной цифры в «b» больше, чем соответствующая цифра в «a», может быть легче найти, сколько нужно добавить к «b», чтобы получить «a».
Например:
Чтобы вычислить 8192–732, мы можем прибавить 8 к 732 (в результате получится 740), затем прибавить 60 (чтобы получить 800), затем 200 (для 1000).
Затем прибавьте 192, чтобы получить 1192, и, наконец, прибавьте 7000, чтобы получить 8192. Наш окончательный ответ — 7460.
3. Прогнозируемый метод заимствования
Этот метод можно использовать для вычитания чисел слева направо, и после небольшой практики он может значительно ускорить мысленное вычитание.
Одно место обрабатывается слева направо.
Пример:
4 075
— 1844
Тысяч:
4 — 1 = 3, посмотрите направо, 075 <844, нужно одолжить.
3 — 1 = 2, скажем, «Две тысячи»
Сотни:
0-8 = отрицательные числа здесь не допускаются
10–8 = 2
75> 44, поэтому не нужно брать в долг, скажем, «двести»
Десятки:
7–4 = 3
5> 4, поэтому не нужно брать в долг, скажем, «тридцать»
Единицы:
5–4 = 1, скажем, «Один»
Это дает 2231 в качестве ответа.
Умножение
Расчет продуктов: a x b
1.Умножение на 2
В этом случае продукт можно рассчитать по цифрам.
Это не совсем так, потому что остаток возможен. Если есть остаток, он всегда равен 1, что значительно упрощает ситуацию. Все-таки произведение надо рассчитывать справа налево:
2 x 167 — это 4 с остатком, затем 2 (то есть 3) с другим остатком, затем 2 (то есть 3).
Таким образом, получаем 334.
2. Умножение на 5
Чтобы умножить число на 5, умножьте это число на 10, а затем разделите на 2.Следующий алгоритм позволяет быстро получить этот результат:
- Сначала добавьте ноль справа от нужного числа
- Затем, начиная с крайней левой цифры, разделите на 2 и добавьте каждый результат в соответствующем порядке, чтобы получить новое число
- Дробь в ответах следует округлить до ближайшего целого числа
Например, если вы намеревались умножить 176 на 5, вы должны сначала добавить ноль к 176, чтобы получить 1760.
Затем разделите 1 на 2, чтобы получить 0.5 округляется до 0
Разделите 7 на 2, чтобы получить 3,5 с округлением в меньшую сторону до 3
Разделите 6 на 2, чтобы получить 3
0 разделить на 2 просто 0
В результате получается номер 0330
.Последний шаг включает прибавление 5 к числу, которое следует за любой отдельной цифрой в этом новом числе, которое было нечетным до деления на два; это лучше понять на примере:
В исходном номере 176 на первом месте стоит 1, что является нечетным. Поэтому мы добавляем 5 к цифре после первого разряда в нашем недавно построенном числе (0330), что составляет 3:
.3 + 5 = 8
Цифра на втором месте 176, 7 тоже нечетная.Следовательно, число-место после соответствующей цифры в построенном числе (0830) также увеличивается на 5.
3 + 5 = 8
Число на третьем месте 176, 6 четное, поэтому окончательное число 0 в нашем ответе не изменилось. Последний ответ — 0880. Крайний левый ноль можно опустить, оставив 880.
Итак, 176 x 5 = 880
3. Умножение на 9
Поскольку 9 = 10 — 1, для умножения на 9 умножьте число на 10, а затем вычтите исходное число из этого результата.
Например, 9 x 27 = 270 — 27 = 243
4. Умножение двух двузначных чисел от 11 до 19
Чтобы легко перемножить двузначные числа от 11 до 19, вы можете использовать этот простой метод сетки:
Рассмотрим расчет 1a x 1b
xx = a + b
yy = a x b
Это можно представить как:
Так, например, вычисление 17 x 16 можно представить как:
Добавление столбцов в сетку дает ответ 272, например:
5.Умножение любых двузначных чисел вместе
Чтобы легко перемножить любые двузначные числа вместе, простой алгоритм выглядит следующим образом:
ab x cd
100 x (a x c) + 10 x (b x c) + 10 x (a x d) + b x d
Например, 23 x 47 можно уменьшить до:
800 (что составляет 2 x 4 x 100)
120 (что составляет 3 x 4 x 10)
140 (что составляет 7 x 2 x 10)
21 (что составляет 7 x 3)
Сумма дает 1081.
Вам нужно будет попрактиковаться в этих методах несколько раз, чтобы стать профессионалом, но они могут значительно сэкономить время, отвечая на вопросы по числовым вычислениям и оценке.
Фракции
Дробь — это число в форме a / b, где «a» и «b» — целые числа.
Буква «a» называется числителем дроби, а буква «b» — знаменателем.
Например, 3/5 — это дробь, числителем которой является «3», а знаменателем — «5». Это можно представить как 3, разделенные на 5.
Если числитель и знаменатель дроби умножить на одно и то же целое число, полученная дробь будет эквивалентной.Если числитель и знаменатель дроби умножить на 5, получится 15/25.
Следовательно, 3/5 = 15/25
1. Сложение, вычитание и сравнение дробей
Чтобы сложить две дроби с одинаковым знаменателем, вы просто складываете числители и оставляете знаменатель неизменным.
3/5 + 1/5 = 4/5
Если знаменатели не совпадают, вам необходимо сделать их такими же, прежде чем выполнять сложение. Для этого нужно получить наименьший общий знаменатель .
В математике наименьший общий знаменатель (сокращенно LCD) — это наименьшее общее кратное знаменателей набора дробей. То есть это наименьшее (ненулевое) число, кратное знаменателям.
Например, ЖК-дисплей 1/2 и 1/4 равен 4, потому что наименьшее общее кратное 2 и 4 равно 4.
Помните, знаменатель говорит о том, на что делится числитель. Любое число, разделенное на 4, будет меньше, чем если бы оно было разделено на 2. Следовательно, 4 является наименьшим общим знаменателем.
Аналогично, ЖК-дисплей 1/2 и 1/3 равен 6, потому что наименьшее (ненулевое) число, кратное 2 и 3, равно 6.
Использование ЖК-дисплея (или любого кратного ему числа) в качестве знаменателя позволяет складывать, вычитать или сравнивать дроби.
Например:
1/2 + 1/4 = 2/4 + 1/4 = 3/4
1/2 — 1/3 = 3/6 — 2/6 = 1/6
1/3 <2/5 с 15.05 <15.06
2. Вычитание дробей
Процесс вычитания дробей, по сути, такой же, как и процесс их сложения — найдите общий знаменатель и замените каждую дробь на эквивалентную дробь с выбранным общим знаменателем.
Полученная дробь будет иметь этот знаменатель, а ее числитель будет результатом вычитания числителей исходных дробей.
Например:
2/3 — 1/2 = 4/6 — 3/6 = 1/6
3. Умножение дробей
Чтобы умножить две дроби, умножьте два числителя и умножьте два знаменателя (знаменатели не обязательно должны быть одинаковыми).
Например:
3/4 x 1/2 = 3/8
4. Умножение дробей на целые числа
Если у вас есть четверть торта, и вы умножите сумму на три, то в итоге вы получите три четверти.Мы можем записать это численно следующим образом:
3 х 1/4 = 3/4
В качестве другого примера предположим, что пять человек работают по три часа из семи часов в день (т. Е. Три седьмых рабочего дня).
В общей сложности они проработают 15 часов (5 х 3 часа каждый) или 15 седьмых дней в день.
Так как семь седьмых дня — это целый день, 14 седьмых — это два дня. Тогда в общей сложности они проработают два дня и одну седьмую дня.
Численно:
5 x 3/7 = 15/7 = 2 1/7
5.Умножение дробей на дроби
Снова рассмотрим пример торта; если у вас есть четверть торта, и вы умножаете количество на треть, вы получаете двенадцатую часть торта.
Другими словами, треть четверти (или треть четверти) равна двенадцатой. Это потому, что каждая четверть делится на три части, а четыре четверти умноженные на три составляют 12 частей (или двенадцатых).
Мы можем записать это численно следующим образом:
1/3 x 1/4 = 1/12
Когда дроби умножаются на дроби, просто умножьте два числителя (верхние числа) и умножьте два знаменателя (нижние числа).
Например:
6. Разделение на дроби
Чтобы разделить одну дробь на другую, инвертируйте дробь, на которую вы делите, и действуйте, как при умножении.
Например:
3/4 ÷ 1/2 = 3/4 x 2/1 = 6/4 = 1½
7. Смешанные числа и неправильные дроби
В приведенном выше примере такое выражение, как 1½, называется смешанным числом . Это означает 1 плюс 1/2.
Например, у вас может быть два целых торта и три четверти другого торта.Целая и дробная части числа пишутся рядом друг с другом:
2 + 3/4 = 2¾
Когда вас просят произвести вычисления со смешанными числами, вам может быть проще преобразовать смешанное число в неправильную дробь.
Неправильная дробь можно рассматривать как еще один способ записать смешанное число; В приведенном выше примере «2¾» представьте, что два целых торта разделены на четыре части. Каждый торт составляет 4/4 от общей суммы, поэтому 4/4 + 4/4 + 3/4 = 11/4 — это еще один способ написать 2¾.
Смешанное число можно преобразовать в неправильную дробь за три шага:
- Умножьте целую часть на знаменатель дробной части
- Добавьте числитель дробной части к этому произведению
- Полученная сумма является числителем новой (неправильной) дроби, а новый знаменатель такой же, как и у смешанного числа
Аналогичным образом неправильную дробь можно преобразовать в смешанное число:
- Разделим числитель на знаменатель
- Частное (без остатка) становится целой частью, а остаток становится числителем дробной части
- Новый знаменатель такой же, как и у исходной неправильной дроби
Например, если вас попросят решить следующее:
7–2
Преобразовать 7 в неправильную дробь: 57/8
Преобразовать 2 ¾ в неправильную дробь: 11/4
Определите ЖК-дисплей: который равен 8
Преобразовать: 11/4 в 22/8
Вычислить: 57/8 — 22/8 = 35/8
Преобразовать: 35/8 в 4⅜
Следовательно, 7⅛ — 2¾ = 4⅜
Десятичные числа
Все числа можно выразить в десятичной форме с основанием 10.Используется десятичная точка, и значение разряда для каждой цифры соответствует степени 10, в зависимости от ее положения относительно десятичной точки.
Например, число 62,437 состоит из 5 цифр, где:
‘6’ — это цифра десятков; значение позиции для «6» — 10
«2» — это цифра «единиц»; значение позиции для «2» — 1
, «4» — это десятая цифра; значение разряда для «4» — 1/10
«3» — это «сотые» цифры; значение разряда для «3» — 1/100
«7» — это тысячная цифра; значение позиции для «7» составляет 1/1000
Следовательно, 82.537 — это краткое написание 60 + 2 + 0,4 + 0,03 + 0,007
Эта система счисления имеет значение для основных операций. Для сложения и вычитания вы всегда должны помнить о выравнивании десятичных знаков:
Например:
126,5 + 68,231 = 194,731 можно записать с выровненными десятичными точками как:
Для умножения десятичных знаков выравнивание десятичных знаков не требуется.
Чтобы определить правильную позицию десятичной точки, вы просто добавляете количество цифр справа от десятичных знаков умножаемых десятичных знаков.
Например:
15,381 x 0,14 = 2,15334
В этом примере у первого числа три десятичных знака, у второго числа два десятичных знака, и, следовательно, ответ должен состоять из пяти десятичных знаков.
Чтобы разделить десятичную дробь на другую, например 62,744 ÷ 1,24, сначала переместите десятичную точку в делителе вправо, пока делитель не станет целым числом, затем переместите десятичную точку в делимом на такое же количество разрядов.
Это дает 6274.4 ÷ 124
Эта процедура определяет правильную позицию десятичной точки в частном (как показано). После этого разделение может продолжаться как обычно.
Преобразование десятичных знаков и дробей
Преобразование заданной десятичной дроби в эквивалентную дробь выполняется просто. Поскольку каждое разрядное значение представляет собой степень десяти, каждое десятичное число можно легко преобразовать в целое число, разделенное на степень десяти.
Например:
84,1 = 841/10
9,17 = 917/100
0.612 = 612/1000
Последний пример можно свести к наименьшим членам, разделив числитель и знаменатель на 4, что является их наибольшим общим множителем.
Наибольший общий делитель двух ненулевых целых чисел — это наибольшее положительное целое число, которое делит оба числа без остатка.
Итак, 612/4 = 153 и 1000/4 = 250
Следовательно, 0,612 = 153/250
Любую дробь можно преобразовать в эквивалентную десятичную дробь. Поскольку дробь a / b означает «a», деленное на «b», мы можем разделить числитель дроби на ее знаменатель, чтобы преобразовать дробь в десятичную дробь.
в процентах
Процент — это способ выражения чисел как дробей от 100, который часто обозначается знаком процента (%).
Например, 45,1% (читается как «сорок пять целых одна десятая процента») равно 0,451.
Проценты используются, чтобы выразить, насколько велико одно количество по отношению к другому количеству. В этом случае первое количество обычно является частью или изменением второго количества.
Например, увеличение на 0,15 доллара по сравнению с ценой в 2,50 доллара — это увеличение на долю 0.15 / 2,50 = 0,06. Таким образом, в процентах это увеличение на 6%.
1. Проценты могут быть относительными
Из-за непоследовательного использования из контекста не всегда ясно, каков процент относительно. Когда говорят о «10% -ном росте» или «10% -ном падении» количества, обычное толкование состоит в том, что это связано с начальным значением этого количества.
Например, 10% -ное увеличение товара, первоначально оцененного в 200 долларов, составляет 20 долларов, что дает новую цену в 220 долларов.Для многих любое другое использование неверно.
Однако в случае процентных ставок обычно используется иное процентное изменение:
Предположим, что начальная процентная ставка задана в виде процента, например, 10%. Допустим, процентная ставка вырастет до 15%. Это можно охарактеризовать как увеличение на 50%, измеряя увеличение относительно начального значения процентной ставки.
Однако на практике многие говорят: «Процентная ставка выросла на 5%».
Чтобы избежать этой путаницы, иногда используется единица «процентные пункты», когда речь идет о разнице в процентах.Итак, в предыдущем примере «Процентная ставка увеличилась на 5 процентных пунктов» было бы недвусмысленным выражением того, что ставка теперь составляет 15%.
С изменениями процентное значение может иметь любое положительное значение. Например, 100% -ный рост является синонимом удвоения; прирост 100%, начиная с 200 единиц, составляет 200 единиц, увеличивая общее количество до 400.
2. Проценты и аннулирование
Распространенная ошибка при использовании процентов — представить, что процентное увеличение отменяется, когда за ним следует такое же процентное уменьшение.
Увеличение на 50% от 100 равно 100 + 50 или 150
Снижение на 50% со 150 составляет 150-75, или 75
Результат меньше 100, с которой мы начали.
Это явление связано с изменением начального значения после первого расчета. В этом примере первое начальное значение — 100, а второе — 150.
В общем, чистый эффект равен: (1 + x) (1 — x) = 1 — x2, то есть чистое уменьшение, пропорциональное квадрату процентного изменения.
В качестве конкретного примера биржевые маклеры пришли к пониманию того, что даже если акция упала на 99%, она, тем не менее, может упасть еще на 99%. Кроме того, если акция растет на большой процент, трейдер все равно теряет всю стоимость акции, если акция впоследствии упадет на 100%, что означает, что она имеет нулевую стоимость.
Практический тест по численным вычислениям
Вопросы по численному мышлению
Тесты численного мышления требуют, чтобы вы интерпретировали некоторую заданную информацию, а затем применили соответствующую логику для ответа на вопросы.Другими словами, вам нужно решить, как получить ответ, а не какие вычисления применить.
Иногда вопросы предназначены для того, чтобы приблизить тип рассуждений, необходимых на рабочем месте.
Самый популярный тип вопросов для числовых рассуждений — это вопросы с числовыми рядами.
Вопросы с числовым обоснованием очень часто используются при отборе выпускников и руководителей. Обычно вы можете ожидать от 15 до 20 вопросов за 20-30 минут.
Численное обоснование становится все более популярным способом оценки кандидатов в процессе отбора вакансий.Многие люди, которые какое-то время не посещали систему образования или не используют математику изо дня в день, испытывают страх перед такими тестами.
Важно помнить, что вам не нужно изучать математику на высоком уровне, чтобы хорошо сдать эти тесты. В первую очередь это тесты на способность рассуждать, а необходимые математические вычисления неизменно просты. Сказав это, вам, возможно, придется разобраться с процентами, соотношениями, пропорциями, дробями и десятичными знаками.
Обычно вам разрешается использовать калькулятор для таких вопросов, и неплохо было бы инвестировать в калькулятор, который может обрабатывать дроби и проценты. Вам также следует попробовать проработать несколько практических работ по числовым вычислениям, чтобы вернуться к размаху этих типов вычислений.
Что такое числовые последовательности
Эти вопросы требуют, чтобы вы нашли недостающее число в последовательности чисел. Этот недостающий номер может быть в начале или в середине, но обычно он находится в конце.
Например:
1. Найдите следующее число в серии
4, 8, 16, 32…
A) 48
B) 64
C) 40
D) 46
2. Найдите недостающий номер в серии
54, 49,…, 39, 34
A) 47
B) 44
C) 45
D) 46
Эти числовые последовательности могут быть довольно простыми, как в приведенных выше примерах.Однако вы часто будете видеть более сложные вопросы, в которых интервалы между числами являются ключом к последовательности.
3. Найдите следующее число в серии
3, 6, 11, 18…
A) 30
B) 22
C) 27
D) 29
4. Найдите следующее число в серии
48, 46, 42, 38…
A) 32
B) 30
C) 33
D) 34
Эти простые числовые последовательности обычно состоят из четырех видимых чисел плюс одно отсутствующее число.Это связано с тем, что разработчику тестов необходимо создать последовательность, в которую может поместиться только одно число.
Необходимость избегать какой-либо двусмысленности означает, что если числовая последовательность основана на более сложном шаблоне, тогда должно быть больше видимых чисел.
Например:
5. Найдите недостающий номер в серии
4, 3, 5, 9, 12, 17,…
A) 32
B) 30
C) 24
D) 26
6.Найдите недостающие числа в серии
5, 6, 7, 8, 10, 11, 14,…,…
A) 19
B) 17
C) 15
D) 16
Ответы:
1. B — числа каждый раз удваиваются
2. B — числа уменьшаются на 5 каждый раз
3. C — интервал, начинающийся с 3, увеличивается каждый раз на 2
4. B — Интервал, начинающийся с 2, увеличивается на 2 и вычитается каждый раз
5.D — Каждое число является суммой предыдущего и цифры 3 слева
6. C, A — Есть две простые чередующиеся последовательности 5, 7, 10, 14, 19 и 6, 8, 11, 15
Чтобы эффективно решать эти вопросы числовой последовательности, вы должны сначала проверить взаимосвязь между самими числами, ища простую арифметическую взаимосвязь. Затем посмотрите на интервалы между числами и посмотрите, есть ли там связь. Если нет, и в частности, если видно более четырех чисел, то могут быть перемежены две числовые последовательности.
Иногда в этих последовательностях можно встретить умножение, деление или степени, но разработчики тестов стараются избегать их, поскольку эти операции вскоре приводят к большим числам, которые трудно вычислить без калькулятора.
Буквы алфавита как числа
Другой тип вопросов последовательности, который появляется в этих тестах, включает замену букв алфавита на числа.
Например:
A = 1, B = 2 и т. Д.
Может показаться странным рассматривать их как вопросы числового мышления, но они работают точно так же, как только вы снова замените их числами.
1. Найдите следующую букву в серии
B, E, H, K,…
i) L
ii) M
iii) N
iv) O
2. Найдите следующую букву в серии
A, Z, B, Y,…
i) C
ii) X
iii) D
iv) Y
Ответы:
1.iii — Две буквы отсутствуют между каждой, поэтому N — следующий
2. i — Есть две чередующиеся последовательности A, B, C и Z, Y, поэтому C — следующий
Поскольку арифметические операции с буквами выполнять нельзя, в этих вопросах меньше места для двусмысленности. Это означает, что чередующиеся последовательности могут использоваться с меньшим количеством видимых букв, чем в вопросах, в которых используются числа.
В этих вопросах «алфавитной последовательности» подразумевается, что последовательность «зацикливается» и начинается снова.Важно понимать это, поскольку обычно об этом не говорится явно — от вас просто ожидается, что вы это узнаете.
Если вы видите более одного из этих вопросов в тесте, почти наверняка стоит потратить время на то, чтобы написать буквы алфавита с их порядковыми номерами под ними.
Затем вы можете рассматривать эти вопросы так же, как вопросы о числовой последовательности. Это может сэкономить много времени и избежать простых ошибок.
Практический тест числового мышления
По крайней мере, в некоторых случаях вы должны отвечать на вопросы в условиях теста .В частности, вам нужно привыкнуть к тому, чтобы рассчитывать время самостоятельно и придерживаться строгих временных рамок.
Если у вас есть 30 минут, чтобы ответить на 30 вопросов, вам нужно убедиться, что вы в среднем не тратите больше минуты на каждый вопрос.
Это можно сделать с помощью секундомера. Каждый раз, когда он достигает минуты (или любого другого среднего времени), сбрасывайте его и двигайтесь дальше. Вернитесь к тем, которые вы не закончили, если у вас будет время в конце. Это поможет вам не волноваться из-за давления самого теста.
Когда вы привыкнете к формату и вопросам, настоящий тест — это просто вопрос сохранения спокойствия и выполнения его.
Всегда полезно широко искать ресурсы, которые помогут вам подготовиться к оценке численного обоснования.
Вот некоторые из наших предложений по дополнительным ресурсам, на которые стоит обратить внимание:
- Приложения — Мы создали приложение для психометрических тестов, доступное как для Apple, так и для Android. Он содержит вопросы, имитирующие вопросы, опубликованные, в частности, SHL, Kenexa, CAPP и Cubiks.Он имеет встроенный таймер, и после этого вы можете проверить решения, чтобы научиться и развиваться.
- Практические онлайн-тесты — Помимо наших собственных тестов на пригодность, WikiJob рекомендует пакеты числовых тестов , доступные в JobTestPrep . JobTestPrep предлагает широкий спектр профессионально разработанных пакетов практических навыков численного мышления, вопросов, тестов и ресурсов. Вопросы структурированы в профессиональном формате, как и настоящие. Практические численные тесты также предлагаются другими провайдерами, такими как Psychometric Success.
Непосредственно перед тестом
Во-первых, убедитесь, что вы выспались, много воды и что-нибудь поесть. Не забудьте взять с собой следующее:
- Калькулятор (если разрешен)
- Секундомер
- Макулатура и карандаш
- Немного воды
Если вы проводите тест дома, найдите тихую уединенную комнату, в которой вы можете посидеть. Убедитесь, что вас не побеспокоят, и проверьте стабильность вашего интернета.
Сделайте глубокий вдох, успокойтесь и начните тест.
Эффективные стратегии при прохождении теста
Если вы хорошо потренировались и подготовились, то, надеюсь, сдача настоящего теста покажется вам знакомой. Просто с чуть большим давлением.
Делайте то, что вы подготовили. Подсчитайте среднее время, которое у вас есть на один вопрос, и используйте секундомер, чтобы успевать вовремя.
Вот несколько вещей, которые следует помнить при прохождении теста:
- Используйте практические вопросы в полной мере. — Часто в начале теста вам будет предложено несколько вопросов-примеров, чтобы вы узнали о формате и сориентировались.Как ставятся вопросы? На что похожи данные? Какие расчеты нужно сделать? Запишите все, что, по вашему мнению, может помочь вам в дальнейшем. Это также будет ваш последний шанс задать какие-либо вопросы до начала теста.
- Внимательно прочтите вопросы — Не позволяйте ограничению времени мешать вам внимательно читать. Это особенно важно, потому что недопонимание часто является причиной того, что вы забываете выполнить конкретный шаг в вычислении или не отвечаете на вопрос.Прочтите каждый вопрос дважды и убедитесь, что вы внимательно прочитали предоставленную информацию.
- Не делайте предположений — Помните, что все, что вам нужно для ответа на вопрос, находится на странице и нигде больше. Если вам посчастливилось вспомнить цифру или факт из своего исследования, который кажется важным, проигнорируйте его. Также используйте эти знания, чтобы ободрить себя. Если ответ найти невозможно, вы точно знаете, что это возможно, основываясь только на том, что написано на странице.
- Используйте процесс исключения — Если вы действительно застряли, посмотрите на некоторые из предложенных вам ответов с несколькими вариантами ответов и работайте в обратном направлении. Посмотрите, есть ли какие-либо ответы, которые определенно выглядят так, как будто они не могут быть ответом, и сначала устраните их.
- Focus — Ключевой навык, который необходимо проверить с помощью числовой оценки, — это ваша способность сканировать данные и оттачивать то, что важно. Вот почему вы должны внимательно прочитать вопрос, чтобы знать, что вам нужно выяснить.Затем внимательно прочтите контекст. Какие данные содержит таблица? Что показывает график? Выясните, какие данные вы можете игнорировать, и заботьтесь только о той информации, которая поможет вам ответить на вопрос.
- Делайте заметки — Держите под рукой свою макулатуру и используйте ее. Жонглировать большим количеством данных и информации в голове может быстро стать непосильной задачей. Избавьте себя от хлопот и запишите факты, которые, по вашему мнению, важны, когда будете работать над вопросом.
- Всегда проверяйте единицы измерения, валюты и базы — Очень распространенная ошибка в числовых тестах — спутать единицы измерения, валюты и т. Д. Иногда вам нужно будет конвертировать между валютами. Использование двух цифр, как если бы они были одной и той же валютой, приведет вас к неправильному ответу. То же самое касается графиков, таблиц и диаграмм. Всегда проверяйте оси, что они представляют и есть ли какие-либо сокращения (например, запись «10» на графике, когда ось объясняет, что это означает «10 миллионов»).Это кажется очевидным, но об этом легко забыть.
- Игнорировать других тестируемых — Если вы проходите тест лично в центре оценивания, скорее всего, вы не останетесь один в комнате. Не позволяйте этому добраться до вас. Другие кандидаты могут вздыхать, ерзать, шуршать бумагой или оглядываться. Это не имеет значения — вы пришли только на свой тест. Некогда отвлекаться, так что держите голову опущенной и сосредоточьтесь на собственном числовом тесте.
Часто задаваемые вопросы
1. Что лучше: закончить тест или сосредоточиться на точности?
В общем, лучше ориентироваться на точность. Даже если вы проходите тест на скорость, точность не менее важна. Для большинства тестов работодатель получит оценку точности, а также ваш исходный балл.
Их больше заинтересует кандидат, который потратил немного больше времени, но был намного точнее, чем кандидат, который участвовал в гонке, но был небрежным.
2. Когда мне следует узнать, как прошел тест?
Какие отзывы вы получаете и когда сильно варьируется от компании к компании.Некоторые не дают вам обратной связи, некоторые — только в случае успеха, некоторые предлагают резюме всем кандидатам.
В зависимости от типа предлагаемой обратной связи это может произойти сразу после завершения теста (автоматическая система обратной связи) или в любое время от нескольких дней до нескольких недель после завершения теста.
Если вы не уверены, получите ли вы обратную связь или когда ее следует получить, просто спросите отдел кадров компании.
3. Могу ли я использовать калькулятор?
При прохождении теста скорости, такого как численная оценка или численное вычисление, вам не разрешается использовать калькулятор.Эти тесты требуют, чтобы вы быстро ответили на простые вопросы по математике и проверили свои умственные арифметические операции.
Обычно вам разрешается использовать калькулятор для числовых расчетов и вопросов интерпретации данных.
Для большинства тестов, проводимых лично в центре оценки, есть калькуляторы, но на всякий случай всегда берите с собой свои. Всегда лучше использовать знакомый калькулятор.
Тип используемого вами калькулятора может помочь или помешать вам в достаточной степени, чтобы повлиять на ваши результаты.В частности, калькулятор, который вы используете, должен:
- Используйте большую клавиатуру, так как это минимизирует ошибки ввода
- Имеют функции процента и памяти
- Не переусердствуйте с несколькими функциями, назначенными каждой клавише
- Отображение нескольких последних цифр и любых связанных операторов (+, -, x, ÷ и т. Д.). Это означает, что вы можете сразу проверить введенные данные, если считаете, что, возможно, допустили ошибку ввода.
- Быть знакомым. То есть вам следовало использовать его на нескольких практических занятиях перед настоящим тестом .
4.Могу ли я использовать свой мобильный телефон во время теста?
Скорее всего, вам не разрешат пройти тест лично, но это все равно не поможет.
Тесты разработаны таким образом, что все, что вам нужно, это ваш калькулятор и ваши собственные числовые навыки. Нет времени искать ответы в Google или на форумах.
5. Я подумываю, чтобы кто-нибудь еще сдал за меня тест
Плохая идея.
Привлечение кого-то другого для прохождения теста может помочь вам пройти онлайн-тесты без надзора и перейти к следующему этапу процесса (при условии, конечно, что этот человек действительно лучше справляется с тестом, чем вы), но работодатели не согласны с этим. это не глупо, и в конечном итоге их не обмануть.
Очень часто на этапе оценивания вас просят пройти еще один набор тестов на способности лично и под наблюдением. Результат этого теста будет сравнен с вашим исходным онлайн-тестом и проанализирован. Если вы обманули, то, скорее всего, на этом этапе вас обнаружат.
И это лишь один из многих методов борьбы с мошенничеством, которые есть у работодателей. Многие из них не разглашаются, потому что, если бы они были, мошенники могли бы искать способы их обойти.
Не рискуйте.Практика — гораздо более эффективная и полезная стратегия.
Последние мысли
Тесты на числовые способности обычно не требуют математических навыков, кроме сложения, вычитания, умножения, деления, соотношений и процентов. Компании в первую очередь заинтересованы в вашем понимании основ. Они спрашивают: «Уверен ли этот человек в работе с числами в целом?».
Однако от вас ожидается, что вы будете выполнять такие арифметические операции быстро и точно.Вы будете испытывать давление как из-за жестких временных рамок, так и из-за важности теста. Хотя эти навыки просты, они должны быть второй натурой. Практикуйте их, пока они не станут такими.
Получить Развивающие математические игры для детей от 4 до 12 лет
Monster Numbers — это обучающая игра для изучения математики: сложение и вычитание, умножение, ряды и числа, математические вычисления и решение задач. Настоящая игра! Более 2300 загрузок во второй день после релиза в США! Подходит для всех возрастов! Дети от 4 до 5 лет найдут соответствующие возрасту игры, соответствующие их уровню зрелости в математике: подсчет монет, логические серии, распознавание чисел, количество и числа ассоциаций, суммы наборов монет.-Дети в возрасте 6 и 7 лет занимаются математическими упражнениями: логические ряды, суммы без перегруппировки, вычитание с монетами и последующее вычитание без перегруппировки. С 8 лет математическая игра состоит из: мысленного арифметического суммирования двузначных чисел, вычитания в уме, умножения, деления и более сложных логических рядов. Самое приятное, что дети будут заниматься математикой, не осознавая этого, из-за большого приключения, которое они переживают с белкой Тобом. Наша белка потерялась в мире Monster Numbers и детей: ДОЛЖНЫ БЫТЬ НА СПАСЕНИЕ !!!! Для этого они должны преодолеть бесчисленные препятствия и попытаться вернуть части космического корабля Тоба.Они могут прыгать, бегать, скользить, летать, стрелять, одновременно выполняя забавные математические вычисления, которые всегда можно адаптировать к вашему уровню. Все время обучения они будут жить в увлекательном приключении, и родителям не о чем будет беспокоиться, потому что Monster Numbers не содержит контента, непригодного для детей. Переведенные на английский, испанский, португальский и русский языки Monster Numbers могут играть мальчики и девочки от 4 лет. Разработано EducaGames, разработано психологами и профессионалами с большим опытом работы в сфере образования.С помощью Monster Numbers ваш ребенок будет изучать математику, даже не осознавая этого. Вы не будете разочарованы !!
Показать большеПознакомьтесь с 20-летним Нилакантом Бхану Пракашем, который выиграл титул «Самый быстрый человеческий калькулятор в мире»
Двадцатилетний Нилаканта Бхану Пракаш из Хайдарабада стал самым быстрым человеком-калькулятором в мире после того, как выиграл первое в истории золото для Индии на чемпионате мира по интеллектуальным вычислениям на Олимпиаде интеллектуального спорта (MSO), недавно прошедшей в Лондоне.
Студент-математик (с отличием) Колледжа Св. Стефана Делийского университета имеет мировые рекорды и 50 рекордов Лимки как самый быстрый калькулятор в мире.
«У меня 4 мировых рекорда и 50 рекордов Limca за то, что я самый быстрый калькулятор в мире. Мой мозг считает быстрее, чем скорость калькулятора. Побить эти рекорды, которые когда-то держали такие маэстро математики, как Скотт Флансбург и Шакунтала Деви, является делом национальной гордости. Я внес свою лепту, чтобы поставить Индию на глобальный уровень математики », — сказал Бхану Пракаш ANI.
«Я выиграл золотую медаль для Индии на MSO в Лондоне 2020, которая проходила 15 августа. Это первая золотая медаль, выигранная Индией. MSO — это самые престижные международные соревнования по играм на развитие умственных способностей и интеллектуального спорта, которые ежегодно проводятся в Лондоне. Это эквивалентно любому другому олимпийскому мероприятию в области физического спорта », — добавил он.
Телангана: 20-летний Нилаканта Бхану Пракаш из Хайдарабада выиграл первое в истории Индии золото на чемпионате мира по интеллектуальным вычислениям на олимпиаде интеллектуальных видов спорта, недавно прошедшей в Лондоне.Он говорит: «У меня 4 мировых рекорда и 50 рекордов Limca как самого быстрого человеческого калькулятора в мире». pic.twitter.com/k17YeYlYnW
— АНИ (@ANI) 24 августа 2020 г.
MSO было проведено виртуально с 30 участниками в возрасте до 57 лет из 13 стран, включая Великобританию, Германию, ОАЭ, Францию, Грецию и Ливан. MSO впервые был проведен в 1998 году.
Бхану Пракаш был на 65 очков впереди ливанского претендента и одного из ОАЭ, занявших третье место.
«Победив 29 участников в возрасте до 57 лет из 13 стран, я выиграл золотую медаль с явным отрывом в 65 очков.Судьи были настолько очарованы моей скоростью, что потребовали от меня дополнительных вычислений, чтобы подтвердить мою точность », — сказал он.
Бхану Пракаш сказал, что его видение состоит в том, чтобы создать лаборатории VISION Math и охватить миллионы детей, чтобы они начали любить математику.
«Мое видение состоит в том, чтобы создать математические лаборатории, охватить миллионы детей, в соответствии с тем, что я называю, чтобы заставить их полюбить математику и арифметические вычисления. Трое из каждых четырех студентов, обучающихся в государственных школах Индии, испытывают трудности с пониманием основ математики.Фобия, вызванная математикой и демотивацией, является второй причиной того, что дети отказываются от посещения сельских школ в Индии », — сказал он.
«Для любой страны, которая может развиваться и процветать во всем мире, умение считать так же важно, как и грамотность. В соответствии с перечисленными правительством целями существует множество программ, которые делают упор на повышение грамотности, но на данный момент нет значимой программы или видения в области повышения математических способностей и навыков счета, которые могли бы вывести нас вперед в глобальной гонке.Наш дальновидный премьер-министр Нарендра Моди должен взять на себя инициативу, поскольку я хочу инициировать и продвигать вперед «ВИДЕНИЕ МАТЕМАТИКИ» Индии. Такой надежный план внесет Индию в мировую карту совершенства и вернет старую индийскую математическую славу », — добавил он.
Шринивас Джонналгадда, отец Бхану Пракаша, сказал, что его сын стал гордиться Индией и имеет видение, как искоренить математическую фобию.
«Бхану оказался гордостью Индии, поскольку он первый индиец, выигравший золотую медаль на Олимпийских играх по интеллектуальному спорту.Он владеет четырьмя мировыми рекордами как самый быстрый человеческий калькулятор в мире, побив рекорды, которые когда-то устанавливались знаменитыми математиками. В свои 20 лет он не только удостоен множества наград, но и обладает видением и миссией искоренения математической фобии, которая является распространенной проблемой по всей стране », — сказал он.
«Золотая олимпийская медаль в умственной математике и интеллектуальном спорте должна быть признана центральным правительством, поскольку она принесла стране такой же успех, как и золотые медали в таких видах спорта, как бокс или бадминтон.Мы считаем, что настало время продвигать математическое образование вперед в тесном сотрудничестве с Фондом Адани, чтобы предоставить детям из малообеспеченных семей лучшее математическое образование, которое обязательно выведет Индию на глобальную карту передового опыта и принесет математике древнеиндийскую математическую славу ». добавил он.
Шринивас Йонналгадда далее сказал, что Бхану Пракаш желает популяризировать тренировку мозга и арифметические упражнения среди детей, чтобы вдохновить их изучать математику и заниматься ею как умственным спортом и вернуть больше золотых медалей в ближайшие дни.
«Бхану Пракаш хочет вызвать чувство удовольствия, когда дети учатся математике, и вся его работа направлена на то, чтобы сделать это реальностью», — сказал он.
мировых рекордов памяти и умственных вычислений
мировых рекордов памяти и умственных вычисленийМировые рекорды по памяти и расчетам
Комментариев? Исправления? Новые записи? Свяжитесь с нами по адресу [email protected]
| Ссылки: Книги памяти, Международный
Ассоциация памяти, Memoriad, Ментальный
Расчет Кубка мира, Память Спортивная база данных в мемо-лагере, Мир
Статистика памяти (Всемирный совет по спорту памяти), Олимпиада интеллектуального спорта, Список рассылки Mental Calculation, Мнемоника, Мемориальный лагерь Книг: Memory Pack от Энди Белла, еще одно воспоминание
рекордсмен БОЛЬШЕ КНИГ … |
| цифр | рекордсмен | год | Связи памяти Pi и Pi: www.pi-world-ranking-list.com worldpifederation.org Pi Links Пи Продиктуйте Книг о Пи: Книга о рекордсмене Пи Раджане Махадеван: Память Поиск по памяти …и если вы достаточно читали о Пи
рассмотрите эту книгу: |
|---|---|---|---|
| 511 | Дэвид Ричард Спенсер (Канада) | ? | |
| 930 | Найджел Ходжес (Великобритания) | 1973 | |
| 1,111 | Фред Грэм (Канада) | 1973 | |
| 1,210 | Тимоти Пирсон (Великобритания) | 1973 | |
| 1 505 | Эдвард К.Берберих (США) | 1974 | |
| 3,025 | Майкл Джон Поултни (Великобритания) | 1974 | |
| 4096 | Саймон Плафф (Канада) | 1975 | |
| 5,050 | Майкл Джон Поултни (Великобритания) | 1977 | |
| 6,350 | Дэвид Санкер (США) | 1978 | |
| 10 000 | Дэвид Санкер (США) | 1978 | |
| 10,625 | Дэвид Фиоре (США) | 1979 | |
| 11 944 | Ганс Эберстарк (Австрия) | 1979 | |
| 15 151 | Хидэаки Томоёри (Япония) | 1979 | |
| 15 186 | Creighton Карвелло (Великобритания) | 1979 | |
| 20 000 | Хидэаки Томоёри (Япония) | 1979 | |
| 20 013 | Creighton Карвелло (Великобритания) | 1980 | |
| 31 811 | Раджан Махадеван (Индия) | 1985 | |
| 40 000 | Хидэаки Томоёри (Япония) | 1987 | |
| 42,195 | Хироюки Гото (Япония) | 1995 | |
| 67,890 | Чао Лу (Китай) | 2005 | |
| 70 000 | Раджвир Мина (Индия) | 2015 | |
Новые рекорды (еще не подтверждены): Акира Харагути
(Япония): 83431 1 июля 2005 г. и 100 000 4 октября 2006 г.
Суреш Кумар Шарма (Индия) 70 030 21 октября 2015 г.
В 1998 году Ип Све
Чой (Малайзия) произнес 60000 цифр числа Пи, используя всего 44 символа.
ошибки.Сим Поханн (Малайзия) произнес 67053 цифры всего из 15 цифр.
ошибки от 14 апреля 1999 г.
Здесь можно найти еще две специальные записи для запоминания числа Пи.
Запоминание случайных чисел
Наибольшее количество цифр, запоминаемых в 2 / из 4 Секунды
Смотреть дополнительно страница с подробностями об этой записи
Наибольшее количество двоичных цифр, запоминаемых в 3 Секунды
Смотреть дополнительно страница с подробностями об этой записи
Максимальное количество двоичных цифр, запоминаемых в одном Протокол
Примечание: Записи со значком «лампочка» были
достигается с помощью лампочек (включенных или выключенных), что делает запись
труднее.
Несколько раз запись за 5 минут (см. Ниже)
превзошел рекорд на одну минуту, поэтому на самом деле рекорд
обладатель 5 минут должен считаться рекордсменом по
тоже одну минуту. Рекорд Итая Авигдора установлен впереди
свидетелей, но не в месте, открытом для широкой публики.
Сообщается новый рекорд (еще не подтвержден): 264 от Джаяшимхи.
Равирала (Индия) и 270 Аравинда Пасупати
(Индия)
Национальный
записи, не упомянутые в приведенной выше таблице:
Индонезия: 216, Доминик Брайан
Хиндарто, 2010
Индия: 132, Нишал Нараянам,
2009
Китай: 100 (в 42.7 секунд),
Цзя Сяося, 2009 г.
Наибольшее количество двоичных цифр, запоминаемых в 5 Протокол
Разговорные номера Скорость одной цифры в секунду)
Разговорные номера Скорость передачи одной цифры каждые 2 секунды)
Три попытки: первая с 100 числами, вторая
с 200 числами и третий с 400 числами (событие сейчас
снято с производства)
Запоминание чисел, мигающая единица
Цифры в секундах на экране
| 259 | Йонас фон Эссен (Швеция) | 2012 |
| 486 | Цогбадрах Сайханбаяр (Монголия) | 2016 |
Запоминание записанных чисел (1 Минуты)
ошибки не допускаются
Запоминание записанных чисел (100 Цифры)
ошибки не допускаются
Запоминание записанных чисел (5 Протокол)
Участники запоминают номер, записывая его.Нет ошибки в каждая строка из 40 цифр приносит 40 баллов. Однако одна ошибка снижает оценку в этой строке до 20, вторая ошибка снижает оценка для этой строки равна нулю.
Запоминание записанных чисел
(15 минут)
Участники запоминают номер, записывая его. Нет ошибки в каждая строка из 40 цифр приносит 40 баллов. Однако одна ошибка уменьшает количество очков в этой строке до 20, вторая ошибка снижает оценка для этой строки равна нулю.
Ян Форман (Дания)
запомнил 760 цифр на чемпионате мира по запоминанию 2004 года.
это мероприятие немного отличалось от других конкурсов памяти.
Запоминание записанных чисел (30 минут)
Случайные числа представлены рядами по 40 цифр. Подсчет очков в таблице по строкам: по одному баллу за каждую цифру. Однако одна ошибка уменьшает количество очков в этой строке до 20, вторая ошибка снижает оценка для этой строки равна нулю.
Запоминание записанных чисел (1 Час)
Случайные числа представлены в 25 строках по 40 цифр. Подсчет очков в таблице по строкам: по одному баллу за каждую цифру. Однако одна ошибка уменьшает количество очков в этой строке до 20, вторая ошибка снижает оценка для этой строки равна нулю.
Запоминание двоичных чисел (30 Протокол)
Случайные двоичные числа представлены строками по 30 цифр.Подсчет очков табулируется по строкам: по одному баллу за каждую цифру. Однако один ошибка снижает счет в этой строке до 20, вторая ошибка уменьшает оценку для этой строки до нуля.
Запоминание слов / текста
Самый впечатляющий способ запоминания слов — запоминание 23200 слова в течение 72 часов — сообщил Рамн Кампайо (Испания). К сожалению, письменной документации нет о его записях, так что их нельзя считать «официальными» записи для этого списка.
Запоминание ранее неопубликованного текста
(15 минут)
(Эта категория больше не проводится на конкурсах памяти.)
| 345 баллов | Астрид Плессл (Австрия) | 2003 |
Запоминание случайных слов (5 минут)
| 80 | Корнелия Бедди (Германия) | 2006 |
| 109 | Кэти Кермод (Великобритания) | 2009 |
| 119 | Борис-Николай Конрад (Германия) | 2013 |
| 124 | Саймон Рейнхард (Германия) Йоханнес Маллоу (Германия) | 2013 2015 |
| 125 | Саймон Рейнхард (Германия) | 2015 |
| 134 | Саймон Рейнхард (Германия) | 2016 |
| 140 | Йоханнес Мальва (Германия) | 2017 |
| 145 | Янджа Винтерсоул (Монголия) | 2018 |
Запоминание случайных слов (15 минут)
Случайные слова представлены в столбцах по 25 слов.Подсчет очков таблица по столбцам: по одному баллу за каждое слово. Однако одна ошибка снижает оценку в этом столбце вдвое, вторая ошибка снижает оценку этого столбца до нуля.
Запоминание игральных карт
Наибольшее количество запоминаемых карточек (перемешанные пачки)
Рекорд по наибольшему количеству колод из 52 карт. перетасовывались, запоминали и вспоминали. Участник разрешено просматривать карты только один раз.
Правила:
Два независимых свидетеля / наблюдателя, лица с некоторым авторитетом в сообществе, должен присутствовать на протяжении всей попытки. Если вызывается неправильная карта, и это немедленно исправляется и самопроизвольно без подсказки, то это не будет считаться ошибка. Максимальное допустимое количество ошибок — половина одной. процент от общего количества задействованных карт, округленный до ближайшее целое число.
Время, затрачиваемое на запоминание карточек и их повторение, должно быть записаны, но не являются существенными требованиями записи.
| История этого запись, написанная Домиником О’Брайеном, можно прочитать ЗДЕСЬ. |
10 минут запоминания нескольких Карт
Участникам дается 10 минут на то, чтобы запомнить как можно больше из 12 пачек. карт (по 52 карты) как можно. Никаких ошибок в пачке карты набирают 52 балла, одна ошибка дает 26 баллов и более одна ошибка дает ноль баллов.
(c) достигнуто на соревновании с использованием компьютеров вместо реальных игральные карты30 минут запоминания нескольких Карт
1 час запоминания нескольких пакетов Карточки
Участникам дается час на то, чтобы запомнить как можно больше из 12 упаковок карты (по 52 карты) как можно.В колоде карт нет ошибок набирает 52 балла, одна ошибка дает 26 баллов и более одной ошибка получает ноль баллов.
Рекорд скорости: единичная упаковка («Скорость
Карты »)
Рекорд по самому быстрому времени, чтобы запомнить одну пачку 52 карты перетасованы без ошибок.
Используя программное обеспечение Memoriad, Александр Маллен запомнил колоду
карты за 17,69 секунды на Memoriad 2016 в Лас-Вегасе.
Speed Record две деки
Основные правила такие же, как и для одной колоды. Каждая упаковка следует тасовать отдельно, колоды НЕ смешивать. В на каждом этапе нужно переворачивать две карты вместе — одну из первая колода, вторая из другой колоды. Каждый раз участники могут видеть две карточки.
Записи
| 3:37 мин. | Доминик О’Брайен (Великобритания) | 2001 |
Запоминание имен и лиц (5 минут)
Лица представлены конкурсантам в определенном порядке с
соответствующие имена внизу.Затем они представлены в новом
заказ без имен. Участники конкурса отмечают имена на новых листах. Один
балл начисляется за каждое правильное имя, по одному баллу за каждое
фамилия.
ПРИМЕЧАНИЕ: Рекорды до 2015 года были достигнуты в конкурсах, где только
необходимо запоминать типичные «национальные» имена.
Запоминание имен и лиц (15 минут)
Лица представлены конкурсантам в определенном порядке с соответствующие имена внизу.Затем они представлены в новом заказ без имен. Участники конкурса отмечают имена на новых листах. Один балл начисляется за каждое правильное имя, по одному баллу за каждое фамилия.
Примечание: Рекорд по международным именам и лицам —
категория, которая сейчас используется в соревнованиях на запоминание — это 200 баллов.
Кэти Кермод (Великобритания).
Запоминание (вымышленных) исторических дат (5 минут)
Запоминание абстрактных изображений (15 минут)
Игра в игры по памяти с завязанными глазами
Шахматы
претензий в этой категории были поставлены под сомнение слухами о том, что
мастер записал игры или это большое количество
например, оппоненты согласились уйти в отставку после нескольких номинальных ходов.Следующая таблица содержит записи, которые были приняты
шахматное сообщество.
Обширную информацию о шахматах с завязанными глазами можно найти в книга «С завязанными глазами» Шахматы »Элиота Херста и Джона Кнота и веб-сайта www.blindfoldchess.net.
| игры | игрок | год | результат |
| 1 1 | Саид бин Джубайр Йозеф Челеби (Греция) | ~ 690 970 | |
| 2 | Буззекка (Сарацин) | 1265 | |
| 3 3 3 3 3 3 | Аль-Джами Джованни Джироламо Саккери (Генуя) Франсуа Андр Даникан Филидор (Франция) Лионель Кизерцки (Франция) Уильям Льюис (Великобритания) Луи Шарль де ла Бурдонне (Франция) | 1331 1667 1783 1846 | |
| 4 4 | Лионель Кизерцки (Франция) Луи Паульсен (Германия) | 1851 1857 | + 3 = 0–1 + 2 = 1–1 |
| 5 | Луи Паульсен (Германия) | 1857 | + 4 = 1-0 |
| 7 | Луи Паульсен (Германия) | 1858 | 7 = 0-0 |
| 8 | Луи Паульсен (Германия) | 1858 | |
| 10 | Луи Паульсен (Германия) | 1858 | + 9 = 1-0 |
| 15 15 | Луи Паульсен (Германия) (оспаривается) Джозеф Блэкберн (Великобритания) | 1859 1876 | |
| 16 16 | Йоханнес Херманн Цукерторт (Польша) Гарри Нельсон Пиллсбери (США) | 1876 1900 | + 12 = 3–1 + 11 = 4–1 |
| 17 | Гарри Нельсон Пиллсбери (США) | 1900 | + 10 = 5-2 |
| 20 | Гарри Нельсон Пиллсбери (США) | 1897 | + 14 = 5–1 |
| 21 | Гарри Нельсон Пиллсбери (США) | 1902 | + 3 = 11-7 (очень сильные противники) |
| 22 | Гарри Нельсон Пиллсбери (США) | 1902 | + 17 = 4–1 |
| 24 | Рихард Рти (Чехословакия) | 1919 | + 12 = 9-3 |
| 25 | Дьюла Брейер (Венгрия) | 1921 | + 15 = 7-3 |
| 26 | Александр Алехин (Франция) | 1924 | + 16 = 5-5 (очень сильные противники) |
| 28 | Александр Алехин (Франция) | 1925 | + 22 = 3-3 |
| 29 | Рихард Рти (Чехословакия) | 1925 | + 20 = 7-2 |
| 30 | Георгий Колтановски (Бельгия) | 1931 | + 20 = 10-0 |
| 32 | Александр Алехин (Франция) | 1933 | + 19-9 = 4 |
| 34 | Георгий Колтановски (Бельгия) | 1937 | + 24 = 10-0 |
| 40 | Мигель Найдорф (Аргентина) | 1943 | + 36 = 1-3 |
| 45 | Мигель Найдорф (Аргентина) | 1947 | + 39 = 4-2 |
| 46 | Marc Lang (Германия) ПОДРОБНЕЕ | 2011 | + 25 = 19-2 |
Черновики
| игры | игрок | год | результат |
| 2 | Бен Спрингер (Нидерланды) | 1926 | + 1 = 1-0 |
| 5 | Пит Роозенбург (Нидерланды) | 1950 | |
| 8 | Вим Хейсман (Нидерланды) | 1955 | + 5 = 1-2 |
| 10 | Тон Сиджбрандс (Нидерланды) | 1982 | + 9 = 1–1 |
| 12 | Тон Сиджбрандс (Нидерланды) | 1986 | + 11 = 1-0 |
| 14 | Тон Сиджбрандс (Нидерланды) | 1987 | + 12 = 1–1 |
| 15 | Тон Сиджбрандс (Нидерланды) | 1991 | + 13 = 2-0 |
| 18 | Тон Сиджбрандс (Нидерланды) | 1993 | + 14 = 4-0 |
| 20 | Тон Сиджбрандс (Нидерланды) | 1999 | + 17 = 3-0 |
| 22 | Тон Сиджбрандс (Нидерланды) | 2002 | + 17 = 5-0 |
| 24 | Ton Sijbrands (Нидерланды) ВИДЕО | 2004 | + 20 = 4-0 |
| 25 | Тон Сиджбрандс (Нидерланды) | 2007 | + 21 = 4-0 |
| 27 | Эрно Просман (Нидерланды) | 2008 | + 15 = 8-4 |
| 28 | Ton Sijbrands (Нидерланды) | 2009 | + 18 = 7-3 |
| 30 | Эрно Просман (Нидерланды) ВИДЕО | 2012 | + 17 = 8-5 |
| 32 | Ton Sijbrands (Нидерланды) ВИДЕО | 2014 | + 14 = 8-0 |
В 1947 году Ньюэлл У.Бэнкс (США) играл вслепую по 4 часа в день в течение 45 дней подряд, выиграв 1331 игру, проведя вничью 54 и проиграл только две, играя одновременно в шести играх.
Кубик Рубика
см. Дополнительную страницу с подробнее об этой записи
Психологический расчет: добавление
Сложение 100 однозначных чисел номера
Правила:
Общие правила для
расчетные записи применяются.
- Это рекорд самого быстрого времени, которое может добавить человек. вместе 100 однозначных чисел.
- Рекорд — это проверка прямого умственного расчета. Калькулятор должен производить расчет в его голове. без посторонней помощи и без использования счетные машины, компьютеры и т. д., а также калькулятор запишите числа.
- 100 чисел (0-9), которые нужно сложить, должны быть случайным образом выбирается компьютером непосредственно перед расчетом и должно отображаться калькулятору на экране компьютера, доска, экран или аналогичный.В идеале числа должны быть представлены на экране рядами, например, по пять или десять цифры.
- Калькулятор должен видеть все числа одновременно — числа могут не появляться один за другим на экране и т. д. для калькулятор.
- Калькулятор должен записать ответ на расчет.
- Отсчет времени начинается, когда 100 чисел становятся видимыми для участника и заканчивается по окончании написания ответа.
- В некоторых случаях калькулятор может продиктовать ответ — тогда отсчет времени заканчивается, когда калькулятор заканчивает надиктовывать ответ.
- Следует использовать два секундомера: эти секундомеры записывают в минутах, секундах и десятых долях секунды а не сотые доли часа. В конце попытки время следует рассматривать как среднее для двух часов.
| 32.57 с | Р. Х. Фрост (Великобритания) | 1977 |
| 19,23 с | Альберто Кото (Испания) | 1999 |
| 14,71 с * | Рамон Абелла Вилья (Испания) | 2019 |
Результат от Рамона Абелла Вилла получила в среднем три правильных результата подряд. расчеты (завершены в 14.97 сек, 14,88 сек и 14,28 сек).
Сложение десяти 10-значных числа
(10 заданий на правильное сложение десяти десятизначных чисел)Общие правила для расчетные записи применяются.
| Альберто Кото (Испания) | 5:50 мин. | 30 октября 2004 г. при ментальном расчете Кубок мира в Аннаберг-Бухгольц (Германия) |
| Хорхе Артуро Мендоса Уэртас
(Перу) | 5:36 мин. | 27 апреля 2005 г. в Национальном
Университет Перу |
| Альберто Кото (Испания) | 4:35 мин. | 1 июля 2008 г. при мысленном вычислении
Чемпионат мира по футболу в Лейпцигском университете (Германия) |
| Альберто Кото (Испания) | 4:26 мин. | 1 июля 2008 г. при мысленном вычислении Чемпионат мира по футболу в Лейпцигском университете (Германия) |
| Рамон Абелла Вилла (Испания) | 4:22.6 мин. | 21 июня 2009 г.
Impossibility Challenger Games в Дахау (Германия) |
| Рамон Абелла Вилла (Испания) | 4: 02,9 мин. | 21 июня 2009 г. Impossibility Challenger Games в Дахау (Германия) |
| Альберто Кото (Испания) | 3:42 мин. | 6 июня 2010 г. при мысленном вычислении
Чемпионат мира по футболу в Магдебурге (Германия) |
| Марк Хорнет Санс (Испания) | 3:19.4 мин. | 23 сентября 2010 г.
Математический факультет Университета Валенсии (Испания) |
| Наофуми Огасавара (Япония) | 3:11 мин. | 30 сентября 2012 г. в Mental Calculation
Чемпионат мира по футболу в Гиене (Германия) |
| Акшита Шайлеш Шах (Индия) | 3: 06,9 мин. | 23 ноября 2012 г., Мемориад 2012 в отеле Belconti Resort в Анталии (Турция) |
| Грант Ракеш Таккар (Индия) | 3:06.3 мин. | 23 ноября 2012 г., Мемориад 2012 в Belconti Resort Hotel в Анталии (Турция) |
| Наофуми Огасавара (Япония) | 2: 51,1 мин. | 24 ноября 2012 г., Мемориад 2012 в Belconti Resort Hotel в Анталии (Турция) |
| Чонхи Ли (Южная Корея) | 1:40 мин. | 31 июля 2014 г. в средней школе Дуайта Морроу в г.
Энглвуд, Нью-Джерси (США) |
Существует также страница подробной статистики с мировыми рейтингами и национальные рекорды.
Психологический расчет: Умножение Иоганн Мартин Захариас Дасе (Германия, 1824-1861)
умножил два 20-значных числа за 6 минут и два 100
цифры в 8 3/4 дома в 1861 году. В 1980 году, Шакунтала Сообщается, что Деви (Индия) умножила два 13-значные числа за 28 сек. Эта запись была принята Книгу рекордов Гиннеса, но позже добавили комментарий «Некоторые специалисты по вычислению вундеркиндов отказываются верить вышесказанному — в основном на том основании, что он намного превосходит вычисления любого другой бдительный вундеркинд.« Книга рекордов Лимки (Индия) принимает этот рекорд как а также «Книгу ментальных записей Бузана», в которой говорится: «Мы со всем уважением отмечаем, что миссис Деви неоднократно наблюдался, появлялся на многочисленных прямые телешоу, выполняющие «новые» расчеты на основе на работы различных профессоров математики, и последовательно выполняется на указанном в ней уровне рекордная производительность.Мы поддерживаем миссис Деви в ней природное совершенство, и надеемся, что исследователи все больше осознают, что их изумление и веселье не должно заключаться в выдающемся превосходстве любого человеческого умственная работоспособность, но в редких случаях подобные спектаклей ». Примечание: один из множителей, которые ей нужно было умножить, закончился 0, так что на самом деле она умножила 12-значное число на 13-значное число. Умножение двух 5- или 8-значных цифр Номера Правила:
Существует также страница подробной статистики с мировыми рейтингами и национальные рекорды. | Книги о ментальных вычислениях: Ментальный
Справочник калькулятора, составленный чемпионами мира
Роберт Фонтан и Ян ван Конингсвельд ЗАКАЗАТЬ с amazon.com Счет мертвых
— Расчет без приборов ЗАКАЗАТЬ с amazon.com Как записаться рассчитать быстро ЗАКАЗАТЬ от амазонки.com БОЛЬШЕ КНИГ … | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Мысленный расчет: извлечение корней
Вычисление квадратного корня шестизначного числа
13-й корень из 100-значного числа
23-й корень из 200-значного числа
см. Дополнительную страницу с подробностями об этих
записи
Мысленный расчет: календарь по памяти
20 дат из одного века
Все даты из одного года
Большинство дат с 1600 по 2100 в течение одной минуты
см. Дополнительную страницу с подробной информацией о
эти записи
Мысленное вычисление: решение линейного уравнения Системы
Селук Сонер Акгл (Турция) решил десять систем линейных уравнений (каждая с тремя уравнениями и тремя переменными, каждая из которых имеет ровно одно целочисленное решение) в 10:21.77 минут 20 октября 2010 г. 9-й математический симпозиум в Техническом университете Карадениз, Турция.Мысленный расчет: факторизация чисел
Необходимо найти все простые множители для 20 случайных пятизначных чисел. (которые не являются простыми числами)
Учебник Виллема по поиску множителей больших чисел может быть нашел здесь.