Ментальная арифметика видео уроки бесплатно с нуля
Заинтересовала ментальная математика? Но не знаете, с чего начать? Специально для знакомства — наши лаконичные видеоуроки, которые вы можете посмотреть бесплатно в любое время!
Они подойдут родителям, которые планируют начать самостоятельное обучение детей счету. Полезны будут и для детей, дошкольников и младших школьников. А также всех-всех, кто хочет понять, как научиться считать быстро, с нуля, решать примеры и не бояться математики.
Посмотрите все уроки — это не займет много времени!
Подарите вашим детям увлекательный мир овладения счетом и решения задач!
Урок 1. Знакомимся с Абакусом
Узнайте, что такое ментальная арифметика, счеты Абакус, откуда они пошли и из каких элементов состоят.
Урок 2.
 Начинаем считать
Начинаем считатьПосмотрите это видео и через 1 минуту вы узнаете, как выполняется счет на Абакусе, как выставлять единицы, десятки и сотни.
Урок 3. Какими пальцами набирать
Это короткое видео расскажет, какими пальцами удобно работать на счетах и набирать цифры, напомнит принцип подсчета.
Урок 4. Учимся вычитать
Узнайте, как быстро решать примеры на вычитание, как набирать их на счетах и получать верный результат.
Урок 5.
 Веселая ментальная карта
Веселая ментальная картаСейчас вы увидите, что такое ментальная карта и как она используется в домашних условиях, при занятиях с ребенком.
Урок 6. Легко складываем и вычитаем большие числа
Этот видео-урок научит вашего ребенка работать с большими числами, уверенно складывать и вычитать, быстро решать разные примеры.
Урок 7. На чем потренироваться
Узнайте, какое приложение вы можете установить на планшет или телефон для тренировок в решении задач, как им пользоваться.
Урок 8.
 Быстрое руководство по Know Abacus
Быстрое руководство по Know AbacusПознакомьтесь с приложением для начинающих и продолжающих освоение ментальной математики!
Урок 9. Легкое понимание состава числа 10
Веселое, игровое мини-видео научит вашего ребенка составу чисел, визуально закрепит в его памяти составляющие Десятки.
Урок 10. Уровни ментальной арифметики
Узнайте, что это такое и какая сложность уровней, какие примеры и задания туда входят.
Ментальная математика в домашних условиях
Ментальная арифметика
Ментальная арифметика – это уникальная методика развития умственных способностей детей от 4 до 16 лет, основанная на системе устного счета. Обучаясь этой методике ребенок может решить любые арифметические задачи за несколько секунд (сложение, вычитание, умножение, деление, вычисление квадратного корня числа) в уме быстрее, чем с помощью калькулятора.
Обучаясь этой методике ребенок может решить любые арифметические задачи за несколько секунд (сложение, вычитание, умножение, деление, вычисление квадратного корня числа) в уме быстрее, чем с помощью калькулятора.
В чем же отличие нашей методики обучения ментальной арифметике от других методик?
- Наличие методических пособий для инструкторов, содержащих подробно расписанные планы для каждого урока.
- Каждый урок дети проходят новую тему, поэтому исключено нахождение в одной группе детей с разными уровнями занятий и владений техники ментальной арифметики.
- Каждая тема объясняется в 6 этапов, а с 3-го уровня — в семь этапов. При этом отрабатываются все каналы восприятия информации у ребенка. Т.е. только одна новая тема отрабатывается в течение 45 минут. Только убедившись, что каждый ребенок на 100% понял и отработал новый материал, ему дается домашнее задание для закрепления полученных знаний и навыков дома.
- Методика прописана детально и глубоко. При работе над новой темой, обязательно включается материал для повтора и закрепления ранее пройденных тем, чем достигаются прочные знания и навыки.
 Поэтому исключается добавление новых учащихся в группу на любом этапе обучения и с любым уровнем знаний.
Поэтому исключается добавление новых учащихся в группу на любом этапе обучения и с любым уровнем знаний. - Тщательно и детально разработанные книги для обучения. На каждую новую тему отводится не менее 8 страниц. На каждой странице по 4 строчки, по 10 примеров. Что больше обычно предлагаемого другими школами в 2-3 раза.
- Учитывая наш менталитет, уже с третьего урока в наших школах дети начинают считать ментально. Как только ребенок отработает полученные навыки на абакусе, ему предлагается сделать это уже ментально, используя воображение, сначала на легких примерах без формул, затем постепенно счет усложняется. Это очень сильно мотивирует детей к обучению, т.к. уже с первых шагов в изучении ментальной арифметики они видят результаты, хорошо усвоенный материал и отработанные навыки делают этот процесс максимально несложным. Они пробуют, у них получается и дети приобретают чувство уверенности в себе, в своих способностях и знаниях. Другие методики, как правило, в течение года изучают все формулы на абакусе, и только через год начинают пытаться считать ментально.

- Уникальный образовательный онлайн портал для учеников, созданный специально для методики ISMA. Дети тренируются на портале ежедневно. Работа портала настроена таким образом, что инструктор контролирует регулярность и правильность выполнения домашнего задания, отслеживает статистику и анализирует развитие ребенка. Если ребенок не тренируется в портале, то это сразу видно, падает его рейтинг. Это является мощным инструментом самоконтроля и мотивации для ребенка, контроля со стороны не только инструктора, но так же и родителей, которые в любой момент могут зайти на портал и проследить динамику развития ребенка. Кроме арифметических заданий, на портале так же есть задания на развитие логики, внимания, фотографической памяти. Данные тренировки очень важны для отработки и закрепления навыков.
- Дети решают задания с формулами на сложение и вычитание параллельно. Обычные зарубежные методики предлагают задания в основном на сложение. Вычитание они проходят отдельными формулами.
 Методика ISMA так же учит детей считать отрицательные числа, десятичные дроби, корень квадратный, корень кубический , проценты. Вести подсчеты в денежном выражении, в выражении массы и других мерах.
Методика ISMA так же учит детей считать отрицательные числа, десятичные дроби, корень квадратный, корень кубический , проценты. Вести подсчеты в денежном выражении, в выражении массы и других мерах. - Уникальность методики заключается еще в том, что это наш, казахстанский продукт, который успешно работает в течение 4 лет не только на рынке Казахстана, но и в странах ближнего и дальнего зарубежья. Кроме того, методика постоянно совершенствуется и развивается — в этом ее преимущество перед приобретенными за рубежом, т.к. законодательно невозможно вносить изменения, улучшения в шаблон приобретенной чужой методики, даже если она не совсем подходит для нашего менталитета. Это очень важный аспект. Даже на небольшом примере: во многих методиках число 5 250 пишется, как 5,250. Школы в данном случае не могут отойти от регламентов приобретенной методики. В нашей же системе образования запятая после числа пять означает, что далее идут сотые. И число читается, как пять целых двести пятьдесят сотых.
 У детей возникает своего рода конфликт восприятия числа, т.к. школа требует одну систему, в школе ментальной арифметики — другую систему. Отсюда возникает недовольство и негатив у школьных учителей в отношении ментальной арифметики.
У детей возникает своего рода конфликт восприятия числа, т.к. школа требует одну систему, в школе ментальной арифметики — другую систему. Отсюда возникает недовольство и негатив у школьных учителей в отношении ментальной арифметики.
Обучение ментальной арифметике по методике ISMA учитывает требования школы, особенности менталитета и психологии наших детей, что позволяет добиться отличных результатов не только в обучении ментальной арифметике, но существенно повысить общую успеваемость в школе.
Кроме того, знания и навыки детей, обучающихся ментальной арифметике по методике ISMA, соответствуют требованиям крупнейших мировых ассоциаций по ментальной арифметике. В соответствие с международными требованиями в нашей методике увеличено количество рядов, вносятся усовершенствования. Это позволяет нашим детям с блеском выступать на мировых олимпиадах.
Пробный урок по ментальной арифметике в Хабаровске 15 июня 2021 в Радужный кит
Событие добавлено в избранное
Выбрать категорию Добавить в избранноеВ развивающем центре «Радужный КИТ» пройдет пробный урок по ментальной арифметике.
Что такое ментальная арифметика? Это методика, которая недавно стала распространяться в нашей стране, но достаточно давно существует в восточных странах.
С помощью специального инструмента – счетов соробан – дети знакомятся со сложением и вычитанием, умножением и делением любых чисел: сначала на самих счетах, а потом и в уме. Даже пятилетние малыши смогут решать примеры с трехзначными числами в уме. Но очень быстрый счет – это не главная цель методики. Устный счет всегда был замечательным тренажером для мозга, который позволяет развить внимание, воображение и память, увеличить скорость обработки любой информации (не только числовой). Ментальная арифметика добавляет к этому перечню умение работать в режиме многозадачности, т.е. ребенок может считать в уме одновременно с чтением стихотворения или выполнением любых других действий.
Приглашаются дети от 5 до 16 лет на бесплатное пробное занятие. Запись обязательна.
Стоимость: бесплатно
Телефон для справок: +7-924-311-39-57.
Место проведения:ул. Краснореченская, 90 кор. 1, 2-й этаж, оф. 215
Дата
Событие
Место
Спасибо за регистрацию!
Мы отправили организатору запрос на бронирование мест на событие «Пробный урок по ментальной арифметике» 15 июня 18:00. На вашу почту и указанный в анкете телефон придет подтверждение, как только организатор одобрит заявку.
Вопросы к организатору по событию оставляйте в комментариях.

По другим вопросам пишите на почту [email protected]Спасибо за регистрацию!
Вы зарегистрированы на событие «Пробный урок по ментальной арифметике», на 15 июня 18:00
Регистрация на событие отменена
Регистрация на событие «Пробный урок по ментальной арифметике», на 15 июня 18:00 отменена.
Спасибо за регистрацию!
Мы отправили организатору запрос на бронирование мест на событие «Пробный урок по ментальной арифметике» 19 июня 15:00.
На вашу почту и указанный в анкете телефон придет подтверждение, как только организатор одобрит заявку.
Вопросы к организатору по событию оставляйте в комментариях.
По другим вопросам пишите на почту [email protected]Спасибо за регистрацию!
Вы зарегистрированы на событие «Пробный урок по ментальной арифметике», на 19 июня 15:00
Регистрация на событие отменена
Регистрация на событие «Пробный урок по ментальной арифметике», на 19 июня 15:00 отменена.
Спасибо за регистрацию!
Мы отправили организатору запрос на бронирование мест на событие «Пробный урок по ментальной арифметике» 22 июня 18:00. На вашу почту и указанный в анкете телефон придет подтверждение, как только организатор одобрит заявку.
Вопросы к организатору по событию оставляйте в комментариях.
По другим вопросам пишите на почту [email protected]Спасибо за регистрацию!
Вы зарегистрированы на событие «Пробный урок по ментальной арифметике», на 22 июня 18:00
Регистрация на событие отменена
Регистрация на событие «Пробный урок по ментальной арифметике», на 22 июня 18:00 отменена.
Спасибо за регистрацию!
Мы отправили организатору запрос на бронирование мест на событие «Пробный урок по ментальной арифметике» 29 июня 18:00. На вашу почту и указанный в анкете телефон придет подтверждение, как только организатор одобрит заявку.
Вопросы к организатору по событию оставляйте в комментариях.
По другим вопросам пишите на почту [email protected]Спасибо за регистрацию!
Вы зарегистрированы на событие «Пробный урок по ментальной арифметике», на 29 июня 18:00
Регистрация на событие отменена
Регистрация на событие «Пробный урок по ментальной арифметике», на 29 июня 18:00 отменена.
Ментальная арифметика: как и зачем решать 10 примеров в секунду
Ментальная арифметика: как и зачем решать 10 примеров в секунду
Умение быстро считать в уме развивает внимание, скорость обработки информации и даже творческое мышление. Дает ли этот навык ребёнку конкурентное преимущество в будущем? Станет ли шагом к успешной жизни или просто отнимет драгоценное время? Екатерина Цыбуля, руководитель центра «Учусь на 5», логопед, тренер по ментальной арифметике, рассказывает, в чем польза такого обучения.
Екатерина Цыбуля, руководитель центра «Учусь на 5», логопед, тренер по ментальной арифметике
Ментальная арифметика — программа развития умственных и творческих способностей, основанная на системе устного счета. Освоив ее, ребенок сможет решать арифметические задачи в уме всего за несколько секунд. Методика рекомендована для детей от 4 до 12 лет. Однако современные развивающие центры готовы обучать и более взрослых людей, как правило, с одной оговоркой — чем позднее начнешь, тем больше усилий потребуется.
Ментальная арифметика зародилась в Японии в ХVI веке. На начальных этапах обучения используются специальные счеты — абак или соробан. Счеты состоят из рамки, разделительной полосы, вертикальных спиц, верхних («небесных») и нижних («земных») косточек. Одна «небесная» косточка равна пяти «земным». Количество спиц варьируется от 13 до 31. При работе ребенок использует только большой и указательный пальцы. Все движения доводятся до автоматизма. Через некоторое время ребенок совершает вычисления на воображаемом абаке, а задачи решаются с помощью образов.
Формула интеллекта: логика плюс интуиция
Известно, что левое полушарие отвечает за логику, рациональность и анализ, а правое — за образность, целостность, интуицию, фантазию и воображение. Современная система образования уделяет больше внимания точным наукам. Время на танцы, рисование или занятие музыкой выделяется по остаточному принципу. Но даже если родителям удается найти золотую середину, возникает вопрос — как развить взаимосвязь работы обоих полушарий, чтобы максимально раскрыть потенциал ребенка?
Программа обучения метальной арифметики направлена на формирование устойчивых нейронных связей левого и правого полушарий. По мнению педагогов, именно этот факт помогает людям выбирать наиболее эффективные решения и добиваться успеха в жизни.
Плюсы и минусы ментальной математики
Самый очевидный результат обучения — способность совершать арифметические действия с шестизначными числами за несколько секунд. Но сложно представить, зачем сегодня ребенку может понадобиться этот навык. Как утверждают педагоги по ментальной математике, быстрый счет в уме — это побочный эффект, а не цель. Основная задача обучения — добиться эффекта синергии от синхронной работы обоих полушарий мозга, который превосходит эффект от работы каждого полушария по-отдельности. Тогда вместе с математическими способностями в ребенке будут развиваться:
- усидчивость
- концентрация внимания
- фотографическая память
- воображение
- творческое мышление
- скорость обработки информации
Кроме возрастных ограничений, никаких противопоказаний к занятиям нет. Однако отзывы родителей говорят о том, что не все ученики наблюдают улучшение памяти и концентрации внимания, а у некоторых детей возникают проблемы с решением элементарных задач на логику.
Здесь стоит вспомнить простую истину о том, что каждый ребенок уникален. Менар — это одна из методик развития интеллекта, которая помогает выявить и раскрыть уникальные способности ребенка. Ребенок учится быстро усваивать новую информацию, формулировать мысли и делать выводы. Тем не менее, не стоит пренебрегать традиционными играми — шахматами, головоломками, ребусами. Поэтому, наблюдайте, пробуйте, анализируйте и выбирайте то, что подходит именно вам.
Как проходит обучение
Обучение состоит из 10 уровней, каждый из которых занимает до четырех месяцев. Полный курс длится 2−3 года. Занятия идут по два академических часа один раз в неделю, кроме этого дети должны потратить 15 минут на выполнение домашних заданий. Как правило, у каждого развивающего центра есть онлайн-платформы, которые позволяют более эффективно работать самостоятельно.
Самый главный инструмент — это абак. Также в процесс обучения включают настольные, подвижные игры, просмотр мультфильмов и физминутки. На первом этапе детей учат складывать и вычитать числа на абаке. В этот период тренируется мелкая моторика, пространственное и логическое мышление. Далее переходят на ментальную карту — картину с изображением абака. И на следующем этапе дети производят арифметические действия с помощью визуализации процесса. Таким образом, уже через год ребенок может делать вычисления в уме.
Как выбрать школу ментальной арифметики?
Результат обучения будет зависеть от трех участников процесса — ребенка, учителя и родителей. Но самое главное — правильно выбрать образовательный центр, где будут преподавать менар. Вот несколько простых правил:
- Запишитесь на пробное занятие. Оцените, насколько комфортно ребенку в новых условиях. Не упустите возможность пообщаться с другими родителями.
- Познакомьтесь с педагогом. Спросите, как готовят преподавателей ментальной арифметики? Контролирует ли головной офис методику преподавания, уровень знаний педагогов, проходят ли преподаватели аттестацию на профпригодность?
- Обратите внимание на количество учеников в группе. Только в небольших группах преподаватель может уделить необходимое время каждому ученику. Поэтому в младших группах занимаются 5−7 человек, в старших — 8−10.
- Сделайте анализ рынка. Стоимость обучения в пределах одного региона не может сильно отличаться. Слишком низкая цена может быть показателем недобросовестного подхода к подготовке персонала и разработке методики. Слишком высокая цена может быть связана с издержками, дорогой арендой или рекламой.
Самое главное — чтобы ребенку нравились. Ему должно быть интересно считать, несмотря на то что считать — может быть довольно скучным занятием. Если ребенку нравится, значит, преподаватель смог заинтересовать его. Кроме этого, чтобы оценить преподавателя, обычно спрашивают: через сколько появятся первые результаты? На какие способности влияет обучение? Что делают, чтобы ускорить обучение? Хороший педагог ответит на все вопросы.
Читайте также:
Ну и почерк! Почему детям всё-таки важно учиться красиво писать?
11 полезных советов для родителей от педагога по английскому языку
Зачем детям учить математику?
Фото: GRSI, Ann in the uk, NadyaEugene/Shutterstock.com
Уроки ментальной арифметики для детей: бесплатные видео для домашнего обучения
Уроки ментальной арифметики для детей: бесплатные видео для домашнего обучения
Ментальная арифметика – популярная методика гармоничного и равного развития обоих полушарий мозга. Методика одинаково подходит для детей и взрослых и заключается в обучении быстрому устному счету с применением специального инструмента, который называют абакусом или соробаном.
Научить детей ментальной арифметике в домашних условиях помогут видео уроки на сайте ВСЕ КУРСЫ ОНЛАЙН.
Строение и функции абакуса (соробана)
Абакус – древние китайские счеты. Состоит из рамки, перекладины, спиц и косточек. Перекладина делит косточки горизонтально на 2 части. Нижние получили название «земных» (смотрят всегда вниз), верхние – «небесных» (смотрят вверх). Косточки играют роль единиц, десятков и сотен. Сначала ученики осваивают простые арифметические действия (сложение и вычитание), затем сложные (умножение и деление). Следующий этап – счет без использования инструмента, в уме. Ученик двигает пальцами, представляя абакус, и решает примеры с многозначными числами. Инструмент можно запросто сделать самостоятельно, переконструировав обычные советские счеты.
Основные принципы
- Считать правильно двумя руками, используя указательные и большие пальцы.
- Поднимают кости всегда большим пальцем, опускают и двигают «небесные» косточки указательным.
- Абакус нужно придерживать левой рукой.
- В правой руке всегда находится ручка для заметок и записей, обхваченная мизинцем, безымянным и средним пальцами.
- Сброс косточек в исходное положение делают, обхватив перекладину двумя рабочими пальцами и двигаясь справа налево.
Набор чисел
Крайний правый столбец предназначен для набора единиц, второй для десятков, третий для сотен, следующие для тысяч и так далее. Исходное положение означает ноль. Поднятые нижние бусины – единицы от 1 до 4, десятки от 10 до 40 и аналогичные сотни, тысячи в зависимости от столбца. Верхние опущенные бусины обозначают числа, кратные пяти: 5, 50, 500, 5000 и т.д. по мере удаления столбцов. Цифра 7 – это 5+2. Значит нужно опустить небесную косточку и поднять две земных. Все остальные числа набирают по аналогичному принципу. Для тренировки хорошо использовать онлайн-тренажеры в Google или установить специальное приложение.
Правила
Правила имеют условные названия, которые образно иллюстрируют действия. Выполняются всегда в строгой последовательности.
- «Просто» — поднятие нужного количества земных косточек, опускание небесной или то и другое одновременно.
- «Брат» — когда первый пункт не работает и сумма выдает 5.
- «Друг» — два числа, дающие 10.
- «Друг + Брат» — совмещает два предыдущих правила, выполняется двумя руками.
Сложение (простое и с переходом на 10)
Самое простое действие, с которого начинают обучение. Начинать первое знакомство можно в детском саду, начальной школе. Сначала следует научиться считать до 10. Затем решать примеры до 3. Следующий этап — сложение всех чисел без перехода на десятки. В качестве закрепляющих заданий эффективно использовать карточки с изображениями разных комбинаций на счетах. Например, найти правильный ответ на заданный пример. При сложении за пределами десятка суммы необходимо разложить на простые составляющие. Состав десяти может иметь несколько комбинаций (1+9, 2+8, 3+7, 4+6, 5+5).
Вычитание
Разницу считают подобно сумме, по правилам «просто», «брат», «друг», «друг+брат». Существует масса онлайн тренажеров и конструкторов заданий для закрепления арифметических навыков. Современные ученики обожают работать на компьютере, поэтому заставлять тренироваться даже не придется. Будущие математики сами с удовольствием будут выполнять нужные упражнения.
Умножение
Умножение (многократное сложение) можно выполнять несколькими различными методами. Самый простой и безошибочный был предложен Японским Комитетом по абакусу. Принцип напоминает умножение в столбик на бумаге, так же последовательно. Чтобы работать с двузначными числами (45*56), нужно учесть: ответ получится четырехзначным, и нужно будет уметь его прочитать.
Деление
Деление производят по принципу многократного вычитания. Конечно, без выученной «на зубок» таблицы умножения приступать к действию не имеет смысла. Самый удобный метод разработан Такаши Койима в книге об использовании и теории японского абакуса. Главный плюс — использование привычной школьной терминологии: делимое, делитель, частное. Делимое находится правее центра, делитель левее, разделенные тремя-четырьмя свободными линейками.
Положительное влияние счета на абакусе
В Азии предмет входит в обязательную программу почти во всех учебных заведениях. С помощью простого девайса дети учатся умножать и делить многозначные числа без калькулятора. Существуют и другие сопутствующие бонусы.
- Развивается зрительная и слуховая память, повышается внимание и сосредоточенность.
- Активируется интуиция, сообразительность, смекалка.
- Возникает нестандартное мышление, самостоятельность, уверенность в принятии решений.
- Усиливаются творческие способности и предрасположенность к изучению иностранных языков.
Тренировочные упражнения
Благодаря японской методике родители имеют прекрасную возможность одновременно учить детишек счету и прокачивать ум и интеллект в целом. Европейцы подхватили идею и дополнили интерактивными технологиями: компьютерным тренажером (анзаном), флеш-картами и другими программами. Важно заниматься каждый день в течение двух-трех лет , начиная с четырех-шестилетнего возраста.
В результате регулярных занятий повышается успеваемость в школе за счет улучшения памяти и повышения концентрации внимания. Ребенок легче запоминает новые слова, исторические даты и факты, теоремы и формулы. Одновременно развивается воображение и творческое мышление, способность нестандартно подходить к решению задач.
Видео-уроки | SmartyKids
Детское развитие и дополнительное образование – одно из прибыльных направлений бизнеса. Но построить онлайн-школу или офлайн-центр с нуля – очень сложная задача для человека без опыта. Мы предлагаем франшизу SmartyKids. За пять лет успешной работы мы открыли свыше 300 центров в шести странах.
Для кого франшиза SmartyKids.
SmartyKids – это франшиза с минимальными вложениями и быстрой окупаемостью. Нашими партнерами могут стать родители, педагоги, предприниматели, собирающиеся открыть свой учебный центр для детей.
В рамках франшизы компания предлагает обширный пакет сопровождения:
· Доступ к авторским методикам для офлайн и онлайн обучения. Они включают программы по ментальной арифметике, программированию, финансовой грамотности, скорочтению, каллиграфии.
· Профессиональные учебные материалы высокого качества.
· Доступ к обучающей онлайн платформе с личными кабинетами педагога и ученика.
· Макеты для рекламных кампаний и оформления центра.
· Резюме педагогов, обучение педагогов фирменным методикам.
· Собственный сайт, crm-систему, еженедельные конференции, чаты поддержки и многое другое.
Преимущества сотрудничества с компанией SmartyKids
Главное достоинство нашего предложения – франшиза с минимальными вложениями и быстрой окупаемостью. Работа под нашим брендом позволяет открыть успешный детский центр в любом городе или районе страны. Среди прочих наших преимуществ:
· Универсальность. Занятия можно проводить как удаленно, так и в классах. Из-за периода пандемии мы существенно снизили требования к площади центров. На сегодняшний день достаточно совсем небольшого помещения, чтобы начать работать офлайн.
· Полная поддержка по всем вопросам ведения бизнеса. Делимся опытом, накопленным нашей сетью за 5 лет успешной работы. Это помогает избежать большинства распространенных ошибок и за более короткий срок выйти на полную окупаемость вложений в открытие. Как правило, этот срок составляет от 3 месяцев.
· Сильный бренд и хорошая репутация. Наш бренд знают и любят по всей стране. Через сеть центров прошло уже более 20 тысяч детей в 220 городах. В рамках сети было проведено более 20 олимпиад, мы подготовили свыше 2 тысяч педагогов. Мы постоянно работаем над повышением уровня знания бренда SmartyKids увеличением лояльности потребителей.
Если вы давно хотели открыть собственное дело, но не решались начать – мы окажем комплексную поддержку. Это собственный бизнес с небольшими стартовыми затратами и обширными перспективами в будущем.
Оставьте заявку или звоните нам. Мы расскажем про все условия и возможности подробнее, и поможем вам выбрать оптимальный формат сотрудничества.
Лучшие онлайн-курсы и бесплатные тренажеры по ментальной арифметике для детей
Ментальная арифметика сегодня на пике популярности. В каждом городе появляются новые развивающие центры, в уже существующих создаются специальные курсы. Однако, развивать умственные способности можно и в привычной домашней обстановке — есть большой выбор онлайн-курсов и тренажеров по ментальной арифметики.
Начать обучаться можно в любом возрасте. Занятия на курсах состоят из нейродинамической гимнастики, активного счета и комплексных упражнений. В результате систематических занятий дети значительно улучшают показатели по всем дисциплинам, также у них улучшаются зрительная, слуховая, визуальная память, повышается концентрация внимания.
Онлайн-школы
Hedu
Онлайн-курс по ментальной арифметике «Просто». Уровень: Начинающий
Ребенок научиться считать в уме и на абакусе, сформирует новые нейронные связи и разовьет оба полушария мозга.
После окончания курса ребенок сможет:
- Считать на абакусе от 1 до 999
- Улучшить память
- Улучшить концентрацию внимания
- Развить аналитические способности
- Быстро считать в уме
- Нестандартно мыслить
Программа
- Урок № 1 — Что такое ментальная арифметика
- Урок № 2 — Складываем единицы «Просто»
- Урок № 3 — Десятки 10 – 50
- Урок № 4 — Двузначные числа 10 – 55
- Урок № 5 — Однозначные 6 – 9. Десятки 60 — 90
- Урок № 6 — Двузначные 55 – 99
- Урок № 7 — Двузначные 10 – 99
- Урок № 8 — Трехзначные «100-500»
- Урок № 9 — Трехзначные числа на абакусе
- Урок № 10 — Считаем трехзначные в уме
- Урок № 11 — Отработка счета сотен
- Урок № 12 — Сотни 600 – 900
- Урок № 13 — Отработка счета трехзначных чисел. Ментальный счет от 600 до 999
- Урок № 14 — Счет в уме и на абакусе чисел от 1 до 999
- Урок № 15 — Подготовка к тестовой работе. Тест по теме «Просто»
Международная сеть школ Абакус-центр
Программа обучения «Абакус»
Стандартная программа 2-2,5 года обучения
- Знакомство с абакусом
- Знакомство с цифрами 1- 9, а так же двузначными числами.
- Постановка руки (прописи), развитие мелкой моторики и межполушарного взаимодействия, развитие речи
- Развитие концентрации внимания, образного мышления, фотографической и слуховой памяти через применение образов (флешкарт) и ментального счета
- Развить математических способностей благодаря заданиям на логику и пространственное мышление
- С помощь развивающих игр тренируем смекалку, внимание и наблюдательность.
- Раскрепощенность через групповые игры и упражнения Брейн Фитнес
- Работа в группе помогает детям улучшить навыки коммуникации и взаимодействия.
- Сложение и вычитание двузначных чисел простым методом
- Любовь к цифрам и в целом к обучению
- Занятия способствуют развитию внутренней мотивации обучения.
Первая Детская Онлайн Школа
Сайт: https://detkishkola.ru
Телефон: +7 (952) 193-92-05
Стоимость: от 4000р. в месяц
Школ ментальной арифметики много, однако заниматься счетом в уме в любое удобное время и из любой точки мира русскоязычным деткам предлагают немногие.
Домашний онлайн-курс ментальной арифметики: как преподаватели это делают?
- Понятно, доступно и нескучно:) Онлайн-курс обучения в школе длится 3 месяца.
- Обучение проходит онлайн в формате видео-урок и длится до 30 минут, 2 раза в неделю по вторникам и четвергам в 9 часов утра по Москве. Все занятия доступны в любое удобное время для просмотра.
- Раз в неделю приглашаются родители учеников на онлайн-вебинар с преподавателем, где вы сможете получить ответы на свои вопросы.
- Каждый урок можно в любое время просмотреть в записи в течение месяца.
- Домашние задания в соответствии с уровнем и возрастом дети выполняют на онлайн тренажере в личном кабинете, а учитель их проверяет и дает допуск к следующему занятию.
Mental Shool
Ребёнок занимается в комфортных для него условиях,
в удобное для него и для Вас время. Вы не пропускаете занятия, даже если отправитесь в отпуск или к бабушке на каникулы. Вы можете заниматься вместе с ребёнком,
совместное обучение сблизит Вас еще больше.
Освоить всю методику можно и НУЖНО всего за 12 месяцев! Цена за полное освоение Ментальной Арифметики + методика Нейрогимнастики для усиления, выходит в 4 РАЗА ДЕШЕВЛЕ и быстрее! Занимаясь короткими 30-ти минутными уроками,
два раза в неделю.
Усовершенная Ментальная Арифметика
Очень проста и понятна в усвоении. Даже для детей 4х лет. Идентична и гармонична со школьной программой, обычный состав числа 5 и 10.
Академия ментальной арифметики
Кому будет полезен этот курс?
- Педагогам детских развивающих центров и клубов
Сразу после обучения сможете запустить новое прибыльное направление в вашем клубе - Желающим стать преподавателями
Пройдя обучение у нас, Вы сможете стать педагогом в частных и государственных детских организациях или вести индивидуальные занятия - Тем, кто хочет заниматься самостоятельно
Ментальная арифметика полезна в любом возрасте, всемирно признана как профилактика от болезней головного мозга, в том числе болезни Альцгеймера.
После прохождения курса и сдачи экзамена Вы получите сертификаты: международный сертификат GyMind на английском и русском языках как специалист по ментальной арифметике с правом преподавания + сертификат установленного образца о повышении квалификации.
Они подтверждают вашу квалификацию с указанием пройденных дисциплин и количеством часов обучения.
Образовательный центр Sirius Future
Сайт: https://siriusfuture.ru
Телефон: +7 499 283-63-78
Стоимость: от 3960р. за 4 занятия
Методика быстрого счета в уме, благодаря которой, ребенок учится выполнять арифметические действия ментально: 567+1378 — 986 = ?
Кроме этого уроки направлены на развитие когнитивных способностей (память, мышление, логика, внимание) и всестороннее развитие ребенка.
Как устроен процесс обучения?
Занятия с преподавателем по видеосвязи
Все занятия по ментальной арифметике проходят на интерактивной онлайн платформе.
Необходимые задания и упражнения внедрены в платформу.
К каждому ребенку индивидуальный подход.
Домашняя работа
После каждого занятия для закрепления полученных знаний, ребенок получает домашнюю работу.
Успеваемость ребенка
Родители получают подробный отчет после каждого занятия, а именно, что ребенок изучал на уроке и на каком уровне находится.
Онлайн-школа «Супер-мама»
Что дает ментальная арифметика?
- Быстрый устный счет
- Умение концентрировать внимание надолго
- Усидчивость
- Развитие памяти, воображения
- Уверенность в себе
- Уверенность в возможности достижения любых поставленных целей
- Повышение успеваемости по всем предметам
Что предлагает онлайн-школа:
Протестированная система преподавания
Учебные материалы для 3-х возрастных категорий
Система дополнительных заданий, направленных на развитие памяти, логики, внимания
Комплекс упражнений зрительной и дыхательной гимнастики
Онлайн-школа «Быстрее всех»
Творческий подход — Ребенок учится мыслить нестандартно и вырабатывать индивидуальный подход к каждой задаче
Аналитическое мышление — Мысли и действия ребенка направлены на установление причинно-следственной связи и действие согласно анализу. Осмысленное запоминание — Ребенок запоминает информацию, понимания логику связеобразующих частей и самого материала.
В ЧЕМ ПРЕИМУЩЕСТВА МЕНТАЛЬНОЙ АРИФМЕТИКИ НАД ШКОЛЬНОЙ ПРОГРАММОЙ?
Все просто: в то время как школьная программа направлена исключительно на развитие левого полушария мозга, ментальная арифметика стимулирует оба полушария одновременно, развивая как логику, так и творчество. Два в одном!
Польза для вашего ребенка:
- Развитие интеллекта
- Повышение концентрации
- Совершенствование памяти
- Улучшение успеваемости
- Подъем самооценки
- Рост популярности
Академия развития интеллекта «Амакидс»
Сайт: https://amakids.ru
Телефон: 8 (800) 500-39-79
Стоимость: не указана
Курсы ментальной арифметики в «Академии развития интеллекта AMAKids» – это:
- Высококвалифицированные тренеры, которые прошли строгий конкурсный отбор и досконально знают все нюансы методики.
- Интересные и увлекательные занятия, которые проходят в игровой форме.
- Небольшие группы до 10 человек, что обеспечивает индивидуальный подход к каждому ребёнку.
- Красочные учебники.
- А также уникальная платформа, с помощью которой результат достигается в 2-3 раза быстрее.
Если вашему ребёнку исполнилось 5 лет, он умеет считать от 0 до 10 в прямом и обратном порядке, а также умеет соотносить цифру с количеством, то его уже можно записать на пробное занятие по ментальной арифметике в «Академии развития интеллекта AMAKids»! Первое же упражнение будет для вашего ребёнка шагом в мир удивительных возможностей.
Дистанционная школа «School Inter»
Ментальная арифметика преподается детям от 6 до 12 лет. Это возраст интенсивного развития мозга.
Ведет занятия сертифицированный специалист — Светлана Чернова, педагог по образованию много лет обучающая детей английскому языку. «Меня впечатляют современные дети и возможности, которые перед ними открываются, благодаря уникальным методикам, можно вырастить настоящих гениев, я уверена, что детей ждет очень интересное и счастливое будущее!»
Для занятий понадобятся счеты Абакус.
Этот курс разработан специально для регулярных занятий родителей вместе со своими детьми, так как понадобится отрабатывать новые навыки каждый день без перерывов на праздники и выходные дни. Помимо умения считать вы будете учиться развивать с детьми правое и левое полушарие головного мозга, играть в игры на развитие внимания и памяти, получим много интересных и полезных навыков для интеллектуального и умственного развития личности.
Высшая Школа Гениев
Сайт: https://genius.bz
Телефон: 8 800 333 49 21
Стоимость: не указана
Учебный центр «Высшая Школа Гениев» был основан с целью позволить каждому ребенку и взрослому в России стать гением.
Цикл занятий по курсу «Маленький Гений» и «Ментальная арифметика для педагогов» подготовлен сертифицированными преподавателями международного уровня учебного центра «Высшая Школа Гениев», лидера России на рынке обучения ментальной арифметике онлайн.
Обучение, курсы, семинары, дистанционные занятия, уроки, онлайн по ментальной арифметике для взрослых, педагогов, учителей, преподавателей, родителей и учебных центров
можно пройти у нас в живую и дистанционно в «Высшая Школа Гениев». Также для удобства предоставляются учебники по ментальной арифметики, пособия, учебные материалы, абакусы, соробан и другие материалы необходимые для обучения.
Тренажеры:
Друг Доктор
Ментальная арифметика (быстрый счёт) онлайн — тренажёр и теория.
Настоящий курс ментальной арифметики (быстрого счёта) основан на наиболее эффективных приёмах быстрого счета, разработанных профессиональными математиками.
Если вы хотите научиться выполнять арифметические операции исключительно в уме с поразительной скоростью, а также овладеть математическими трюками, которые дадут вам преимущества в повседневной жизни и удивят ваших друзей, то этот курс для вас.
В отличие от активно рекламируемых платных курсов ментальной арифметики с использованием абакуса, предлагаемая методика подразумевает творческий подход к изучению приёмов быстрого счёта, что ведёт к развитию мышления и памяти.
Каждый из уроков курса состоит из теоретической части и практических занятий на онлайн-тренажёре.
Данный курс ментальной арифметики подходит как для взрослых, так и для детей.
Клуб Ментальной арифметики
Основные возможности тренажера
- Автоматическая генерация примеров на основе заданных параметров
- Сложение, вычитание, умножение, деление
- Любое сочетание законов на 5 или 10
- Произвольное количество разрядов для чисел
- Десятичные дроби для умножения и деления
- Показ числе на счетах для начинающих
- Возможность настройки временных интервалов
- Индивидуальный и групповой режим
- Показ примеров на случайном месте экрана, изменение шрифта и цвета
- Расчет времени окончания всего теста
- Озвучивание цифр и подсказок
- Распознавание ответов с помощью микрофона. Возможность управлять процессом исключительно голосом
- Работа на мобильных устройствах
- Сохранение настроек в браузере
Легкие числа
Бесплатный месяц обучения ментальной арифметике
- доступ к обучению на срок 1 месяц
- пошаговые задания на каждый день
- текстовые и видео уроки
- полный доступ к тренажеру для обучения ментальной арифметике с помощью счет абакус/соробан
- консультации по e-mail
Полный доступ к игре на 1 месяц (3 USD)
- доступ к обучению на срок 1 месяц
- полный доступ к тренажеру для обучения ментальной арифметике с помощью счет абакус/соробан
Обучение ментальной арифметике 1 месяц (5 USD)
- доступ к обучению на срок 1 месяц
- пошаговые задания на каждый день
- текстовые и видео уроки
- полный доступ к тренажеру для обучения ментальной арифметике с помощью счет абакус/соробан
- консультации по e-mail
Соробан77.ру
«Тренировочный режим» онлайн-тренажера предназначен для практического закрепления знаний по полному курсу теории «Соробан», т.е. рассчитан на пользователя, успешно освоившего все восемь уровней. Порядок пользования онлайн-тренажером приведен ниже:
- В окне онлайн-тренажера необходимо ввести исходные данные для работы
- В поле ввода «КОЛИЧЕСТВО ЧИСЕЛ» вводится любое целое число от «3» до «99», которое определяет желаемое количество последовательно выводимых на экран чисел.
- В поле ввода «ЗАДЕРЖКА» вводится любое целое число от «1» до «30 000», которое определяет интервал времени между выводом на экран предыдущего и последующего значений, выраженный в миллисекундах.
- В поле ввода «ОТ» вводится значение минимального разряда выводимых чисел (от «1-значные» до «5-значные») путем выбора одного из значений в выпадающей вкладке.
- В поле ввода «ДО» вводится значение максимального разряда выводимых чисел (от «1-значные» до «5-значные») путем выбора одного из значений в выпадающей вкладке.
Угадайка
Представляем вам интерактивный обучающий сайт, с элементами которого можно взаимодействовать, для изучения арифметики с помощью абакуса (соробана). Абакус — это отличный инструмент, чтобы научиться быстрому счету и особенно может быть полезен для школьников младших классов. Идея заключается в том, чтобы отойти от «скучных» и «сухих» цифр и перейти к «образному счету». С помощью бусинок абакуса у человека возникают образы для каждого математического действия.
Образы намного лучше запоминаются, чем просто цифры и математические знаки.
Человеческий мозг работает с образами в разы быстрее чем с простым счетом «на пальцах».
Последовательно выполняя одно задание за другим, вы сможете освоить принцип счета на абакус и помочь вашему ребенку сориентироваться, как считать на абакусе (соробане).
Первопроходцы в математике
Принадлежности для студентов
20 соединительных кубиков
телефонная линия (0–40)
Материалы для учителя
Отображение меню стратегий вычитания (Учебное пособие) Страница 419
Подготовленный набор карточек вычитания из маленьких чисел 1–6 Мастера (руководство для учителя) дополнительно
2–5 подготовленных наборов и демонстрационный набор из маленьких десяти рамочных карточек 0–10 Masters (Руководство для учителя).См. Подготовка материалов.
2–5 подготовленных наборов и демонстрационный набор из десятикадровых флеш-карт 11–20 Masters (Руководство для учителя). См. Подготовка материалов.
Блок 12 Протокол оценки
Блок 12 Индивидуальный отчет оценки
строка номера класса (0–130)
лента
диаграмма
Подготовка материалов
Подготовьте три диаграммы. Покажите и напишите на каждом листе диаграммы один из следующих заголовков: «Подсчет», «Обратный отсчет» и «Рассуждение».
Приготовьтесь показать свои стратегические карты. Сделайте 15 копий карты Show Your Strategy Cards Master и разрежьте их отдельно, так что у вас есть 60 карт. Запишите отдельный факт вычитания на каждую карту из карт вычитания для Маленькие числа 1–6 Мастера. Держите карточки отсортированными по группам (например,g., Группа 1 соответствует вычитанию Карты для маленьких чисел 1 Мастер). См. Рисунок 1.
Рисунок 1: Подготовлено Покажите свою стратегическую карту
Наконечник TIMS
Если у вас небольшой класс, запишите только некоторые задачи на вычитание. Выбирайте факты, которые поддаются разному подсчету и стратегии рассуждений.
Подготовка материалов для учебных центров. Студенты будут иметь доступ к нескольким различным мероприятиям учебного центра в этом уроке. Сделайте знак, обозначающий деятельность каждого центра. Решите, сколько студентов посетят центр в один раз, подготовьте для каждого занятия следующие материалы и поместите их в учебный центр.
Первый класс Урок 10 Больше и 10 Меньше
У меня ученики используют базовые десять блоков для моделирования 35 и 36.Помогите ученикам подумать о своих числах:
- Какое число меньше: 35 или 36? ( 36 )
- Как ваша модель показывает, что 35 меньше 36? ( 35 имеет меньше единиц, чем 36 )
- Какое число на единицу больше 36? Откуда вы знаете? ( 37 — это еще один, он идет сразу после 36, когда я считаю. )
Прочтите классу следующую задачу: У Тони 22 маркера. У Пэта на 10 маркеров меньше, чем у Тони. У Яна на 10 маркеров больше, чем у Тони.Сколько маркеров у каждого ребенка?
- Как вы можете использовать модель, чтобы найти количество маркеров, которые есть у Пэта? (У Пэта на 10 меньше, чем у Тони, поэтому я начинаю с показа маркеров Тони. У него 22, 2 десятки и 2 единицы. Если я уберу 1 десятку, останется 1 десятка и 2 единицы, или 12. )
- Как мы можем использовать модель, чтобы определить, сколько маркеров у Яна? (У Яна на 10 больше, чем у Тони. У Тони 2 десятки и 2 единицы. Если я добавлю 1 десятку, то у Яна будет 3 десятки и 2 единицы, или 32 маркера)
Я предлагаю ученикам нарисовать картинку, чтобы показать, сколько маркеров есть у каждого ребенка.Укажите, что есть более быстрый способ решить нашу проблему, чем писать или рисовать.
- Когда мы находим на 10 больше или на 10 меньше, что происходит с количеством единиц? ( Они остались прежними. )
Объясните: поскольку цифра десятков изменяется только на 1, мы можем найти на 10 больше или 10 меньше, мысленно прибавляя или вычитая 1 к числу десятков.
Я моделирую это, выбирая число и прося студентов определить, какое число на 10 больше, а какое на 10 меньше.Например — я пишу на доске цифру 33, и рисую десятки и единицы. Нарисуйте число, которое на 10 больше и на 10 меньше.
- Что показывают цифры слева? ( 2 десятка 3 единицы, 23 )
- Как в сравнении с моделью на 33? ( В нем на единицу меньше десяти .)
- Как числа показывают, что 43 на 10 больше, чем 33? ( Разряд десятков меняется с 3 на 4. Это означает, что на 1 больше, чем в 43, чем в 33. )
- Какое число на 10 больше 43? ( 53, разряд десятков меняется с 4 на 5.)
Сложить мысленно целые числа — Полный курс арифметики
435 + 461 = 896
Сначала сложите сотни, затем десятки, затем единицы.
Теперь мы видим фундаментальный принцип всех мысленных вычислений:
Считайте слева направо, как вы читаете.
Последнее число, которое вы скажете, — это ответ
Пример 5. Счет по десяткам. 30 + 24 = 54.
Вот другие примеры:
20 + 16 = 36
40 + 38 = 78
40 + 62 = 102
40 + 82 = 122
90 + 73 = 163
Пример 6. 43 + 25
Сначала добавьте десятки, затем единицы. Скажите
«Шестьдесят —
43 + 25
— восемь.«
Или, можно сказать,
«43 плюс 20 равно 63, плюс 5 равно 68».
Скажем: «150 плюс 7 равно 157.»
Скажите только: «50 плюс 14 — 64».
Искусство мысленного расчета — говорить как можно меньше. Последнее число, которое вы скажете, и есть ответ.
«170 плюс 11 равно 181.»
Пример 10.23 + 32 + 25 + 12
Сначала сложите все десятки, затем добавьте единицы. Добавляя каждое место, называйте частичную сумму. Скажите
Последнее число, которое вы скажете, — это вся сумма.
| Пример 11. | 34 + 25 + 32 |
| «50, 80, 89, 91 .« | |
Пример 12. 653 + 224
Сначала сложите сотни, затем десятки, затем единицы. Снова произнесите каждую частичную сумму:
653 + 224
Скажем,
«800, 870, 877 .»
Пример 13. Три трека на компакт-диске имеют следующие времена:
10:34
6:25
8:07
Сколько всего времени?
10:34 означает 10 минут 34 секунды.60 секунд = 1 минута.
(Следовательно, 72 секунды = 1 минута 12 секунд. 1:12.)
Техника. Начните с минут и сосчитайте:
«16 плюс 8 — это 24 минуты».
Теперь прибавьте секунды.
«24:59 плюс 7 равно 24: 66. «
Общее время 25 минут 6 секунд.
На этом этапе, пожалуйста, «переверните» страницу и выполните несколько задач .
или
Перейти к разделу 2:
Сложите мысленно, округлив
Введение | Главная | Содержание
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Мэрилин Бернс: ментальная математика | Scholastic
Каждый день в мире взрослых мы сталкиваемся с ситуациями, требующими сложения, вычитания, умножения или деления.Мы придумываем подсказки в ресторанах, решаем, когда уйти из дома, чтобы успеть в кино, оцениваем цену товара на распродаже, отслеживаем, что мы тратим, делая покупки в супермаркете, удваиваем и делим вдвое рецепты и т. Д. . По крайней мере половину времени мы делаем эти расчеты, когда мы на улице, без ручки и бумаги под рукой, а это значит, что мы должны думать мысленно. Поскольку мыслить в уме — это такой важный жизненный навык, он должен играть регулярную роль в вашем обучении математике в классе.
Математика без карандашейКогда я хочу поработать со студентами над умственными математическими навыками, мы делаем то, что я называю «математикой за столом». Идея простая. Попросите студентов убрать все и положить руки на стол. Ни бумаги, ни карандаша, ни манипуляторов, ни книг. Затем представьте им проблему, которую нужно решить в их голове. Вот как:
Чтобы поддержать детей и убедиться, что это возможность для обучения, а не тестовая ситуация, сделайте решение проблемы усилием класса.Предложите учащимся поделиться своими идеями и услышать мнение своих одноклассников. Тем временем следуйте инструкциям и записывайте идеи студентов на доске. Запись дает вам возможность продемонстрировать учащимся, как математически представить их мышление. Когда вы это сделаете, вы обнаружите, что учащиеся быстро привыкнут к рутинной математике за столом. Затем вы можете использовать его для всего урока математики или его части, чтобы решать различные задачи по математике.
Ментальная математика в действииДля практической математики подходят всевозможные задачи, если их можно решить мысленно.Даже задачи, которые не сразу кажутся подходящими для ментальной математики, можно превратить в практические задачи. Например, задача умножения 148 x 21 не подходит, если цель — найти точный ответ. Но представить это как задачу оценивания — хороший вызов для четвероклассников. Попробуйте написать на плате такую задачу:
Какой ответ ближе всего к продукту?
148 x 21 = 1000
2 000
3 000
4 000
5 000
Дайте учащимся несколько минут, чтобы они могли спокойно подумать.Затем попросите их повернуться и поговорить с партнером или небольшой группой. Проведите обсуждение в классе, призывая учащихся делиться идеями. Поощряйте их объяснять свое мышление. Математически изобразите идеи на доске. Например, если ученик предлагает, что 1000 не может быть ближайшим, потому что 148 умножить на 10 равно 1480, напишите на доске «148 x 10 = 1480». Продолжайте обсуждение, пока все ученики не поделятся идеями и не поймут, почему 3000 — лучшая оценка. Даже если учащиеся разделяют одну и ту же идею, им полезно объяснить ее своими словами.
В качестве дополнительного задания попросите студентов объяснить на бумаге решение проблемы. Студенты могут выбрать умножение, чтобы найти точный ответ. Они также могут относиться к тому, что вы записали на доске.
Как правильно ответитьДля некоторых задач точный ответ — это цель. Спросите у первоклассников, как они вычислили бы сумму двух однозначных чисел, например, 6 + 7, — это хороший способ сосредоточить внимание учащихся на различных стратегиях сложения.Или дайте задание на сложение с двумя двузначными числами, например, 26 + 57, и попросите учащихся объяснить, как они находят сумму.
Чтобы разнообразить практику сложения, дайте ученикам двузначное число и попросите их вычислить, сколько еще нужно, чтобы получить 100. Или дайте им большее число, 578 или 1375, и спросите их, как они могли бы переименовать его в сумма двух меньших чисел или, при необходимости, сумма трех меньших чисел. Несмотря на то, что все эти проблемы требуют точных ответов, учащиеся могут найти решения разными способами.Услышав идеи других, студенты расширяют свой собственный репертуар для вычислений, что помогает поддерживать их чувство числа и повышает гибкость.
Некоторые задачи не требуют от учащихся выполнения одного конкретного вычисления, а требуют от них выполнения нескольких вычислений для проверки различных возможностей. Например, перечислите семь различных величин и попросите студентов придумать числовое предложение, в котором используются три из них. Вот пример, в котором деньги используются в качестве контекста:
В числовом предложении используются три следующих значения: $ 1.50, 2, 3,75 доллара, 50 центов, 6, 3 доллара, 75 центов. Что может быть числовым предложением? Одно из возможных решений: 3,00 доллара США ÷ 2 = 1,50 доллара США.
Деньги предоставляют полезный контекст для решения многих проблем. Вот некоторые проблемы, для которых есть несколько правильных решений.
• Как вы могли потратить ровно 100 долларов, купив две вещи по разной цене?
• Как вы могли потратить ровно 100 долларов, купив три вещи по разным ценам?
• Как вы могли потратить ровно 100 долларов, купив три вещи по разной цене, если одна из них стоит 39 долларов?
Некоторые задачи не требуют вычислений, но все же способствуют интересным обсуждениям, которые помогают учащимся лучше понять числа.
Число округлено до 1 200. Какой может быть номер?
или:
Я записал число с одним нулем, но не могу вспомнить, что это было. Я знаю, что это было от 500 до 800. Какое могло быть число?
Для всех задач поощряйте студентов объяснять свои рассуждения, даже если они дают правильные ответы. Слишком часто ученики узнают, что учителя просят их только объяснить, когда они ошибаются. В практической математике объяснения всегда важны для всех учащихся.
Отслеживание математического мышленияСлишком часто учащиеся рассматривают работу с бумагой и карандашом просто как время для отработки навыков. Конечно, есть время для практики вычислений с использованием бумаги и карандаша, но также полезно подумать о работе с бумагой и карандашом более широко. Письмо учащихся также должно быть средством, позволяющим им отслеживать свое мышление. Студенты, занимающиеся записью в результате практической математики, подтверждают это.
Mental Math is Test PrepЧтобы подготовить студентов к стандартным тестам, большинство учителей распространяют буклеты с практикой.В следующий раз вместо этого попробуйте математику за столом. Напишите проблему на доске, но не записывайте варианты ответов. Вместо этого проведите обсуждение за столом, пока класс не придет к согласию с решением. Затем отправьте ответы. Затем обсудите другие варианты, которые были неправильными, и поговорите — опять же, положив руки на стол — о том, какие ошибки могут привести к выбору неправильного ответа. Ваши ученики будут поражены их умственной силой!
7 практических советов по ментальной математике (которые может использовать ЛЮБОЙ!)
Скорее всего, вы слышали о ментальной математике — способности производить вычисления в уме — и о том, как важно для детей ее выучить.Но почему это важно? Потому что ментальная математика связана с ЧУМСТВОМ ЧИСЛА: способность манипулировать числами в голове различными способами для выполнения вычислений. В свою очередь было доказано, что чувство числа предсказывает успехи студента в алгебре. По сути, то, что мы делаем с переменными в алгебре, аналогично тому, что учащиеся могут научиться делать с числами в младших классах.
Люди с пониманием чисел гибко используют числа . Они могут разбирать их и складывать различными способами для проведения расчетов.Это очень похоже на умение «ИГРАТЬ» словами, чтобы составлять интересные предложения, или умение играть с аккордами и мелодиями, чтобы сочинять песни.
Но ментальная математика / числовое чутье не только для «математических гениев» — как раз наоборот! Выучить основы может КАЖДЫЙ, и это значительно упростит изучение математики и алгебры! Мы ожидаем, что наши дети выучат много английских слов и смогут складывать эти слова разными способами в предложения, так почему бы не ожидать, что они сделают то же самое с числами? И они могут, если им показывают основы и показывают примеры того, как это происходит.Итак, давайте перейдем к практической части этого письма: математические стратегии для ВСЕХ.
- «Девятка».
Чтобы прибавить 9 к любому числу, сначала прибавьте 10, а затем вычтите 1. В моих книгах по Math Mammoth я рассказываю детям эту сюжетную линию, где девять очень сильно хотят быть 10… поэтому он просит это другое число вместо «единицы». Другое число становится на единицу меньше. Например, мы меняем сложение 9 + 7 на 10 + 6, что намного проще решить.
Но этот «трюк» расширяется.Вы можете придумать простой способ сложить 76 + 99? Измените его на 75 + 100. Как насчет 385 + 999?
Как бы вы сложили в голове 39 + 28? Пусть 39 станет 40… что уменьшает 28 до 27. Теперь сложение 40 + 27. Еще один способ — подумать о компенсации: 39 — это на единицу меньше 40, а 28 — на два меньше, чем 30. Итак, их сумма на три меньше чем 70.
- Двухместные + 1.
Поощряйте детей запоминать двойные числа от 1 + 1 до 9 + 9. После этого у них под рукой появляется множество других фактов сложения: те, которые мы можем назвать «двойные плюс еще один».Например, 5 + 6 на единицу больше, чем 5 + 5, или 9 + 8 просто на единицу больше, чем 8 + 8.
- Используйте факты сложения при сложении больших чисел.
Как только вы узнаете, что 7 + 8 = 15, вы также сможете делать все эти сложения в уме:
- 70 + 80 это 15 десятков, или 150
- 700 + 800 это 15 сотен, или 1500
- 27 + 8 — это 20, а 15, то есть 35. Или подумайте так: поскольку 7 + 8 на пять больше, чем десять, то 27 + 8 на пять больше, чем следующие десять.
- Вычесть сложением.
Это очень важный принцип, основанный на связи между сложением и вычитанием. Детям действительно не нужно запоминать факты вычитания как таковые, если они могут использовать этот принцип. Например, чтобы найти 8-6, подумайте: «Шесть плюс какое число дает 8?» Другими словами, подумайте о сложении недостающего числа 6 + ___ = 8. Ответ на это также является ответом на 8 — 6.
Этот принцип особенно удобен с вычитаниями, такими как 13-7, 17-8, 16-9 и другими основными фактами вычитания, где уменьшаемое значение находится между 10 и 20.Но вы также можете использовать его во множестве других ситуаций. Например, число 63–52 легче решить сложением: 52 + 11 дает 63, поэтому ответ на 63–52 — 11.
- Пять умноженное на число.
Теперь обратим внимание на умножение. Вот изящный трюк, о котором вы, возможно, не знали. Чтобы найти любое число в 5 раз, сначала умножьте это число на десять, а затем возьмите половину этого числа. Например, 5 × 48 можно найти, умножив 10 × 48 = 480 и взяв половину результата, что дает нам 240.Конечно, вы также можете использовать эту стратегию для таких фактов умножения, как 5 × 7 или 5 × 9.
- Четыре и восемь чисел.
Если вы умеете удваивать числа, значит, это у вас уже есть! Чтобы найти четырехкратное число, удвойте это число дважды. Например, что такое 4 × 59? Сначала найдите удвоение 59, что составляет 118. Затем удвойте это, и вы получите 236.
Точно так же восемь умноженное на число означает просто трижды удвоение. Например, найти 8 × 35 означает удвоить 35, чтобы получить 70, удвоить 70, чтобы получить 140, и (еще раз) удвоить 140, чтобы получить 280.Однако лично я бы преобразовал 8 × 35 в 4 × 70 (вы удваиваете один множитель и делите второй вдвое), что легко решить до 280.
- Умножить на части.
Эта стратегия очень проста и фактически является основой стандартного алгоритма умножения. Вы можете мысленно найти 3 × 74, умножив 3 × 70 и 3 × 4 и сложив результаты. Получаем 210 + 12 = 222. Другой пример: 6 × 218 — это 6 × 200, а 6 × 10 и 6 × 8, что составляет 1200 + 60 + 48 = 1308.
Я надеюсь, что эти небольшие стратегии или принципы вдохновят вас не только на то, чтобы научить своих детей большему количеству мысленных вычислений, но и на их использование в повседневной жизни.Играть с числами никогда не поздно!
Мария Миллер
Статья изначально опубликована на HomeschoolMagazine.com.
Как улучшить свою умственную математику
Боишься ли ты пойти в класс математики ? У вас есть проблемы с числами и школьными предметами, которые включает работа с числами? Если вы ответили утвердительно, вы, вероятно, не большой поклонник математики. Но даже если вы ненавидите предмет , есть несколько приемов, которые вы можете изучить, чтобы улучшить свои математические навыки и упростить задачу .
Многие студенты стремятся улучшить свои умственные математические навыки , чтобы подготовиться к таким предметам в области математики, как геометрия, алгебра, теории, решение уравнений с множественными переменными и многие другие.
Однако многие люди начинают не любить математику, потому что им не нравится с ментальной арифметикой.
Студенты, особенно молодые, ненавидят математику! Многие студенты вынуждены изучать сложение и вычитание в мгновение ока, и, прежде чем они успевают понять концепцию , они спешат через умножение и деление целых чисел .
Вот почему всем настоятельно рекомендуется вернуться к , изучив основы сложения, умножения, деления и извлечения квадратного корня. Свежие в вашей голове навыки действительно могут помочь вам в повседневной жизни .
Имейте в виду, что математика построена на рациональном мышлении , и вы, вероятно, справляетесь с ней лучше, чем думаете. Мы знаем, что вы используете математику, даже не зная простых задач , таких как косметический ремонт комнаты или расчет своего ежемесячного бюджета.
Вы когда-нибудь задавались вопросом, почему вы используете телефонный калькулятор для простого разделения счетов с друзьями в ресторане или для определения скидки при распродаже?
Это как если бы технология забрала у нас способность разбираться во всем в нашей голове . Но так быть не должно! Эти инструменты предназначены для того, чтобы помочь нам, а не для того, чтобы расстроить нас.
Кто угодно может быстро научиться считать . Возьмите уроки элементарной математики прямо сейчас.
Выучить метод сложения тоже можно быстро! (Источник: WonderHowTo)Как можно улучшить математику? Овладение математическими навыками может занять меньше времени, чем вы можете себе представить, и вам не придется записываться на четырехлетний курс с уроком в неделю, чтобы сделать это.
В этой статье мы собрали и поделились некоторыми советами, и приемами , которые помогут вам развить навыки счета и математики. И не волнуйтесь, дело не в том, что изучает , как выполнять сложные вычисления, задачи со словами или снова уравнения . Мы просто показываем, как решать задачи в уме!
Шаг 1. Основы ментальной арифметики
Первое, что вам следует сделать, это забыть о калькуляторе на телефоне, когда пришло время быстро вычислить уравнение, вместо этого воспользуйтесь этими советами, которые помогут вам улучшить умственную арифметику.
Затем вам следует вернуться к таблицам сложения, умножения и деления и заново выучить квадратные корни (до 12 или 15).
Все обучение начинается с основ, даже с математики, так что не верьте ложным объявлениям о сокращении пути к изучению математики.(Источник: TheConversation)Есть несколько методов, которые помогут вам вычислить суммы и таблицы умножения с цифрами от 1 до 9.
Вот несколько математических приемов:
- Чтобы сложить числа, заканчивающиеся на 9, добавьте следующее число, а затем вычтите 1. Например, чтобы вычислить 482+ 39, выполните 482 + 40 = 522 — 1 = 521.
- Тот же процесс, чтобы добавить 11, просто сложите десятки, затем добавьте 1. Например, 725 + 11 = 725 + 10 = 735 + 1 = 736.
- То же самое и с числами, заканчивающимися на 1.Например, 668 + 31 = 668 + 30 = 698 + 1 = 699.
- Чтобы умножить на 4, удвоить число, а затем снова удвоить. Например, 36 x 4 = 36 x 2 x 2 = 72 x 2 = 144.
- Чтобы умножить на 10, вам достаточно добавить 0 в конец числа. Например, 360 x 10 = 3600.
- Когда есть десятичная точка, вам просто нужно переместить десятичную дробь на одну цифру вправо. Например, 52,5 x 10 = 525.
- Чтобы умножить на 100, добавьте 2 нуля в конец числа или переместите десятичный разряд на 2 цифры вправо и т. Д.
- Чтобы умножить на 5, вы можете умножить на 10, а затем разделить на 2. Например, 224 x 5 = 224 x 10/2 = 2240/2 = 1120.
Ментальная практика ведет к совершенству
При постоянном использовании и Правильно, наш мозг способен на невероятно сложные рассуждения. Вот несколько отличных и полезных советов по математике, чтобы использовать возможности нашего мозга .
Имейте в виду, что наш мозг тоже ленив и постоянно ищет возможности выполнять большую часть работы с наименьшими усилиями.Чтобы оставаться впереди игры, вы должны практиковаться!
В современном технологическом обществе все работает и движется на быстрее. То же самое происходит с нашим мозгом, когда речь идет о ментальной арифметике !
Доверьтесь нам, как только вы овладеете арифметикой , вы упростите себе жизнь. Вот несколько забавных уроков математики для ваших детей.
С хорошим репетитором после урока или двух вы будете заниматься математикой, даже не задумываясь! (Источник: IDN Times)Ищите хороших репетиторов по математике , если вам нужна или помощь, чтобы выучить этих рефлексов! Частный репетитор по математике в Атланте может быть именно тем, что прописал доктор.
Репетитор может показать вам, как пользоваться советами и уловками, и помочь вам развить другие навыки, чтобы улучшить вашу умственную арифметику .
Улучшите умственную математику, обновив свой мозг
Каким бы тривиальным ни казалось сравнение вычислений , мозг действительно работает как компьютер.
По данным Института Солка в Ла-Хойя, Калифорния, минимальная емкость нашего мозга составляет около 1000 ГБ. Это эквивалент емкости всего Интернета!
Это означает, что наш мозг является основным элементом, подобным жесткому диску, а наши навыки и знания — это операционные системы . Чтобы он работал лучше, вы должны поддерживать его в актуальном состоянии, как и любую программу computer !
Вы гений математики? Чтобы им стать, в отличие от имиджа, нужно много работать, потому что в жизни нет ничего бесплатного. (Источник: IdleWords)Любой процесс в нашем мозге нуждается в изменениях, чтобы активировать его способности. Чтобы наш мозг работал быстрее, нам нужно много его использовать. Поэтому, чтобы научиться быстро считать как в классе математики, так и в повседневной жизни , требуется много практики.
Вы можете узнать о новых методах улучшения прямо здесь!
Don’t Rush Maths
Помните, когда вы были ребенком, и ваша бабушка говорила вам не «бегать, прежде чем идти»? Вы можете применить к изучению математики. Выберите метод обучения, который вам нравится, и придерживайтесь его. Это значительно упростит изучение математики !
Если вы хотите улучшить ментальную арифметику для игры «Монополия» с друзьями или освободить от необходимости использовать телефон для быстрого вычисления математических задач, вам следует начать медленно, и не торопиться.
Не торопитесь! Спешка обычно приводит к и ошибкам и случайному пропуску важного шага, который может привести к плохой оценке в школе .
Приносит ли математика финансовую грамотность?
Будет не легче, если вы зайдете в Wikihow и найдете статью, чтобы начать изучать некоторые базовые математические навыки. (Источник: CreativINDIE)Имейте в виду, что в математике вы должны начинать медленно, внимательно читать задачу, разбирать каждую задачу шаг за шагом, а вычислить , что вам нужно сделать и как это сделать, чтобы найти ответ.
Лучший способ быстро найти ответ — это попросить помощи у других. Учитель будет знать, как определить проблему и подход , который вам нужно будет использовать.
Не торопитесь, изучая основы арифметики, математических теорий и применяйте их к простым задачам.
Как только вы обретете уверенность, вы можете увеличить на сложность каждого упражнения. Вот как вы продвигаетесь вперед и становитесь лучше.
Развлекайтесь на любом уроке математики
Даже если вы чувствуете себя худшим учеником в классе математики , , вы всегда можете стать лучше в математике, если сосредоточитесь на и приступите к работе!
В нашей повседневной жизни , мы сталкиваемся с ситуациями, когда мы можем использовать математику. Обязательно используйте эти ситуаций в увлекательной игровой форме, чтобы вы могли получить удовольствие от изучения этого предмета.
Вычисление из того, сколько денег у вас осталось после покупки продуктов или вечеринки с друзьями, может быть возможностью создать забавную игру для практики математики.
Еще один способ улучшить свою скорость на уроках математики — это приготовление пищи. Вы можете развить в уме арифметику , пока делаете торт, если вы работаете с с большими числами и переводите единицы измерения (граммы, килограммы, литры и т. Д.).
Как улучшить лучший рецепт? Конечно же, добавить немного математики! (Источник: The Imagination Tree)Вы также будете практиковаться и работать с пропорциональностью и дробями , пока вы придумываете, как разрезать торт для 4 человек на 6 равных частей.
Вы встретите математических единиц в своей жизни чаще, чем вы думаете. Все, что вам нужно сделать, это найти способ развлечься , работая с числами .
Нет тысяч способов улучшить математику, все, что вам нужно, — это тренировать свой ум и практиковаться. Это поможет вам быстрее обращаться с числами и расчетами.
Мозг — это мышца , поэтому о нем нужно заботиться соответственно. Придет время, когда вы даже не поймете, насколько хорошо и быстро вы справились с расчетами . Ученик становится учителем !
Приносит ли школьная математика финансовую грамотность? Узнай!
Стратегии умственного вычитания
Этот урок мысленной математики объясняет 6 различных стратегий, которые вы можете использовать для мысленного вычитания двузначных чисел, предназначенных для 2-го или 3-го класса. Он содержит инструкции, примеры, множество упражнений и текстовых задач, которые студенты должны выполнить.
| Стратегия 1: Вычтем на две части | |||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||
1. Вычтите увеличенное число частями, сначала вычтите до предыдущие целые десять; потом остальное.
|
| ||||||||||||||||
|
| ||||||||||||||||
|
| ||||||||||||||||
|
|
2.Сначала вычтите шары, которые не в десяти группах.
|
|
| Стратегия 2: Используйте известные факты вычитания |
Поскольку 14 — 6 = 8, мы знаем, что ответ на 74 —
6 закончится на 8, Поскольку 15-8 = 7, мы знаем, что
ответ на 55-8 закончится на 7, |
3. Вычесть. Первая проблема в каждой коробке — это «проблема помощи» для других.
а. 14 — 9 = _______ 24 — 9 = _______ 44 — 9 = _______ | г. 17 — 8 = _______ 27 — 8 = _______ 37 — 8 = _______ | г. 12 — 9 = _______ 52 — 9 = _______ 32 — 9 = _______ |
г. 15 — 9 = _______ 65 — 9 = _______ 45 — 9 = _______ | e. 13 — 8 = _______ 33 — 8 = _______ 93 — 8 = _______ | ф. 16-8 = _______ 86 — 8 = _______ 36 — 8 = _______ |
4. а. У Эми 32 доллара. Она
купил комикс за 7 долларов.
Сколько у нее сейчас?
г. Петр имел
29 долларов.Игрушечный поезд, который он хочет, стоит 39 долларов.
Мама платила ему 5 долларов за работу. Как
многое другое
нужно ли теперь Питеру покупать
тренироваться?
г. Цветок
В магазине 55 роз. Восемь из них белые,
а остальные красные. Сколько красных?
| Стратегия 3: Вычесть по частям: десятки и единицы | |||||||||||||||||||||||||||||||||||||||||
| Разбейте вычитаемое число на десятки и единицы.Вычтите по частям. | |||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||
5. Вычесть по частям: второе число разбейте на десятки и единицы.
= __________ |
= __________ |
= __________ | ||||||||||||||||||||||||
г. 69 — 19 | e. 67– 36 | ф. 64 — 33 | ||||||||||||||||||||||||
| Стратегия 4: Доп. | |
Вы можете «добавить назад». Это хорошо работает, если два числа близки друг к другу. Вместо вычитания подумайте, сколько вам нужно добавить к вычитаемому числу (вычитаемое), чтобы получить число, из которого вы вычитаете (уменьшаемое). | |
| 71 — 67 = ?? Думаю: 67+ ____ = 71 | 558 — 556 = ?? Думаю: 556+ ____ = 558 |
6. Вычтите.
а. 78 — 75 = _______ 61 — 58 = _______ | г. 112 — 108 = _______ 692 — 688 = _______ | г. 505 — 499 = _______ 1000 — 994 = _______ |
7.
У вас было 50 долларов. Вы купили два букета роз по 13 долларов каждый.
Сколько у вас осталось после покупки?
8.
Что, если вы купили трех букетов роз по 13 долларов каждый на свои 50 долларов?
Сколько бы у вас осталось после покупки?
9. Пятнадцать
дети играли на детской площадке. Семеро из них ушли.
Затем пришли еще десять детей. Сколько играют на
детская площадка сейчас?
10.Лев преследовал
антилопа на 400 футов, затем еще на 200 футов и
наконец, еще 200 футов. Тогда лев набросился на антилопу.
Какое общее количество футов было у льва?
гнались за антилопой?
| Стратегия 5: Сложите, чтобы найти разницу. | |||||||||||||||||||||
Чтобы найти разницу, начните с меньшего число и складываем , пока не дойдем до большего числа.Ты можно сначала заполнить следующие десять, затем добавить целые десятки, а затем снова добавить единицы.
|
11. Сложите, чтобы найти различия, или используйте другую стратегию, например вычитание по частям.
|
| ||||||||||||||||||||||||||||||||||||||
г. 56 — 28 = _______ 55 — 24 = _______ | г. 72 — 18 = _______ 82 — 46 = _______ | e. 54 — 37 = _______ 91 — 57 = _______ | ф. 74 — 55 = _______ 63 — 34 = _______ |
| Стратегия 6: Вычтите простое число, которое близко, а затем исправьте ответ. | 74 — 39 =? Первое вычитание
74-40 = 34, так как 40 это | 81 — 57 =? Первое вычитание 81-60 = 21, так как
60 — это |
12. Вычтите мысленно.
а. 34 — 18 = ______ 42 — 29 = ______ | г. 65 — 27 = ______ 55 — 38 = ______ | г. 97 — 49 = ______ 62 — 19 = ______ | г. 65 — 29 = ______ 83 — 38 = ______ |
13. Задача на вычитание!
а . 101 — _____ = 92 | г. ________ — 60 = 7 | г. ________ — 132 = 40 |
14. Еще один вызов!
100 | ______ | _____ | _____ | _____ | _____ | _____ | |||||||
Решите загадочные числа
а также
! |

 Поэтому исключается добавление новых учащихся в группу на любом этапе обучения и с любым уровнем знаний.
Поэтому исключается добавление новых учащихся в группу на любом этапе обучения и с любым уровнем знаний.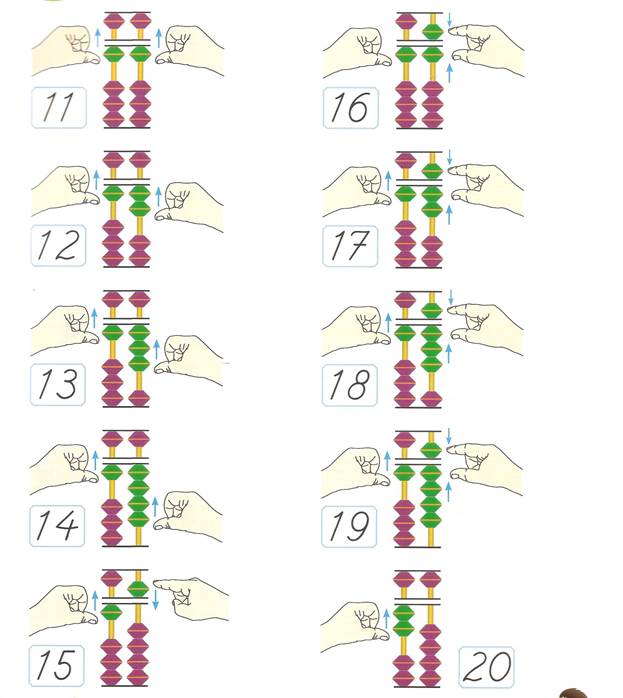
 Методика ISMA так же учит детей считать отрицательные числа, десятичные дроби, корень квадратный, корень кубический , проценты. Вести подсчеты в денежном выражении, в выражении массы и других мерах.
Методика ISMA так же учит детей считать отрицательные числа, десятичные дроби, корень квадратный, корень кубический , проценты. Вести подсчеты в денежном выражении, в выражении массы и других мерах. У детей возникает своего рода конфликт восприятия числа, т.к. школа требует одну систему, в школе ментальной арифметики — другую систему. Отсюда возникает недовольство и негатив у школьных учителей в отношении ментальной арифметики.
У детей возникает своего рода конфликт восприятия числа, т.к. школа требует одну систему, в школе ментальной арифметики — другую систему. Отсюда возникает недовольство и негатив у школьных учителей в отношении ментальной арифметики.