Математика на пальцах для детей: Хитрая таблица умножения на пальцах.Для детей – Мастер-класс «Математика на пальцах»

Мастер-класс «Математика на пальцах»

МАСТЕР — КЛАСС

МАТЕМАТИКА НА ПАЛЬЦАХ

Вам не раз приходилось слышать фразу о том, что математика — страна без границ. Несмотря на свою банальность, она имеет под собой очень веские основания. Позволю утверждать, что математика в жизни человека занимает особое место. Мы настолько срослись с ней, что попросту не замечаем её.

А ведь с математики начинается всё. Ребёнок только родился, а первые цифры в его жизни уже звучат: дата рождения, рост, вес.

Ваш малыш растет, он еще не может выговорить слово «математика», а уже занимается ею, решает небольшие задачи по подсчету игрушек, кубиков. Да и родители о математике не забывают. Готовя ребенку пищу, взвешивая его, вы решаете элементарные задачи: сколько еды нужно приготовить для малыша, учитывая его вес.

Не успели оглянуться, он — уже школьник! Вот здесь и начинаются первые трудности в учебе. Признаемся себе, что у многих самым нелюбимым предметом в школе была математика. И ничего удивительного в этом нет. Вы любите заниматься тем, что у вас не получается? Вопрос не риторический. Дело в том, что детишки, которые не в ладах с математикой чаще всего жалуются на то, что они ничего не понимают в этих «дурацких задачах» и этих «длиннющих как удавы» примерах. Сложно полюбить то, чего не понимаешь, правда? Тем не менее, требования для всех учеников школы таковы, что хочешь — не хочешь, любишь — не любишь, а решать, считать, запоминать теоремы все равно придется.

Все родители учеников начальной школы рано или поздно сталкиваются с вопросом, как помочь своему ребенку выучить таблицу умножения. Ведь таблица умножения — это те необходимые знания, которые требуются человеку в любом возрасте, это залог успеха в дальнейшей учебе. Но психологами доказано, что выучить всю таблицу наизусть могут не все дети. Мы, учителя математики знаем, что и среди школьников средних и даже старших классов имеется достаточное количество детей, плохо знающих таблицу умножения.

Вот в школах Монтессори знакомство с цифрами и арифметическими действиями – это интересная и весёлая игра, в ходе которой ребёнок и рисует, и фантазирует, и мир познаёт, и с камушками да палочками возится, а ещё слушает сказку о четырёх дружных братцах – Умножении, Делении, Минусе и Плюсе! Как же иначе?! Ведь в начальных классах реальностью для детей является не точное научное понятие, а художественный образ. И для запоминания таблицы умножения существует немало способов — в стихах, картинках, играх. Я предлагаю вам показать своему ребенку еще один интересный способ — таблицу умножения на пальцах.

Для детей младшего школьного возраста с преобладающим кинестезическим восприятием и кинестезической памятью прием пальцевого счета при освоении таблицы умножения может быть рекомендован как вспомогательный. Для того

чтобы его эффективно использовать, следует знать результаты табличного умножения в пределах таблицы умножения числа 4.

Например, нужно умножить 6 на 7. Зажимаем пальцы на обеих руках в кулак, а затем на каждой руке отгибаем столько пальцев, насколько каждый множитель больше, чем пять. На двух руках отогнуто три пальца — это число десятков в искомом числе. На одной руке остались прижатыми к ладони три пальца, на другой — четыре пальца, эти числа перемножаем 3 * 4 = 12 и прибавляем к числу, имеющихся десятков. 30 + 12 = 42. Ответ: 6 * 7 = 42.

А теперь попробуйте самостоятельно умножить этим способом 8 на 9.

Отгибаем на одной руке три пальца, а на другой руке — четыре пальца (на столько каждый множитель больше, чем пять). Отогнуто 7 пальцев — это десятки в искомом числе. Перемножаем число загнутых пальцев обеих рук: 2 * 1 = 2. Прибавляем это количество к числу десятков 70 + 2 = 72. Таким образом, 9 * 8 = 72.

Еще проще метод умножения на 9. Итак, всё, что вам понадобится — это десять пальцев рук. Положите ладони на стол. Мысленно дайте каждому пальцу, начиная от мизинца левой руки и заканчивая мизинцем правой, свой номер от 1 до 10.

Вот так: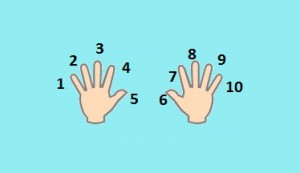

Допустим, нам надо умножить 3 на 9. Чтобы вычислить ответ, надо найти палец под номером 3 и поднять его. А затем посмотреть, сколько пальцев осталось лежать справа и слева. Количество пальцев слева от поднятого пальца (в нашем случае их 2) — это десятки, количество пальцев справа (у нас это 7) — это единицы. Итого, получаем — 2 и 7, то есть 27.

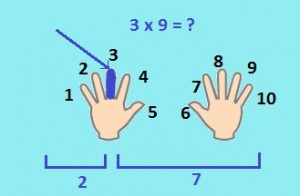
Метод умножения на 11. Например: 23*11.

Первая цифра 2, третья цифра 3, посередине сумма 2+3=5.Получается 253. Следующий пример 67*11=737. Посередине 6+7=13, поэтому к первой цифре прибавили 1, будет 7.

Метод умножения на 15. Например: 22*15. Сначала

22 *10=220. Затем прибавляем половину числа 220, это 110. получается: 22*15= 220+110=330.

В 9 классе ученики начинают изучать тригонометрию. Синусы, косинусы, тангенсы, котангенсы. Ученики с трудом запоминают эту тему.

А оказывается, значения синусов и косинусов углов «находятся» на вашей ладони. Протяните руку (любую) и разведите как можно сильнее пальцы (как на слайде). Оказывается между мизинцем и большим пальцем угол 90, между мизинцем и безымянным – 30, между мизинцем и средним – 45, между мизинцем и указательным – 60. И это у всех людей без исключения

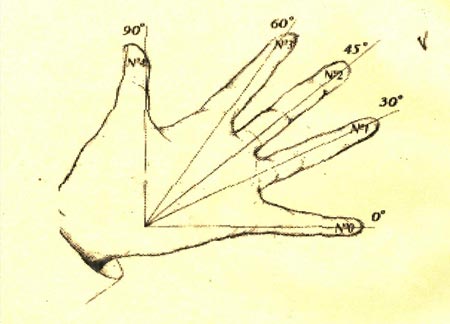
Введем нумерацию пальцев:

мизинец № 0 – соответствует 0,
безымянный № 1 – соответствует 30,
средний № 2 – соответствует 45,
указательный № 3 – соответствует 60,
большой № 4 – соответствует 90.

Остается только запомнить формулу.

n – номер пальца

Угол

Значение

0

0

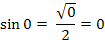
1

30

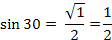
2

45

3

60

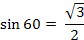
4

90

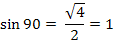
Конечно, значения sin α или cos α надо знать наизусть, но вдруг это правило поможет в трудную минуту.

А еще для запоминания значений синуса и косинуса для углов в 30º, 45º и 60º я предлагаю своим ученикам небольшую сказку.

– Пошли три дамы гулять. Первая дама, вторая дама и третья дама. И неожиданно пошел дождь. Все дамы открыли зонтики, и одели по паре калош. Прогулка была закончена, и дамы вернулись домой. Первая дама, вторая дама и третья дама пошли домой. (Сначала, в таблице, во второй строке по порядку указываются номера дам. За тем изображают корни – “зонтики”, и “надевают калоши” – в знаменателях пишут 2).

Незаметно бежит время. И вот уже выпускной класс. Пора сдавать ЕГЭ. Все хотят хорошо сдать ЕГЭ по математике. Тогда вам просто необходимо уметь считать быстро, правильно и без калькулятора. Ведь главная причина потери баллов на ЕГЭ по математике – вычислительные ошибки.

По правилам проведения ЕГЭ, пользоваться калькулятором на экзамене по математике не разрешено. На самом деле калькулятор на ЕГЭ по математике не нужен. Все задачи решаются без него. Главное – внимание, аккуратность и некоторые секретные приемы, о которых я сейчас расскажу.

Квадратные уравнения встречаются нам в задачах В5, В12 и В13 вариантов ЕГЭ, а также в части С. В них нужно считать дискриминант, а затем извлекать из него корень.

Но не торопитесь. Если какое-то вычисление можно упростить – упростите его.

Вот, например, такое «дьявольское уравнение»:

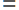666²  999  666  0

Семьдесят процентов выпускников решают его «в лоб». Считают дискриминант по формуле b²  4ac, после чего говорят, что корень невозможно извлечь без калькулятора. Но ведь можно разделить левую и правую части уравнения на 333. Получится 

2²  3  2 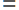 0 Какой способ проще?

Иногда дискриминант удается посчитать по известной формуле сокращенного умножения: a² 

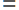 b²  (ab)(ab). Вот, например, такое уравнение вполне может получиться при решении задачи В12:

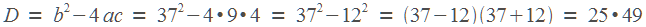
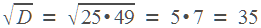
Применим эту формулу для решения задачи В4.

Гипотенуза прямоугольного треугольника равна 39, один из катетов равен 36, найти второй катет.

По теореме Пифагора, он равен 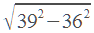. Можно долго считать в столбик, но проще применить формулу сокращенного умножения.

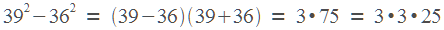
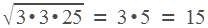
Легко запомнить, что числа, оканчивающиеся на 5, в квадрат возводятся моментально.

Допустим, надо найти квадрат числа А5 (А — не обязательно цифра, любое натуральное число). Умножаем А на А+1 и к результату приписываем 25. Всё!

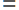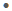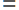Например: 45²  2025   (4  5  20 и приписали 25).

65² 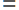 4225   (6  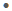7 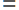 42 и приписали 25).

125² 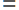 15625   (12  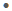13 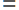 156 и приписали 25).

Проверка заданий части В  – автоматическая. Здесь не бывает «почти правильного» ответа. Либо он правилен, либо нет. Одна вычислительная ошибка – и привет, задача не засчитывается. Поэтому необходимо научить учеников считать быстро, правильно и без калькулятора.

Школа осталась позади. Казалось бы, что после школы математика нигде не пригодится. Увы! Тут приходится использовать математику ещё чаще. Во время учёбы в вузе, на работе и дома нужно постоянно решать задачи, и не только математические. Какова вероятность успешной сдачи экзамена по математике? Сколько денег нужно заработать, чтобы купить квартиру? Каким должен быть объём вашего дома и сколько для этого нужно приобрести кирпича. Как правильно рассчитать, чтобы родилась девочка или мальчик? И тут на помощь придёт математика. Она следует за человеком везде, помогает ему решать задачи, делает его жизнь намного удобнее.

Покупая газировку, конфеты, или кофе, вы, разумеется, видели на упаковке наклейку с полосками и цифрами. Что бы это значило?

Это не что иное как ШТРИХ КОД. С помощью него зашифрована информация о некоторых наиболее существенных параметрах продукции.

Большинство производителей придерживаются установленной системы кодирования. И не надо быть семи пядей во лбу, чтобы загадку эту разгадать, потому что каждая цифра обозначает конкретные данные.

Согласно этой системе, каждому виду изделия присваивается свой номер состоящий чаще всего из 13 цифр:

• Первые две – код страны

• Последующие 5 – код изготовителя

• Еще 5 наименование товара

• И последняя – знак товара или контрольная цифра;

В последнее время очень много нелегальных производств подпольной продукции, но как же простому покупателю отличить где подделка, а где настоящий товар?? Именно в этом нам и поможет МАТЕМАТИКА. Каждый кто хорошо умеет считать может без особых усилий раскрыть тайну магических цифр.

Если проделать несложные арифметические вычисления с цифрами штрих-кода, есть шанс доподлинно узнать о том, настоящий продукт перед вами или банальная подделка. Вот эта формула: Сложите цифры, стоящие на четных местах. Полученную сумму умножьте на три. Сложите цифры, стоящие на нечетных местах, кроме последней. Сложите два предыдущих результата. А теперь от этой суммы отбросьте первую цифру. Из десяти вычтите последний получившийся результат. И радуйтесь — вычисления можно закончить. Если у вас получилась цифра, равная последней, контрольной, значит перед вами оригинальный продукт. Если цифры не совпадают, перед вами, скорее всего, подделка.

Можно ли проверить подлинность купюры евро по серийному номеру?
Подлинность единой европейской валюты можно проверить по ее серийному номеру. Букву нужно заменить на ее порядковый номер в английском алфавите и сложить с остальными цифрами, затем у получившегося числа сложить все цифры и т.д. до тех пор пока не останется одна цифра. Если эта цифра не равна 8, то купюра фальшивая.

Стремительно изменяется мир и сама жизнь. В неё входят новые технологии. Только математика и решение задач в традиционном понимании не изменяют себе. Математические законы проверены и систематизированы, поэтому человек в важные моменты может положиться на неё, решить любую задачу. Математика не подведёт.

Свой мастер – класс мне хотелось бы закончить, перефразируя высказывание Гете: «Часто говорят, что цифры управляют миром; по крайней мере, надеюсь, что мой мастер – класс вас убедил в том, что цифры показывают, как он управляется»

Математика на пальцах

МАСТЕР — КЛАСС

МАТЕМАТИКА НА ПАЛЬЦАХ

Признаемся себе, что у многих самым нелюбимым предметом в школе была математика. И ничего удивительного в этом нет. Вы любите заниматься тем, что у вас не получается? Вопрос не риторический. Дело в том, что дети, которые не в ладах с математикой чаще всего жалуются на то, что они ничего не понимают в этих «дурацких задачах» и этих «длиннющих как удавы» примерах. Сложно полюбить то, чего не понимаешь, правда? Тем не менее, требования для всех учеников школы таковы, что хочешь — не хочешь, любишь — не любишь, а решать, считать, запоминать теоремы все равно придется.

Все родители учеников начальной школы рано или поздно сталкиваются с вопросом, как помочь своему ребенку выучить таблицу умножения. Ведь таблица умножения — это те необходимые знания, которые требуются человеку в любом возрасте, это залог успеха в дальнейшей учебе. Но психологами доказано, что выучить всю таблицу наизусть могут не все дети. Мы, учителя математики знаем, что и среди школьников средних и даже старших классов имеется достаточное количество детей, плохо знающих таблицу умножения.

Для запоминания таблицы умножения существует немало способов — в стихах, картинках, играх. Я сейчас вампокажу один интересный способ — таблицу умножения на пальцах.

Для детей младшего школьного возраста с преобладающим кинестезическим восприятием и кинестезической памятью прием пальцевого счета при освоении таблицы умножения может быть рекомендован как вспомогательный. Для того чтобы его эффективно использовать, следует знать результаты табличного умножения в пределах таблицы умножения числа 4. Например, нужно умножить 6 на 7. Зажимаем пальцы на обеих руках в кулак, а затем на каждой руке отгибаем столько пальцев, насколько каждый множитель больше, чем пять. На двух руках отогнуто три пальца — это число десятков в искомом числе. На одной руке остались прижатыми к ладони три пальца, на другой — четыре пальца, эти числа перемножаем 3 * 4 = 12 и прибавляем к числу, имеющихся десятков. 30 + 12 = 42. Ответ: 6 * 7 = 42.

А теперь попробуйте самостоятельно умножить этим способом 8 на 9.

Отгибаем на одной руке три пальца, а на другой руке — четыре пальца (на столько каждый множитель больше, чем пять). Отогнуто 7 пальцев — это десятки в искомом числе. Перемножаем число загнутых пальцев обеих рук: 2 * 1 = 2. Прибавляем это количество к числу десятков 70 + 2 = 72. Таким образом, 9 * 8 = 72.

Еще проще метод умножения на 9. Итак, всё, что вам понадобится — это десять пальцев рук. Положите ладони на стол. Мысленно дайте каждому пальцу, начиная от мизинца левой руки и заканчивая мизинцем правой, свой номер от 1 до 10.

Вот так:

Допустим, нам надо умножить 3 на 9. Чтобы вычислить ответ, надо найти палец под номером 3 и поднять его. А затем посмотреть, сколько пальцев осталось лежать справа и слева. Количество пальцев слева от поднятого пальца (в нашем случае их 2) — это десятки, количество пальцев справа (у нас это 7) — это единицы. Итого, получаем — 2 и 7, то есть 27.

В 9 классе ученики начинают изучать тригонометрию. Синусы, косинусы, тангенсы, котангенсы. Ученики с трудом запоминают эту тему.

А оказывается, значения синусов и косинусов углов «находятся» на вашей ладони. Протяните руку (любую) и разведите как можно сильнее пальцы (как на слайде). Оказывается между мизинцем и большим пальцем угол 90, между мизинцем и безымянным – 30, между мизинцем и средним – 45, между мизинцем и указательным – 60. И это у всех людей без исключения

Введем нумерацию пальцев:

мизинец № 0 – соответствует 0,
безымянный № 1 – соответствует 30,
средний № 2 – соответствует 45,
указательный № 3 – соответствует 60,
большой № 4 – соответствует 90.

Остается только запомнить формулу.

, n – номер пальца

№ пальца	Угол	Значение
0	0
1	30
2	45
3	60
4	90

Конечно, значения sin α или cos α надо знать наизусть, но вдруг это правило поможет в трудную минуту.

А еще для запоминания значений синуса и косинуса для углов в 30º, 45º и 60º я предлагаю своим ученикам небольшую сказку.

– Пошли три дамы гулять. Первая дама, вторая дама и третья дама. И неожиданно пошел дождь. Все дамы открыли зонтики, и надели по паре калош. Прогулка была закончена, и дамы вернулись домой. Первая дама, вторая дама и третья дама пошли домой. (Сначала, в таблице, во второй строке по порядку указываются номера дам. За тем изображают корни – “зонтики”, и “надевают калоши” – в знаменателях пишут 2).

Незаметно бежит время. И вот уже выпускной класс. Пора сдавать ЕГЭ. Все хотят хорошо сдать ЕГЭ по математике. Тогда вам просто необходимо уметь считать быстро, правильно и без калькулятора. Ведь главная причина потери баллов на ЕГЭ по математике – вычислительные ошибки.

По правилам проведения ЕГЭ, пользоваться калькулятором на экзамене по математике не разрешено. На самом деле калькулятор на ЕГЭ по математике не нужен. Все задачи решаются без него. Главное – внимание, аккуратность и некоторые секретные приемы, о которых я сейчас расскажу.

Легко запомнить, что числа, оканчивающиеся на 5, в квадрат возводятся моментально.

Допустим, надо найти квадрат числа А5 (А — не обязательно цифра, любое натуральное число). Умножаем А на А+1 и к результату приписываем 25. Всё!

Например: 45²  2025   (4  5  20 и приписали 25).

65²  4225   (6  7  42 и приписали 25).

125²  15625   (12  13  156 и приписали 25).

Проверка заданий части В  – автоматическая. Здесь не бывает «почти правильного» ответа. Либо он правилен, либо нет. Одна вычислительная ошибка – и привет, задача не засчитывается. Поэтому необходимо научить учеников считать быстро, правильно и без калькулятора.

Школа осталась позади. Казалось бы, что после школы математика нигде не пригодится. Увы! Тут приходится использовать математику ещё чаще. Какова вероятность успешной сдачи экзамена по математике? Сколько денег нужно заработать, чтобы купить квартиру? Каким должен быть объём вашего дома и сколько для этого нужно приобрести кирпича.

Покупая газировку, конфеты, или кофе, вы, разумеется, видели на упаковке наклейку с полосками и цифрами. Что бы это значило?

Это не что иное как ШТРИХ КОД. С помощью него зашифрована информация о некоторых наиболее существенных параметрах продукции.

Большинство производителей придерживаются установленной системы кодирования. И не надо быть семи пядей во лбу, чтобы загадку эту разгадать, потому что каждая цифра обозначает конкретные данные.

Согласно этой системе, каждому виду изделия присваивается свой номер состоящий чаще всего из 13 цифр:

• Первые две – код страны

• Последующие 5 – код изготовителя

• Еще 5 наименование товара

• И последняя – знак товара или контрольная цифра;

В последнее время очень много нелегальных производств подпольной продукции, но как же простому покупателю отличить где подделка, а где настоящий товар?? Именно в этом нам и поможет МАТЕМАТИКА. Каждый кто хорошо умеет считать может без особых усилий раскрыть тайну магических цифр.

Если проделать несложные арифметические вычисления с цифрами штрих-кода, есть шанс доподлинно узнать о том, настоящий продукт перед вами или банальная подделка. Вот эта формула: Сложите цифры, стоящие на четных местах. Полученную сумму умножьте на три. Сложите цифры, стоящие на нечетных местах, кроме последней. Сложите два предыдущих результата. А теперь от этой суммы отбросьте первую цифру. Из десяти вычтите последний получившийся результат. И радуйтесь — вычисления можно закончить. Если у вас получилась цифра, равная последней, контрольной, значит перед вами оригинальный продукт. Если цифры не совпадают, перед вами, скорее всего, подделка.

Можно ли проверить подлинность купюры евро по серийному номеру?

Подлинность единой европейской валюты можно проверить по ее серийному номеру. Букву нужно заменить на ее порядковый номер в английском алфавите и сложить с остальными цифрами, затем у получившегося числа сложить все цифры и т.д. до тех пор пока не останется одна цифра. Если эта цифра не равна 8, то купюра фальшивая.

Стремительно изменяется мир и сама жизнь. В неё входят новые технологии. Только математика и решение задач в традиционном понимании не изменяют себе. Математические законы проверены и систематизированы, поэтому человек в важные моменты может положиться на неё, решить любую задачу. Математика не подведёт.

Свой мастер – класс мне хотелось бы закончить, перефразируя высказывание Гётте: «Часто говорят, что цифры управляют миром; по крайней мере, надеюсь, что мой мастер – класс вас убедил в том, что цифры показывают, как он управляется»

Математика: умножение на пальцах

Если ребенку никак не удается выучить таблицу умножения, расскажите ему о маленьких хитростях, которые помогут решать школьные задачки и примеры без проблем! Самый легкий способ справиться с умножением – это умножение на пальцах.

Да-да, на пальцах можно не только считать, но и умножать. И если таблица умножения на 1, 2, 3, 4 и 5, как правило, дается ребенку без труда, то для того, чтобы научиться умножать на 6, 7, 8, и 9 ему понадобится ваша помощь. Умножение на пальцах рук поможет ребенку делать домашние задания по математике без труда.

Читай также: Как преодолеть страх перед математикой

Умножение на пальцах 6, 7 и 8

Умножение на пальцах рук на 6, 7, 8

Поверните кисти рук ладонями к себе. Каждому пальцу, начиная с мизинца, присвойте цифры от 6 до 10.

Теперь таким же образом попробуйте умножить 7 на 8. Для этого соедините палец №7 на левой руке с пальцем №8 на правой.

Таблица умножения: умножение на пальцах

Теперь сосчитайте пальцы: количество пальцев под соединенными пальцами – это десятки.

Таблица умножения: умножение на пальцах

Таблица умножения: умножение на пальцах

Пальцы левой руки, оставшиеся сверху, умножьте на пальцы правой руки – это и будут единицы (3 х 2=6). Итог равен 56.

Если при умножении “единиц” результат получается больше 9, то оба результата нужно плюсовать в столбик.

Например, если нужно 7 умножить на 6.

В этом случае “единицы” равны 12 (3 х 4). А десятки равны 3.

3 (десятки)
+
12 (единицы)
________
42

Умножение на пальцах на 9

Поверните кисти ладонями к себе. Теперь нумерация пальцев будет идти по порядку, с лева на право, то есть от 1 до 10, как на рисунке.

Таблица умножения: умножение на пальцах

Попробуйте умножить 2 на 9. Все то, что идет до пальца №2 – это десятки (то есть 1 в этом случае). А все то, что остается после пальца №2 – единицы (то есть 8). В итоге получаем 18.

Источник: instructables.com

Как быстро выучить таблицу умножения на 9 (ВИДЕО)

Если вы знаете легкий способ выучить таблицу умножения, поделитесь им с другими мамами и детьми на нашем форуме.

Читай также: Нужно ли помогать ребенку с домашним заданием

Читай также: Читаем и завидуем: как проходят уроки физкультуры в канадских школах

Читай также: 10 типов родителей, которых учителя тайно ненавидят

Картотека по математике (средняя группа) на тему: Математика на пальцах

Считаем на пальцах,
или
Математика для крошек

(веселые, но необходимые инструкции для родителей и воспитателей)

Потягунюшки,
порастунюшки,
Поперек себя толстунюшки!
Ручки — хватунюшки,
Ножки — ходунюшки,
Роток — говорок!*

Старая-престарая приговорка. С помощью этих смешных словечек мама или бабушка могут приголубить малыша, показать, как любима каждая частичка его маленького тельца. И пусть оно растет здоровым, красивым и ловким. Но тем, что руки — «хватунюшки», а ноги — «ходунюшки», их функции еще не исчерпываются. В жизни ребенка его тело играет роль первого обучающего пособия ПО МАТЕМАТИКЕ.

Тело ребенка — универсальные счеты, лучше всех наглядных пособий, лучше картинок и таблиц. Прежде чем считать предметы, малыш (с вашей помощью) «обнаруживает» себя: вот Я какой! Вот как Я устроен!

А вам-то как интересно каждый раз при раздевании, одевании, купании посчитать, сколько у сынишки (или у дочурки) маленьких носов!

Один нос (носик, носишко). Этот любопытный нос можно потрогать и даже осторожно «попикать» им, как кнопочкой.

А ртов сколько? Столько же, сколько носов, — тоже один. Даже у крокодила зубастого — и то один рот. У девочек и мальчиков больше одного рта не бывает. Они же не многоголовые драконы!

А вот глаза (глазки, глазоньки, глазочки). Сколько их? Два. Два братца через мостик живут, друг друга не видят. Зато малыш все видит. И у мамы два глаза, и у папы. Люди заглядывают друг другу в глаза, как в окошки волшебного домика: хорошо ли там? Тепло ли? Что там живет — доброе или злое, грустное или веселое? А когда мы засыпаем, свет в окошках гаснет…

Только в древних историях — мифах — бывают страшные великаны Циклопы, у которых всего один глаз в середине лба. И в сказке про Крошечку-Хаврошечку у злой мачехиной дочки было три глаза. Поэтому ее называли Трехглазка. Ее третий глаз все высматривал да подглядывал. Не простой глаз — колдовской…

И так далее: два плеча, два локтя, две руки, две ноги, две коленки, два уха, две дырочки-ноздри в носу, две щеки… Даже… (тсс!.. никто не подслушивает?) — даже попка из двух половинок сделана!

И вот ваш малыш вместе с вами весело считает до двух и ощущает это «два» всем собой, всем своим маленьким, любимым вами тельцем.

Но настоящий счет начинается тогда, когда в поле зрения ребенка попадает рука с ее пятью пальцами.

Пальцы обладают замечательными способностями: кроме того, что ими можно трогать, брать, держать, с ними еще и играть можно!

Для начала (хотя это совсем не обязательно) неплохо нарисовать на подушечках пальцев веселые рожицы. Тогда пальцы сразу превращаются в маленьких человечков, которые чего только не умеют!

Например, «плясать» под разные приговорки.

Иногда так:

Вот как пляшет наш Большак:
И вот эдак, и вот так!
Он один впереди,
А четыре позади.
Все четыре позади —
Он один впереди*.

Иногда так:

Пять маленьких леди пошли погулять,
В пути они стали громко болтать.
(Это шевелятся пальцы левой руки.)
Пять джентльменов их услыхали,
С ними всю ночь напролет танцевали.
(Тут «выскакивают» пальцы правой руки и «встречаются» с пальцами левой: большой — с большим, указательный — с указательным, средний — со средним и т.д.)
Польку, кадриль, менуэт и гавот,
Танго, и румбу, и вальс, и фокстрот!

(Подушечки пальцев касаются друг друга поочередно. А после танца «леди» и «джентльмены» «благодарят» друг друга: каждая пара по очереди «кланяется» партнеру.)

С пальцами можно играть в прятки. Так:

На лужайке пять зайчат
Веселятся и пищат.
Как лисицу увидали,
Так четыре убежали.

(Четыре пальца прячутся в кулачок.)

Или так:

На полянке пять бельчат
Веселятся и пищат.
Как куницу увидали,
Три бельчонка убежали.

(Три пальца прячутся в кулачок.)

Можно так:

На опушке пять волчат
Веселятся и рычат.
Как собаку увидали,
Двое сразу убежали.

Играем до тех пор, пока не истощатся время и фантазия или игра, наконец, не надоест.
Пальцы очень полезно заставлять работать «счетами», давая им такие задания:
— Покажи мне два пальца! А еще как можно? А еще?

С двумя-то пальцами легко справиться, а вот с четырьмя (это четыре пальца подряд; два — на левой и два — на правой; три — на правой и один — на левой и т.д.) уже нужно серьезно трудиться. И пальцы не всегда слушаются, и вариантов много.

Вам смешно, когда малыш, будучи совсем крошечным, пытается засунуть в рот большой палец ноги. Кажется, будто он перепутал ногу с рукой. Как маленькая обезьянка. Но вот он встает на ножки, делает первые шаги… С этого момента ступни оказываются плотно упакованными в ботиночки. Им твердо указывается их роль — ходить!

Не поленитесь время от времени «разоблачать» ножки ребенка, чтобы задать им и другую полезную работу.

С давних времен известно, что в ступне человека много активных точек, делающих ее чувствительной к температурным раздражителям. Поэтому часто советуют начинать закалку с обливания ног и с хождения босиком. Кроме того, босоногая ступня, как и рука, соприкасаясь с разного рода поверхностями — гладкими, шершавыми, холодными, мягкими и т.д., — является «добытчиком» новых для человека осязательных впечатлений. Поэтому маленькие коврики из разных материалов и разной фактуры могут сослужить в развитии ребенка не меньшую службу, чем, например, пособия Монтессори, служащие этой цели, но имеющие в виду работу рукой. Как только вы разули малыша и предложили ему занятие на ковриках, вы убиваете сразу трех зайцев: зайца закалки, зайца по профилактике плоскостопия (бич городских детей) и зайца развития (ребенок обучается различать материалы и запоминает новые слова).

Делать пальчиковую гимнастику для ног не менее полезно, как и для рук. И на ногах есть Большак, который не прочь потанцевать время от времени. Чтобы предоставить ему такую возможность, надо сесть на коврик и вытянуть ножки вперед.

Помахали правой ножкой,
Что скакала по дорожке.
Помахали левой ножкой,
Что скакала по дорожке.
Пальчиков на правой — пять,
(Шевелим пальцами правой ноги)
Пальчиков на левой — пять.
(Шевелим пальцами левой ноги)
Было пять,
Осталось пять,
Сосчитаем их опять!

Еще пальцы на ногах можно разводить как можно шире, а потом с силой поджимать:

Старик Егор
Срубил забор.
В заборе дыра.
В дыру лезет вор!

На последних словах ноги нужно быстро поджать под себя или поднять в воздух, потому что у деда Егора есть большой сторожевой пес. И этот пес собирается больно укусить воришку. А в рифмовке такое количество звуков Р, что можно вполне соединить пальчиковые игры с логопедической тренировкой.

Еще ступнями можно хлопать, как в ладоши. Сидим на полу, болтаем ногами:

Как под пальмой на полянке
Жили-были обезьянки.
Трали-вали — топ-топ-топ
(Топаем ступнями по полу),
Трали-вали — хлоп да хлоп!
(«Хлопаем» ступнями ног)

Конечно, возможностей у пальцев ног меньше и их не нужно тренировать так же серьезно, как пальцы руки: в конце концов в школе им писать не придется!
Но дома… Почему бы не попробовать дома рисовать и писать ногами?
Возможно, «из-под ноги» вашего малыша выйдет некий шедевр таинственно-абстракционистского толка, и вы не погнушаетесь повесить его на стенку.

Марина АРОМШТАМ
(отрывок из книги «Дом, в котором живет Малыш»)

* Потешки, отмеченные звездочками, являются фольклорными текстами. Остальные рифмовки принадлежат автору.

Презентация и разработка по теме :»Математика на пальцах»

Хасанова Хеда Шарудиевна

МБОУ «СОШ с.Чишки»

учитель математики

МАСТЕР — КЛАСС

МАТЕМАТИКА НА ПАЛЬЦАХ

Вам не раз приходилось слышать фразу о том, что математика — страна без границ. Несмотря на свою банальность, она имеет под собой очень веские основания. Позволю утверждать, что математика в жизни человека занимает особое место. Мы настолько срослись с ней, что попросту не замечаем её.

А ведь с математики начинается всё. Ребёнок только родился, а первые цифры в его жизни уже звучат: дата рождения, рост, вес.

Признаемся себе, что у многих самым нелюбимым предметом в школе была математика. И ничего удивительного в этом нет. Вы любите заниматься тем, что у вас не получается? Вопрос не риторический. Дело в том, что детишки, которые не в ладах с математикой чаще всего жалуются на то, что они ничего не понимают в этих «дурацких задачах» и этих «длиннющих как удавы» примерах. Сложно полюбить то, чего не понимаешь, правда? Тем не менее, требования для всех учеников школы таковы, что хочешь — не хочешь, любишь — не любишь, а решать, считать, запоминать теоремы все равно придется.

Рано или поздно мы сталкиваемся с вопросом, как помочь своему ребенку выучить таблицу умножения. Ведь таблица умножения — это те необходимые знания, которые требуются человеку в любом возрасте, это залог успеха в дальнейшей учебе. Но психологами доказано, что выучить всю таблицу наизусть могут не все дети. Мы, учителя математики знаем, что и среди школьников средних и даже старших классов имеется достаточное количество детей, плохо знающих таблицу умножения.

Вот в школах Монтессори знакомство с цифрами и арифметическими действиями – это интересная и весёлая игра, в ходе которой ребёнок и рисует, и фантазирует, и мир познаёт, и с камушками да палочками возится, а ещё слушает сказку о четырёх дружных братцах – Умножении, Делении, Минусе и Плюсе! Как же иначе?! Ведь в начальных классах реальностью для детей является не точное научное понятие, а художественный образ. И для запоминания таблицы умножения существует немало способов — в стихах, картинках, играх. Я предлагаю вам показать своему ребенку еще один интересный способ — таблицу умножения на пальцах.

Для тогочтобы его эффективно использовать этот способ, следует знать результаты табличного умножения в пределах таблицы умножения числа 4. Например, нужно умножить 6 на 7. Зажимаем пальцы на обеих руках в кулак, а затем на каждой руке отгибаем столько пальцев, насколько каждый множитель больше, чем пять. На двух руках отогнуто три пальца — это число десятков в искомом числе. На одной руке остались прижатыми к ладони три пальца, на другой — четыре пальца, эти числа перемножаем 3 * 4 = 12 и прибавляем к числу, имеющихся десятков. 30 + 12 = 42. Ответ: 6 * 7 = 42.

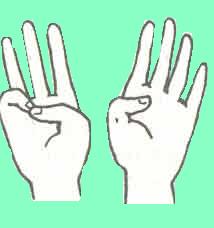
А теперь попробуйте самостоятельно умножить этим способом 8 на 9.

Отгибаем на одной руке три пальца, а на другой руке — четыре пальца (на столько каждый множитель больше, чем пять). Отогнуто 7 пальцев — это десятки в искомом числе. Перемножаем число загнутых пальцев обеих рук: 2 * 1 = 2. Прибавляем это количество к числу десятков 70 + 2 = 72. Таким образом, 9 * 8 = 72.

Еще проще метод умножения на 9. Итак, всё, что вам понадобится — это десять пальцев рук. Положите ладони на стол. Мысленно дайте каждому пальцу, начиная от мизинца левой руки и заканчивая мизинцем правой, свой номер от 1 до 10.

Вот так: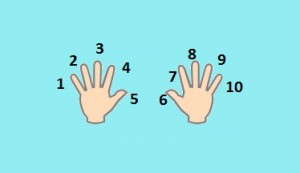

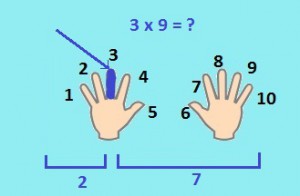
Допустим, нам надо умножить 3 на 9. Чтобы вычислить ответ, надо найти палец под номером 3 и поднять его. А затем посмотреть, сколько пальцев осталось лежать справа и слева. Количество пальцев слева от поднятого пальца (в нашем случае их 2) — это десятки, количество пальцев справа (у нас это 7) — это единицы. Итого, получаем — 2 и 7, то есть 27.

В 9 классе ученики начинают изучать тригонометрию. Синусы, косинусы, тангенсы, котангенсы. Ученики с трудом запоминают эту тему.

А оказывается, значения синусов и косинусов углов «находятся» на вашей ладони. Протяните руку (любую) и разведите как можно сильнее пальцы (как на слайде). Оказывается между мизинцем и большим пальцем угол 90, между мизинцем и безымянным – 30, между мизинцем и средним – 45, между мизинцем и указательным – 60. И это у всех людей без исключения

Введем нумерацию пальцев:

мизинец № 0 – соответствует 0,
безымянный № 1 – соответствует 30,
средний № 2 – соответствует 45,
указательный № 3 – соответствует 60,
большой № 4 – соответствует 90.

Остается только запомнить формулу.

№ пальца

Угол

Значение

0

0

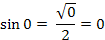
1

30

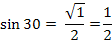
2

45

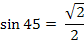
3

60

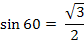
4

90

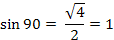
Конечно, значения sin α или cos α надо знать наизусть, но вдруг это правило поможет в трудную минуту.

Математика на пальцах — Тайная нора — LiveJournal

? LiveJournal

• Find more
  • Communities
  • RSS Reader
• Shop
• Help

Login

• Login
• CREATE BLOG Join
• English (en)
  • English (en)
  • Русский (ru)
  • Українська (uk)
  • Français (fr)
  • Português (pt)
  • español (es)
  • Deutsch (de)
  • Italiano (it)
  • Беларуская (be)

Таблица умножения на 6, 7, 8 и 9 на пальцах

Если моя память мне не изменяет, таблица умножения до 5 включительно далась достаточно легко. Но вот с умножением на 6, 7, 8 и 9 возникали определенные трудности. Если бы я знала такой трюк раньше, домашнее задание выполнялось бы минимум в два раза быстрее 😉

©photo

Умножение на 6, 7 и 8

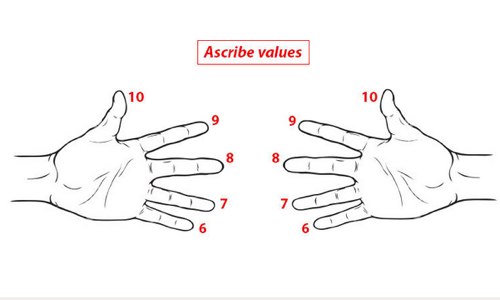таблица умножения на пальцах

Поверните кисти ладонями к себе и присвойте каждому пальцу цифры от 6 и до 10 начиная с мизинца.

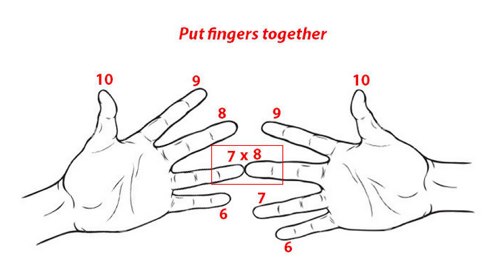
Теперь попробуем умножить, например, 7х8. Для этого соедините палец №7 на левой руке с пальцем №8 на правой.

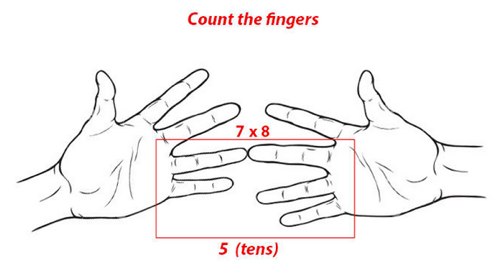таблица умножения на пальцах

А теперь считаем пальцы: количество пальцев под соединенными — это десятки.

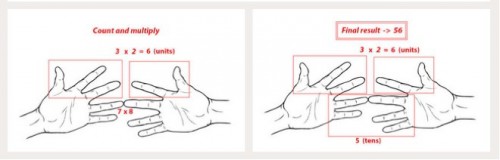таблица умножения на пальцах

(картинка кликабельна)

А пальцы левой руки, оставшиеся сверху, умножаем на пальцы правой — это и будут наши единицы (3х2=6). Итоге равен 56.

Иногда бывает так, что при умножении «единиц» результат получается больше 9. В таких случаях нужно плюсовать оба результата в столбик.

Например, 7х6. В этом случае получается, что «единицы» равны 12 (3х4). В десятки равны 3.

3 (десятки)
+
12 (единицы)
________
42

Умножение на 9

Снова поверните кисти ладонями к себе, но теперь нумерация пальцев будет идти по порядку с лева на право, то есть от 1 до 10.

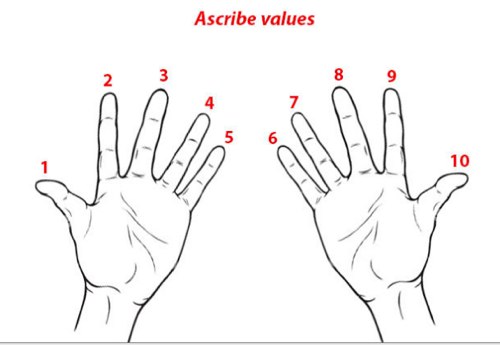
Теперь умножаем, например, 2х9. Все то, что идет до пальца №2 — это десятки (то есть 1 в этом случае). А все то, что остается после пальца №2 — единицы (то есть 8). В итоге получаем 18.