Что такое арифметика 5 класс википедия: История арифметики — Википедия – Арифметика — Вікіпедія — Школа №12 — Научно-образовательный центр школы №12 г. Челябинска

Содержание

Арифметика Википедия

Арифме́тика (др.-греч. ἀριθμητική, arithmētikḗ — от ἀριθμός, arithmṓs «число») — раздел математики, изучающий числа, их отношения и свойства. Предметом арифметики является понятие числа (натуральные, целые, рациональные, вещественные, комплексные числа) и его свойства. В арифметике рассматриваются измерения, вычислительные операции (сложение, вычитание, умножение, деление) и приёмы вычислений. Изучением свойств отдельных целых чисел занимается высшая арифметика, или теория чисел. Теоретическая арифметика уделяет внимание определению и анализу понятия числа, в то время как формальная арифметика оперирует логическими построениями предикатов и аксиом. Арифметика является древнейшей и одной из основных математических наук; она тесно связана с алгеброй, геометрией и теорией чисел^[1]^[2].

Причиной возникновения арифметики стала практическая потребность в счёте и вычислениях, связанных с задачами учёта при централизации сельского хозяйства. Наука развивалась вместе с усложнением задач, требующих решения. Большой вклад в развитие арифметики внесли греческие математики — в частности, философы-пифагорейцы, пытавшиеся с помощью чисел постичь и описать все закономерности мира.

В Средние века арифметику относили, вслед за неоплатониками, к числу так называемых семи свободных искусств. Основными областями практического применения арифметики тогда были торговля, навигация, строительство. В связи с этим особое значение получили приближённые вычисления иррациональных чисел, необходимые, в первую очередь, для геометрических построений. Особенно бурно арифметика развивалась в Индии и странах ислама, откуда новейшие достижения математической мысли проникли в Западную Европу; Россия знакомилась с математическими знаниями «и от греков, и от латин».

С наступлением Нового времени мореходная астрономия, механика, усложнившиеся коммерческие расчёты выдвинули новые требования к технике вычислений и дали толчок к дальнейшему развитию арифметики. В начале XVII века Непер изобрёл логарифмы, а затем Ферма выделил теорию чисел в самостоятельный раздел арифметики. К концу века сформировалось представление об иррациональном числе как о последовательности рациональных приближений, а в течение следующего столетия благодаря трудам Ламберта, Эйлера, Гаусса арифметика включила в себя операции с

Основания математики — Википедия

Основания математики — система общих для всей математики понятий, концепций и методов, с помощью которых строятся различные её разделы^[1].

С античности и приблизительно до конца 17 века источником, описывающим основные понятия и методы математики считался трактат Евклида «Начала» (ок. 300 г. до н. э.). В нём геометрия и теория чисел представлялись как единая аксиоматическая система (на уровне строгости того времени), в которой из исходных предположений (постулатов или аксиом) с помощью выделенного набора логических средств выводились следствия о свойствах первичных понятий (точка, прямая, число и т. д.) и конструируемых из них объектов (геометрические фигуры). Несмотря на отмечавшиеся ещё в античности пробелы в рассуждениях Евклида, его построения в целом считались приемлемыми для описания всего здания тогдашней математики, и до Нового времени последовательной критики не вызывали.

[2]

Положение стало меняться в конце 17 века с изобретением Исааком Ньютоном и Готфридом Вильгельмом Лейбницем дифференциального и интегрального исчислений, логическое обоснование которых долгое время оставалось непроясненным. Оно было получено лишь в середине 19 века стараниями Огюстена Коши, Карла Вейерштрасса, Бернгарда Римана и других математиков на основе предложенного Коши понятия предела, причем проведенный в связи с этим анализ выявил необходимость более детальной, чем у Евклида, систематизации элементарных свойств чисел.

Одновременно с этим появились свидетельства в пользу необходимости пересмотра другой части евклидовых построений, а именно, конструкций, описывающих геометрические объекты. Открытия Николая Лобачевского и Яноша Больяи показали, что, помимо евклидовой геометрии, опирающейся на, как казалось до этого, наиболее интуитивно очевидные аксиоматические предположения, возможны альтернативные геометрии, выводимые из других аксиом, но с такой же достоверностью способные описывать явления природы.

Возникшее у математиков в связи с этим понимание, что фундамент их науки следует перенести в более глубинные её области, оперирующие с объектами, более простыми, чем числа и геометрические фигуры (но такими, чтобы все остальные математические объекты можно было с их помощью построить), привело в последней четверти 19 века Георга Кантора к созданию теории множеств, быстро завоевавшей популярность в качестве нового языка математики. Однако обнаруженные в начале 20 века противоречия в теории Кантора спровоцировали кризис в математике, выявив необходимость пересмотра её оснований.

[2]

Предпринятые вслед за этим исследования в этой области привели к уточнению (формализации) понятий «аксиоматическая система» и «доказательство», перестройке на этой основе математической логики, и к построению формальных аксиоматических теорий множеств, признаваемых ныне фундаментом всей математики.^[3]

Никола Бурбаки определяет математику как «науку об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств, — именно тех, которые в качестве аксиом положены в основание той или иной математической теории».^[4]

Предельная идеализация объектов математики может казаться препятствием к их изучению, однако ещё в древности было замечено, что одним из следствий этой идеализации является, наоборот, возможность установления многочисленных связей между рассматриваемыми объектами вплоть до построения иерархии между ними с выделением элементарных объектов, из которых строятся все остальные

[5]. В античной математике такими элементарными объектами были (понимаемые в значительной мере интуитивно) числа и геометрические формы (точка, линия, поверхность и т. д.)^[6]. В современной математике ими являются множества.^[3]

Этот факт можно считать результатом двух важных наблюдений, сделанных на самом начальном этапе развития теории множеств:

Декартово произведение X×Y{\displaystyle X\times Y} двух множеств X{\displaystyle X} и Y{\displaystyle Y} можно определить как множество упорядоченных пар (x,y){\displaystyle (x,y)}, с x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y}, в котором сами упорядоченные пары (x,y){\displaystyle (x,y)} определяются как множества вида {x,{x,y}}{\displaystyle \{x,\{x,y\}\}} (состоящие из двух элементов, x{\displaystyle x} и {x,y}{\displaystyle \{x,y\}}, причем второй элемент — это множество из двух элементов, x{\displaystyle x} и y{\displaystyle y}).^[7]

^[8]^[9]^[10]^[11]
Функцию или отображение f:X→Y{\displaystyle f:X\to Y} множества X{\displaystyle X} в множество Y{\displaystyle Y} можно также определить как некое множество, а именно, как подмножество в декартовом произведении f⊆X×Y{\displaystyle f\subseteq X\times Y}, удовлетворяющее следующим двум условиям:^[12]^[8]^[13]^[14]

∀x∈X ∃y∈Y:(x,y)∈f{\displaystyle \forall x\in X~\exists y\in Y:(x,y)\in f}	{\displaystyle \quad }	(«для любого x∈X{\displaystyle x\in X} существует y∈Y{\displaystyle y\in Y}, такой что (x,y)∈f{\displaystyle (x,y)\in f}»),
((x,y)∈f∧(x,z)∈f)⟹y=z{\displaystyle \left((x,y)\in f\wedge (x,z)\in f\right)\implies y=z}	{\displaystyle \quad }	(«если (x,y)∈f{\displaystyle (x,y)\in f} и (x,z)∈f{\displaystyle (x,z)\in f}, то y=z{\displaystyle y=z}») .

Первое условие здесь означает, что каждому аргументу x∈X{\displaystyle x\in X} сопоставлено некоторое значение y∈Y{\displaystyle y\in Y} функции f{\displaystyle f}, а второе — что это значение единственно.

Из этих наблюдений следует вывод, серьёзно повлиявший на отношение современников к теории множеств Кантора: все математические объекты, за исключением тех, которые используются в описании самого понятия множества, можно определить как множества с подходящими свойствами.

♦ Как иллюстрация, теория чисел может быть представлена как часть теории множеств, её дефинициальное расширение^[en], если заметить, что изучаемые ею объекты — числа — допускают описания как множества специального вида:^[15]^[16]^[17]

Натуральные (неотрицательные целые) числа N{\displaystyle \mathbb {N} } естественно определяются как конечные ординалы (с отношением порядка и операциями сложения и умножения для ординалов)^[18]^[19]^[20].
Целые числа Z{\displaystyle \mathbb {Z} } затем определяются как элементы фактормножества декартова квадрата N×N{\displaystyle {\mathbb {N} }\times {\mathbb {N} }} множества N{\displaystyle \mathbb {N} } натуральных чисел, по отношению эквивалентности

(n,m)∼(n′,m′) ⟺ n+m′=n′+m,{\displaystyle (n,m)\sim (n’,m’)~\iff ~n+m’=n’+m,}

с отношением порядка^[21]

[(n,m)]≤[(n′,m′)] ⟺ n+m′≤n′+m{\displaystyle [(n,m)]\leq [(n’,m’)]~\iff ~n+m’\leq n’+m}

и алгебраическими операциями

[(n,m)]+[(n′,m′)]=[(n+n′,m+m′)],{\displaystyle [(n,m)]+[(n’,m’)]=[(n+n’,m+m’)],}

[(n,m)]⋅[(n′,m′)]=[(n⋅n′+m⋅m′,n⋅m′+m⋅n′)],{\displaystyle [(n,m)]\cdot [(n’,m’)]=[(n\cdot n’+m\cdot m’,n\cdot m’+m\cdot n’)],}

и при этом вложение N{\displaystyle \mathbb {N} } в Z{\displaystyle \mathbb {Z} } описывается формулой

k∈N↦[(k,0)]∈Z{\displaystyle k\in {\mathbb {N} }\mapsto [(k,0)]\in {\mathbb {Z} }}.

Класс эквивалентности [(n,m)]{\displaystyle [(n,m)]} интерпретируется как целое число n−m{\displaystyle n-m} в обычной записи (с n,m∈N{\displaystyle n,m\in {\mathbb {N} }}).

(p,q)∼(p′,q′) ⟺ q′⋅p=q⋅p′,{\displaystyle (p,q)\sim (p’,q’)~\iff ~q’\cdot p=q\cdot p’,}

с отношением порядка^[23]

[(p,q)]≤[(p′,q′)] ⟺ q′⋅p≤q⋅p′{\displaystyle [(p,q)]\leq [(p’,q’)]~\iff ~q’\cdot p\leq q\cdot p’}

и алгебраическими операциями

[(p,q)]+[(p′,q′)]=[(p⋅q′+p′⋅q,q⋅q′)],{\displaystyle [(p,q)]+[(p’,q’)]=[(p\cdot q’+p’\cdot q,q\cdot q’)],}

[(p,q)]⋅[(p′,q′)]=[(p⋅p′,q⋅q′)],{\displaystyle [(p,q)]\cdot [(p’,q’)]=[(p\cdot p’,q\cdot q’)],}

и при этом вложение Z{\displaystyle \mathbb {Z} } в Q{\displaystyle \mathbb {Q} } описывается формулой

k∈Z↦[(k,1)]∈Q{\displaystyle k\in {\mathbb {Z} }\mapsto [(k,1)]\in {\mathbb {Q} }}.

Класс эквивалентности [(p,q)]{\displaystyle [(p,q)]} интерпретируется как рациональное число p/q{\displaystyle p/q} в обычной записи (с p∈Z{\displaystyle p\in {\mathbb {Z} }}, q∈N∖{0}{\displaystyle q\in {\mathbb {N} }\setminus \{0\}}).

(x,y)+(x′,y′)=(x+x′,y+y′){\displaystyle (x,y)+(x’,y’)=(x+x’,y+y’)},

(x,y)⋅(x′,y′)=(x⋅x′−y⋅y′,x⋅y′+y⋅x′),{\displaystyle (x,y)\cdot (x’,y’)=(x\cdot x’-y\cdot y’,x\cdot y’+y\cdot x’),}

и при этом вложение R{\displaystyle \mathbb {R} } в C{\displaystyle \mathbb {C} } описывается формулой

a∈R↦(a,0)∈C{\displaystyle a\in {\mathbb {R} }\mapsto (a,0)\in {\mathbb {C} }}.

Мнимая единица определяется в этой конструкции как пара i=(0,1){\displaystyle i=(0,1)}, и вместе с предыдущими обозначениями это дает тождество

(x,y)=x+iy,x,y∈R,{\displaystyle (x,y)=x+iy,\quad x,y\in {\mathbb {R} },}

интерпретируемое как обычная алгебраическая запись комплексного числа.

♦ Другая иллюстрация: математический анализ, как теория, описывающая свойства функций на вещественных числах^[24], может считаться дефинициальным расширением теории множеств, потому что обе главные его конструкции — функция (отображение) и вещественное число — как уже было сказано выше, представляют собой множества.

♦ Следующая иллюстрация: в алгебре понятие группы описывается как множество G{\displaystyle G} с заданной на нём операцией m:(x,y)↦m(x,y)=x⋅y{\displaystyle m:(x,y)\mapsto m(x,y)=x\cdot y}, отображающей декартов квадрат G×G{\displaystyle G\times G} в G{\displaystyle G}, и обладающей нужными свойствами (ассоциативность, существование нейтрального элемента 1 и обратного элемента x−1∈G{\displaystyle x^{-1}\in G} для каждого x∈G{\displaystyle x\in G}). Поскольку, как уже объяснялось, отображения представляют собой частный случай множеств, всю конструкцию группы можно интерпретировать как множество G{\displaystyle G} с дополнительной структурой в виде ещё одного множества m{\displaystyle m} с определёнными свойствами.

♦ Основная конструкция топологии, понятие топологического пространства определяется как произвольное множество X{\displaystyle X} с фиксированным множеством U{\displaystyle {\mathcal {U}}} подмножеств в X{\displaystyle X}, содержащим X{\displaystyle X} и ∅{\displaystyle \varnothing }, и замкнутым относительно объединений и конечных пересечений (такое множество U{\displaystyle {\mathcal {U}}} подмножеств в X{\displaystyle X} называется топологией на множестве X{\displaystyle X}, а элементы U{\displaystyle {\mathcal {U}}} — открытыми множествами в X{\displaystyle X}).

♦ Похожим образом, во всей остальной математике (исключая лишь некоторые области математической логики, служащие фундаментом для построения самой теории множеств и/или изучающие формально более общие вопросы) используемые понятия определяются как множества (возможно, некоторого специального вида) с заданными на них дополнительными структурами (которые также определяются как множества нужного вида)^[25]. Таковы, в частности,

решетки, кольца, модули, поля, векторные пространства, более широко, все алгебраические системы в алгебре,
многообразия со всевозможными дополнительными структурами типа метрики, связности, кривизны и т. п. в геометрии,
меры с порождаемыми ими пространствами функций и операторов в анализе,
вероятностные пространства и случайные величины в теории вероятности,
объекты с морфизмами в теории категорий, и т. д.

Фактически, все математические теории описываются ныне как дефинициальные расширения какой-нибудь теории множеств из разработанного для этих целей стандартного списка^[26] (причем в подавляющем большинстве случаев подходит любая теория из этого списка), и именно по этой причине теория множеств считается в наше время языком математики.^[3]

Развитие математики показало, что понятие множества само по себе требует аккуратного определения, чтобы недосказанности в понимании его свойств не приводили к противоречиям. Для решения этой проблемы правила построения теорий, подобных тем, где должны описываться свойства множеств, были строго формализованы, и в нынешних (аксиоматических) теориях, построенных по этим новым правилам, и называемых теориями первого порядка^[27]^[28], элементы двусмысленности исключены, а выбираемые аксиомы проходят первичную проверку на предмет появления очевидных несуразностей.^[29]

Это позволило избавиться от всех появившихся в начале 20 века противоречий в математике (правда, без гарантий, что новые противоречия не появятся в будущем^[30]). С другой стороны, довольно быстро обнаружилось, что предпочтения в выборе аксиом у математиков неодинаковы, и это привело к появлению многочисленных неэквивалентных аксиоматических теорий множеств^[31]. Наибольшей популярностью среди них пользуются ныне

Считается, что у каждой из них есть свои достоинства и недостатки.^[36] Теория ZF исторически появилась первой, и для большинства математических задач её обычно бывает достаточно, поэтому по употребительности она сильно опережает остальные. Однако в современных абстрактных областях математики, в частности, там, где используются методы теории категорий, как, например, в алгебре или в функциональном анализе, бывает желательно рассматривать образования, более общие, чем множества, так называемые классы, которых в ZF нет, и для этих целей обычно выбираются NBG или MK.^[36] Преимуществом NBG в этом списке является её конечная аксиоматизируемость.^[37]^[38] Но по элегантности и спектру возможностей и ZF, и NBG уступают MK.^[36] Недостатком MK (как и NBG) тем не менее является то, что в этой теории нет возможности рассматривать образования, более широкие, чем классы, содержащие произвольные классы как элементы (что также бывает желательно в некоторых математических дисциплинах, как, например, в теории категорий).^[39] Эта проблема предела возможностей решается иногда добавлением к MK (и точно так же этот прием работает в ZF и NBG) аксиомы существования универсума Гротендика с последующим переименованием объектов.^[40]

Вместе современные аксиоматические теории множеств образуют некую систему с общими языком и методами (и различиями только в списках аксиом), целью которой является обеспечение математиков инструментами для построения всех остальных математических объектов, существующих, и тех, которые могут понадобиться в будущем, и эту систему теорий, вместе с той областью математики, внутри которой они строятся, математической логикой, принято называть основаниями математики. Как часть математической логики, сюда входят и альтернативные теории, где вместо множеств в качестве первичных понятий математики предлагаются другие формы, в частности, объекты абстрактных категорий, описываемых не по традиции (как конструкции в ZF, NBG или MK), а напрямую, как независимые теории первого порядка.^[41]

Дошедшие до наших дней труды египетских и вавилонских математиков содержат только алгоритмы вычислений, разъясняемые на практических примерах. Никаких доказательств в них нет; неясно, каким образом открывались и обосновывались результаты, и обосновывались ли вообще. В трудах математиков Древнего Китая встречаются отдельные доказательства алгебраических и геометрических утверждений, однако единой системы логически связанных знаний они не образуют^[42]^[43].

Античный период[править | править код]

Идейные мотивы древнегреческой математики разработала пифагорейская школа, введшая логическое доказательство как необходимый компонент математической теории и разработавшая методологию доказательства, в том числе «доказательство от противного»^[44]. Базовыми объектами пифагорейцев были натуральные числа (дроби у них считались не числами, а пропорциями). Философской основой пифагорейской математики было убеждение в том, что Вселенная была создана по математическому плану, «всё есть число», из чего следовало, что законы природы познаваемы, существует только одна математика, и она содержит систему абсолютных, вечных истин. Успехи применения математики в астрономии (особенно в предсказании затмений), в музыке, оптике и землемерии считались подтверждением этих взглядов. Платон пошёл дальше, объявив, что мате

Сложение — Википедия

В учебниках часто объясняют сложение с помощью яблок и равенства 3 + 2 = 5^[1]

Сложе́ние (прибавле́ние^[2]) — одна из основных бинарных математических операций (арифметических действий) двух аргументов (слагаемых), результатом которой является новое число (сумма), получаемое увеличением значения первого аргумента на значение второго аргумента. То есть каждой паре элементов (a,b){\displaystyle (a,b)} из множества A{\displaystyle A} ставится в соответствие элемент c=a+b{\displaystyle c=a+b}, называемый суммой a{\displaystyle a} и b{\displaystyle b}. Это одна из четырёх элементарных^[en] математических операций арифметики. Приоритет её в обычном порядке операций равен приоритету вычитания, но ниже, чем у возведения в степень, извлечения корня, умножения и деления^[3]. На письме сложение обычно обозначается с помощью знака «плюс»: a+b=c{\displaystyle a+b=c}.
Сложение возможно, только если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип). Так, на картинке справа запись 3+2{\displaystyle 3+2} обозначает три яблока и два яблока вместе, что в сумме дает пять яблок. Но нельзя сложить, например, 3 яблока и 2 груши.

Используя систематические обобщения, сложение можно определить для абстрактных величин, таких как целые числа, рациональные числа, вещественные числа и комплексные числа и для других абстрактных объектов, таких как векторы и матрицы.

У сложения есть несколько важных свойств (например, для A={\displaystyle A=}R{\displaystyle \mathbb {R} }) (см. Сумма):

Коммутативность: a+b=b+a,∀a,b∈ A{\displaystyle a+b=b+a,\quad \forall a,b\in \ A}^{[см. «Коммутативность»]}

Ассоциативность: (a+b)+c=a+(b+c),∀a,b,c∈ A{\displaystyle (a+b)+c=a+(b+c),\quad \forall a,b,c\in \ A}^{[см. «Ассоциативность»]}

Дистрибутивность: x⋅(a+b)=(x⋅a)+(x⋅b),∀a,b∈ A.{\displaystyle x\cdot (a+b)=(x\cdot a)+(x\cdot b),\quad \forall a,b\in \ A.}

Прибавление 0{\displaystyle 0} (нулевого элемента) даёт число, равное исходному: x+0=0+x=x,∀x∈A,∃0∈A.{\displaystyle x+0=0+x=x,\quad \forall x\in A,\quad \exists 0\in A.}

Сложение очень маленьких чисел понятно даже детям. В начальной школе учат считать в десятичной системе счисления и постепенно переходят к более сложным задачам.

Известны различные устройства для сложения: от древних абаков до современных компьютеров.

$x+0=0+x=x,\quad \forall x\in A,\quad \exists 0\in A.$

Сложение записывается с использованием символа плюса «+» между слагаемыми; такая форма записи называется инфиксной нотацией. Результат записывается с использованием знака равенства. Например,

a+b=c{\displaystyle a+b=c} («а плюс бэ равно цэ»)

1+1=2{\displaystyle 1+1=2} («один плюс один равно двум»)

2+2=4{\displaystyle 2+2=4} («два плюс два равно четырём»)

5+4+2=11{\displaystyle 5+4+2=11} (см. «ассоциативность» ниже)

3+3+3+3=12{\displaystyle 3+3+3+3=12} (см. «умножение» ниже)

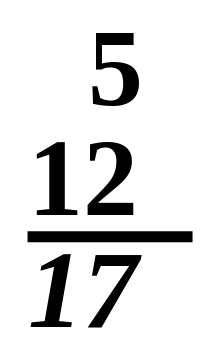Сложение в столбик:
5 + 12 = 17

В ряде ситуаций подразумевается сложение, но при этом символы сложения не используются:

В записи чисел в позиционных системах счисления: запись числа an−1an−2…a1a0,{\displaystyle a_{n-1}\;a_{n-2}\ldots \;a_{1}\;a_{0},} подразумевает суммирование ряда an−1⋅Pn−1+an−2⋅Pn−2+…+a1⋅P1+a0⋅P0{\displaystyle a_{n-1}\cdot P^{n-1}+a_{n-2}\cdot P^{n-2}+\ldots +a_{1}\cdot P^{1}+a_{0}\cdot P^{0}}^[4].
Если имеется столбец чисел, последнее (нижнее) число в котором подчёркнуто, то обычно подразумевается, что все числа в этом столбце складываются, а полученная сумма записывается ниже подчеркнутого числа.
Если имеется запись, когда перед дробью стоит целое число, то эта запись означает сумму двух слагаемых — целого числа и дроби, которую называют смешанным числом^[5]. Например,
3½ = 3 + ½ = 3.5.
Такая запись может вызвать путаницу, поскольку в большинстве других случаев подобная запись означает умножение, а не сложение^[6].

Сумма ряда связанных чисел может быть записана с использованием символа Σ, который позволяет компактно записать итерацию. Например,

∑k=15k2=12+22+32+42+52=55.{\displaystyle \sum _{k=1}^{5}k^{2}=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}=55.}

Слагаемые — это числа или объекты, складываемые друг с другом^[7].

Символ плюса «+» (Юникод:U+002B; ASCII: +) — упрощение латинского слова «et», означающего «и»^[8]. Впервые этот символ встречается в книгах, начиная с 1489 г.^[9]

Сложение используется для моделирования бесчисленного множества физических процессов. Даже для простого сложения натуральных чисел существует много различных интерпретаций и ещё больше способов визуального представления.

Комбинирование наборов[править | править код]

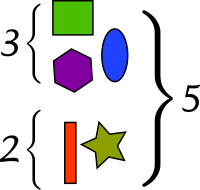
Возможно, самая фундаментальная интерпретация сложения — комбинирование наборов:

Если два или более не пересекающихся наборов объектов объединены в один набор, то число объектов в полученном наборе равно сумме числа объектов в исходных наборах.

Эту интерпретацию легко визуализировать, при этом опасность двусмысленности будет минимальной. Однако непонятно, как с помощью этой интерпретации сложения объяснить сложение дробных или отрицательных чисел^[10].

Одним из возможных решений будет обращение к набору объектов, которые могут быть легко разделены, например, пироги или стержни с сегментами^[11]. Вместо комбинирования наборов сегментов стержни могут быть присоединены друг к другу концами, что иллюстрирует другую концепцию сложения: складываются не стержни, складываются их длины.

Расширение длины[править | править код]

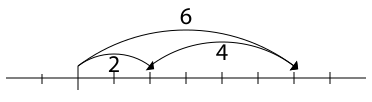
Визуализация суммы 2 + 4 = 6 на числовой прямой. Сдвиг на 2 и затем сдвиг на 4 — это то же самое, что и сдвиг на 6.

Еще один вариант визуализации суммы 2 + 4 = 6 на числовой прямой. Сдвиг на 4 — это то же самое, что и четыре сдвига по 1.

Вторая интерпретация сложения заключается в расширении начальной длины на величину добавляемой длины:

Когда начальная длина расширяется добавляемой длиной, то полученная длина равна сумме начальной длины и длины, которую к ней добавили^[12].

Сумму a + b можно интерпретировать как бинарную операцию объединения a и b в алгебраическом смысле, также её можно интерпретировать как добавление b единиц к числу a. В последней интерпретации части суммы a + b играют асимметричные роли, и операция a + b рассматривается как применение к числу a унарной операции +b^[13]. Унарный подход позволяет перейти к вычитанию, ведь каждая унарная операция сложения имеет обратную унарную операцию вычитания и наоборот.

Операция сложения на числовых множествах N,Z,Q,R,C{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} } имеет следующие основные свойства:

Коммутативность[править | править код]

$\mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C}$

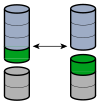
Визуализация 4 + 2 = 2 + 4 при помощи блоков

Сложение коммутативно — от перемены мест слагаемых сумма не меняется (это свойство также известно как переместительный закон сложения): a+b=b+a,∀a,b∈ A.{\displaystyle a+b=b+a,\quad \forall a,b\in \ A.} Есть и другие законы коммутативности: например, существует коммутативный закон умножения. Тем не менее многие бинарные операции, например, вычитание и деление, не коммутативны.

Ассоциативность[править | править код]

$a+b=b+a,\quad \forall a,b\in \ A.$ Визуализация 2+(1+3) = (2+1)+3 при помощи стержней с сегментами

Сложение ассоциативно — при последовательном выполнении сложения трёх или более чисел последовательность выполнения операций не имеет значения (сочетательный закон сложения): (a+b)+c=a+(b+c),∀a,b,c∈ A.{\displaystyle (a+b)+c=a+(b+c),\quad \forall a,b,c\in \ A.}

Дистрибутивность[править | править код]

Сложение дистрибутивно, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве (распределительный закон)^[14] : x⋅(a+b)=(x⋅a)+(x⋅b),∀a,b∈ A.{\displaystyle x\cdot (a+b)=(x\cdot a)+(x\cdot b),\quad \forall a,b\in \ A.}

Нейтральный элемент[править | править код]

$x\cdot (a+b)=(x\cdot a)+(x\cdot b),\quad \forall a,b\in \ A.$

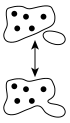Визуализация 5 + 0 = 5 при помощи сумок с точками

Относительно сложения в множестве A{\displaystyle A} существует единственный нейтральный элемент, сложение числа с 0{\displaystyle 0} (нулевым или нейтральным элементом) даёт число, равное исходному: x+0=0+x=x,∀x∈A,∃0∈A.{\displaystyle x+0=0+x=x,\quad \forall x\in A,\quad \exists 0\in A.}

Этот закон был впервые описан в Исправленном трактате Брахмы^[en], который был написан Брахмагуптой в 628 г. Он написал этот закон в виде трёх отдельных законов: для отрицательного, положительного и нулевого числа a, и для описания этих законов он использовал слова, а не алгебраические символы. Позже индийские математики уточнили понятия; около 840 г., Махавира^[en] написал, что «ноль становится таким же, как то, что добавляется к нему», что соответствовало записи 0 + a = a. В XII веке Бхаскара II написал: «Если добавить ничего или вычесть ничего, то количество, положительное или отрицательное, остаётся таким же, как и было», что соответствует записи a + 0 = a^[15].

Обратный элемент[править | править код]

Сложение с противоположным элементом даёт 0{\displaystyle 0}: a+(−a)=0,∀a∈A,∃−a∈A.{\displaystyle a+(-a)=0,\quad \forall a\in A,\quad \exists -a\in A.}^[16]

Кроме того, сложение не выводит результат за пределы данного множества чисел, следовательно, N,Z,Q,R,C{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} } замкнуты относительно операции сложения. Эти множества с операциями +{\displaystyle +} и ⋅{\displaystyle \cdot } образуют кольца (коммутативные кольца с единицей)^[17]. На языке общей алгебры вышеперечисленные свойства сложения говорят о том, что Z,Q,R,C{\displaystyle \mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} } — абелевы группы относительно операции сложения.

Операцию сложения можно представить как некий «черный ящик» с двумя слагаемыми на входе и одним выходом — суммой:^[18]^[19]

При практическом решении задачи сложения двух чисел необходимо свести её к последовательности более простых операций: «простое сложение»^{[источник не указан 1241 день]}, перенос, сравнение и др. Для этого разработаны различные методы сложения, например для чисел, дробей, векторов и др. На числовых множествах используется алгоритм поразрядного сложения^[20]. При этом следует рассматривать сложение как процедуру (в отличие от операции).

Примерный алгоритм процедуры поразрядного сложения двух чисел^[21]

Как видим, процедура достаточно сложная, состоит из относительно большого числа шагов и при сложении больших чисел может занять продолжительное время.

«Простое сложение» — в данном контексте обозначает операцию сложения одноразрядных чисел, которая может быть легко сведена к инкрементированию.^{[источник не указан 1241 день]} Является гипероператором инкрементирования:

Пример пошагового сложения чисел 2 и 4 на числовой прямой.

a+b=hyper1⁡(a,b)=hyper⁡(a,1,b)=a(1)b.{\displaystyle a+b=\operatorname {hyper1} (a,b)=\operatorname {hyper} (a,1,b)=a^{(1)}b.}

a(1)b=a+b=1+1+⋯+1⏟a+1+1+⋯+1⏟b.{\displaystyle a{^{(1)}}b=a+b=\underbrace {1+1+\dots +1} _{a}+\underbrace {1+1+\dots +1} _{b}.}

где 1+1+⋯+1{\displaystyle 1+1+\dots +1} — последовательность операций инкрементирования, выполненная a{\displaystyle a} и b{\displaystyle b} раз.

Врождённая способность[править | править код]

Исследования развития математических способностей, которые начались в 1980-х годах, рассматривали феномен привыкания: младенцы смотрят дольше на ситуации, которые являются для них неожиданными^[22]. В эксперименте Карен Винн^[en] 1992 года использовались куклы Микки Мауса, с которыми проводились различные манипуляции за ширмой. Этот эксперимент показал, что пятимесячные младенцы ожидают, что 1 + 1 — это 2, и удивляются тому, когда оказывается, что 1 + 1 — это 1 или 3. Позже этот результат был подтверждён в других лабораториях с использованием разных методов^[23]. В другом эксперименте в 1992 году с малышами постарше, в возрасте от 18 до 35 месяцев, использовалось развитие моторных функций детей, позволявшее им доставать шарики для пинг-понга из коробки; младшие ребята хорошо справлялись с небольшим числом шариков, более старшие научились считать сумму до 5^[24].

Даже некоторые животные проявляют способность складывать, в особенности приматы. Эксперимент 1995 года был аналогичен эксперименту Винн 1992 года, но вместо кукол использовались баклажаны. Выяснилось, что макаки-резусы и эдиповы тамарины показывают схожие человеческим младенцам способности. Более того, один шимпанзе, после того, как его научили различать и понимать смысл арабских цифр от 0 до 4, смог считать сумму двух чисел без какой-либо подготовки^[25]. Позже было выяснено, что азиатские слоны способны овладеть базовыми арифметическими операциями^[26].

Овладение сложением детьми[править | править код]

Как правило, сначала дети учатся подсчёту^[en]. Когда даётся задача, в которой требуется объединить два предмета и три предмета, маленькие дети обращаются к помощи конкретных предметов, например, счёт на пальцах или помощь рисунка. По мере приобретения опыта, они учат или открывают для себя стратегию «подсчета»: когда требуется найти, сколько будет два плюс три, дети перечисляют два числа, идущие после числа три, проговаривая: «три, четыре, пять» (обычно загибая пальцы), и, в итоге, получая пять. Эта стратегия кажется почти универсальной; дети могут легко перенять её у сверстников или учителей^[27]. Многие дети сами доходят до этого. Накопив какой-то опыт, дети учатся складывать быстрее, используя коммутативность сложения, начиная перечислять числа от самого большого числа в сумме, как в описанном выше случае, начиная с трёх и перечисляя: «четыре, пять». В конце концов, дети начинают использовать какие-либо факты о сложении («примеры сложения наизусть^[en]»), получая их либо опытным путём, либо запоминая их. Когда одни факты осядут в памяти, дети начинают выводить неизвестные факты из известных. Например, ребёнок, складывающий шесть и семь, может знать, что 6 + 6 = 12, и что поэтому 6 + 7 на один больше, то есть 13^[28]. К такому способу вывода приходят довольно быстро и большинство учеников начальной школы полагаются на смесь всего того, что они запомнили и того, что они могут вывести, что в итоге позволяет им бегло складывать^[29].

В разных странах к изучению целых чисел и арифметики приступают в разных возрастах, в основном сложению учат в учреждениях дошкольного образования^[30]. При этом по всему миру к концу первого года начальной школы школьники обучаются сложению^[31].

Таблица сложения[править | править код]

Детям часто показывают таблицу сложения пар чисел от 1 до 10 для лучшего запоминания^{[обтекаемое выражение]}. Зная эту таблицу, можно выполнить любое сложение.

таблица для сложения в десятичной системе счисления

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

Десятичная система[править | править код]

Для успешного сложения в десятичной системе нужно помнить или уметь быстро выводить 100 «фактов (примеров) сложения» для одноразрядных чисел. Кто-то может запомнить все эти факты, заучивая их, но стратегии изучения сложения путём использования шаблонов более информативны и для большинства людей более эффективны:^[32]

Коммутативное свойство: использование шаблона a+b=b+a{\displaystyle a+b=b+a} снижает количество «фактов о сложении», которых нужно запомнить, со 100 до 55.
На один или на два больше: прибавление 1 или 2 — это базовая задача, и решить её можно перечислением (подсчетом) или, в конце концов, полагаясь на интуицию^[32].
Ноль: поскольку ноль является нейтральным элементом для операции сложения (аддитивной единицей), постольку прибавить ноль просто. Тем не менее, во время изучения арифметики некоторым ученикам сложение представляется как процесс, во время которого слагаемые всегда увеличиваются; акцент на словесной формулировке^[en] задачи может помочь понять «исключительность» нуля^[32].
Удваивание: складывание числа с самим собой связано с задачей удвоенного (повторного) подсчёта и умножением. Факты об удваивании являются основой для многих связанных с ними фактов, и ученикам легко их относительно легко понять^[32].
Почти-удваивание (Суммы, близкие к операции удваивания): сумма 6 + 7 = 13 может быть быстро выведена из факта об удваивании 6 + 6 = 12 и прибавления единицы, или из факта 7 + 7 = 14 и вычитания единицы^[32].
Пять и десять: суммы вида 5 + x и 10 + x обычно запоминаются рано и могут быть использованы для выведения других фактов. Например, результат суммы 6 + 7 = 13 может быть выведен с использованием факта 5 + 7 = 12 добавлением к последнему единицы^[32].
Получение десятки (достраивание до десяти): существует такая стратегия, в которой 10 используется в качестве промежуточного результата при наличии слагаемых 8 или 9; например, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14^[32].

По мере взросления ученики запоминают всё больше фактов, и учатся быстро выводить из них другие факты. Многие ученики не запоминают все факты, но могут быстро вывести требуемый^[29].

Перенос[править | править код]

В стандартном алгоритме сложения многоразрядных чисел^{[обтекаемое выражение]} цифры, из которых состоят записи складываемых чисел, располагаются одна под другой. Выполняют сложение цифр отдельно в каждом столбце, начиная с правого. Если сумма цифр в столбце превышает 10, лишняя цифра «переносится» в следующий столбец (левее). Например, в сумме 27 + 59

  ¹
  27
+ 59
————
  86

7 + 9 = 16 и цифра 1 переносится в следующий столбец. В альтернативном способе начинают сложение с наиболее значимой цифры слева; в этой стратегии перенос выполняется несколько грубее, но быстрее получается приблизительная сумма. Существует много других методов переноса.

Сложение десятичных дробей[править | править код]

Способ сложения десятичных дробей является простой модификацией сложения многоразрядных чисел, описанного выше^[33]. При сложении столбиком дроби располагают таким образом, чтобы запятые^[стиль] находились точно друг под другом. При необходимости можно добавлять нули справа и слева к более короткой дроби (см. замыкающий ноль^[en] и ведущие нули), чтобы сделать её равной по длине более длинной дроби. Итак, сложение производится таким же образом, как и в описанном выше способе сложения многоразрядных чисел, только запятая располагается в ответе точно там же, где она располагалась у слагаемых.

Например, сумму 45,1 + 4,34 можно вычислить следующим образом:

   4 5 , 1 0
+  0 4 , 3 4
————————————
   4 9 , 4 4

Экспоненциальная запись[править | править код]

В экспоненциальной записи числа записываются в виде a=±x⋅P±n{\displaystyle a=\pm x\cdot P^{\pm n}}, где x{\displaystyle x} — мантисса, Pn{\displaystyle P^{n}} — характеристика числа, P{\displaystyle P} — основание системы счисления. Для сложения двух чисел, которые записаны в экспоненциальной форме, требуется, чтобы у них были одинаковые характеристики: a⋅Pn+b⋅Pn=(a+b)⋅Pn,{\displaystyle a\cdot P^{n}+b\cdot P^{n}=(a+b)\cdot P^{n},} согласно свойству дистрибутивности.

Например:

2.3⋅10−5+5.67⋅10−6=2.34⋅10−5+0.567⋅10−5=(2.34+0.567)⋅10−5=2.907⋅10−5{\displaystyle 2.3\cdot 10^{-5}+5.67\cdot 10^{-6}=2.34\cdot 10^{-5}+0.567\cdot 10^{-5}=(2.34+0.567)\cdot 10^{-5}=2.907\cdot 10^{-5}}

Особый случай — сложение чисел, различающихся на несколько порядков, с последовательным округлением. Если a≫b{\displaystyle a\gg b}, то и погрешности этих чисел будут несопоставимы (

Порядковое число — Википедия

Изображение порядковых чисел от 0 до ωω{\displaystyle \omega ^{\omega }}. Каждый оборот спирали соответствует одной степени ω{\displaystyle \omega }

В теории множеств порядковым числом, или ординалом (лат. ordinalis — порядковый) называется порядковый тип вполне упорядоченного множества. Как правило, порядковые числа отождествляются с наследственно транзитивными множествами. Ординалы представляют собой одно из расширений натуральных чисел, отличающееся как от целых, так и от кардинальных чисел. Как и другие разновидности чисел, их можно складывать, перемножать и возводить в степень. Бесконечные порядковые числа называют трансфинитными (лат. trans — за, через + finitio — край, предел). Ординалы играют ключевую роль в доказательстве многих теорем теории множеств — в частности, благодаря связанному с ними принципу трансфинитной индукции.

Порядковые числа были введены Георгом Кантором в 1883 году как способ описания бесконечных последовательностей, а также классификации множеств, обладающих определённой упорядоченной структурой.^[1] Он случайно открыл порядковые числа, работая над задачей, связанной с тригонометрическими рядами.

Множества S{\displaystyle S} и S′{\displaystyle S’} обладают одинаковой мощностью, если между ними можно установить биективное соответствие (то есть указать такую функцию f{\displaystyle f}, которая одновременно является инъективной и сюръективной: каждому x{\displaystyle x} из S{\displaystyle S} соответствует единственное y=f(x){\displaystyle y=f(x)} из S′{\displaystyle S’}, а каждое y{\displaystyle y} из S′{\displaystyle S’} является образом единственного x{\displaystyle x} из S{\displaystyle S}).

Предположим, что на множествах S{\displaystyle S} и S′{\displaystyle S’} заданы частичные порядки <{\displaystyle <} и <′{\displaystyle <‘} соответственно. Тогда частично упорядоченные множества (S,<){\displaystyle (S,<)} и (S′,<′){\displaystyle (S’,<‘)} называются изоморфными с сохранением порядка, если существует биективное отображение f{\displaystyle f}, при которой заданный порядок сохраняется. Иначе говоря, f(a)<′f(b){\displaystyle f(a)<‘f(b)} тогда и только тогда, когда a<b{\displaystyle a<b}. Любое вполне упорядоченное множество (S,<){\displaystyle (S,<)} изоморфно с сохранением порядка по отношению к естественно упорядоченному множеству порядковых чисел, меньших некоторого определённого ординала (равного порядковому типу (S,<){\displaystyle (S,<)}).

Конечные порядковые (и кардинальные) числа представляют собой числа натурального ряда: 0, 1, 2, …, поскольку два любых полных упорядочения конечного множества изоморфны с сохранением порядка. Наименьшее бесконечно большое порядковое число ω{\displaystyle \omega } отождествляется с кардинальным числом ℵ0{\displaystyle \aleph _{0}}. Однако в случае трансфинитных чисел, больших ω{\displaystyle \omega }, ординалы — по сравнению с кардинальными числами — позволяют выразить более тонкую классификацию множеств, основанную на информации об их упорядоченности. В то время как все счетные множества описываются одним кардинальным числом, равным ℵ0{\displaystyle \aleph _{0}}, число счетных ординалов бесконечно велико и притом несчетно:

ω,ω+1,ω+2,…,ω⋅2,ω⋅2+1,…,ω2,…,ω3,…,ωω,…,ωωω,…,ε0,…{\displaystyle \omega ,\omega +1,\omega +2,\dots ,\omega \cdot 2,\omega \cdot 2+1,\dots ,\omega ^{2},\dots ,\omega ^{3},\dots ,\omega ^{\omega },\dots ,\omega ^{\omega ^{\omega }},\dots ,\varepsilon _{0},…}

В данном случае сложение и умножение не обладают свойством коммутативности: так, 1+ω{\displaystyle 1+\omega } совпадает с ω{\displaystyle \omega }, но отличается от ω+1{\displaystyle \omega +1}; аналогично 2⋅ω=ω{\displaystyle 2\cdot \omega =\omega }, но не равно ω⋅2{\displaystyle \omega \cdot 2}. Множество всех счетных ординалов образует первое несчетное порядковое число ω1{\displaystyle \omega _{1}}, соответствующее кардинальному числу ℵ1{\displaystyle \aleph _{1}} (следующее число после ℵ0{\displaystyle \aleph _{0}}). Вполне упорядоченные кардинальные числа отождествляются с их начальными ординалами, то есть минимальными ординалами соответствующей мощности. Мощность порядкового числа задает между классами порядковых и кардинальных чисел соответствие по типу «многие к одному».

Обычно произвольный ординал α{\displaystyle \alpha } определяется как порядковый тип множества ординалов, строго меньших α{\displaystyle \alpha }. Данное свойство позволяет представить любое порядковое число в виде множества ординалов, строго меньших его самого. Все порядковые числа можно разбить на три категории: нуль, следующее порядковое число и предельное порядковое число (последние различаются своей конфинальностью). Для заданного класса порядковых чисел можно указать его α{\displaystyle \alpha }-й элемент — иначе говоря, элементы класса можно проиндексировать (сосчитать). Такой класс будет замкнутым и неограниченным при условии, что функция индексирования непрерывна и никогда не останавливается. Нормальная форма Кантора позволяет единственным образом представить любое порядковое число в виде конечной суммы порядковых степеней ω{\displaystyle \omega }. Тем не менее, такая форма не может использоваться в качестве основы для универсальной системы обозначения порядковых чисел из-за наличия в ней автореферентных представлений: например, ε0=ωε0{\displaystyle \varepsilon _{0}=\omega ^{\varepsilon _{0}}}. Можно определять все более крупные порядковые числа, однако по мере роста их описание усложняется. Любое порядковое число можно представить в виде топологического пространства, приписав ему порядковую топологию. Такая топология будет дискретной, тогда и только тогда, когда соответствующий ординал не превышает счётного кардинального числа, то есть меньше или равен ω{\displaystyle \omega }. Подмножество ω+1{\displaystyle \omega +1} будет открытым в порядковой топологии тогда и только тогда, когда оно является кофинитным или не содержит ω{\displaystyle \omega } в качестве элемента.

Порядковые числа как расширение множества натуральных чисел[править | править код]

Натуральные числа (к которым в данном случае относится и 0) имеют два основных применения: описание размера некоторого множества и описание позиции элемента в заданной последовательности. В случае конечных множеств эти понятия совпадают; с точностью до изоморфизма существует единственный способ расположить элементы конечного множества в виде последовательности. В случае же бесконечных множеств необходимо отличать понятие размера и связанных с ним кардинальных чисел от понятия позиции, обобщением которого служат описанные в данной статье порядковые числа. Это объясняется тем, что бесконечное множество, обладая однозначно определённым размером (мощностью), может быть вполне упорядочено более чем одним неизоморфным способом.

В то время как понятие кардинального числа, связанного с множеством, не требует задания на нём какой-либо структуры, ординалы тесно связаны с особой разновидностью множеств, которые называются вполне упорядоченными (в сущности эти понятия настолько близки, что некоторые математики не делают между ними никаких различий). Данный термин обозначает линейно упорядоченное множество (то есть множество с некоторым единообразным способом выбора наименьшего и наибольшего значения для произвольной пары элементов), в котором нет бесконечно убывающих последовательностей (хотя могут существовать бесконечно возрастающие), или — в эквивалентной формулировке — множество, в котором любое непустое подмножество содержит наименьший элемент. Порядковые числа можно использовать как для обозначения элементов любого заданного вполне упорядоченного множества (наименьший элемент получает метку 0, следующий за ним — метку 1, следующий — 2, «и так далее»), так и для измерения «размера» всего множества путём указания наименьшего ординала, который не является меткой какого-либо элемента множества. Такой «размер» называется порядковым типом множества.

Любое порядковое число определяется множеством предшествующих ординалов: фактически наиболее распространенное определение порядкового числа отождествляет его со множеством предшествующих ординалов. Так, ординал 42 представляет собой порядковый тип множества предшествующих ординалов, то есть ординалов от 0 (наименьший ординал) до 41 (непосредственный предшественник 42), и обычно отождествляется со множеством {0, 1, 2, …, 41}. Верно и обратное: любое замкнутое вниз множество ординалов S{\displaystyle S} — то есть такое, что для любого ординала α∈S{\displaystyle \alpha \in S} и произвольного ординала β<α{\displaystyle \beta <\alpha } ординал β{\displaystyle \beta } также является элементом S{\displaystyle S} — само является ординалом (либо его можно отождествить с таковым).

До этого момента мы упоминали только конечные ординалы, совпадающие с натуральными числами. Помимо них существуют также и бесконечные ординалы: наименьшим среди них является порядковый тип натуральных чисел (конечных ординалов) ω{\displaystyle \omega }, который даже можно отождествить с самим множеством натуральных чисел (действительно: множество натуральных чисел замкнуто вниз и, как любое множество ординалов, является вполне упорядоченным, — следовательно, его можно отождествить с соответствующим порядковым числом, что в точности соответствует определению ω{\displaystyle \omega }).

Вероятно, более интуитивное представление о порядковых числах можно получить, рассмотрев несколько их первых представителей: как уже упоминалось выше, множество ординалов начинается с натуральных чисел 0, 1, 2, 3, 4, 5, … После всех натуральных чисел располагается первый бесконечный ординал ω{\displaystyle \omega }, за которым следуют ω+1{\displaystyle \omega +1}, ω+2{\displaystyle \omega +2}, ω+3{\displaystyle \omega +3}, и так далее. (Точный смысл сложения будет определён далее, поэтому считайте эту запись простым обозначением) После всех таких чисел располагаются ω⋅2{\displaystyle \omega \cdot 2} (то есть ω+ω{\displaystyle \omega +\omega }), ω⋅2+1{\displaystyle \omega \cdot 2+1}, ω⋅2+2{\displaystyle \omega \cdot 2+2}, и так далее, затем ω⋅3{\displaystyle \omega \cdot 3}, а после него — ω⋅4{\displaystyle \omega \cdot 4}. Далее, множество ординалов, которые можно записать в виде ω⋅m+n{\displaystyle \omega \cdot m+n}, где m{\displaystyle m} и n{\displaystyle n} — натуральные числа, также должно обладать соответствующим порядковым числом: таким числом будет ω2{\displaystyle \omega ^{2}}. За ним последуют ω3{\displaystyle \omega ^{3}}, ω4{\displaystyle \omega ^{4}},…, ωω{\displaystyle \omega ^{\omega }}, затем ωω2{\displaystyle \omega ^{\omega ^{2}}} и — намного позже — ε0{\displaystyle \varepsilon _{0}} («эпсилон-нуль») (перечисленные примеры дают представление о сравнительно небольших счетных ординалах). Этот процесс можно продолжать неограниченно (выражение «неограниченности» — это и есть сильная сторона порядковых чисел: собственно говоря, когда мы, перечисляя порядковые числа, употребляем выражение «и так далее», мы тем самым определяем порядковое число большего размера). Наименьший несчетный ординал представляет собой множество всех счетных ординалов и обозначается ω1{\displaystyle \omega _{1}}.

Для обозначения порядковых чисел обычно используются строчные греческие буквы α,β,…{\displaystyle \alpha ,\beta ,\dots } Данная статья придерживается таких обозначений.

Вполне упорядоченные множества[править | править код]

Каждое непустое подмножество вполне упорядоченного множества содержит наименьший элемент. При соблюдении аксиомы зависимого выбора это утверждение эквивалентно тому, что множество линейно упорядочено и не содержит бесконечно убывающих последовательностей — последняя формулировка, вероятно, проще поддается визуализации. На практике важность понятия вполне упорядоченности объясняется возможностью применения трансфинитной индукции, основная идея которой сводится к тому, что любое свойство, переходящее от предшественников элемента к нему самому, должно выполняться для всех элементов (входящих в заданное вполне упорядоченное множество). Если вычислительные состояния (компьютерной программы или игры) можно вполне упорядочить так, что каждый последующий шаг будет «меньше» предыдущего, то процесс вычислений гарантированно завершится.

Далее, мы не хотим различать два вполне упорядоченных множества, если они отличаются только «маркировкой своих элементов», или, говоря более формальным языком, если элементы первого множества можно так соотнести с элементам второго, что в произвольно взятой паре элементов одного множества первый меньше второго тогда и только тогда, когда то же соотношение имеет место между их соответствующими партнерам из второго множества. Такое взаимно однозначное соответствие называется изоморфизмом, сохраняющим порядок, а два вполне упорядоченных множества называются изоморфными с сохранением порядка, или же подобными (такое подобие очевидно является отношением эквивалентности). Если два вполне упорядоченных множества изоморфны с сохранением порядка, то соответствующий изоморфизм является единственным: это обстоятельство позволяет воспринимать упомянутые множества как практически идентичные и служит основанием для поисков «каноничного» представления типов изоморфизма (классов). Порядковые числа не только играют роль такого представления, но ещё и предоставляют нам каноническую маркировку элементов любого вполне упорядоченного множества.

Иными словами, мы хотим ввести понятие ординала как класса изоморфизмов вполне упорядоченных множеств, то есть класса эквивалентности, основанного на отношении «изоморфности с сохранением порядка». При таком подходе, однако, существует одна техническая сложность: определённый таким образом класс эквивалентности оказывается слишком большим, чтобы подходить под определением множества с точки зрения стандартной формализации теории множеств по Цермело-Френкелю. Тем не менее, эта сложность не создает серьезных проблем. Ординалом мы будем называть порядковый тип произвольного множества в таком классе.

Определение порядковых чисел как классов эквивалентности[править | править код]

В первоначальном определении порядкового числа, которое можно встретить, к примеру, в Principia Mathematica, под порядковым типом некоторого вполне-упорядочения понимается множество всех вполне-упорядочений, подобных ему (изоморфных с сохранением порядка): иначе говоря, порядковое число действительно представляет собой класс эквивалентности вполне упорядоченных множеств. В ZFC-теории и связанных с ней аксиоматических системах теории множеств такое определение неприемлемо, поскольку соответствующие классы эквивалентности слишком велики, чтобы их можно было считать множествами. Тем не менее, данное определение можно использовать в теории типов и аксиоматической теории множеств Куайна (Новые основания), а также других подобных системах (в которых оно позволяет сформулировать альтернативный и довольно неожиданный способ разрешения парадокса Бурали-Форти о наибольшем порядковом числе).

Определение порядковых чисел по фон Нейману[править | править код]

Вместо того, чтобы определять ординал как класс эквивалентности вполне упорядоченных множеств, мы отождествим его с конкретным множеством, которое служит каноничным представлением данного класса. Таким образом, ординал будет представлять собой некоторое вполне упорядоченное множество, а любое вполне упорядоченное множество будет подобно ровно одному порядковому числу.

Стандартное определение, предложенное фон Нейманом, звучит следующим образом: любой ординал есть вполне упорядоченное множество, состоящее из всех ординалов, меньших его. В символической записи: λ=[0,λ){\displaystyle \lambda =[0,\lambda )}.^[2]^[3] Выражаясь более формальным языком,

Множество S{\displaystyle S} является ординалом тогда и только тогда, когда оно строго вполне упорядочено отношением ∈{\displaystyle \in } и каждый элемент S одновременно является его подмножеством.

Заметим, что в соответствии с этим определением натуральные числа являются ординалами. Так, 2 принадлежит 4 = {0, 1, 2, 3} и в то же время равно {0, 1}, то есть является подмножеством {0, 1, 2, 3}.

С помощью трансфинитной индукции можно показать, что любое вполне упорядоченное множество подобно ровно одному ординалу — иначе говоря, между ними можно установить биективное соответствие, сохраняющее порядок.

Более того, элементы любого ординала сами являются ординалами. Если S{\displaystyle S} и T{\displaystyle T} — произвольные ординалы, то S{\displaystyle S} принадлежит T{\displaystyle T} тогда и только тогда, когда S{\displaystyle S} является собственным подмножеством T{\displaystyle T}. Далее, для любых ординалов S{\displaystyle S} и T{\displaystyle T} выполняется одно из соотношений: либо S∈T{\displaystyle S\in T}, либо T∈S{\displaystyle T\in S}, либо S=T{\displaystyle S=T}. Таким образом, любое множество ординалов обладает линейной упорядоченностью и, кроме того, является вполне упорядоченным. Данный результат служит обобщением вполне упорядоченности натуральных чисел.

Отсюда следует, что элементы произвольного ординала S{\displaystyle S} в точности совпадают с ординалами, строго меньшими S{\displaystyle S}. Каждое множество ординалов, к примеру, обладает супремумом, который представляет собой ординал, равный объединению всех порядковых чисел, содержащихся в данном множестве. В силу аксиомы объединения такой ординал существует всегда, независимо от размера исходного множества.

Класс всех порядковых чисел не является множеством. В противном случае можно было бы доказать, что такое множество само является порядковым числом и, следовательно, своим собственным элементом, что противоречит строгой ∈{\displaystyle \in }-упорядоченности. Это утверждение называется парадоксом Бурали-Форти. Класс порядковых чисел обозначается различными способами: «Ord», «ON», или «∞».

Порядковое число конечно тогда и только тогда, когда оно вполне упорядочено не только естественным, но и противоположным порядком — это условие выполняется в том и только в том случае, когда каждое из его подмножеств содержит наибольший элемент.

Другие варианты определений[править | править код]

В современной математике существуют и другие подходы к определению порядковых чисел. Так, при выполнении аксиомы регулярности следующие утверждения относительно множества x являются эквивалентными:

x — порядковое число,
x — транзитивное множество с трихотомичным отношением ∈{\displaystyle \in }
x — транзитивное множество, линейно упорядоченное отношением ⊆{\displaystyle \subseteq }. Для множества X{\displaystyle X} определим двуместное отношение ϵ(X){\displaystyle \epsilon (X)}, состоящее из таких пар ⟨a,b⟩∈X2{\displaystyle \langle a,b\rangle \in X^{2}}, что a∈b{\displaystyle a\in b} или a=b{\displaystyle a=b}. Множество X{\displaystyle X} называется транзитивным, если из b∈X{\displaystyle b\in X} следует b⊆X{\displaystyle b\subseteq X}. Множество α{\displaystyle \alpha } называется ординалом, если оно транзитивно и ⟨α,ϵ(α)⟩{\displaystyle \langle \alpha ,\epsilon (\alpha )\rangle } — вполне упорядоченное множество.^[4]
x — транзитивное множество, элементы которого также являются транзитивными множествами.

Перечисленные определения неприменимы в теориях множеств без аксиомы фундирования. В теориях с урэлементами определения необходимо уточнить, поскольку урэлементы из числа элементов порядкового числа.

Трансфинитная последовательность[

Число с плавающей запятой — Википедия

Число с плавающей запятой (или число с плавающей точкой) — экспоненциальная форма представления вещественных (действительных) чисел, в которой число хранится в виде мантиссы и порядка (показателя степени). При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Используемое наиболее часто представление утверждено в стандарте IEEE 754. Реализация математических операций с числами с плавающей запятой в вычислительных системах может быть как аппаратная, так и программная.

«Плавающая запятая» и «плавающая точка»[править | править код]

Так как в некоторых, преимущественно англоязычных и англофицированных странах при записи чисел целая часть отделяется от дробной точкой, то в терминологии этих стран фигурирует название «плавающая точка» (англ. floating point). Так как в России целая часть числа от дробной традиционно отделяется запятой, то для обозначения того же понятия исторически используется термин «плавающая запятая», однако в настоящее время в русскоязычной литературе и технической документации можно встретить оба варианта.

Название «плавающая запятая» происходит от того, что запятая в позиционном представлении числа (десятичная запятая, или, для компьютеров, двоичная запятая — далее по тексту просто запятая) может быть помещена где угодно относительно цифр в строке. Это положение запятой указывается отдельно во внутреннем представлении. Таким образом, представление числа в форме с плавающей запятой может рассматриваться как компьютерная реализация экспоненциальной записи чисел.

Преимущество использования представления чисел в формате с плавающей запятой над представлением в формате с фиксированной запятой (и целыми числами) состоит в том, что можно использовать существенно больший диапазон значений при неизменной относительной точности. Например, в форме с фиксированной запятой число, занимающее 6 разрядов в целой части и 2 разряда после запятой, может быть представлено в виде 123 456,78. В свою очередь, в формате с плавающей запятой в тех же 8 разрядах можно записать числа 1,2345678; 1 234 567,8; 0,000012345678; 12 345 678 000 000 000 и так далее, но для этого необходимо иметь дополнительное двухразрядное поле для записи показателей степени основания 10 от 0 до 16, при этом общее число разрядов составит 8+2=10.

Скорость выполнения компьютером операций с числами, представленными в форме с плавающей запятой, измеряется во FLOPS (от англ. floating-point operations per second — «[количество] операций с плавающей запятой в секунду»), и является одной из основных единиц измерения быстродействия вычислительных систем.

Число с плавающей запятой состоит из следующих частей:

знак мантиссы (указывает на отрицательность или положительность числа),
мантисса (выражает значение числа без учёта порядка),
знак порядка,
порядок (выражает степень основания числа, на которое умножается мантисса).

Нормальная и нормализованная формы[править | править код]

Нормальной формой числа с плавающей запятой называется такая форма, в которой мантисса (без учёта знака) находится на полуинтервале [0 1), то есть 0 ⩽ a < 1.

Такая форма записи имеет недостаток: некоторые числа записываются неоднозначно (например, 0,0001 можно записать как 0,000001⋅10², 0,00001⋅10¹, 0,0001⋅10⁰, 0,001⋅10⁻¹, 0,01⋅10⁻² и так далее), поэтому распространена (особенно в информатике) также другая форма записи — нормализованная, в которой мантисса десятичного числа принимает значения от 1 (включительно) до 10 (исключительно), то есть 1 ⩽ a < 10 (аналогично мантисса двоичного числа принимает значения от 1 до 2). В такой форме любое число (кроме 0) записывается единственным образом. Недостаток заключается в том, что в таком виде невозможно представить 0, поэтому представление чисел в информатике предусматривает специальный признак (бит) для числа 0.

Старший разряд (целая часть числа) мантиссы двоичного числа (кроме 0) в нормализованном виде равен 1 (так называемая неявная единица), поэтому при записи мантиссы числа в ЭВМ старший разряд можно не записывать, что и используется в стандарте IEEE 754. В позиционных системах счисления с основанием большим, чем 2 (в троичной, четверичной и др.), этого свойства нет.

При ограниченных возможностях оформления (например, отображение числа на семисегментном индикаторе), а также при необходимости обеспечить быстрый и удобный ввод чисел, вместо записи вида m·b^e (m — мантисса; b — основание, чаще всего 10; e — экспонента), записывают лишь мантиссу и показатель степени, разделяя их буквой «E» (от англ. exponent). Основание при этом неявно полагают равным 10. Например, число 1,528535047⋅10⁻²⁵ в этом случае записывается как 1.528535047E-25.

Существует несколько способов того, как строки из цифр могут представлять числа:

Наиболее распространённый путь представления значения числа из строки с цифрами — в виде целого числа — запятая (radix point) по умолчанию находится в конце строки.
В общем математическом представлении строка из цифр может быть сколь угодно длинной, а положение запятой обозначается путём явной записи символа запятой (или, на Западе, точки) в нужном месте.
В системах с представлением чисел в формате с фиксированной запятой существует определённое условие относительно положения запятой. Например, в строке из 8 цифр условие может предписывать положение запятой в середине записи (между 4-й и 5-й цифрой). Таким образом, строка «00012345» обозначает число 1,2345 (нули слева всегда можно отбросить).
В экспоненциальной записи используют стандартный (нормализованный) вид представления чисел. Число считается записанным в стандартном (нормализованном) виде, если оно записано в виде aqn{\displaystyle aq^{n}}, где a{\displaystyle a}, называемое мантиссой, такое, что 1≤a<q{\displaystyle 1\leq a<q}, n{\displaystyle n} — целое, называется показатель степени и q{\displaystyle q} — целое, основание системы счисления (на письме это обычно 10). То есть в мантиссе запятая помещается сразу после первой значащей (не равной нулю) цифры, считая слева направо, а дальнейшая запись даёт информацию о действительном значении числа. Например, период обращения (на орбите) спутника Юпитера Ио, который равен 152 853,5047 с, в стандартном виде можно записать как 1,528535047⋅10⁵ с. Побочным эффектом ограничения на значения мантиссы является то, что в такой записи невозможно изобразить число 0.
Запись в форме с плавающей запятой похожа на запись чисел в стандартном виде, но мантисса и экспонента записываются раздельно. Мантисса записывается в нормализованном формате — с фиксированной запятой, подразумеваемой после первой значащей цифры. Возвращаясь к примеру с Ио, запись в форме с плавающей запятой будет 152853,5047 с показателем 5. Это означает, что записанное число в 10⁵ раз больше числа 1,528535047, то есть для получения подразумеваемого числа запятая сдвигается на 5 разрядов вправо. Однако, запись в форме с плавающей запятой используется в основном в электронном представлении чисел, при котором используется основание системы счисления 2, а не 10. Кроме того, в двоичной записи мантисса обычно денормализована, то есть запятая подразумевается до первой цифры, а не после, и целой части вообще не имеется в виду — так появляется возможность и значение 0 сохранить естественным образом. Таким образом, десятичная 9 в двоичном представлении с плавающей запятой будет записана как мантисса +1001000…0 и показатель +0…0100. Отсюда, например, беды с двоичным представлением чисел типа одной десятой (0,1), для которой двоичное представление мантиссы оказывается периодической двоичной дробью — по аналогии с 1/3, которую нельзя конечным количеством цифр записать в десятичной системе счисления.

Запись числа в форме с плавающей запятой позволяет производить вычисления над широким диапазоном величин, сочетая фиксированное количество разрядов и точность. Например, в десятичной системе представления чисел с плавающей запятой (3 разряда) операцию умножения, которую мы бы записали как

0,12 × 0,12 = 0,0144

в нормальной форме представляется в виде

(1,20⋅10⁻¹) × (1,20⋅10⁻¹) = (1,44⋅10⁻²).

В формате с фиксированной запятой мы бы получили вынужденное округление

0,120 × 0,120 = 0,014.

Мы потеряли крайний правый разряд числа, так как данный формат не позволяет запятой «плавать» по записи числа.

Диапазон чисел, представимых в формате с плавающей запятой[править | править код]

Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 1 бит знак + 52 бита, показатель — 1 бит знак + 10 бит. Таким образом получаем диапазон точности примерно от 4,94⋅10⁻³²⁴ до 1.79⋅10³⁰⁸ (от 2⁻⁵² × 2⁻¹⁰²² до ~1 × 2¹⁰²⁴). В стандарте IEEE 754 несколько значений данного типа зарезервировано для обеспечения возможности представления специальных значений. К ним относятся значения NaN (Not a Number, «не число») и +/-INF (Infinity, бесконечность), получающихся в результате операций деления на ноль или при превышении числового диапазона. Также сюда попадают денормализованные числа, у которых мантисса меньше единицы. В специализированных устройствах (например, GPU) поддержка специальных чисел часто отсутствует. Существуют программные пакеты, в которых объём памяти, выделенный под мантиссу и показатель, задаётся программно и ограничивается лишь объёмом доступной памяти ЭВМ (см. Арифметика произвольной точности).

Точность	Одинарная	Двойная	Расширенная
Размер (байты)	4	8	10
Число десятичных знаков	~7.2	~15.9	~19.2
Наименьшее значение (>0), denorm	1,4⋅10⁻⁴⁵	5,0⋅10⁻³²⁴	1,9⋅10⁻⁴⁹⁵¹
Наименьшее значение (>0), normal	1,2⋅10⁻³⁸	2,3⋅10⁻³⁰⁸	3,4⋅10⁻⁴⁹³²
Наибольшее значение	3,4×10⁺³⁸	1,7×10⁺³⁰⁸	1,1×10⁺⁴⁹³²
Поля	S-E-F	S-E-F	S-E-I-F
Размеры полей	1-8-23	1-11-52	1-15-1-63

S — знак, E — показатель степени, I — целая часть, F — дробная часть
Так же, как и для целых, знаковый бит — старший.

Машинный эпсилон[править | править код]

В отличие от чисел с фиксированной запятой, сетка чисел, которые способна отобразить арифметика с плавающей запятой, неравномерна: она более густая для чисел с малыми порядками и более редкая — для чисел с большими порядками. Но относительная погрешность записи чисел одинакова и для малых чисел, и для больших. Машинным эпсилоном называется наименьшее положительное число ε такое, что 1⊕ε≠1{\displaystyle 1\oplus \varepsilon \neq 1} (знаком ⊕{\displaystyle \oplus } обозначено машинное сложение). Грубо говоря, числа a и b, соотносящиеся так, что 1<ab<1+ε{\displaystyle 1<{\frac {a}{b}}<1+\varepsilon }, машина не различает.

Для одинарной точности ε=2−24≈5,96⋅10−8{\displaystyle \varepsilon =2^{-24}\approx 5,96\cdot 10^{-8}}, то есть, приблизительно 7 значащих цифр. Для двойной точности: ε=2−53≈1,11⋅10−16{\displaystyle \varepsilon =2^{-53}\approx 1,11\cdot 10^{-16}}, 15 значащих цифр^[1].

↑ E. Cheney, David Kincaid. Numerical Mathematics and Computing. — Cengage Learning, 2012. — 43– p. — ISBN 1-133-71235-5.

Криницкий Н. А., Миронов Г. А., Фролов Г. Д. Программирование. — М.: Государственное издательство физико-математической литературы, 1963. — 384 с.
Генри С. Уоррен, мл. Глава 15. Числа с плавающей точкой // Алгоритмические трюки для программистов = Hacker’s Delight. — М.: Вильямс, 2007. — С. 288. — ISBN 0-201-91465-4.

Комплексное число — Википедия

Запросы «Re», «Im» и «Мнимая величина» перенаправляются сюда; см. также другие значения терминов Re, Im и Мнимая величина.

Иерархия чисел

Ко́мпле́ксные чи́сла (от лат. complex — совокупный, тесно связанный^[1]; о двойном ударении см. примечание^{[K 1]}) — числа вида a+bi{\displaystyle a+bi}, где a,b{\displaystyle a,b} — вещественные числа, i{\displaystyle i} — мнимая единица^[2], то есть число, для которого выполняется равенство: i2=−1.{\displaystyle i^{2}=-1.} Множество комплексных чисел обычно обозначается символом C.{\displaystyle \mathbb {C} .} Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид a+0i{\displaystyle a+0i}. Главное свойство C{\displaystyle \mathbb {C} } — в нём выполняется основная теорема алгебры, то есть любой многочлен n{\displaystyle n}-й степени (n⩾1{\displaystyle n\geqslant 1}) имеет n{\displaystyle n} корней. Доказано^[⇨], что система комплексных чисел логически непротиворечива^{[K 2]}.

Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания^[⇨], умножения^[⇨] и деления^[⇨]. Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел; например, нельзя указать, какое из двух комплексных чисел больше или меньше^[⇨]. Удобно представлять комплексные числа a+bi{\displaystyle a+bi} точками на комплексной плоскости^[⇨]; например, для изображения сопряжённых чисел используется операция отражения относительно горизонтальной оси^[⇨]. Альтернативное представление комплексного числа в тригонометрической записи оказалось полезным для вычисления степеней и корней^[⇨]. Функции комплексного аргумента изучаются в комплексном анализе^[⇨].

Первоначально идея о необходимости использования комплексных чисел возникла в результате формального решения кубических уравнений, при котором в формуле Кардано под знаком квадратного корня получалось отрицательное число^[3]. Большой вклад в исследование комплексных чисел внесли такие математики, как Эйлер, который ввёл общепризнанное обозначение i{\displaystyle i} для мнимой единицы, Декарт, Гаусс^[⇨]. Сам термин «комплексное число» ввёл в науку Гаусс в 1831 году^[1].

Свойства комплексных чисел и функций нашли широкое применение для решения многих практических задач в различных областях математики, физики и техники: в обработке сигналов, теории управления, электромагнетизме, теории колебаний, теории упругости и многих других^[4]^[⇨]. Преобразования комплексной плоскости оказались полезны в картографии и гидродинамике. Современная физика полагается на описание мира с помощью квантовой механики, которая опирается на систему комплексных чисел.

Известно также несколько обобщений комплексных чисел — например, кватернионы^[⇨].

Связанные определения[править | править код]

Всякое комплексное число z=a+bi{\displaystyle z=a+bi} состоит из двух компонентов^[5]:

Противоположным для комплексного числа z=a+bi{\displaystyle z=a+bi} является число −z=−a−bi.{\displaystyle -z=-a-bi.} Например, для числа 1−2i{\displaystyle 1-2i} противоположным будет число −1+2i.{\displaystyle -1+2i.}

Четыре арифметические операции для комплексных чисел имеют те же свойства, что и аналогичные операции с вещественными числами. В отличие от последних, комплексные числа нельзя сравнивать на больше/меньше; доказано, что нет способа распространить порядок, заданный для вещественных чисел, на все комплексные так, чтобы порядок был согласован с арифметическими операциями (например, чтобы из a<b{\displaystyle a<b} вытекало a+c<b+c{\displaystyle a+c<b+c}). Однако комплексные числа можно сравнивать на равно/не равно)^[5]:

a+bi=c+di{\displaystyle a+bi=c+di} означает, что a=c{\displaystyle a=c} и b=d{\displaystyle b=d} (два комплексных числа равны между собой тогда и только тогда, когда равны их вещественные и мнимые части).

Сложение и вычитание[править | править код]

Определение сложения и вычитания комплексных чисел^[5]:

(a+bi)+(c+di)=(a+c)+(b+d)i,{\displaystyle \left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i,}

(a+bi)−(c+di)=(a−c)+(b−d)i.{\displaystyle \left(a+bi\right)-\left(c+di\right)=\left(a-c\right)+\left(b-d\right)i.}

Следующая таблица^[5] показывает основные свойства сложения для любых комплексных u,v,w.{\displaystyle u,v,w.}

Умножение[править | править код]

Определим произведение^[5] комплексных чисел a+bi{\displaystyle a+bi} и c+di{\displaystyle c+di}:

(a+bi)⋅(c+di)=ac+bci+adi+bdi2=(ac+bdi2)+(bc+ad)i=(ac−bd)+(bc+ad)i{\displaystyle (a+bi)\cdot (c+di)=ac+bci+adi+bdi^{2}=(ac+bdi^{2})+(bc+ad)i=(ac-bd)+(bc+ad)i}.

Следующая таблица^[5] показывает основные свойства умножения для любых комплексных u,v,w{\displaystyle u,v,w}.

Правила для степеней мнимой единицы:

i2=−1;i3=−i;i4=1;i5=i{\displaystyle i^{2}=-1;\;i^{3}=-i;\;i^{4}=1;i^{5}=i} и т. д.

Деление[править | править код]

Комплексное число z¯=x−iy{\displaystyle {\bar {z}}=x-iy} называется сопряжённым к комплексному числу z=x+iy{\displaystyle z=x+iy} (см. подробнее ниже).

Для каждого комплексного числа a+bi{\displaystyle a+bi}, кроме нуля, можно найти обратное к нему^[8] комплексное число 1a+bi{\displaystyle {\frac {1}{a+bi}}}. Для этого умножим числитель и знаменатель дроби на число a−bi{\displaystyle a-bi}, комплексно сопряжённое знаменателю

1a+bi=a−bi(a+bi)(a−bi)=a−bia2+b2=aa2+b2−ba2+b2i.{\displaystyle {\frac {1}{a+bi}}={\frac {a-bi}{(a+bi)(a-bi)}}={\frac {a-bi}{a^{2}+b^{2}}}={\frac {a}{a^{2}+b^{2}}}-{\frac {b}{a^{2}+b^{2}}}i.}

Определим результат деления^[5] комплексного числа a+bi{\displaystyle a+bi} на ненулевое число c+di{\displaystyle c+di}:

a+bic+di=(a+bi)(c−di)(c+di)(c−di)=ac+bdc2+d2+(bc−adc2+d2)i.{\displaystyle {\frac {a+bi}{c+di}}={\frac {\left(a+bi\right)\left(c-di\right)}{\left(c+di\right)\left(c-di\right)}}={\frac {ac+bd}{c^{2}+d^{2}}}+\left({\frac {bc-ad}{c^{2}+d^{2}}}\right)i.}

Как и для вещественных чисел, деление можно заменить умножением делимого на число, обратное к делителю.

Другие операции[править | править код]

Для комплексных чисел определены также извлечение корня, возведение в степень и логарифмирование.

Основные отличия комплексных чисел от вещественных[править | править код]

Уже упоминалось, что комплексные числа нельзя сравнивать на больше-меньше. Другое отличие: любой многочлен с вещественными или комплексными коэффициентами имеет, с учётом кратности, столько корней (вообще говоря, комплексных), какова его степень (основная теорема алгебры)^[9].

В системе вещественных чисел из отрицательного числа нельзя извлечь корень чётной степени. Для комплексных чисел возможно извлечение корня из любого числа любой степени, однако результат неоднозначен — комплексный корень n{\displaystyle n}-й степени из ненулевого числа имеет n{\displaystyle n} различных комплексных значений^[10]. См., например, корни из единицы.

Дополнительные отличия имеют функции комплексного переменного^[⇨]..

Замечания о выражении √−1[править | править код]

Заметим, что число i{\displaystyle i} не является единственным числом, квадрат которого равен −1{\displaystyle -1}. Число −i{\displaystyle -i} также обладает этим свойством.

Следует также заметить, что выражение −1{\displaystyle {\sqrt {-1}}}, ранее часто использовавшееся вместо i{\displaystyle i}, не вполне корректно, так как арифметический корень определяется только для неотрицательных чисел. Во избежание ошибок, выражение с квадратными корнями из отрицательных величин в настоящее время принято записывать как 5+i3{\displaystyle 5+i{\sqrt {3}}}, а не 5+−3{\displaystyle 5+{\sqrt {-3}}}, несмотря на то, что даже в XIX веке второй вариант записи считался допустимым^[11].

Пример возможной ошибки при неосторожном использовании устаревшей записи:

−3⋅−3=(−3)⋅(−3)=(−3)2=9=3{\displaystyle {\sqrt {-3}}\cdot {\sqrt {-3}}={\sqrt {\left(-3\right)\cdot \left(-3\right)}}={\sqrt {\left(-3\right)^{2}}}={\sqrt {9}}=3}.

При использовании современной записи такой ошибки не возникло бы:

(i3)⋅(i3)=(i⋅3)2=i2⋅(3)2=−3.{\displaystyle \left(i{\sqrt {3}}\right)\cdot \left(i{\sqrt {3}}\right)=\left(i\cdot {\sqrt {3}}\right)^{2}=i^{2}\cdot \left({\sqrt {3}}\right)^{2}=-3.}

Комплексная плоскость[править | править код]

$\left(i{\sqrt {3}}\right)\cdot \left(i{\sqrt {3}}\right)=\left(i\cdot {\sqrt {3}}\right)^{2}=i^{2}\cdot \left({\sqrt {3}}\right)^{2}=-3.$

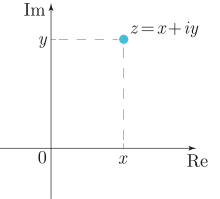Геометрическое представление комплексного числа

Комплексные числа можно представить на плоскости с прямоугольной системой координат: числу z=x+iy{\displaystyle z=x+iy} соответствует точка плоскости с координатами {x,y}{\displaystyle \left\{x,y\right\}} (а также радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется комплексной. Вещественные числа на ней расположены на горизонтальной оси, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями^[12].

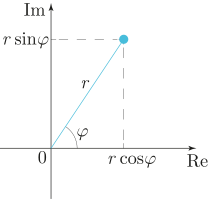$\left\{x,y\right\}$ Модуль r{\displaystyle r} и аргумент φ{\displaystyle \varphi } комплексного числа

Бывает удобно рассматривать на комплексной плоскости также полярную систему координат (см. рисунок справа), в которой координатами точки являются расстояние r{\displaystyle r} до начала координат (модуль^[⇨]) и угол φ{\displaystyle \varphi } радиус-вектора точки с горизонтальной осью (аргумент^[⇨]).

В этом представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов, а вычитанию чисел соответствует вычитание радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него соответствует повороту радиус-вектора первого числа на угол, равный аргументу второго числа^[13]. Этот факт объясняет широкое использование комплексного представления в теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза»^[14].

Пример: умножение на i{\displaystyle i} поворачивает радиус-вектор числа на прямой угол в положительном направлении, а после умножения на −i{\displaystyle -i} радиус-вектор поворачивается на прямой угол в отрицательном направлении.

Модуль[править | править код]

Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же самое, расстояние от точки комплексной плоскости до начала координат). Модуль комплексного числа z=x+iy{\displaystyle z=x+iy}

Арифметика — Википедия (с комментариями)

Ты — не раб!
Закрытый образовательный курс для детей элиты: «Истинное обустройство мира».
http://noslave.org

Материал из Википедии — свободной энциклопедии

Арифме́тика (др.-греч. ἀριθμητική; от ἀριθμός – число) — раздел математики, изучающий числа, их отношения и свойства. Предметом арифметики является понятие числа в развитии представлений о нём (натуральные, целые и рациональные, действительные, комплексные числа) и его свойствах. В арифметике рассматриваются измерения, вычислительные операции (сложение, вычитание, умножение, деление) и приёмы вычислений. Изучением свойств отдельных целых чисел занимается высшая арифметика, или теория чисел. Теоретическая арифметика уделяет внимание определению и анализу понятия числа, в то время как формальная арифметика оперирует логическими построениями предикатов и аксиом. Арифметика является древнейшей и одной из основных математических наук; она тесно связана с алгеброй, геометрией и теорией чисел^[1]^[2].

Причиной возникновения арифметики стала практическая потребность в счёте, простейших измерениях и вычислениях. Наука развивалась вместе с усложнением задач, требующих решения. Большой вклад в развитие арифметики внесли греческие математики, в частности философы-пифагорейцы, пытавшиеся с помощью чисел постичь и описать все закономерности мира.

В Средние века арифметику относили, вслед за неоплатониками, к числу так называемых семи свободных искусств. Основными областями практического применения арифметики тогда были торговля, навигация, строительство. В связи с этим особое значение получили приближённые вычисления иррациональных чисел, необходимые в первую очередь для геометрических построений. Особенно бурно арифметика развивалась в Индии и странах ислама, откуда новейшие достижения математической мысли проникли в Западную Европу; Россия знакомилась с математическими знаниями «и от греков, и от латин».

С наступлением Нового времени мореходная астрономия, механика, усложнившиеся коммерческие расчёты поставили новые запросы к технике вычислений и дали толчок к дальнейшему развитию арифметики. В начале XVII века Непер изобрёл логарифмы, а затем Ферма выделил теорию чисел в самостоятельный раздел арифметики. К концу века сформировалось представление об иррациональном числе как о последовательности рациональных приближений, а в течение следующего столетия благодаря трудам Ламберта, Эйлера, Гаусса арифметика включила в себя операции с комплексными величинами, приобретя современный вид.

Последующая история арифметики ознаменована критическим пересмотром её основ, попытками дедуктивного её обоснования. Теоретические обоснования представления о числе связаны в первую очередь со строгим определением натурального числа и аксиомами Пеано, сформулированными в 1889 году. Непротиворечивость формального построения арифметики была показана Генценом в 1936 году.

Основам арифметики издавна и неизменно уделяется большое внимание в начальном школьном образовании.

Предмет арифметики

Предметом арифметики являются числовые множества, свойства чисел и действия над числами^[3]. К ней также относят вопросы, связанные с техникой счёта, измерениями^[4], происхождением и развитием понятия числа^[1]. Арифметика изучает натуральные и рациональные числа, или дроби^[5]. На основе аксиоматической структуры множества натуральных чисел осуществляется построение других числовых множеств, включая целые, действительные и комплексные числа, проводится их анализ^[1]. Иногда в рамках арифметики рассматривают также кватернионы и другие гипер

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18