Классическая и ментальная арифметика: в чем разница | Статьи Академии AMAKids
На просторах Интернета активно обсуждается новая прогрессивная методика оттачивания интеллекта – ментальная арифметика. В крупных городах открываются развивающие центры для детей и взрослых, пополняется копилка рекордов скорости устных вычислений.
Многие родители ошибочно полагают, что методика развивает исключительно математические способности, не подходит для ребят с гуманитарным складом ума. Однако прохождение курса позволяет улучшить успеваемость не только по точным, но и по остальным школьным дисциплинам. Но существует ряд коренных различий между арифметикой в классическом понимании и ментальной.
Исторические данные
Арифметика – наука о числах и отношениях между ними. Первые сведения о таких знаниях датируются третьим-вторым тысячелетиями до нашей эры. Люди стали изучать свойства чисел, поскольку требовалось проводить измерения и считать.
Ментальная арифметика – более молодая методика, если рассматривать современную интерпретацию, но ее корни уходят глубоко, в то время, когда в Китае изобрели счеты абакус. Это произошло 5 тыс. лет назад. Сегодня устный счет на основе абакуса практикуется в 52 странах мира, а в Японии и Китае является частью программы общеобразовательных школ.
Процесс обучения
Изучение традиционной арифметики как части математики развивает логическое мышление. При этом активно задействуется левое мозговое полушарие. В процессе овладения ментальной арифметикой должную нагрузку получает правая половина мозга. Это дает возможность использовать не только логический подход к решению разных задач, но и творчество, интуицию. Такие способности выделяют из общей массы ученика, а впоследствии – специалиста.
Разница есть и в процессе обучения:
- в школе дети познают свойства чисел, отношения между ними посредством заучивания правил, порядка, алгоритмов выполнения арифметических действий;
- в ходе занятий ментальной арифметикой используются счеты (на первом этапе обучения), затем задачи решаются в уме. Дополнительные упражнения даются на специальных онлайн-платформах.
Глобальные отличия наблюдаются в результатах обучения. После усвоения основ арифметики в начальных классах учащиеся умеют выполнять сложение, вычитание, деление, умножение в столбик или путем разложения на разрядные единицы. Теоретически они считаются готовыми к постижению алгебры и геометрии, т. е. имеющими развитое логическое мышление. На практике эти более сложные дисциплины воспринимаются с огромными трудностями. Многие старшеклассники выходят из школьных стен, так и не полюбив математику.
После развивающих занятий с абакусом, тренировки одновременно обоих полушарий мозга слушатели решают в уме примеры любой сложности. У них увеличивается объем памяти, появляется способность к концентрации внимания, принятию нетрадиционных решений, повышается самооценка.
Противопоставлять обычную и ментальную арифметику не имеет смысла, эти понятия не заменяют друг друга. Авторская методика – полезное дополнение к школьному образованию.
Что такое арифметика и чем она отличается от математики?
С одной стороны это очень простой вопрос. С другой, школьники, да и многие взрослые, часто путают арифметику и математику и толком не знают в чем же разница между этими двумя предметами. Математика — это наиболее обширное понятие, которое включает в себя любые действия с числами. Арифметика же лишь один из разделов математики. К арифметике относятся знакомство с цифрами, простой счет и операции с числами. Раньше в школах уроки назывались именно арифметикой и лишь со временем стали носить название математика, которая плавно перетекает в алгебру. По сути алгебра начинается тогда, когда в примерах появляются неизвестные числа и вместо них используются буквы. То есть по-простому операции с x и y.
Термин «арифметика» произошел от греческого слова «arithmos», что означает «число». В 14-15 веках данный термин переводился в Англии не совсем верно — «the metric art», что по сути означало «метрическое искусство», подходящее больше для геометрии, нежели простого счета и несложных действий с числами.
Одна из причин, почему в школах не используется понятие «арифметика» заключается в том, что даже на уроках в начальных классах помимо цифр изучают также геометрические формы и единицы измерения (сантиметр, метр и т.д.), а это уже выходит за пределы обычного счета. Тем не менее, обучение ментальной арифметике происходит в жизни ребенка в какой-то степени само собой, в процессе знакомства с окружающим миром. Термин «ментальная арифметика» означает умение считать в уме. Согласитесь, каждый из нас в какой-то момент жизни учится этому и не только благодаря школьным урокам.
Сегодня есть целые методики для развития у детей навыков скоростного счета в уме. Например, особенно популярно древнее Абакус обучение, в основе которого лежит умение считать на специальных счетах (отличаются от обычных с десятками). Abacus
В арифметике используются четыре элементарные операции — сложение, вычитание, умножение и деление. Причем неважно целые числа используются в примере или же десятичные и дроби. Знакомить ребенка с цифрами можно еще с раннего детства, причем делать это непринужденно и в игре. В этом родителям поможет не только воображение, но и множество специальных развивающих материалов, найти которые можно в любом магазине.
По современным требованиям к первому классу ребенок должен уже считать минимум в пределе десяти (а лучше до 20), а также осуществлять со знакомыми цифрами основные операции — складывать их и вычитать. Важно также, чтобы ребенок мог сравнивать, какое из чисел больше, какое меньше, а какие числа равны. Таким образом, можно сказать, что именно арифметику ребенок должен знать еще до поступления в школу.
Такие требования предъявляются не только в России, но и во всем мире, т.к. темп жизни ускоряется, а объем знаний ежедневно увеличивается. То, что достаточно было знать в школьной программе еще 20-30 лет назад, сегодня занимает не более 50% преподаваемой учителями информации. Как бы там ни было, арифметика всегда останется основой основ для изучения цифр и счета, а также первоначальным уровнем математики, без которого невозможно изучить более сложные задания и умения.
Ментальная арифметика: формирование привычек и интеллекта
Ментальная арифметика(менар) –программа развития умственных и творческих способностей, основанная на системе устного счета с использованием счет- абакус (соробан ).
Подробнее с этой методикой Вы можете ознакомиться, прочитав статью на блоге «Ментальная арифметика — программа развития умственных и творческих способностей»
Я занимаюсь с детьми по программе «Ментальная арифметика». Мальчик перестал посещать занятия. Мама же объяснила, что применение английского они, как бы видят, а вот зачем нужна ментальная арифметика — не понимают.
Надо сказать, что ребенок очень напряженно относился к любому виду самостоятельных работ. Мы научились спокойно решать, не обращая внимания на результаты других, а фиксировали улучшение временных показателей при счете и на абакусе, и ментально.
Ребенку нравилось заниматься. А вот мама не увидела цели этих занятий — развитие интеллектуальных срособностей ребенка.
Взрослые отдают детей заниматься ментальной арифметикой, ориентируясь на название методики, а не на цели. Для понимания вопроса, стоит усвоить разницу между ментальной арифметикой и обычной арифметикой и математикой.
Постараюсь изложить, опуская многие педагогические, методические, психологические термины, что бы статья не показалась совсем занудной.
Ментальная арифметика и математика: сходства и различия.
АРИФМЕТИКА – ЧАСТЬ МАТЕМАТИКИ, но не заменяет математику.
В переводе с греческого языка «arithmos» обозначает «число». Арифметика – это раздел математики, в котором изучаются счет, числа и простые действия с ними. Изучение геометрических фигур, тел, отношений между числами выходит за рамки простейших операций, относится к математике в более широком смысле.
Ментальная арифметика – это нечто совершенно особенное. Ребенок, владеющий навыками быстрого счета в уме, не обязательно становится гением точных наук, но с большой вероятностью вырастает интеллектуалом, способным освоить любую профессию.
Основное отличие методики ментальной арифметик от школьного курса арифметики в том, что на занятиях по ментальной арифметикой дети не решают математические задачи, а используют навыки счета, составы чисел. Они выполняют упражнения, направленные на синхронное развитие обоих полушарий головного мозга.
Одна из целей курса – навык скоросчета. но он не является основной, так же как и скорочтение, быстрописание.
Развитие интеллектуальных способностей –цель, определяющая успех в развитии ребенка.
Задача методики ментальной арифметики — не в навыке быстрого счёта, а имеет более глубокий смысл: ментальная арифметика помогает натренировать нейронные связи головного мозга ребёнка, устойчиво развивает скорость и качество его мышления.
Умения и навыки скоросчета, скорочтение – полезные «побочные эффекты», который можно продемонстрировать, как натренированность работы головного мозга.
При разработке содержания программы «Ментальная арифметика» учтены следующие принципы, являющиеся основой и школьного курса «Математика»
1. Принцип открытости — не только давать знания, но еще и показывать их границы, «использовать в решении открытые задачи», т.е. задачи, стимулирующие самостоятельное генерирование идей, постоянное втягивание ребенка в принятие решений, в обсуждение касающихся его проблем.
Открытость — главное условие жизненности и перспективности — инновационности педагогических систем и концепций.
2. Принцип деятельности — освоение воспитанниками знаний, умений и навыков преимущественно в форме деятельности, направленной на решение проблем.
Учебная деятельность может возникнуть лишь там и тогда, когда цель обучения личностно значима для учащегося, «присвоена» им.
Учебная задача — это цель, личностно значимая для ученика, которая мотивирует изучение нового материала.
3. Принцип обратной связи — постоянный и системный контроль продвижения учащегося в своем обучении и развитии с помощью контрольно — диагностических мероприятий. Обратная связь направлена на повышение эффективности обучения учащихся. Обратная связь перенаправляет или фокусирует образовательный процесс на совместные действия учителя и учащихся в достижения учебных целей и ориентирует на конкретный результат.
4. Принцип идеальности — максимально использовать возможности, знания, интересы самих воспитанников с целью повышения результативности и уменьшения затрат в процессе освоения знаний, использование новых методов для решения задач, учитывающие конкретные особенности конкретных систем, а так же индивидуадьные особенности, связанные с личностью конкретного человека.
Эти принципы заложены и в изучение математики стандартного школьного курса. Эти принципы работают в курсе «Ментальная арифметика».
Попробуем разобраться.
Предмет математики — то, что изучает математика как наука, выраженное в наиболее общей форме. Одно из возможных определений предмета математики — это изучение систем математических объектов.
Матема́тика (др.-греч. μᾰθημᾰτικά[1]
Известны два подхода к определению предмета математики. Одно определение дано Ф.Энгельсом, другое – коллективом французских математиков под общим псевдонимом Н.Бурбаки.
Согласно Ф. Энгельсу, «чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира, стало быть, – весьма реальный материал. Тот факт, что этот материал принимает чрезвычайно абстрактную форму, может лишь слабо затушевывать его происхождение из внешнего мира». Хотя это предложение нельзя считать полным определением математики, поскольку оно не указывает метод, цели изучения математики, но отражает то, что объект изучения создан умом человека не произвольно, а в связи с реальным миром.
Второй подход отражает методологические установки Н. Бурбаки, которые также определяют не математику, а только объекты, которые она исследует. Прежде чем привести их определение, отметим, что новый подход к объектам исследования в математике связан с «революцией в аксиоматике». Суть ее состоит в переходе от конкретной содержательной аксиоматики к аксиоматике сначала абстрактной, а затем полностью формализованной.
Трудно говорить о сходствах и различиях, не имея четких определений предметов обсуждения: математика и ментальная арифметика, и имея только абстрактную форму.
Но я думаю, что преподавая предмет «Математика» более 40 лет, у меня сложилось четкое представление об этом предмете, о его содержании, методах изучения и методике преподавания, что и позволяет мне, с уверенностью, утверждать, что предмет «Ментальная арифметика» — это не «Математика», это арифметика.
Над одними и теми же примерами в ментальной арифметике работают достаточно долго. Например, при сложение однозначных чисел работаем визуально, на слух, на абакусе, ментально, сначала в пределах пяти, затем «переходя» через пятёрку. Нарабатывая устойчивую нейронную связь: шевеля пальчиками, мысленно передвигаем костяшки абакуса.
Повторяемость – вот один из секретов эффективности ментальной арифметики.
Ментальная арифметика – это сложно, это годы тренировок. На первом году обучения ребенок получает только примеры на сложение и вычитание. И только на втором году обучения – на умножение и деление. При работе ребенок использует только большой и указательный пальцы. Все движения доводятся до автоматизма.
В Китае и Японии не гонятся за результатом – скорее научить ребенка быстро считать, сделать видео, выложить в ютуб. Там дети годами сидят и оттачивают свои навыки. Годами. У нас же родители хотят скорее увидеть результат, хотят вау-эффекта. .И так постепенно отрабатываем правила сложения и вычитания чисел, доводя до автоматизма при счете на абакусе, а затем и ментально, увеличивая скорость вычисления, подключая дополнительные «помехи» в виде пения песен, чтения стихов. И когда все это срабатывает, мы получаем нужный визуальный результат.
А что творится в голове? Какие мыслительные процессы происходят во время счета?
Самое интересное то, что начав заниматься, большинство детей не бросают занятия, значит они «чувствуют» изменения в себе и нужность этого предмета.
Ментальная арифметика и школьная математика – совсем разные предметы.
Ребенок не начнет сразу получать отличные оценки по математике, но он, безусловно, начнет со временем лучше успевать в школе. Потому что он станет более внимательным, научится концентрироваться, у него улучшится память. В итоге и по математике, в том числе, станут лучше оценки. Но вовсе не потому, что он начнет в школе считать ментально, нет!
–Что ментальная арифметика может помешать школьной математике?
– Так не получится. Это совершенно разные системы. С помощью правил ментальной арифметики ребенок просто не сможет решить многие математические школьные примеры.
А теперь поумничаем, ибо без некоторых понятий работы головного мозга нам всё равно не обойтись.
Речь пойдет о временных связях в коре головного мозга, формирующихся при запоминании.
Нейронные связи и формирование привычек и интеллекта.
Я очень поверхностно, буквально в двух словах, скажу, как наш мозг создает нейронные связи и формирует привычки и интеллект.
Любые новые нейронные цепочки являются весьма хрупкими по сравнению со старыми. Когда вы сможете понять, как трудно создаются в мозгу человека новые нейронные пути, вы будете радоваться настойчивости вашего ребенка в этом направлении больше, чем ругать ребенка за медленный прогресс в их формировании.
На сознательном уровне вы не можете решать, какие именно синаптические связи вам следует развивать. Они формируются двумя основными способами:
1) Постепенно, путем многократного повторения.
2) Одномоментно, под воздействием сильных эмоций.
Из истории.

Межполушарное взаимодействие ТЕКСТ
Коллектив авторов
Из серии: Учебник XXI века (Генезис)
Раздел 5 посвящен онтогенетическим аспектам межполушарных взаимодействий человека. В определенном смысле они отражают эволюцию, преемственность нейропсихологического знания о закономерностях формирования межполушарных взаимодействий в онтогенезе и центральной роли стволовых и срединных образований.
Из справочника.

Другим аспектом функционирования мозга, имеющим последствия для когнитивного развития, является латеризация. Дети используют обе руки при работе с абакусом и визуализируют его, в результате чего учатся визуализировать цифры в форме косточек абакуса и выполняют все операции при помощи визуальных образов.
Из учебника
Несмотря на свидетельства в пользу Л. г. м. чел., последний, находясь в нормальном состоянии, работает согласованно и как единое целое. Кинсборн указывает, что латерализованное функционирование одногополушария является комплементарным по отношению к функционированию другого. Л. г. м. яв-ся скорее средством обработки различных компонентов информации, чем механизмом осуществления различных видов деятельности.
Американский ученый М. Кинсборн считает, что бедность правого полушария лишает их творческого импульса. Опираясь только на логику, невозможно создать что-либо по-настоящему новое. Запаздывание левополушарной латерализации обусловливает различные задержки психического развития. Неспособность к 6—7 годам усвоить букву и цифру, отсутствие естественного интереса к ним делает проблематичным обучение в школе.
( Из Визель Т.Г. Основы нейропсихологии: учеб. для студентов вузов Т.Г. Визель . — М.: АСТАстрель Транзиткнига, 2005.- 384,(16)с.- (Высшая школа)
Ментальная арифметика развивает и левое и правое полушарие, что позволяет улучшить академическую успеваемость детей, освоение всех школьных дисциплин.
КАК ВЛИЯЮТ ЗАНЯТИЯ МЕНТАЛЬНОЙ АРИФМЕТИКОЙ НА УСПЕВАЕМОСТЬ
Если при изучении курса ментальной арифметики, поставленные задачи были достигнуты, дети демонстрируют навыки совершения простых и сложных действий с числами в уме, без бумаги и калькулятора, с большой скоростью, то, с большой уверенностью можно сказать, что развиты и следующие навыки:
-цепкая память;
-логическое мышление, воображение;
— умение абстрагироваться;
-уверенность в себе, своих силах;
-высокая способность и мотивация к обучению.
Занятия ментальной арифметикой помогают лучшему усвоению курса математики, но никак его не заменяют. Форматы обучения имеют разные цели и методологические основы.
Практические результаты применения этого метода доказывают, что обучение ментальной арифметике с помощью абакуса, повышают интеллект, умственные способности, что положительно влияет на успешное освоение точных наук, быстрому запоминанию большого количества слов, текстов, дат, необходимых при изучении иностранных языков, истории, то есть гуманитарных наук.
Занятия, задействующие оба полушария головного мозга, закладывают навыки и умения, которые будут использоваться всю жизнь: .-способность к освоению иностранных языков;
-повышенная фокусировка и концентрация внимания, быстрое мышление и скорость реакции;
— фотографическая память; слуховая память;
— развитое воображение, креативное мышление;
-навыки, необходимые для эффективной работы в условиях многозадачности;
— самостоятельность, уверенность в своих силах, способность быстро принимать решения.
На начальных этапах занятий ментальной арифметикой, примерно в течение года, используется абакус (счеты),а в дальнейшем дети производят вычисления в уме, создавая мысленный образ абакуса. Занятия проходят 1 раз в неделю и длятся по 2 академических часа. Кроме того, детям предстоит выполнять ежедневно домашние задания, что занимает 15-20 минут.
При работе ребенок использует только большой и указательный пальцы. Все движения доводятся до автоматизма. Через некоторое время ребенок совершает вычисления на воображаемом абаке, а задачи решаются с помощью образов.
Для быстрого счета в уме ребенок учится запоминать и мгновенно «воспроизводить» в уме «картинку» определенного числа в виде положения костяшек на абакусе. Таким образом, тренируется визуальная фотографическая память, увеличивается «объем» памяти, повышается способность к быстрому запоминанию.
Но надо стремиться увлечь ребенка и дать ему мотивацию к тренировкам.
Каждый ребенок уникален. Не бойтесь пробовать новые, прогрессивные способы развития мышления ребенка, и вы увидите, каких высот он сможет достичь.
В чем заключается формула интеллекта? Логика плюс интуиция.
Развитие детского интеллекта – формирование способности к адаптации, обучению, пониманию абстрактных понятий, планированию, постановке и достижению целей. Все эти качества эффективно развиваются, благодаря ментальной арифметике. Особенно результативны занятия в дошкольном возрасте.
Мышление – познавательная деятельность, способность анализировать, синтезировать, сравнивать, обобщать, выполнять другие познавательные операции. Можно сказать, что интеллектуал – человек с развитым мышлением, поэтому совершенствование интеллекта – задача более широкая.
На занятиях ментальной арифметикой дети работают с воображаемыми счетами, начинают воспринимать математические задачи как картинки, активно включая в работу правое полушарие головного мозга. В процессе выполнения упражнений совершенствуются центры, отвечающие за интеллектуальные способности.
На уроках ментальной арифметики, путем многократного повторения, работая пальчиками, подключая оба полушария, мы и пытаемся создать устойчивые синаптические связи.
«»Можно ли увидеть эту работу? Можно ли увидеть сразу результат такой работы? «»»
Это новые нейронные пути работы головного мозга.
Это применимо только в арифметике, математике? Нет! Мозг будет использовать эти пути в любых ситуациях!
Простите меня, за утрированную простоту изложения, но мне хочется объяснить родителям, что результат освоения навыков ментального счета-процесс не быстрый, а научить считать ребенка быстрее калькулятора-не цель, а только один из показателей работы головного мозга.
Формируем интеллект. Но ни кто и не говорит, что получатся ИНДИГО.
Как мы уже знаем, что левое полушарие отвечает за логику, рациональность и анализ, а правое – за образность, целостность, интуицию, фантазию и воображение. Возникает вопрос – как развить взаимосвязь работы обоих полушарий, чтобы максимально раскрыть потенциал ребенка?
Программа обучения метальной арифметики направлена на формирование устойчивых нейронных связей левого и правого полушарий. Этот факт помогает людям выбирать наиболее эффективные решения и добиваться успеха в жизни.
Математические и логические задачи активизируют мозг, развивают навыки мышления. Они учат творческому мышлению — поиску нестандартных решений или тому, что правильных решений у задачи может быть несколько.
В группе нет оценок и соревнований между учениками. Общение с преподавателем строится на равных.
Каждый ученик настраивается только на улучшение собственных результатов.
В начале работы группа согласовывает правила поведения. Любая активность и общение, которые не противоречат правилам и не мешают занятиям, разрешены. Занятия проходят в доброжелательной оживленной атмосфере.
Необходимость самостоятельно тренироваться не только закрепляет и развивает навык быстрого счета, но и приучает подростка к ответственности: заниматься каждый день, невзирая на внешние обстоятельства и перепады настроения). Привычка к методичности и самодисциплина распространяются на все сферы жизни подростка.
Хороших результатов в освоении программы можно достичь:
— при методичном освоении и отработке навыков счета от простого к сложному;
-при ежедневном выполнении домашнего задания;
-при проведении систематических соревнований, в которых каждый ученик отмечает свой прогресс.
Менар – это одна из методик развития интеллекта, которая помогает выявить и раскрыть уникальные способности ребенка. Ребенок учится быстро усваивать новую информацию, формулировать мысли и делать выводы. Тем не менее, не стоит пренебрегать традиционными играми – шахматами, головоломками, ребусами.
Поэтому, наблюдайте, пробуйте, анализируйте и выбирайте то, что подходит именно вам.
Как подготовить ребенка по математике к школе и к занятиям по ментальной арифметике, можно почитать на моей странице «Математика дома» в фейсбуке. https://www.facebook.com/pg/kat1j/posts/?ref=page_internal
Спасибо за посещение моего блога. Выскажите, пожалуйста, своё мнение в комментариях.
Я обучаюсь в социальном проекте «Одна семья». И очень заинтересована в любых ваших высказываниях, которые помогут мне в дальнейшей работе.Чем ментальная арифметика отличается от методики Марии Монтессори
Растущий интерес к раннему развитию детей порождает избыток предложения. На рынке образовательных услуг развивающих курсов хоть пруд пруди, но не все они одинаково полезны. Инновационная педагогика Марии Монтессори и ментальная арифметика – неизменные фавориты родителей и педагогов.
Методика Монтессори: школа свободного ребенка
Детский врач, педагог и психолог Мария Монтессори утверждала, что ребенку для успешного обучения вообще не нужна школа. Взаимодействуя с окружающей средой, малыш усваивает знания легко и непринужденно. Задача педагога сводится к созданию подготовленной среды с открытым доступом к разнообразным дидактическим материалам, имитирующим реальные предметы. Оптимальным для начала занятий считается дошкольный возраст – от 2 до 6 лет.
К игрушкам и сюжетным играм Монтессори относилась настороженно, полагая, что они погружают ребенка в искусственную среду и тем самым ограничивают возможности познания мира. Современные данные утверждают обратное, поэтому в большинстве Монтессори-групп предусмотрены игровые комнаты.
Классы Монтессори разделены на пять тематических зон:
- зона математики – здесь собраны пособия, наглядно разъясняющие количественные и пространственные понятия, логические головоломки, макеты геометрических фигур;
- зона языков – показывает детям буквы и слоги, помогает выработать навыки письма и чтения;
- зона практической жизни – объединяет дидактические материалы, воспитывающие навыки самообслуживания путем подражания взрослым. Малыши учатся ухаживать за собой, стирать и гладить одежду, готовить, мастерить и убирать дом;
- сенсорная зона – учит различать характеристики различных предметов: форму, цвет, размер, вес, а также стимулирует развитие чувственного восприятия, памяти и мелкой моторики;
- зона космоса – знакомит детей с устройством мира, законами природы и культурой разных народов.
Дети свободно перемещаются по классу и могут использовать любые материалы по собственному усмотрению. Каждый ученик обучается в органичном для него темпе, не испытывая стресса из-за конкуренции с другими ребятами, здесь не ставят оценок и не ругают за неуспеваемость. Монтессори-группы часто посещают разновозрастные дети, которые совершенно не мешают друг другу; активно поощряется помощь младшим.
Вмешательство учителя допустимо только по инициативе ребенка. Если малыш выбрал забаву явно не по возрасту, можно попытаться переключить его внимание на предметы, более соответствующие специфике того или иного сензитивного периода. Мария Монтессори была убеждена, что соблюдение принципа автономии ребенка воспитывает в детях дисциплину и самостоятельность намного эффективнее репрессивных мер.
Ментальная арифметика – тренажер для мозга
Обычно на курсы ментальной арифметики в наш центр интеллектуального развития для детей и взрослых приводят детей, испытывающих трудности со счетом, письмом и чтением. Разумеется, мы помогаем им подтянуться. Вместе с тем умение быстро считать в уме, бегло читать, легко запоминать огромные объемы информации и писать без ошибок для нас не самоцель, а всего лишь упражнения для тренировки мозга, которых известно великое множество. К примеру, обучение скорочтению также способствует развитию когнитивных способностей и улучшению успеваемости. Все намного сложнее и интереснее!
Регулярные занятия ментальной арифметикой устраняют функциональную асимметрию мозга, которая возникает из-за привычки обращаться только к левому полушарию, ответственному за логику, анализ и вербальный интеллект. Традиционный подход к обучению совершенно игнорирует невербальное правое полушарие, воспринимающее мир сквозь призму образов и эмоций. Так мы привыкаем думать и жить вполсилы, оставаясь на обочине успеха. Занимаясь в группах ментальной арифметики, дети привыкают включать мозг на полную мощность и существовать в полной гармонии с собой и миром.
Ментальная арифметика – универсальная методика, которая подходит всем без исключения, от мала до велика. Оптимальное время для начала занятий – от 5 до 12 лет. К новичкам не предъявляется особых требований: достаточно уметь считать до десяти.
Курс ментальной арифметики строится по схеме «от простого к сложному». Для начала детей знакомят с техникой вычислений с помощью абакуса, соотнося разноцветные костяшки с визуальными образами, подключающими к работе правое полушарие. Поскольку при этом задействуются три вида памяти – зрительная, моторная и смысловая, новый материал усваивается намного быстрее. Далее, по мере наработки навыков, использование абакуса постепенно сходит на нет, а под конец все вычисления производятся в уме.
Игровой формат занятий избавляет ребенка от стресса и помогает поверить в свои силы. Для самых продвинутых учеников мы проводим соревнования, но соревнуемся исключительно ради удовольствия, не разделяя детей на лидеров и аутсайдеров. На самом деле все ребята талантливы, просто некоторые еще об этом не знают.
Как видите, ментальная арифметика и педагогическая система Монтессори не идентичны друг другу, так как строятся на разных принципах и активируют разные нейропсихологические механизмы. За каждым подходом стоит целостная дидактическая система, хотя одно не исключает другое. Занятия ментальной арифметикой можно совмещать с посещением Монтессори-групп.
Что плохого в ментальной арифметике? | Материнство
Изначально ментальная арифметика использовалась японскими торговцами для быстрых расчетов со своими покупателями. Не случайно в ней используется абакус, старинный аналог калькулятора.
Абакус содержит четыре костяшки на каждой линеечке и отдельно костяшку, обозначающую пятерку. Таким образом, любое число до 10 может быть обозначено как набор единиц, либо как пятерка и ещё сколько-то единиц.

От привычных счётов с десятью костяшками в ряду, которые и сейчас ещё можно увидеть в магазинах, абакус отличается тем, что помимо структуры числа в десятичной системе, одновременно добавляется структура внутри десятка. Чем нам помогает деление на пятерки? Это заставляет нас считать так, как если бы мы считали на пальцах. Это делает расчёты молниеносными. То есть абакус идеально подходит торговцам, как и было задумано.
Спорный инструмент обучения
Адепты ментальной арифметики преподносят её как подходящий детям способ освоить устный счёт на «отлично». Так ли это? Скорее нет.
Обучение, в отличие от бытовой задачи быстрого расчёта, подразумевает, что нужно научить ребёнка понимать, как он считает. Любое понимание математики – это освоение математических понятий, которые подаются через наглядные пособия, затем иллюстрации и затем абстрактные образы. В ментальной арифметике всё так – счёты с костяшками, затем мнемонические карточки, затем счёт в уме. Но проблема в том, что ученику даётся только один алгоритм и не предлагается вообще никаких других моделей, кроме абакуса.
Кроме того, ментальная арифметика предполагает, что ребёнок уже умеет быстро раскладывать в уме семь как 5+2, девять как 5+4, знает состав всех чисел, может легко сложить 8 и 5, разложив 5 на 2 и 3, и прибавив 3 к 10.
Нет наглядного изучения состава чисел до 10, только до 5, а от 6 до 10 приходится зубрить, что совсем нездорово. Ментальная арифметика не дает понимания арифметических действий, ее цель – получение быстрого ответа.
Недостатки раннего обучения
Предположим, что ребёнок научился быстро считать до семи лет с помощью ментальной арифметики. Что происходит дальше? Он попадает в школу, объяснения учителя ему уже не интересны, потому что считает он быстро – и шансов понять математику очень мало.
Ментальная арифметика не дает возможности делать приближенные вычисления, так как ребенок будет автоматически обращаться к одному алгоритму, который для него прост и понятен. В то время как в жизни требуется гибкость, использование разных способов эффективного счёта. Хороший устный счёт означает, что сначала мы выбираем метод счёта, который лучше подойдёт в данном случае.
Помните про взаимосвязь математических операций и их многомерность
Ребёнку, рано освоившему ментальную арифметику, будет сложнее понять, что существует не только десятичная система строения числа, но и двоичная, восьмеричная, двенадцатеричная и так далее. Привязка к десятичной системе значительно усложнит жизнь ученика в дальнейшем.
Также этот метод хуже готовит к освоению корней, степеней, логарифмов. Он делает трудным освоение дробей, переход от десятичных дробей к обычным. Десятичные дроби после ментальной арифметики даются легко, а вот обычные дроби – одна из основополагающих тем школьной программы — станут проблемой.
Лобные доли, которые отвечают в мозгу за функции программирования и контроля, окончательно созревают к 20 годам. Даже в 10 лет они находятся в стадии формирования. Поэтому та нагрузка, которую дает на мозг ментальная арифметика, для детей начальной школы, а тем более дошкольников, может оказаться чрезмерной.
Урок математики в школе. Фото — фотобанк Лори
И все же – когда ментальная арифметика полезна?
Обучать детей ментальной арифметике до школы я бы точно не рекомендовала. Это может быть полезно тем детям, которые уже в школе испытывают трудности. Знание этого метода даст им уверенность и свободу в вычислениях. При этом школьную программу ментальной арифметикой лучше не предварять и не обгонять. Она может быть также полезной в 3-4 классах, когда в школе проходят умножение в столбик.
Ментальная арифметика может помочь детям 9-11 лет, когда они уже обладают определенными навыками и знанием, но столкнулись с какими-то трудностями или отстали.
Абакус полезен тем, что он нагляден, ребёнок может «посчитать руками». Она также развивает функции программирования и контроля: нам нужно сделать одну операцию в рамках другой, помнить предварительный результат, использовать его в следующей операции и так далее. Это даёт высокую нагрузку на рабочую память, на зрительно-пространственные функции и это неплохо.
Вообще же я скорее бы рекомендовала ментальную арифметику пожилым людям, просто как гимнастику для мозга.
Ментальная арифметика и школьная математика – есть ли связь? | Статьи Академии AMAKids

Дети по-разному относятся к школьному курсу математики. Одни влюбляются в цифры с первого знакомства, другие считают предмет сложным, скучным, сухим. Плохая успеваемость по базовой школьной дисциплине всегда беспокоит родителей.
Для исправления ситуации взрослые отдают детей заниматься ментальной арифметикой, ориентируясь на название методики, а не на цели. Для понимания вопроса стоит усвоить разницу между обычной арифметикой и математикой.
Арифметика – часть математики
В переводе с греческого языка «arithmos» обозначает «число». Арифметика – это раздел математики, в котором изучаются счет, числа и простые действия с ними. Изучение геометрических фигур, тел, отношений между числами выходит за рамки простейших операций, относится к математике в более широком смысле.
Ментальная арифметика – это нечто совершенно особенное. Ребенок, владеющий навыками быстрого счета в уме, не обязательно становится гением точных наук, но с большой вероятностью вырастает интеллектуалом, способным освоить любую профессию.
Условие приема на занятия ментальной арифметикой – умение считать до десяти. Требования к первоклассникам, поступающим в школу, гораздо шире:
- распознавание основных геометрических фигур;
- ориентирование в понятиях «больше», «меньше»;
- умение производить арифметические действия и прочее, в зависимости от уровня общеобразовательного учебного заведения.
Минимальная степень начальной подготовки – ключевое отличие методики от школьного подхода. На занятиях ментальной арифметикой дети не решают математические задачи. Они выполняют упражнения, направленные на синхронное развитие обоих полушарий головного мозга. Одна из целей курса – навык скоросчета. Он не является основным. Развитие интеллектуальных способностей – глобальная цель, определяющая успех в освоении всех школьных дисциплин.
Как влияют занятия ментальной арифметикой на успеваемость
Если ментальная арифметика изучалась на специализированных курсах, и поставленные задачи были достигнуты, дети демонстрируют навыки совершения простых и сложных действий с числами в уме, без бумаги и калькулятора, с большой скоростью.
Кроме этого, у них повышается интеллект, умственные способности, что положительно влияет на успешное освоение точных наук, включенных в школьную программу. Этому содействуют:
- цепкая память, развитое логическое мышление, воображение;
- умение абстрагироваться;
- уверенность в себе, своих силах;
- высокая способность и мотивация к обучению.
Вывод из сказанного: занятия ментальной арифметикой помогают лучшему усвоению курса математики, но никак его не заменяют. Форматы обучения имеют разные цели и методологические основы.
Арифметика — Википедия

Арифме́тика (др.-греч. ἀριθμητική, arithmētikḗ — от ἀριθμός, arithmṓs «число») — раздел математики, изучающий числа, их отношения и свойства. Предметом арифметики является понятие числа (натуральные, целые, рациональные, вещественные, комплексные числа) и его свойства. В арифметике рассматриваются измерения, вычислительные операции (сложение, вычитание, умножение, деление) и приёмы вычислений. Изучением свойств отдельных целых чисел занимается высшая арифметика, или теория чисел. Теоретическая арифметика уделяет внимание определению и анализу понятия числа, в то время как формальная арифметика оперирует логическими построениями предикатов и аксиом. Арифметика является древнейшей и одной из основных математических наук; она тесно связана с алгеброй, геометрией и теорией чисел[1][2].
Причиной возникновения арифметики стала практическая потребность в счёте и вычислениях, связанных с задачами учёта при централизации сельского хозяйства. Наука развивалась вместе с усложнением задач, требующих решения. Большой вклад в развитие арифметики внесли греческие математики — в частности, философы-пифагорейцы, пытавшиеся с помощью чисел постичь и описать все закономерности мира.
В Средние века арифметику относили, вслед за неоплатониками, к числу так называемых семи свободных искусств. Основными областями практического применения арифметики тогда были торговля, навигация, строительство. В связи с этим особое значение получили приближённые вычисления иррациональных чисел, необходимые, в первую очередь, для геометрических построений. Особенно бурно арифметика развивалась в Индии и странах ислама, откуда новейшие достижения математической мысли проникли в Западную Европу; Россия знакомилась с математическими знаниями «и от греков, и от латин».
С наступлением Нового времени мореходная астрономия, механика, усложнившиеся коммерческие расчёты выдвинули новые требования к технике вычислений и дали толчок к дальнейшему развитию арифметики. В начале XVII века Непер изобрёл логарифмы, а затем Ферма выделил теорию чисел в самостоятельный раздел арифметики. К концу века сформировалось представление об иррациональном числе как о последовательности рациональных приближений, а в течение следующего столетия благодаря трудам Ламберта, Эйлера, Гаусса арифметика включила в себя операции с комплексными величинами, приобретя современный вид.
Последующая история арифметики ознаменована критическим пересмотром её основ, попытками дедуктивного её обоснования. Теоретические обоснования представления о числе связаны, в первую очередь, со строгим определением натурального числа и аксиомами Пеано, сформулированными в 1889 году. Непротиворечивость формального построения арифметики была показана Генценом в 1936 году.
Основам арифметики издавна и неизменно уделяется большое внимание в начальном школьном образовании.

Предметом арифметики являются числовые множества, свойства чисел и действия над числами[3]. К ней также относят вопросы, связанные с техникой счёта, измерениями[4], происхождением и развитием понятия числа[1]. Арифметика изучает, в первую очередь, натуральные числа и дроби[5]. На основе аксиоматической структуры множества натуральных чисел осуществляется построение других числовых множеств, включая целые, действительные и комплексные числа, проводится их анализ[1]. Иногда в рамках арифметики рассматривают также кватернионы и другие гиперкомплексные числа. Вместе с тем, из теоремы Фробениуса следует, что расширение понятия числа за пределы комплексной плоскости без потери каких-либо его арифметических свойств невозможно[6][7].
К основным действиям над числами относят сложение, вычитание, умножение и деление[3], реже — возведение в степень, извлечение корня[4] и решение численных уравнений[3]. Исторически список арифметических действий также включал собственно счёт, удвоение (помимо умножения), деление на два и деление с остатком (помимо деления), поиск суммы арифметической и геометрической прогрессий[8]. Джон Непер в своей книге «Логистическое искусство» разделил арифметические действия по ступеням: на низшей ступени находятся сложение и вычитание, на следующей — умножение и деление, далее — возведение в степень и извлечение корней[9]. Известный методист И. В. Арнольд к операциям третьей ступени относил также логарифмирование[10]. Традиционно арифметикой называют выполнение операций над различными объектами, как то: «арифметика квадратичных форм», «арифметика матриц»[1].
Собственно математические расчёты и измерения, необходимые для практических нужд (пропорции, проценты, тройное правило), относят к низшей, или практической арифметике[3], в то время как логический анализ понятия числа относят к теоретической арифметике[1]. Свойства целых чисел, деление их на части, построение непрерывных дробей являются составной частью теории чисел[1], которую долгое время считали высшей арифметикой[3]. Арифметика также тесно связана с алгеброй, которая изучает собственно операции без учёта особенностей и свойств чисел[1][11]. Такие арифметические действия, как возведение в степень и извлечение корней, являются технической частью алгебры. В этой связи, вслед за Ньютоном и Гауссом, алгебру принято считать обобщением арифметики[3][4]. Вообще говоря, чётких границ между арифметикой, элементарной алгеброй и теорией чисел не существует. В БСЭ сказано: «Алгебра изучает, пользуясь буквенными обозначениями, общие свойства числовых систем и общие методы решения задач при помощи уравнений; арифметика занимается приёмами вычислений с конкретно заданными числами, а в своих более высоких областях (см. Чисел теория) — более тонкими индивидуальными свойствами чисел»[12].
Как и прочие академические дисциплины, арифметика сталкивается с принципиальными методологическими проблемами; для неё необходимо исследование вопросов непротиворечивости и полноты аксиом[3]. Логическими построениями формальной системы предикатов и аксиом арифметики занимается формальная арифметика[2].
Порядковый счёт, натуральные числа[править | править код]
 Одно яблоко, два яблока, три яблока. Натуральные числа
Одно яблоко, два яблока, три яблока. Натуральные числаПростейшим арифметическим понятием является порядковый счёт. Объектом счёта служат различные элементы или их множества, например, яблоки и корзины яблок. С помощью порядкового счёта можно пронумеровать элементы и обозначить их общее количество.
Порядковый счёт связан со счётом группами, содержащими определённое равное количество элементов — например, счёт десятками яблок. Обычно это пальцы на двух руках (основание равно 10{\displaystyle 10}), но в исторических источниках встречаются группировки по 5,11,12,20,40,60,80{\displaystyle 5,11,12,20,40,60,80}. Количество элементов в группе служит основанием для системы счисления[11].
Числовой ряд, получаемый при счёте, называют натуральным, а его элементы — натуральными числами. Понятие натурального ряда впервые появилось в работах греческого математика Никомаха в I веке н. э., а натурального числа — у римского автора Боэция в конце V — начале VI века. Всеобщее употребление термина начинается с работ Д’Аламбера в XVIII веке. Архимед в своей работе «Псаммит» указал, что числовой ряд можно продолжать неограниченно, но вместе с тем заметил, что для реальных задач достаточно небольшого отрезка[13]. Деление натуральных чисел на чётные и нечётные приписывают пифагорейцам, оно также присутствует в египетском папирусе Ринда. Пифагорейцы также определили простые и составные числа[14].
Сложение, умножение, возведение в степень[править | править код]
 3+2=5{\displaystyle 3+2=5}
3+2=5{\displaystyle 3+2=5}Для натуральных чисел естественным образом определены операции сложения и умножения. При объединении двух наборов, содержащих некоторое количество предметов, новый набор будет иметь столько предметов, сколько было в первых двух наборах вместе. Если первый набор содержал 3{\displaystyle 3} предмета, а второй — 2{\displaystyle 2} предмета, то их сумма будет содержать 2+3=5{\displaystyle 2+3=5} предметов. Указанное действие носит название сложения и является простейшей бинарной операцией[4]. Для проверки корректности суммы таблицу сложения знать не обязательно, достаточно пересчитать предметы[15].
Многократное сложение элементов нескольких одинаковых множеств не зависит от порядка этих множеств, что позволило определить другую бинарную операцию — умножение[4]. Помимо умножения, в древности существовало отдельное арифметическое действие — удвоение, или умножение на два[16].
По аналогии с определением умножения через сложение, многократное умножение позволяет определить операцию возведения в степень.
Основные законы арифметики[править | править код]
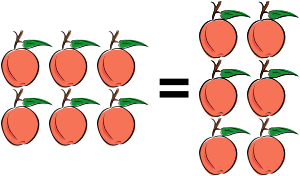 Переместительный закон умножения
Переместительный закон умноженияПро свойства этих операций сформулированы пять законов, которые считаются основными законами арифметики[17]:
- Коммутативность: переместительный закон сложения гласит, что от перемены мест слагаемых сумма не меняется. Аналогичный закон известен и для умножения, но он, конечно, говорит о множителях и произведении. Эти законы можно выразить в алгебраической форме с помощью буквенных обозначений:
- a+b=b+a{\displaystyle a+b=b+a}
- a⋅b=b⋅a{\displaystyle a\cdot b=b\cdot a}
- Ассоциативность: сочетательный закон сложения гласит, что складывая несколько слагаемых, можно группировать их в любом порядке. Аналогичный закон для умножения говорит о перемножении множителей. Эти законы также можно выразить в алгебраической форме:
- (a+b)+c=a+(b+c){\displaystyle (a+b)+c=a+(b+c)}
- (a⋅b)⋅c=a⋅(b⋅c){\displaystyle (a\cdot b)\cdot c=a\cdot (b\cdot c)}
- (a+b)⋅c=a⋅c+b⋅c{\displaystyle (a+b)\cdot c=a\cdot c+b\cdot c}
Помимо основных законов арифметики, для натуральных чисел выполняются также законы монотонности сложения и умножения[18][19], в алгебраической форме записываемые так:
- a+b>a+c{\displaystyle a+b>a+c} при b>c{\displaystyle b>c};
- a⋅b>a⋅c{\displaystyle a\cdot b>a\cdot c} при b>c{\displaystyle b>c} и a>0{\displaystyle a>0}.
Термин «коммутативный» для переместительного закона ввёл в 1814 году французский математик Сервуа. Термин «ассоциативный» для сочетательного закона ввёл в 1853 году Гамильтон[17].
Пуанкаре рассматривал все арифметические операции и законы с точки зрения интуиции. Утверждая, что законы очевидным образом выполняются для малых чисел, и используя правило индукции, можно прийти к выводу, что они выполняются для всех чисел. При другом подходе интуитивно выполнимыми считаются не все, а только простейшие законы, в то время как дальнейшее доказательство связано с логическими построениями[20]. Очевидными принимались переместительный и сочетательный законы[17]. Распределительный, или дистрибутивный закон в своих «Началах» доказывал ещё Евклид, используя геометрический метод[21].
Операция возведения в степень уже не коммутативна и не ассоциативна, у неё свои правила. Основные правила выполнения этой операции при положительных степенях очевидным образом следуют из её определения[4]. В алгебраической форме они могут быть записаны следующим образом:
- Дистрибутивность — распределительный закон для операции возведения в степень:
- an+m=anam{\displaystyle a^{n+m}=a^{n}a^{m}}
- он же, в случае вычитания, приобретает форму дроби:
- an−m=anam,n>m{\displaystyle a^{n-m}={a^{n} \over {a^{m}}},\quad n>m}
- Повторное возведение в степень раскрывается как перемножение степеней:
- (an)m=anm{\displaystyle \left(a^{n}\right)^{m}=a^{nm}}.
Обратные операции[править | править код]
У всех операций арифметики есть обратные: у сложения — вычитание, у умножения — деление, у возведения в степень — арифметический корень и логарифм. То, что у сложения и умножения по одной обратной операции, несмотря на их бинарность, объясняется их коммутативностью.
Вычитание: отрицательные числа[править | править код]
 5−2=3{\displaystyle 5-2=3}
5−2=3{\displaystyle 5-2=3}Вычитание — это операция, обратная сложению: разностью двух чисел 5{\displaystyle 5} и 2{\displaystyle 2} является x{\displaystyle x} из уравнения 2+x=5{\displaystyle 2+x=5}[4]. Обозначается операция вычитания знаком «−» и записывается в виде 5−2=3{\displaystyle 5-2=3}. Для выполнения операции применяли два приёма: отсчитывание от уменьшаемого числа единиц вычитаемого или подбор такого числа, прибавление которого к вычитаемому давало бы уменьшаемое[16].
Операция вычитания, если её применять ко всем парам натуральных чисел, а не только к таким, которые могли бы быть суммой и слагаемым в рамках операции сложения, позволяет выйти за пределы натурального ряда, то есть разность двух натуральных чисел не обязательно является натуральным числом — в результате вычитания может получиться ноль или вовсе отрицательное число. Отрицательные числа уже невозможно рассматривать как количество предметов, на числовой оси они расположены левее ноля. Множество чисел, получившееся добавлением к натуральным числам отрицательных чисел и числа ноль, носит название множества целых чисел. Ноль и множество натуральных чисел называются неотрицательные целые числа[4]. При умножении, чтобы определить, положительным или отрицательным будет произведение чисел, используют «правило знаков»[22].
Отрицательные числа считали ненастоящими и бессмысленными очень многие математики вплоть до XIX века, что, однако, не мешало их повсеместному формальному использованию. Впервые понятие отрицательных чисел появилось в Индии, где их толковали как «долг» (положительные числа — «имущество»). Распространение же отрицательные числа получили только в XVII веке[23]. Термин «вычитание» появился ещё у Боэция, термины «вычитаемое» и «уменьшаемое» ввёл в обиход Вольф в 1716 году, «разность» — Видман в 1489 году[16]. Современное обозначение знаками «+» и «−» было также введено Видманом в конце XV века.
Деление: рациональные числа[править | править код]
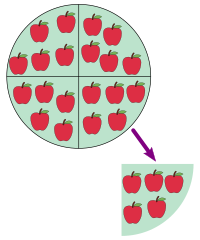
Обратной к операции умножения является операция деления. Первое определение деления — это поиск числа, которое содержится в делимом столько раз, сколько единиц содержится в делителе. Такое определение дано в учебниках арифметики XIV века — например, 20:4=5{\displaystyle 20:4=5}. Деление считалось очень сложной и громоздкой операцией. Современный способ деления, использующий частичные произведения делителя на отдельные разряды частного (деление столбиком), представлен в итальянском манускрипте 1460 года[16].
Для натуральных чисел, не являющихся множителем и произведением, известна операция деление с остатком (а определение собственно остатка от деления также называется деление по модулю). Также существует множество способов, упрощающих деление в различных частных случаях или позволяющих проверить делимость на то или иное число. Например:
- число без остатка делится на два, если его последняя цифра при десятичной записи делится на два;
- число без остатка делится на три, если сумма всех его цифр при десятичной записи делится на три;
- число без остатка делится на десять, если его последняя цифра при десятичной записи — ноль.
Операция деления, если делить не только те числа, которые можно получить умножением натуральных чисел, и при этом не выделять остаток, так же как и вычитание, позволяет выйти за пределы множества натуральных чисел. При делении могут получиться дроби, которые невозможно без остатка сократить до целого. Числа, соответствующие таким дробям, называются рациональными. За счёт осознания основанных на делении рациональных чисел происходит ещё одно расширение перечня известных видов чисел. Исторически сначала появилось понятие дроби, а затем отрицательного числа[24]. Такой же порядок принят в школьном курсе[25].
Используется две формы записи дробей — в виде числителя и знаменателя, разделённых горизонтальной или наклонной чертой и часто сокращаемых до минимальных чисел, и в виде цифр дробной части, размещаемых после знака-разделителя целой и дробной части в позиционной записи числа. Например, результат деления 10 на 20 может быть записан как 1020=10/20=5/10=1/2=0,5{\displaystyle {\frac {10}{20}}=10/20=5/10=1/2=0{,}5}.
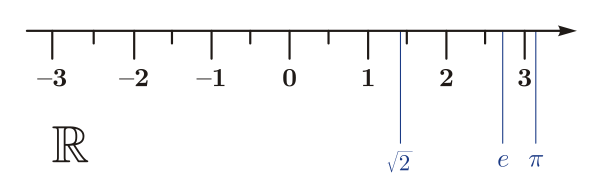
Извлечение корня: иррациональные и комплексные числа[править | править код]
Одна из двух обратных для возведения в степень операций — извлечение корня, или поиск числа, которое при возведении в соответствующую степень будет давать известный результат. То есть, говоря алгебраически, это поиск корня для уравнения вида xa=b{\displaystyle x^{a}=b}. Вторая обратная операция — поиск логарифма (корня для уравнения вида ax=b{\displaystyle a^{x}=b}). К арифметике, как правило, относят лишь вычисление корня второй степени — квадратного корня.
Операция вычисления корня, если выполнять её не только для тех чисел, которые можно получить возведением в степень натуральных чисел, так же как и остальные обратные операции, позволяет выйти за пределы множества натуральных чисел. Числа, которые получаются при этом, часто не могут быть представлены в виде конечных рациональных дробей и поэтому названы иррациональными. Множество чисел, полученное добавлением к рациональным числам иррациональных, назвали вещественными или действительными.
Ещё в Древней Греции было известно о существовании несоизмеримых отрезков, как минимум, на примере сторон и диагонали квадрата со стороной, принятой за единицу, и проводились попытки получить для них точные числовые значения, что нашло отражение в «Началах» Евклида. Вещественные числа стали объектом исследований только в XVII—XVIII веках. Во второй половине XIX века Дедекинд, Кантор и Вейерштрасс сформулировали свои конструктивные способы определения вещественного числа[26].
Для операции извлечение корня известно следующее правило[4]:
- anm=anm{\displaystyle a^{n \over m}={\sqrt[{m}]{a^{n}}}}.
Дальнейшее расширение множества чисел было связано с невозможностью извлечения квадратного корня из отрицательного числа. С подобной задачей сталкивались в древности при решении квадратных уравнений, и такие уравнения просто считали неразрешимыми. В первой половине XVI века стали выражать решения таких уравнений через корни из отрицательных чисел и называть такие корни «мнимыми», «невозможными», «воображаемыми» и т. д.[27]
Практическая сторона арифметики включает в себя методы, схемы и алгоритмы для осуществления точных арифметических действий, в том числе использование счётных машин и других устройств, а также различные приёмы приближённых вычислений, которые появились в связи с невозможностью получить точный результат при некоторых измерениях и позволяют определить его порядок, то есть первые значащие цифры[28].
Точные методы[править | править код]
Начиная с XV века предлагались разные алгоритмы для осуществления арифметических операций над многозначными числами, которые отличаются характером записи промежуточных вычислений[1]. Арифметические алгоритмы построены на действующей позиционной системе счисления, когда любое положительное действительное число x{\displaystyle x} единственным образом представимо в виде
- x=(an−1an−2…a1a0,a−1a−2…)b=∑k=−∞n−1akbk{\displaystyle x=(a_{n-1}a_{n-2}\dots a_{1}a_{0},a_{-1}a_{-2}\dots )_{b}=\sum _{k=-\infty }^{n-1}a_{k}b^{k}}, где a{\displaystyle a} — очередная цифра записи числа x{\displaystyle x}, b{\displaystyle b} — основание системы счисления, n{\displaystyle n} — число разрядов целой части числа x{\displaystyle x}.
Все действия над числами используют таблицы сложения и умножения до десяти и основные арифметические законы. В качестве иллюстрации известный популяризатор науки Клейн приводит следующий пример:
- 7⋅12=7⋅(10+2)=70+14=70+(10+4)=(70+10)+4=80+4=84,{\displaystyle 7\cdot 12=7\cdot (10+2)=70+14=70+(10+4)=(70+10)+4=80+4=84,}
в котором используются распределительный и сочетательный законы[29].
Потребность в быстрых и точных вычислениях привела к созданию простейших счётных устройств: абака, суаньпаня, юпаны или счёт. Следующим шагом было создание Отредом в 1622 году логарифмической линейки, которая позволяет производить умножение и деление[30].
Компьютерная арифметика[править | править код]
 Копия вычислительной машины Шиккарда
Копия вычислительной машины ШиккардаКнут считал арифметические действия «уделом компьютеров»[31]. Первые вычислительные машины, которые позволяли механизировать четыре арифметических действия, были сконструированы в XVII веке. «Арифметическая машина» Шиккарда, как он сам её называл, была построена в 1623 году. Операции сложения и вычитания производились посредством вращения цилиндров, специальные цилиндры были также для умножения и деления. Кроме того, машина могла переносить десятки. Машина Паскаля была разработана им в 1642 году для помощи отцу в выполнении финансовых расчётов. Она имела тот же принцип действия, что и машина Шиккарда. Основную часть машины составлял механизм переноса десятков. Вместе с тем, ремесленное изготовление таких машин всё ещё оставалось невыгодным[32]. Попытки усовершенствовать арифмометр продолжались весь XVIII век, но только в XIX веке применение арифмометров получило широкое распространение[33].
В XX веке на смену арифмометрам пришли электронные вычислительные машины. В их основе лежат алгоритмы, которые используют наименьшее число элементарных операций для выполнения арифметических действий[1]. Компьютерная арифметика включает алгоритмы выполнения операций над числами с плавающей запятой, дробями и очень большими числами[31].
Измерение[править | править код]
Помимо предметов, которые подлежат пересчёту, существуют предметы, которые можно измерить — в первую очередь, это длина и масса[34].
Как и при счёте, первыми мерами длины у человека были пальцы рук. Затем расстояние стали мерить шагами, двойными шагами, милями (тысяча двойных шагов), стадиями. Кроме того, для измерения длины использовали локти, ладони, сажени, дюймы. В различных регионах устанавливались свои системы мер, которые редко были кратны десяти[35]. Многообразие мер, в частности, позволяло обойтись без использования дробей[36][37]. Торговая арифметика включала в себя умение оперировать величинами (денежными единицами, единицами мер и весов) в недесятичной системе счисления[38].
В конце XVIII века французским революционным правительством на основании временного, а затем и архивного (законом 10 декабря 1799 года) метра была принята метрическая система мер (окончательно Франция перешла на неё с 1 января 1840 года). Вместе с метром был определён и килограмм. В основе метрической системы лежит десятичная система. Именно это обстоятельство позволило ей распространиться почти на весь мир (исключение составляют
