УСТНЫЙ СЧЕТ ПО-ЯПОНСКИ — Головоломки для поднятия настроения — православная социальная сеть «Елицы»
Как японцам удается считать в уме быстрее, чем на калькуляторе? Об этом данная выдержка из научно-популярной книги.
Абак был изобретен как способ простого счета, но по-настоящему сила этого инструмента проявилась, как только его стали использовать в качестве средства для вычислений. Арифметика значительно упростилась, когда в дело оказались вовлечены передвигаемые по стержням бусинки. Например, чтобы вычислить сумму «3 плюс 1», мы начинаем с того, что передвигаем 3 бусинки, затем передвигаем одну бусинку — и ответ готов — 4 бусинки прямо у вас перед глазами. Чтобы вычислить, скажем, сумму «31 плюс 45», в двух соседних колонках сдвигаем 3 бусинки и 1 бусинку, а затем перемещаем к ним 4 бусинки и 5 бусинок соответственно. Получаем 7 бусинок в левой колонке и 6 бусинок в правой, это и есть ответ: 76. После небольшой тренировки сложение чисел любой длины не представляет никакой трудности, нужно только иметь достаточно колонок, в которых эти числа могли бы разместиться. Если на какой-либо колонке сложение двух чисел дает в результате число больше десяти, надо передвинуть бусинки в соседней слева колонке. Например, 9 плюс 2 дает 1 бусинку в левой колонке и 1 бусинку в исходной колонке, что и представляет собой ответ: 11. Вычитание, умножение и деление выполняются немного более хитрым способом, но коль скоро вы их освоили, вычисления совершаются на удивление быстро.
Владение абаком в Японии по-прежнему считается чрезвычайно важным для подрастающего поколения; вычисления на этом устройстве остаются одним из основных внеклассных занятий наряду с плаванием, игрой на скрипке или дзюдо, причем обучение работе на абаке ведется в духе обучения боевым искусствам. Уровни мастерства измеряются в данах, проводятся соревнования разного уровня и даже чемпионаты страны. Как-то воскресным днем я отправился на такой региональный турнир. В нем участвовали без малого триста детей от 5 до 12 лет. Они сидели за партами в конференц-зале, вооруженные целым набором «соробанных» аксессуаров типа модных футляров для них. Перед первой партой стоял диктор. С интонацией нетерпеливого муэдзина он оглашал числа, которые предстояло складывать, вычитать или умножать. Соревнование шло на выбывание и продолжалось несколько часов. Когда пришло время вручать победителям награды — каждая из которых включала крылатую фигуру, в поднятых руках держащую абак, — из динамиков зазвучала музыка в исполнении военного духового оркестра.
После нескольких лет обучения работе на абаке вы настолько хорошо усваиваете расположение бусинок, что можете выполнять вычисления, просто мысленно представляя его себе. Эта процедура, называемая «анзан», выглядит довольно занятно — несмотря на то, что и смотреть-то, вообще говоря, не на что! Я наблюдал, как это происходит, в клубе любителей абака в Токио. Преподаватель Юдзи Миямото читал числа, обращаясь к замершей и погруженной в полную тишину аудитории, после чего в течение нескольких секунд ученики поднимали руки, показывая, что ответ готов. Один ученик по имени Наоки Фуруяма сказал мне, что он может мысленно представить себе абак с восемью столбцами. Другими словами, его воображаемый абак позволяет изображать все числа от 0 до 99 999 999.
Клуб любителей абака, которым руководит Миямото, — один из самых известных в стране: его ученики получают немало данов за разнообразные достижения во время чемпионатов страны, однако специализируются в этом клубе именно на анзане. Несколько лет назад Миямото решил придумать такой тип арифметических задач, которые решаются только на анзане. Например, когда вы задаете ученикам какой-то пример, ответ можно получить различными способами: используя калькулятор, карандаш и бумагу, или же абак, или анзан. Миямото хотел продемонстрировать, что имеются ситуации, когда анзан представляет собой единственный возможный метод.
164, 597, 320, 872, 913, 450, 568, 370, 619, 482, 749, 123, 310, 809, 561.
Каждое число возникало только на 0, 2 секунды, так что вся процедура уложилась в три секунды. Задача состояла в том, чтобы определить сумму всех чисел. Они мелькали так быстро, что я едва их уловил. И тем не менее вскоре после того, как промелькнуло последнее, улыбающийся Наоки Фуруяма выдал ответ: сумма чисел равна 7907.
Задачу для «Мелькающего анзана» невозможно решить с помощью калькулятора или абака, потому что нет времени даже на то, чтобы запомнить числа, промелькнувшие перед вами, не говоря уже о том, чтобы набрать их на клавиатуре или передвинуть руками бусинки. Анзан не требует запоминания чисел. Все, что нужно, — это лишь мысленно передвигать бусинки каждый раз, как на экране возникает новое число. Увидев число 164, вы немедленно представляете себе абак, на котором выставлено 164. Когда вы видите число 597, ваш внутренний абак перестраивается в соответствии с получающейся суммой, которая равна 761. Выполнив 14 сложений, вы не в состоянии вспомнить ни промелькнувшие числа, ни промежуточные суммы, но воображаемый абак у вас в голове тем не менее показывает ответ: 7907.
«Мелькающий анзан» немедленно завоевал популярность по всей стране, а компания «Nintendo» даже выпустила игру «Мелькающий анзан» для своей DS-консоли. Миямото показал мне отрывки из телевизионной игры «Мелькающий анзан», в которой подростки — виртуозы анзана сражались под восторженные крики болельщиков. Миямото считает, что эта игра способствовала привлечению большого числа учеников в абак-клубы по всей Японии. «Люди и не подозревали, на что они, оказывается, способны при хорошем владении соробаном, — говорит он. — Зато теперь, когда эти передачи стали показывать по телевидению, они это осознали».
Из книги: Алекс Беллос. «АЛЕКС В СТРАНЕ ЧИСЕЛ. Необычайное путешествие в волшебный мир математики»
японские счеты. Или завидуйте молча: mil_yume — LiveJournal
В комментариях к моему посту про скрытые функции калькулятора многие возмутились, что, мол, 21 век на дворе, эксель им на что! И вообще, еще б на счетах вообще считали! Ну, пост вышел в топ, поэтому я не удивлена комментариями. Даже забавно: пост про калькулятор, а комментарии про тупость японцев. Ну-ну. Чем еще оправдать собственное незнание? 🙂Как бы там ни было, сегодня я не об этом. Просто смешки про счеты навели меня на воспоминание об одном фильме, который я тут посмотрела. Это был скомпилированный документальный фильм о проникновении бытовых электроприборов в жизнь простой японской семьи.Речь шла о второй половине 20 века, и на истории одной простой семьи показали, различные исторические события. Как появился первый пылесос, первый телевизор, первые многоквартирные дома. И все это на одной семье: вот, мама метет татами с клочками мокрой газеты (Кстати, асфальта тогда еще мало было, так что пыль скапливалась чуть ли за день-два. Так что мести приходилось часто), а тут папа принес первый пылесос. Какой он был? Как к нему отнеслись? Так же про телевизор, тостер, переезд в квартиру, первый супермаркет, первая пачка кубиков карри и т.п.
И был там интересный момент про школьника — сын, типа, их. Он делал домашнее задание со счетами, так как калькуляторов еще не было. А на счетах — наклейки. Старшее японское поколение, наверное, сразу догадалось, что это, а младшему показали кусочек документальной съемки с экзамена по счетам. Экзамен по счетам! Тем, кто сдал, выдавалась наклейка с определенным уровнем. Причем экзамен, сказали, считался очень важным: школьникам, сдавшим первый уровень, пророчили карьеру банкира 🙂
そろばん2級
Очень интересная передача была, я такие люблю. Но вот найти ее не получилось. Может, у вас получится?
В общем, потом появился калькулятор, и счеты исчезли из нашей жизни. Ну, так я думала, пока искала видео с каким-нибудь хотя бы отрывком того фильма. Но нашла кое-что получше.
Оказывается, экзамен по счетам проводится до сих пор! Более того, японские первоклашки учат счет по счетам. Говорят, так понятнее, чем считать на бумаге или в уме. Хотя думаю, что такие занятия скорее дополнительные…
アビリードそろばんスクール
Я даже нашла видео с всеяпонского экзамена в хорошем качестве! Вы только посмотрите — там чудеса!
Мало того, что дети очень быстро считают, вы только ведущего послушайте! Я не могу разобрать ни одного слова, хотя там только числа по сути XD Победившая девочка тоже великолепна. Хоть сейчас в аниме ее 🙂
Вернусь к главному, что я хотела сегодня сказать.
Японцы не только умеют использовать калькулятор на все 100%, но и на счетах со скоростью света считают. Бгг, кто-то все еще сомневается, что они эксель не знают?
ПОДПИСАТЬСЯ
Счёты Абакус. Ментальная арифметика.
Счёты Абакус. Ментальная арифметика.
Куликова А.Р. 11МБОУ «Смоленская СОШ №2»
Левашова Л.А. 11МБОУ «Смоленская СОШ №2»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Методика счета под названием Соробан сегодня распространяется со скоростью света. Ее цель – развить умственные способности детей, равномерно задействуя левое и правое полушария. Этой методике более 25 лет в Японии, 3 года она работает в постсоветских странах. Но самое интересное, что счетам, на основе которых она построена, уже более 2,5 тысяч лет. И только сейчас из далеких стран Азии этот инструмент счета начинает распространяться по всему миру.
Мы решили познакомиться с данной методикой более подробно.
Цель работы: научиться считать на счётах абакус, развить навыки устного счёта.
Гипотеза: счёты абакус и ментальная арифметика способны развить умственные способности настолько, что любые арифметические задачи станут решаться простым и быстрым вычислением в уме.
Для подтверждения выдвинутой гипотезы были поставлены следующие задачи исследования:
-изучить научную литературу по теме исследования.
-изготовить счёты абакус и научиться ими пользоваться.
-Обобщить результаты работы.
Объект исследования ментальная арифметика.
Предмет исследования: счёты абакус.
Методы работы: поисковый метод с использованием научной и учебной литературы, а также поиск необходимой информации в сети Интернет; анализ полученных в ходе исследования данных.
Счёты Абакус
Абакус (Абак), или Соробан – это древние счеты, которые использовали в древних странахАзии и Европе. В Китае они назывались абак (по-латыни «абакус»), в Японии – Соробан. Однако применяли их также в Древнем Риме и Греции. Абакус несколько видоизменялись в зависимости от страны, где они использовались, но суть оставалась прежней.
Счеты представляют собой рамку, разделенную перекладиной. В верхней части расположена одна линия косточек. Каждая косточка в ней означает «пять». Внизу расположены ряды косточек, в каждом из которых по 4 косточки. Каждая из них обозначает «один». Косточки на счетах Соробан, или Абакус специально заострены, чтобы дети, перебирая их, развивали мелкую моторику. Счеты Абакус обозначают единицы, десятки, сотни, тысячи и миллионы. С помощью Соробан дети быстро осваивают устный счет и даже могут перемножить многозначные числа.
Есть магазины в Китае, где торговцы до сих пор используют счеты для подсчета.
На фотографии ниже, Эд Бирн в 2013 году в магазине в Гонконге.
Счеты до сих пор используют торговцы в Азии и «Чайна-тауны» в Северной Америке. Абакус до сих пор учат в азиатской школе, и несколько школ на Западе. Слепых детей учат использовать абак там, где их зрячие коллеги будут использовать бумагу и карандаш для выполнения расчетов.
«В частности, мы пользуемся счетами при обучении детей математике, и особенно умножению; счеты-это отличная замена для заучивания наизусть таблицы умножения. Абак-это также отличный инструмент для обучения другим базовым системам нумерации, поскольку она легко приспосабливается к любой базе.
Ментальная арифметика
Как проходят занятия? Методика обучения на счетах Соробан, или Ментальная арифметика, позволяет развить способности детей до небывалых высот. Основным инструментом при этом являются счеты Абакус. На первом этапе дети учатся пользоваться счетами. На втором этапе дети представляют счеты Соробан в уме. Т.е. ребенок начинает представлять Соробан перед собой и производить вычисления в уме. При этом осваиваются 3 математические действия: сложение; вычитание; умножение; Обучение продолжается 2 года. Лучше всего начинать обучение в возрасте ребенка от 5 до 11 лет. Этот возраст считается оптимальным. Но это не означает, что методика Соробан недоступна для старших детей и взрослых, просто для обучения может потребоваться больше времени. Занятия в центрах Соробан проходят в течение 2 часов 1 раз в неделю. На дом детям даются задания. Если они выполнены, тренер открывает доступ к следующим. Для выполнения задания достаточно четверти часа в сутки. Программа может корректироваться индивидуально в зависимости от того, как успевает каждый ребенок.
Как пользоваться? Чтобы научиться пользоваться счетами, необходимо знать, что они из себя представляют.
Счеты состоят из: рамки; разделительной полосы; верхних косточек; нижних косточек. Посередине находится центральная точка. Верхние косточки обозначают пятерки, а нижние – единицы. Каждая вертикальная полоса косточек, начиная справа налево, обозначает один из разрядов цифр: единицы; десятки; сотни; тысячи; десятки тысяч и т. д. Чтобы отложить число, необходимо на счетах придвинуть к разделительной линии косточки, по числовому обозначению соответствующие цифре каждого разряда. Например, чтобы отложить число 165, необходимо на первой линии справа придвинуть верхнюю косточку (она обозначает пятерку), на второй линии – верхнюю и одну нижнюю косточку (5+1=6), на третьей линии – одну нижнюю. Так мы получаем требуемое число. Дальнейшие вычисления будут сопровождаться передвижением косточек по линиям соответственно разрядам.
Правила работы на соробане
Прежде чем начинать заниматься непосредственно вычислениями, новичку необходимо овладеть простейшими навыками работы на соробане. Они заключаются в следующем:
1). Откладывать числа от 1 до 9 по порядку;
2). Откладывать числа от1 до 9 в различной последовательности;
3). Отрабатывание сброса;
При этом не следует забывать, что на соробане работают всегда СЛЕВА НАПРАВО большим и указательным пальцами обеих рук.
Сброс производится посредством резкого наклона счет, затем провести указательным пальцем вдоль перегородки, отбивая косточки верхнего отделения вверх.
Данный тренинг следует проводить ежедневно, чтобы не терять обретенных навыков. После того, как обучающийся овладел данным упражнением, стоит потренироваться в зрительной оценке чисел, выложенных на счетах, для того чтобы быстро определять число, а не заниматься его подсчитыванием. Именно с этой проблемой сталкивается большинство учеников, поэтому этот навык необходимо отработать и уделить ему особенно пристальное внимание.
Сложение
После необходимой всем начинающим тренировки беглости пальцев можно приступать к выполнению одного из простейших вычислений – сложению. У него есть только один способ. Для того чтобы нагляднее его представить, начнем с простого примера.
Отложим на счетах число 21.
Возьмем ряд G и соседний с ним. Понятно, что число 2 откладывается на ряду G, а 1 на Н, так как числа откладываются слева направо, начиная с большего разряда. Впредь число 21 – число отсчета или базовое число. (Стоит заметить, почему были выбраны именно эти ряды. Дело в том, что их расположение цифр на них сходно с положением цифр на обычном электронном калькуляторе, поэтому не стоит усложнять задачу.)
А теперь прибавим к базовому числу 6.
Мы видим, что эта задача решена, если отложить на счетах всего две косточки – на верхнем ряду косточка опускается вниз (что означает прибавление к числу 21 пяти) и откладыванием вверх еще одной косточки (в сумме с они образуют 6). Не стоит забывать что все эти преобразования происходят в ряду Н, так как он является рядом меньшего разряда.
Путем зрительной памяти не сложно определить, что получается при выполнении сложения – суммой 21 и 6 является число27.
Продолжим суммирование. Для примера нередкой ситуации «вычитания в сложении» прибавим к полученному числу 27 (теперь оно – базисное) 15. Для этого в ряд G добавляем одну косточку, которая символизирует «1» в 15.
Осталось лишь прибавить «5» из числа 15. Но так как в ряду Н уже существует 7, то необходимо поступить следующим образом: косточку в верхнем отделении поднимают,»отнимают 5″, но тут же прибавляют косточку в нижнем отделе следующего разряда»прибавляют 10″ в ряду G. Это ключевой момент в сложении на соробане, когда косточек для сложения на данной линейке не хватает – прибавляют одну косточку к старшему разряду (внизу) и отнимают необходимое количество на данной линейке. Сначала надо делать движения на младшей линейке (H), затем на старшей(G)
Видно, что получается число 42, которое и будет являться суммой чисел 27 и 15.
В качестве подобного примера, для закрепления ситуации «вычитания в сложении», возьмем следующий несложный пример.
Отложим на счетах число 14 (работа начинается, прежде всего, со сброса предыдущего примера; она продолжается в тех же рядах – Н и G).
Работая слева направо, откладываем одну косточку на ряду G, и четыре – на ряду Н. На первый взгляд прибавление к 14 единицы не составит труда. Однако выполнение этой задачи на соробане требует логического мышления и тренировки. Итак, для того чтобы решить пример 14+1 следует работать с рядом Н (ведь именно он — меньший разряд), причем отложив косточку в верхнем ряду, а четыре косточки в нижнем ряду сбрасываются.
Мы можем видеть результат: 14+1=15
Отлично, теперь решим задачу потруднее. Не несколько цифр, а общие действия слева направо в многозначном числе. Давайте попробуем 3345+6789 (=10134)
Для начала отложим 3345 в окне соробана:
Следующим шагом, мы должны «прибавить 6» из 6789 на линейке Е.
Получили число 9345 , это не окончательный ответ, мы должны прибавить еще три числа! Следующий шаг «прибавить 7» на линейке F. здесь как раз тот случай, когда надо подумать. Представим себе, что мы «Прибавим 10 и отнимем 3» это тоже самое, что «прибавим 7». Мы должны передвинуть три косточки вниз на линейке F (отнять 3), а затем передвинуть вверх 1 косточку (прибавить 10 ) на линейке Е. Но там нет возможности добавить косточку, поэтому добавляем ее на следующей линейке слева, а переполненную линейку сбрасываем. Это и есть ключевая концепция соробана.
Это число 10045. Но это не все. Еще есть два числа. Как вы видите, осталось повторить процесс сложения – и на практике это получается довольно просто. Следующим шагом мы должны «прибавить 8» на линейке G. Снова не хватает косточек. И здесь мы должны «Отнять 2, прибавить 10». Следовательно, мы должны опустить две косточки на G и поднять одну косточку на линейке F.
Результирующее окно перед вами:
Теперь имеем число10125. Скоро конец! Берем для сложения последнюю цифру «9». Мы должны добавить 9 на линейке H. Опять не хватает косточек и мы должны по старой схеме «прибавить 10, отнять 1» Для вычитания 1 на линейке Н мы должны «Отнять 5» и «прибавить 4». Не забудем теперь, что мы должны еще прибавить 1 на линейке G. После выполнения этого шага теперь получаем следующую картину:
Видно, что это число 10134, что является суммой чисел 3345+6789
Много проще и аккуратнее, чем вы бы делали это на бумаге
Вычитание
Вычитание на соробане такое же простое как и сложение, это обратный процесс. Вместо переносов на десятки (следующая линейка слева), теперь прийдется занимать с этой же самой линейки. В целом для вычитания стиль работы с примерами и числами слева направо — по одной линейке. Если на текущей линейке у вас не хватает косточек для вычитания нужного числа – вы должны отнять «1» от старшего разряда (слева) а на текущий добавить разницу. Мы хотим дать конкретный пример для демонстрации простоты процесса.
Возьмем число 47:
И вычтем из него 21. Начинаем с линейки G и «вычитаем 2» простым перемещением 2 косточек вниз.
Теперь мы имеем значение 27 (но это еще не конец)
Теперь переходим к единичной линейке и «Отнимаем 1» перемещением одной нижней косточки вниз. Здесь имеем конечный ответ 26.
Теперь отнимем 4 из этого. Мы должны перейти на единичную линейку и «Отнять 4», но так как в нижней ее части не хватает косточек для такого вычитания, заменяем действия на «Отнять 5, прибавить 1». Для выполнения этого отодвигаем верхнюю косточку от перегородки, а снизу добавляем одну. Имеем ответ 22. (Это результат вычитания 26-4):
Теперь продемонстрируем способ «заёма». Возьмем 22 на соробане и отнимем 14. Сначала отнимем 1 на линейке G, это просто. Наш результат (не конечный) будет:
Теперь мы должны «Отнять 4″ на единичной линейке H. Так как мы не имеем достаточно косточек, мы должны заменить действие на » Отнять 10, прибавить 6″ для получения того же результата. Отодвинем одну нижнюю косточку на линейке G (надо помнить, что каждая косточка на линейке слева «весит» 10 единиц относительно той линейки, что справа) и «прибавим 6» на линейке H. Для этого придвинем к перегородке одну косточку сверху, одну снизу(5+1=6). Результат на соробане 8 – это и есть ответ!
УМНОЖЕНИЕ
Умножение есть не что иное как многократное сложение. Но вместо того, что бы 23 раза прибавлять одно и тоже число, легче выполнить его умножение. Существует особая техника выполнения умножения в окне соробана. Есть несколько различных методов. Здесь приводится метод, который был рекомендован Японским Комитетом по Абакусу. Этот метод считается дающим меньше ошибок и простым в обучении.
Теперь поставим перед собой задачу умножения 23Х47. Число 23 будет называться множимым, а число 47 – множителем. Прежде всего расположим множимое (а это число 23) вблизи центра счетной доски. Пропустив пустую линейку, число 47 (множитель) расположим слева
Между числами пропущены линейки для лучшей наглядности, при не таких маленьких счетах можно пропускать и больше.
Процесс умножения подобен тому, как мы делаем это на бумаге, но отличается последовательностью выполнения действий
Сначала берем правую цифру множимого ( 3) и умножаем на крайнюю левую цифру множимого 3х4=12. Число 12 откладываем слева от множимого (на линейках FG)
затем эту же цифру множимого умножаем на следующую слева направо цифру множителя 3х7=21, получившееся число 21 прибавляем к результату, но уже сдвинув вправо на один разряд (линейки GH ) :
Теперь мы не нуждаемся в цифре 3, так как с ней уже все проделано, очистим эту линейку (E ) для дальнейшей работы
Теперь берем следующее число множимого – в нашем случае это 2. Умножаем его на левую крайнюю цифру множителя. Результат (2х4=08) прибавляем к линейкам EF. Поскольку в общем случае результат занимает 2 разряда, одноразрядный результат надо представлять в виде 08, что бы правильно разместить его на линейках, так получается следующая картина:
В заключение мы должны умножить 2 на оставшуюся цифру множителя 7 и получившийся результат 14 прибавить на линейки FG
К линейке F надо прибавить 1, но она полностью заполнена, поэтому по правилам сложения, прибавляется 1 к следующему разряду (E), а здесь отнимается 9. Затем к линейке G прибавляется 4
Деление ( В сотрудничестве с Тоттон Хеффельфингером)
Приступая к делению можно испугаться его сложности. Но надо всего лишь знать таблицу умножения и помнить, что деление – это не более чем многократное вычитание
Здесь использована техника, описанная в книге «Японский Абакус — использование и теория» Такаши Койима
В описании метода я использовал стандартную терминологию. Например, в задаче 8/2=4, 8 является делимым, 2 является делителем, а 4 является частным
Для решения задач на деление делимое на соробане размещается чуть правее центра, а делитель левее. Обычно делимое и делитель разделены тремя-четырьмя свободными линейками, и здесь формируется частное. Надо сказать, что иногда четырех линеек не хватает и приходится использовать больше. Это зависит от задачи.
Пример. 837 ÷ 3 = ?
Шаг 1: Расположите делимое 837 на правой стороне абакуса ( в нашем случае на линейках G, H,I) и делитель 3 слева (на линейке B) предусмотрите, что бы цифра 7 попала на единичный разряд ( с меткой)
|
Имеем результирующее окно: |
|
Step 1 A B C D E F G H I J K L M |
Шаг 2: Т. к. для расположения частного достаточно трех разрядов, первую его цифру расположим на линейке D, тогда единицы придутся на линейку F. Порядок деления числа 837 на 3 начинается с деления 8 на 3 это будет 2 с остатком. Расположим число 2 на линейке D. Умножаем 2 х 3 получаем 6, затем отнимаем 6 от 8 получаем в остатке 2
|
Это результирующее окно: |
|
Step 2 A B C D E F G H I J K L M
2 — 6 |
Шаг 3: Новое значение 237 расположено на линейках GHI. Продолжим деление 23 на 3. Число 3 содержится в 23 7 раз с остатком. Расположим 7 на линейке Е. Произведение 7х3 равно 21, вычтем 21 из 23 получим остаток 2.
|
Имеем результирующее окно |
|
Step 3 A B C D E F G H I J K L M
7 — 2 1 |
Шаг 4 и результат: Теперь имеем число 27 слева на линейках H I. Продолжим деление на 3 числа 27. 3 содержится в 27 девять раз. Размещаем 9 на линейке F. Умножаем 9х3=27, затем отнимаем 27 от 27 получаем 0. Предусмотрите что бы цифра 9 попала на единичную линейку F
|
Мы имеем 279 – это правильный результат |
|
Step 4 A B C D E F G H I J K L M
9 — 2 7 |
Заключение.
Что дает ментальная арифметика? Японские счеты под названием Соробан учат не только считать, хотя в этом дети добиваются небывалых успехов. Малыши с легкостью вычисляют в уме 10-значные числа, умножают и вычитают. Но быстрый устный счет не главная цель. Считать – лишь способ развивать умственные способности. Ментальная арифметика способствует: умению концентрироваться; активизации слуховой и зрительной памяти; совершенствованию интуиции и смекалки; умению нестандартно решать проблемы; проявлению самостоятельности и уверенности в себе; реализации способностей и успешной карьере в будущем. В основе методики лежит сила воображения. Именно благодаря ей удается ускорить мышление, наладить ускоренные связи между правым и левым полушариями мозга. Дети, которые учились по методике Соробан, быстрее осваивают иностранные языки, хорошо учатся в школе, более целеустремленные.
Действительно ли метод обучения столь эффективен? Отзывы в основном положительные: дети уже через пару месяцев начинают быстро считать и лучше соображать. В основном родители довольны: дети подтягиваются по предметам, становятся внимательнее и сосредоточеннее. Но у некоторых ребят случаются неудачи. В основном это связано с тем, что задания в школе Соробан следует выполнять ежедневно. Некоторых детей трудно усадить ежедневно за выполнение заданий, и они не успевают усваивать курс. Таким образом, родители должны внимательно следить за реакцией ребенка на обучение. Если ему нравится, он успевает, и занятия не становятся предметом для слез и переживаний, можно продолжать.
Список использованной литературы иных источников:
http://pandia.ru/text/77/413/58255.php
https://yandex.ru/images/
http://fb.ru/article/247553/chto-takoe-mentalnaya-arifmetika
http://steshka.ru/kak-schitat-na-abakuse-sorobane
https://www.youtube.com/watch
Просмотров работы: 300
Умножение по-японски
В японских школах уроки математики сильно разнятся с теми, к которым мы привыкли в России. Есть в их школах нечто такое, что завораживает, заставляет удивиться и произнести:” Такое возможно?”. Интересно, почему так? С этим нам и придется разобраться.
Менталитет Японии сильно разнится с нашим. Поэтому многое, что присуще японской системе образования, нами было бы вряд ли принято и понято. Но все же у них есть, чему поучиться.
Естественно, что так же как и у нас, японские школьники учат таблицу умножения во втором-третьем классе. У нас этот процесс чаще похож на скучное заучивание цифр и их произведение. Помню свой то ли второй, то ли третий класс: нам дали задание выучить таблицу на каникулах, моя бабушка сходила на рынок, купила большой плакат с таблицей и каждые два часа заставляла меня повторять. Под таким напором и весь курс математики за неделю можно выучить. Но такой способ не очень приятный, да и не всегда рабочий.
В Японии дети учат особую рифмованную таблицу, которая имеет специфическое название — «kuku».Необычность этой системы заключается в запоминании таблицы на скорость. Там даже есть целые турниры со скоростным решением примеров и задач! Сначала дети практикуются в своем классе, потом перед всей школой. Слышали об олимпиадах в США, где дети в актовом зале должны быстро разобрать слова на буквы и звуки? Что-то такое есть в Японии, только с таблицей умножения.
Такая система эффективна благодаря своей соревновательной идеи. Ребенок чувствует азарт, хочет проявить себя и стремится быть лучшим среди своих одноклассников. Ведь каждому из нас нравится стремиться к победе!
Хотели бы иметь на стенке сертификат о лучшем знании таблицы умножения среди учеников 2 класса? Я бы хотел. 🙂
В Японии к ментальной арифметике относятся с любовью. Дети в полной мере развивают счет в уме с младших классов, но только после того, как научатся считать на специальной доске — абаке , собране или абакусе. Нашим языком — счеты. Наверное, у каждого из нас была эта доска дома, которой никто не пользовался с момента появления калькуляторов. И, кажется, я так и не научился ей тогда пользоваться.
Есть еще интереснее метод умножения в Японии, который даже в первом классе объясняют. Забавно, но в нем заучивание вовсе не требуется! Достаточно нарисовать несколько полосок на листке бумаги. Звучит странно и слишком легко. Когда узнал о нем поподробнее, даже спросил у знакого у Японии:”У вас правда это используют?” и получил одобряющий кивок, я решил сам проверить метод. Он оказался гениальным!

Как это работает: берутся два множителя. Допустим, это будет 16 и 23, как на картинке! Пускай по вертикали будет число 16. Мы берем и разбиваем число на части, как в первом классе нас учат делить слова на слоги. Вверху рисуем одну палочку, отступаем и внизу прорисовываем еще шесть. Таким образом мы изобразили число 16, но палочек всего семь? “Почему?” — спросите вы? Потому что мы разобрали 16 на 1 и 6. Далее по горизонтали прямо на этих линиях рисуем число 23, так же разбиваем его на 2 и 3, только отступаем не вниз, а вправо. И вот, мы видим, как у нас появляются своеобразные решеточки.
Теперь попробуем посчитать. Для начала считаем в левом верхнем углу. При соединении палочек (одной палочки от 16 и двух от 23) образуются точки, как если бы в плюсе + мы выделили серединку точкой, получается что там всего 2 точки. Дальше считаем таким же образом точки в нижнем левом углу и, внимание, в правом верхнем углу. Это число нужно сосчитать вместе! Получается число 15. И теперь считаем точки в правом нижнем углу, там получится 18. Складываем столбиком таким образом: Двойку ставим на первое место в первой строке. Во второй строке пишем 15 так, чтобы единица была под двойкой. И соответственно под числом пять второй строки должно начинаться число 18. Таким образом, восемь — это конец числа, один и пять складываем и получаем 6, и двойку соединяем с единицей. Правильный ответ 368! Проверьте сами, этот способ очень хороший, жаль что с большими числами по типу 99, будет не очень удобно считать.
Основная проблема такого решения — неудобства при счете больших чисел. Не каждый станет рисовать девяносто девять линий на других девяносто девяти. В Японии, когда умножение больших чисел будет необходимо, ученики уже будут знать стандартное умножение в столбик.
Но не все так гладко в японской системе образования. Плюсов у нее достаточно, но и минусы есть: высокая нагрузка на учеников младших классов, сильные требования к умению считать деньги и обращаться с ними. В некоторых школах учат цены в магазинах. Навыки полезные, спорить сложно, но в первом и втором классе. По сравнению с четвертым классом, это еще цветочки. 😀 Множители доходят до тысяч, а то и до миллионов.
Высокие требования не есть плохо, но и не есть хорошо. Стоит понимать, что в японских школах не только математика удосужилась углубленного изучения. Каждый предмет имеет свои специфичные методы, непривычные нам. Но и требования там жестче.Как говорилось в начале статьи, это один из ярких примеров разницы менталитетов.
Мы считаем, что полезное нужно чередовать с приятным. Что и делают наши педагоги на занятиях, давая им учебную и творческую свободы. На них ребенок сразу увидит разницу со школьными уроками: он не просто повторяет школьный курс, но и узнает что-то новое. Кружки и каникулярные программы — приключение в мир математических развлечений. Возможно наша математика и отличается от математики в Японии, но мы считаем, что она ничуть не хуже. 🙂
Летние каникулы все ближе и ближе. Хороший повод изучить, где будут проводиться наши летние программы
Волшебная математика, или Как умножают японцы
Нации, использующие иероглифы, имеют другой тип мышления. Влияет ли это на их жизни? Сложно сказать. Такие люди визуалы по природе, они образно воспринимают окружающий мир. И эта система восприятия не обходит даже точные науки. То, как умножают японцы, будет интересно знать всем. Во-первых, не придется панически искать калькулятор, а во-вторых — это очень увлекательное занятие.
Рисуем
Это удивительно, но японские дети умеют умножать большие числа, даже не зная о таблице умножения. Как умножают японцы? Они делают это очень просто, настолько просто, что используют лишь базовые навыки рисования и счета. Проще показать на примере, как это происходит.
Допустим, необходимо умножить 123 на 321. Для начала нужно нарисовать одну, две и три параллельные линии, которые будут размещаться по диагонали с верхнего левого угла в нижний правый. На созданных группах параллелей нарисовать три, две и одну линию соответственно. Они также будут размещаться по диагонали с нижнего левого угла в правый верхний.
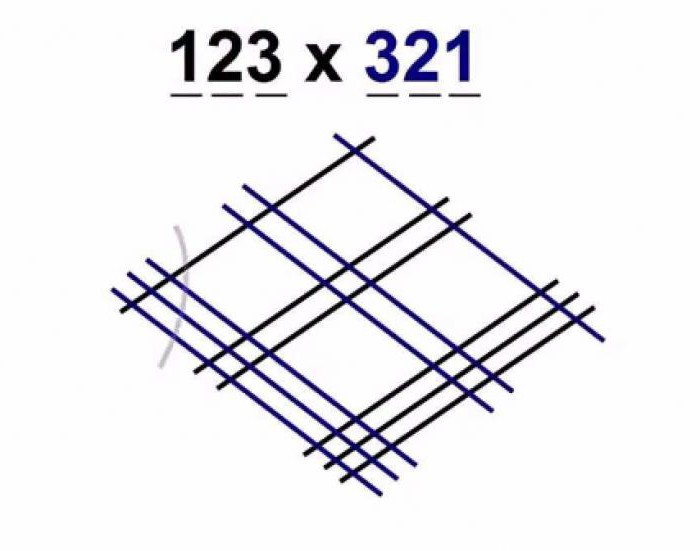
В итоге получим так называемый ромб (как на рисунке выше). Если кто еще не понял, количество линий в группе зависит от чисел, которые нужно перемножить.
Считаем
Итак, как японцы умножают числа? Следующий этап – подсчет точек пересечения. Сначала отделяем полукругом место пересечения трех линий с одной и считаем количество точек. Получившееся число записываем под ромбом. Дальше точно таким же образом отделяем участки, где пересекаются две линии с тремя и одной. Также считаем точки соприкосновения и записываем, потом считаем точки, которые остались в центре. Должен получиться такой результат, как и на рисунке ниже.
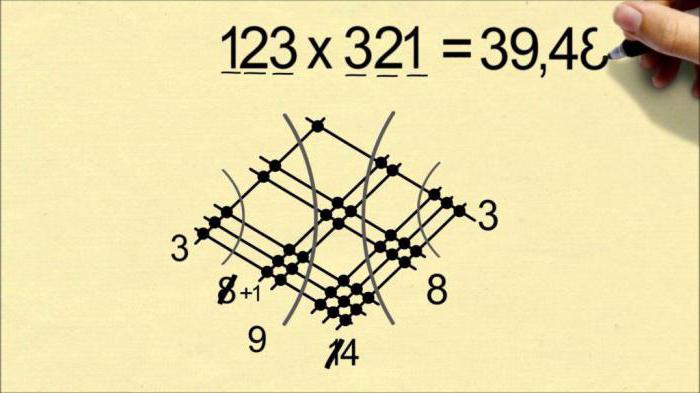
Стоит обратить внимание на то, что если центральное число двузначное, то первую цифру нужно добавить к числу, что получилось при подсчете точек соприкосновения в области слева от центра. Умножив, таким образом, 123 на 321, получим 39 483.
Этим методом можно умножать как двузначные, так и трехзначные числа. Одна проблема в том, что если придется считать такие числа, как 999, 888, 777 и т.д., то нужно будет рисовать очень много черточек.
